Statistical notes for clinical researchers: Type I and type II errors in statistical decision

Hae-Young Kim

doi:10.5395/rde.2015.40.3.249

Articles

Page Path: HOME > Restor Dent Endod > Volume 40(3); 2015 > Article

Open Lecture on Statistics Statistical notes for clinical researchers: Type I and type II errors in statistical decision: Hae-Young Kim; 2015;40(3):-252.
DOI: https://doi.org/10.5395/rde.2015.40.3.249
Published online: June 30, 2015

Department of Health Policy and Management, College of Health Science, and Department of Public Health Sciences, Graduate School, Korea University, Seoul, Korea.

Correspondence to Hae-Young Kim, DDS, PhD. Associate Professor, Department of Health Policy and Management, College of Health Science, and Department of Public Health Sciences, Graduate School, Korea University, 145 Anam-ro, Seongbukgu, Seoul, Korea 136-701. TEL, +82-2-3290-5667; FAX, +82-2-940-2879; kimhaey@korea.ac.kr

©Copyrights 2015. The Korean Academy of Conservative Dentistry.

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

3,523 Views
47 Download
36 Crossref

prev next

Full Article

Download PDF

Null hypothesis and alternative hypothesis
Type I and type II errors
Schematic example of type I and type II errors
Relationship and affecting factors on type I and type II errors
Statistical significance level
Statistical power
REFERENCES

Statistical inference is a procedure that we try to make a decision about a population by using information from a sample which is a part of it. In modern statistics it is assumed that we never know about a population, and there is always a possibility to make errors. Theoretically a sample statistic may have values in a wide range because we may select a variety of different samples, which is called a sampling variation. To get practically meaningful inference we preset a certain level of error. In statistical inference we presume two types of error, type I and type II errors.

Null hypothesis and alternative hypothesis

The first step of statistical testing is the setting of hypotheses. When comparing multiple group means we usually set a null hypothesis. For example, "There is no true mean difference," is a general statement or a default position. The other side is an alternative hypothesis such as "There is a true mean difference." Often the null hypothesis is denoted as H₀ and the alternative hypothesis as H₁ or H_a. To test a hypothesis, we collect data and measure how much the data support or contradict the null hypothesis. If the measured results are similar to or only slightly different from the condition stated by the null hypothesis, we do not reject and accept H₀. However, if the dataset shows a big and significant difference from the condition stated by the null hypothesis, we regard that there is enough evidence that the null hypothesis is not true and reject H₀. When a null hypothesis is rejected, the alternative hypothesis is adopted.

Type I and type II errors

As we assume that we never directly know the information of the population, we never know whether the statistical decision is right or wrong. Actually, the H₀ may be right or wrong and we could make a decision of the acceptance or the rejection of H₀. In a situation of statistical decision, there may be four different occasions as presented in Table 1. Two situations lead correct conclusions that true H₀ is accepted and false H₀ is rejected. However, the others are two incorrect erroneous situations that false H₀ is accepted and true H₀ is rejected. A Type I error or alpha (α) error refers to an erroneous rejection of true H₀. Conversely, a Type II error or beta (β) error refers to an erroneous acceptance of false H₀.

Making some level of error is unavoidable because fundamental uncertainty lies in a statistical inference procedure. As allowing errors is basically harmful, we need to control or limit the maximum level of errors. Which type of error is more risky between type I and type II errors? Traditionally, committing type I error has been considered more risky, and thus more strict control of type I error has been performed in statistical inference.

When we have interest in the null hypothesis only, we may think about type I error only. Let's consider a situation that someone develops a new method and insists that it is more efficient than conventional methods but the new method is actually not more efficient. The truth is H₀ that says "The effects of conventional and newly developed methods are equal." Let's suppose the statistical test results support the efficiency of the new method, which is an erroneous conclusion that the true H₀ is rejected (type I error). According to the conclusion, we consider adopting the newly developed method and making effort to construct a new production system. The erroneous statistical inference with type I error would result in an unnecessary effort and vain investment for nothing better. Otherwise, if the statistical conclusion was made correctly that the conventional and newly developed methods were equal, then we could comfortably stay with the familiar conventional method. Therefore, type I error has been strictly controlled to avoid such useless effort for an inefficient change to adopt new things.

In other example, let's think that we are interested in a safety issue. Someone developed a new method which is actually safer compared to the conventional method. In this situation, null hypothesis states that "Degrees of safety of both methods are equal", when the alternative hypothesis that "The new method is safer than conventional method" is true. Let's suppose that we erroneously accept the null hypothesis (type II error) as the result of statistical inference. We erroneously conclude equal safety and we stay on the less safe conventional environment and have to be exposed to risks continuously. If the risk is a serious one, we would stay in a danger because of the erroneous conclusion with type II error. Therefore, not only type I error but also type II error need to be controlled.

Schematic example of type I and type II errors

Figure 1 shows a schematic example of relative sampling distributions under a null hypothesis (H₀) and an alternative hypothesis (H₁). Let's suppose they are two sampling distributions of sample means (X). H₀ states that sample means are normally distributed with population mean zero. H₁ states the different population mean of 3 under the same shape of sampling distribution. For simplicity, let's assume the standard error of two distributions is one. Therefore, the sampling distribution under H₀ is assumed as the standard normal distribution in this example. In statistical testing on H₀ with an alpha level 0.05, the critical values are set at ± 2 (or exactly 1.96). If the observed sample mean from the dataset lies within ± 2, then we accept H₀, because we don't have enough evidence to deny H₀. Or, if the observed sample mean lies beyond the range, we reject H₀ and adopt H₁. In this example we can say that the probability of alpha error (two-sided) is set at 0.05, because the area beyond ± 2 is 0.05, which is the probability of rejecting the true H₀. As seen in Figure 1, extreme values larger than absolute 2 can appear under H₀ with the standard normal distribution ranging to infinity. However, we practically decide to reject H₀, because the extreme values are too different from the assumed mean, zero. Though the decision includes a probability of error of 0.05, we allow the risk of error because the difference is considered sufficiently big to reach a reasonable conclusion that the null hypothesis is false. As we never know the truth whether the sample dataset we have is from the population H₀ or H₁, we can make decision only based on the value we observe from the sample data.

Type II error is shown as the area lower than 2 under the distribution of H₁. The amount of type II error can be calculated only when the alternative hypothesis suggest a definite value. In Figure 1, a definite mean value of 3 is used in the alternative hypothesis. The critical value 2 is one standard error (= 1) smaller than mean 3 and is standardized to z=-1=2-31

in a standard normal distribution. The area less than z = -1 is 0.16 (yellow area) in standard normal distribution. Therefore, the amount of type II error is obtained as 0.16 in this example.

Relationship and affecting factors on type I and type II errors

1. Related change of both errors

Type I and type II errors are closely related. If all other conditions are the same, the reduction of Type I error level accompanies the increase of type II error level. When we decrease alpha error level from 0.05 to 0.01, the critical value moves outward to around ± 2.58. As the result, beta level will increase to around 0.34 in Figure 1, if all other conditions are the same. Conversely, moving the determinant line to the left side will cause both decrease of type II error level and increase of type I error level. Therefore, the determination of error level should be a procedure considering both error types simultaneously.

2. Effect of distance between H₀ and H₁

If H₁ suggest a bigger center, e.g., 4 instead of 3, then the distribution moves to the right. If we fix the alpha level as 0.05, then the beta level gets smaller than ever. If the center value is 4 then z value is -2 and the area less than -2 in the standard normal distribution is obtained as 0.025. If all other condition is the same, the increase of distance between H₀ and H₁ decrease the beta error level.

3. Effect of sample size

Then how do we maintain both error levels lower? Increasing the sample size is one answer, because a large sample size reduce standard error (standard deviation/√sample size) when all other conditions retained as the same. Smaller standard error can produce more concentrated sampling distributions with slender curve under both null and alternative hypothesis and the consequent overlapping area gets smaller. As sample size increases, we can get satisfactory low levels of both alpha and beta errors.

Statistical significance level

Type I error level of is often called a significance level. In a statistical testing, we reject the null hypothesis when the observed value from the dataset is located in area of extreme 0.05 and conclude there is evidence of difference from the null hypothesis when we set the alpha level at 0.05. As we consider the difference over the level is statistically significant, the level is called a significance level. Sometimes the significance level is expressed using p value, e.g., "Statistical significance was determined as p < 0.05." P value is defined as the probability of obtaining the observed value or more extreme values when the null hypothesis is true. Figure 2 shows that type I error level at 0.05 and a two-sided p value of 0.02. The observed z value 2.3 was located in the rejection region with p value of 0.02, which is smaller than the significance level 0.05. Small p value indicates that the probability of observing such a dataset or more extreme cases is very low under the assumed null hypothesis.

Statistical power

Power is the probability of rejecting a false null hypothesis, which is the other side of type II error. Power is calculated as 1- Type II error (β). In Figure 1, type II error level is 0.16 and power is obtained as 0.84. Usually a power level of 0.8 - 0.9 is required in experimental studies. Because of the relationship between type I and type II errors, we need to keep a minimum required level of both errors. Sufficient sample size is needed to keep the type I error low as 0.05 or 0.01 and the power high as 0.8 or 0.9.

REFERENCES

1. Rosner B. Fundamentals of Biostatistics. 6th ed. Belmont: Duxbury Press; 2006. p. 226-252.

Figure 1

Illustration of type I (α) and type II (β) errors.

Figure 2

Significance level and p value.

Table 1

Possible results of hypothesis testing

Conclusion based on data	Truth
Conclusion based on data	H₀ True	H₀ False
Reject H₀	Type I error (α)	Correct conclusion (Power = 1 - β)
Fail to reject H₀	Correct conclusion (1 - α)	Type II error (β)

Tables & Figures

REFERENCES

Citations

Citations to this article as recorded by

Aquatic Compared With Land‐Based Exercises on Gross Motor Function of Children/Adolescents With Cerebral Palsy: A Systematic Review With Meta‐Analysis
Elton Pauluka, Luize Souto Ceolin, Laís Coan Fontanela, Adriana Neves dos Santos
Child: Care, Health and Development.2025;[Epub] CrossRef
The basic statistical concepts and their interrelationships in diagnostic research
Yitao Mao, Juxiong Xiao, Liping Zhu, Yu Zhang, Yueshuang Leng, Qingling Li, Ying Li, Chuyi Liu, Luqing Zhao
Postgraduate Medical Journal.2025; 101(1193): 263. CrossRef
Basic Statistics for Radiologists: Part 1—Basic Data Interpretation and Inferential Statistics
Adarsh Anil Kumar, Jineesh Valakkada, Anoop Ayyappan, Santhosh Kannath
Indian Journal of Radiology and Imaging.2025; 35(S 01): S58. CrossRef
Quantitative Methodology for Assessing the Quality of Direct Laser Processing of 316L Steel Powder Using Type I and Type II Control Errors
Oleksandr Vasilevskyi, Alexandra Woods, Matthew Jones, Michael Cullinan
Electronics.2025; 14(7): 1476. CrossRef
Platelet Rich Products in Cleft Palate Repair
Samer T. Elsamna, Fayssal Alqudrah, Mahnoor Khan, Teagen Smith, Jon Robitschek, Julia Toman
The Cleft Palate Craniofacial Journal.2025;[Epub] CrossRef
On the effect of flexible adjustment of the p value significance threshold on the reproducibility of randomized clinical trials
Farrokh Habibzadeh, Christine E. King
PLOS One.2025; 20(6): e0325920. CrossRef
Replication, robustness and the angst of false positives: a timely target article and its multifaceted comments
Dan Dediu, Maria Koptjevskaja-Tamm, Kaius Sinnemäki
Linguistic Typology.2025; 29(3): 459. CrossRef
Association between estimated intelligence quotient and treatment outcome in young patients with posttraumatic stress disorder treated with developmentally adapted cognitive processing therapy
Regina Steil, Judith Weiss, Babette Renneberg, Rita Rosner
Cognitive Behaviour Therapy.2025; : 1. CrossRef
Association of climate awareness with urban mobility and consumption behaviour in Accra: a path analysis
Nestor Asiamah, Theophilus Kofi Anyanful, Musah Osumanu Doumbia, Nana Benyi Ansah, Frank Frimpong Opuni, Isaac Aidoo, Faith Muhonja, Simon Mawulorm Agyemang, Cosmos Yarfi, Prince Koranteng Kumi, Kafui Agormeda-Tetteh, Toku Lomatey, Eric Eku
Transportation.2025;[Epub] CrossRef
A quantitative and qualitative assessment of differential privacy’s ability to support collaborative research using a real-world data analysis
David P Gieser, Ashna R Arya, Rebecca Lee Smith, John A Vozenilek, Vishwanath Raman, Jonathan A Handler
JAMIA Open.2025;[Epub] CrossRef
Case study: U.S. airline performance and delay analysis using SAS
Shwadhin Sharma
Journal of Information Technology Teaching Cases.2025;[Epub] CrossRef
Reinterpretation of the results of randomized clinical trials
Farrokh Habibzadeh, Teerapon Dhippayom
PLOS ONE.2024; 19(6): e0305575. CrossRef
Design and validation of a diagnostic suspicion checklist to differentiate epileptic from psychogenic nonepileptic seizures (PNES-DSC)
Pau Sobregrau, Eva Baillès, Joaquim Radua, Mar Carreño, Antonio Donaire, Xavier Setoain, Núria Bargalló, Jordi Rumià, María V. Sánchez Vives, Luis Pintor
Journal of Psychosomatic Research.2024; 180: 111656. CrossRef
CPV Monitoring - Optimization of Control Chart Design by Reducing the False Alarm Rate and Nuisance Signal
Naveenganesh Muralidharan, Thatsinee Johnson, Leyla Rose, Mark Davis
Science Journal of Applied Mathematics and Statistics.2024; 12(2): 20. CrossRef
Risk Factors and Dynamic Nomogram Development for Surgical Site Infection Following Open Wedge High Tibial Osteotomy for Varus Knee Osteoarthritis: A Retrospective Cohort Study
Haichuan Guo, Bixuan Song, Ruijuan Zhou, Jiahao Yu, Pengzhao Chen, Bin Yang, Naihao Pan, Chengsi Li, Yanbin Zhu, Juan Wang
Clinical Interventions in Aging.2023; Volume 18: 2141. CrossRef
Psychiatric and psychological assessment of Spanish patients with drug-resistant epilepsy and psychogenic nonepileptic seizures (PNES) with no response to previous treatments
Pau Sobregrau, Eva Baillès, Mar Carreño, Antonio Donaire, Teresa Boget, Xavier Setoain, Núria Bargalló, Jordi Rumià, María V Sánchez Vives, Luís Pintor
Epilepsy & Behavior.2023; 145: 109329. CrossRef
Cold Water Immersion Directly and Mediated by Alleviated Pain to Promote Quality of Life in Indonesian with Gout Arthritis: A Community-based Randomized Controlled Trial
Maria Dyah Kurniasari, Karen A. Monsen, Shuen Fu Weng, Chyn Yng Yang, Hsiu Ting Tsai
Biological Research For Nursing.2022; 24(2): 245. CrossRef
The impact of COVID-19 infection on hip fracture 30-day mortality
Ahmed Fadulelmola, Rob Gregory, Gavin Gordon, Fiona Smith, Andrew Jennings
Trauma.2022; 24(2): 109. CrossRef
Adjuvant radiation vs Chemoradiation in HPV+ oropharyngeal squamous cell carcinoma with extranodal extension
Samer T. Elsamna, Ghayoour S. Mir, Ibraheem Shaikh, Rohan Shah, Soly Baredes, Richard Chan Woo Park, Dylan F. Roden
Oral Oncology Reports.2022; 1-2: 100003. CrossRef
Improving Student Attitudes and Academic Performance in Introductory Biology Using a Project-Based Learning Community
Tyesha N. Burks
Journal of Microbiology & Biology Education.2022;[Epub] CrossRef
Algorithm for sample availability prediction in a hospital-based epidemiological study spreadsheet-based sample availability calculator
Amrit Sudershan, Kanak Mahajan, Rakesh K. Panjaliya, Manoj K. Dhar, Parvinder Kumar
Scientific Reports.2022;[Epub] CrossRef
Psychiatric and Psychosocial Characteristics of a Cohort of Spanish Individuals Attending Genetic Counseling Due to Risk for Genetically Conditioned Dementia
Pau Sobregrau, Josep M. Peri, Raquel Sánchez del Valle, Jose L. Molinuevo, Bernardo Barra, Luís Pintor
Journal of Alzheimer's Disease Reports.2022; 6(1): 461. CrossRef
Interactions in the 2×2×2 factorial randomised clinical STEPCARE trial and the potential effects on conclusions: a protocol for a simulation study
Markus Harboe Olsen, Aksel Karl Georg Jensen, Josef Dankiewicz, Markus B. Skrifvars, Matti Reinikainen, Marjaana Tiainen, Manoj Saxena, Anders Aneman, Christian Gluud, Susann Ullén, Niklas Nielsen, Janus Christian Jakobsen
Trials.2022;[Epub] CrossRef
Test Corrections Appear To Benefit Lower-Achieving Students in an Introduction to Biology Major Course: Results of a Single-Site, One-Semester Study
Kyeorda Kemp
Journal of Microbiology & Biology Education.2021;[Epub] CrossRef
The impact of COVID-19 infection on hip fractures 30-day mortality
Ahmed Fadulelmola, Rob Gregory, Gavin Gordon, Fiona Smith, Andrew Jennings
Trauma.2021; 23(4): 295. CrossRef
The effectiveness of the role of advanced nurse practitioners compared to physician-led or usual care: A systematic review
Maung Htay, Dean Whitehead
International Journal of Nursing Studies Advances.2021; 3: 100034. CrossRef
p-Hacking as a Questionable Research Practice in Industrial and Organizational Psychology
Bogdan Cocoș
Studia Doctoralia.2021; 12(1): 1. CrossRef
Gene–environment interaction: Oxytocin receptor (OXTR) polymorphisms and parenting style as potential predictors for depressive symptoms
Rebecka Keijser, Cecilia Åslund, Kent W. Nilsson, Susanne Olofsdotter
Psychiatry Research.2021; 303: 114057. CrossRef
Heart failure development in obesity: underlying risk factors and mechanistic pathways
Shabbar Jamaly, Lena Carlsson, Markku Peltonen, Johanna C. Andersson‐Assarsson, Kristjan Karason
ESC Heart Failure.2021; 8(1): 356. CrossRef
Mapping social reward and punishment processing in the human brain: A voxel-based meta-analysis of neuroimaging findings using the social incentive delay task
D. Martins, L. Rademacher, A.S. Gabay, R. Taylor, J.A. Richey, D.V. Smith, K.S. Goerlich, L. Nawijn, H.R. Cremers, R. Wilson, S. Bhattacharyya, Y. Paloyelis
Neuroscience & Biobehavioral Reviews.2021; 122: 1. CrossRef
Experts’ perceptions on the use of visual analytics for complex mental healthcare planning: an exploratory study
Erin I. Walsh, Younjin Chung, Nicolas Cherbuin, Luis Salvador-Carulla
BMC Medical Research Methodology.2020;[Epub] CrossRef
Flexible Data Trimming Improves Performance of Global Machine Learning Methods in Omics-Based Personalized Oncology
Victor Tkachev, Maxim Sorokin, Constantin Borisov, Andrew Garazha, Anton Buzdin, Nicolas Borisov
International Journal of Molecular Sciences.2020; 21(3): 713. CrossRef
Phthalates exposure and attention-deficit/hyperactivity disorder in children: a systematic review of epidemiological literature
Sarva Mangala Praveena, Rusheni Munisvaradass, Ruziana Masiran, Ranjith Kumar Rajendran, Chu-Ching Lin, Suresh Kumar
Environmental Science and Pollution Research.2020; 27(36): 44757. CrossRef
ThicknessTool: automated ImageJ retinal layer thickness and profile in digital images
Daniel E. Maidana, Shoji Notomi, Takashi Ueta, Tianna Zhou, Danica Joseph, Cassandra Kosmidou, Josep Maria Caminal-Mitjana, Joan W. Miller, Demetrios G. Vavvas
Scientific Reports.2020;[Epub] CrossRef
Predictors of Flu Vaccination for Persons Living With HIV in Central Texas
Julie A. Zuñiga, Alexandra A. García, Jonathan Fordyce, Ya-Ching Huang, Jungmin Park, Jane D. Champion
Journal of the Association of Nurses in AIDS Care.2019; 30(5): 593. CrossRef
Type I, II, and III statistical errors: A brief overview
Parampreet Kaur, Jill Stoltzfus
International Journal of Academic Medicine.2017; 3(2): 268. CrossRef

ePub Link

Cite

CITE: export Copy Download Format; Close

Download Citation

Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.

Format:

RIS — For EndNote, ProCite, RefWorks, and most other reference management software
BibTeX — For JabRef, BibDesk, and other BibTeX-specific software

Include:

Citation for the content below
Citation and abstract for the content below

Statistical notes for clinical researchers: Type I and type II errors in statistical decision

Restor Dent Endod. 2015;40(3):249-252. Published online June 30, 2015

DOI: https://doi.org/10.5395/rde.2015.40.3.249

XML Download

Figure

Statistical notes for clinical researchers: Type I and type II errors in statistical decision

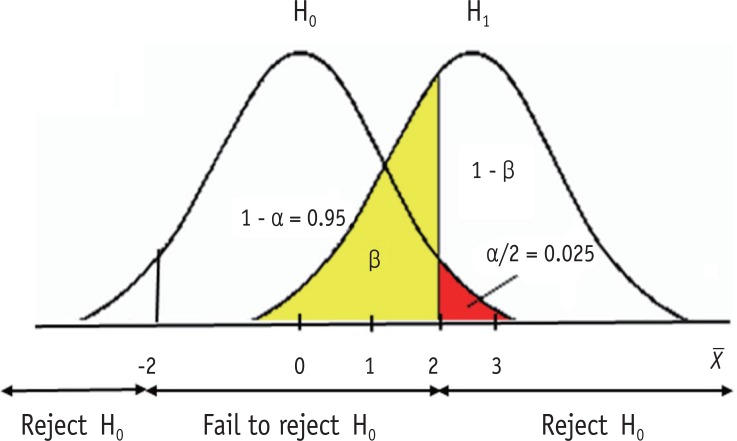
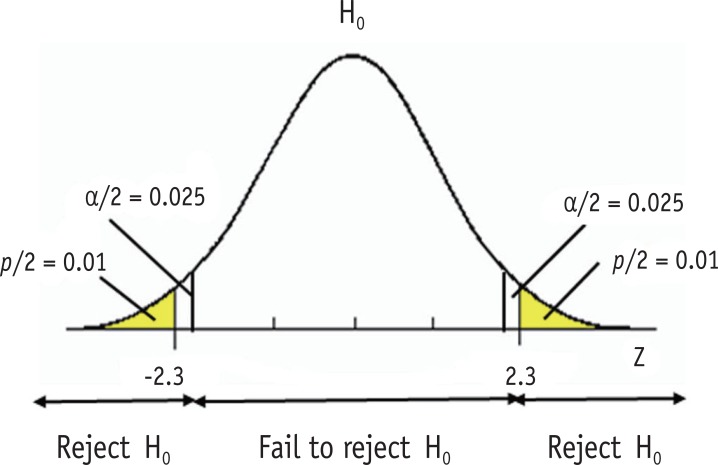
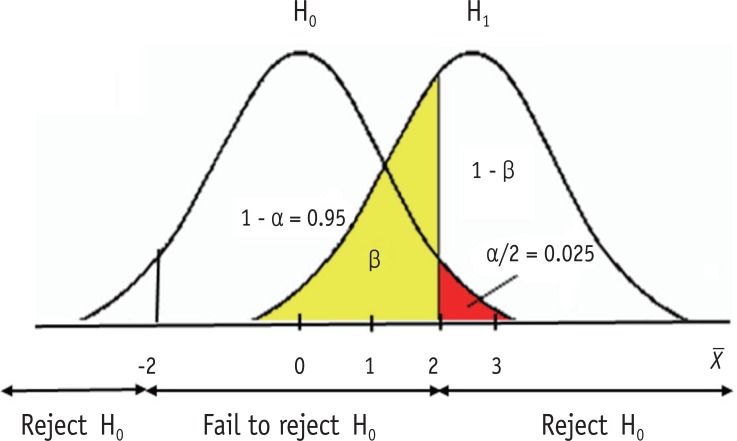
Figure 1 Illustration of type I (α) and type II (β) errors.

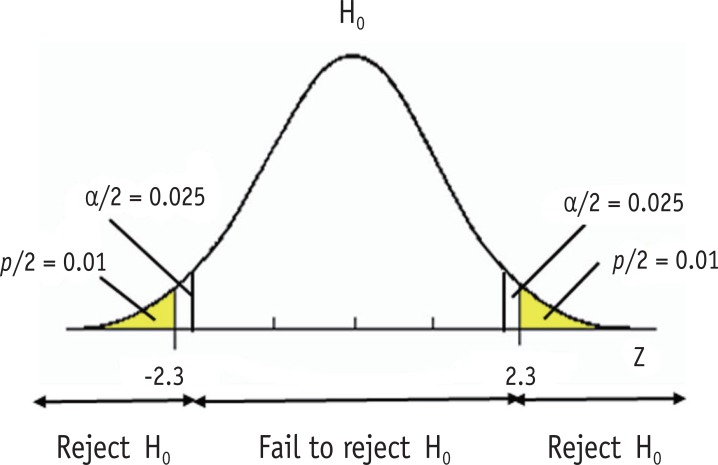
Figure 2 Significance level and p value.

Figure 1

Figure 2

Statistical notes for clinical researchers: Type I and type II errors in statistical decision

Table 1

Possible results of hypothesis testing

Conclusion based on data	Truth
Conclusion based on data	H₀ True	H₀ False
Reject H₀	Type I error (α)	Correct conclusion (Power = 1 - β)
Fail to reject H₀	Correct conclusion (1 - α)	Type II error (β)

Table 1 Possible results of hypothesis testing