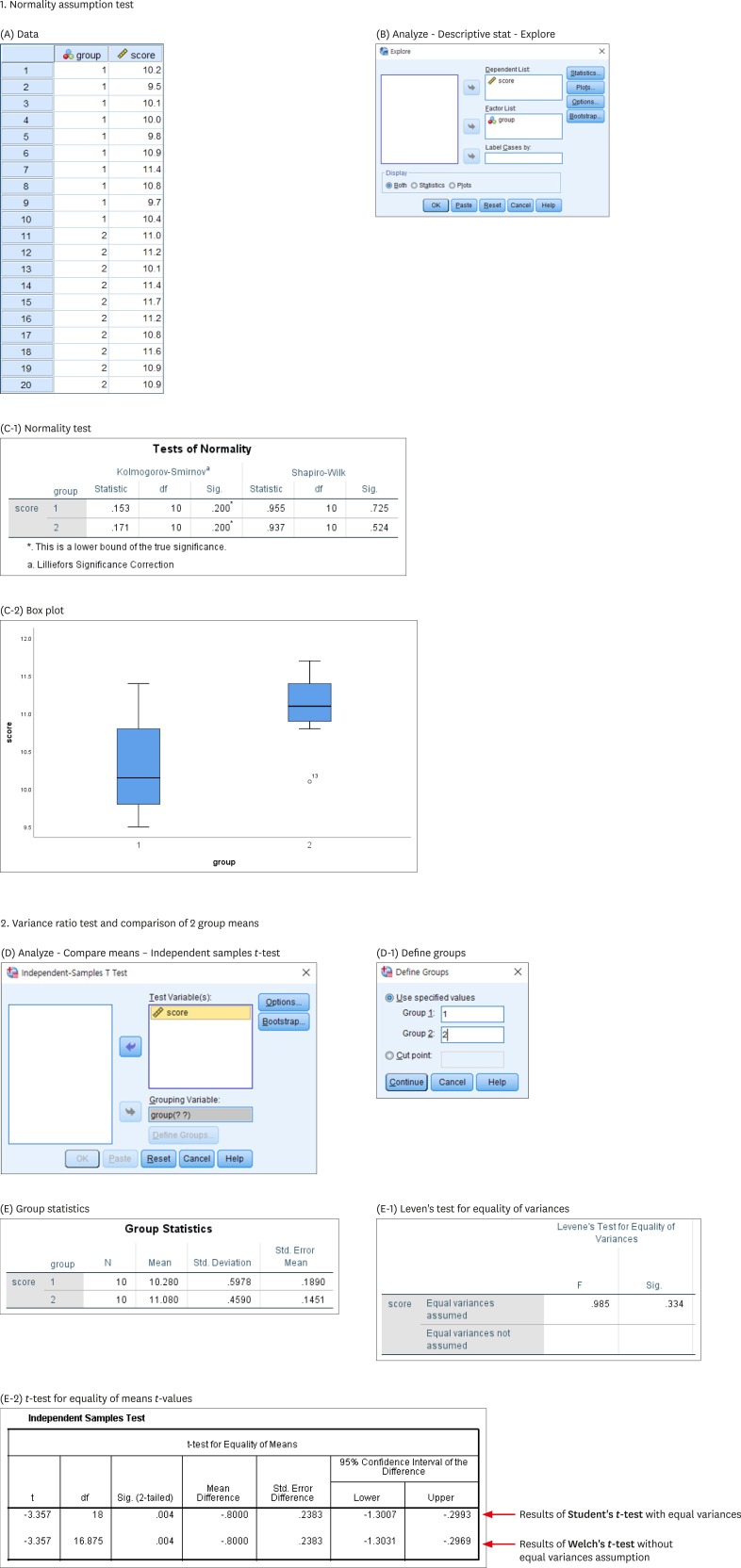
Articles
- Page Path
- HOME > Restor Dent Endod > Volume 44(3); 2019 > Article
-
Open Lecture on Statistics
Statistical notes for clinical researchers: the independent samples
t -test -
Hae-Young Kim

-
Restor Dent Endod 2019;44(3):e26.
DOI: https://doi.org/10.5395/rde.2019.44.e26
Published online: July 17, 2019
Department of Health Policy and Management, College of Health Science, andDepartment of Public Health Science, Graduate School, Korea University, Seoul,Korea.
- Correspondence to Hae-Young Kim, DDS, PhD. Professor, Department of Health Policy and Management, Korea University College of Health Science, and Department of Public Health Science, Korea University Graduate School, 145 Anam-ro, Seongbuk-gu, Seoul 02841, Korea. kimhaey@korea.ac.kr
Copyright © 2019. The Korean Academy of Conservative Dentistry
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
- 10,243 Views
- 227 Download
- 55 Crossref
The t-test is frequently used in comparing 2 group means. The compared
groups may be independent to each other such as men and women. Otherwise, compared data
are correlated in a case such as comparison of blood pressure levels from the same
person before and after medication (Figure 1). In
this section we will focus on independent t-test only. There are 2
kinds of independent t-test depending on whether 2 group variances can
be assumed equal or not. The t-test is based on the inference using
t-distribution.
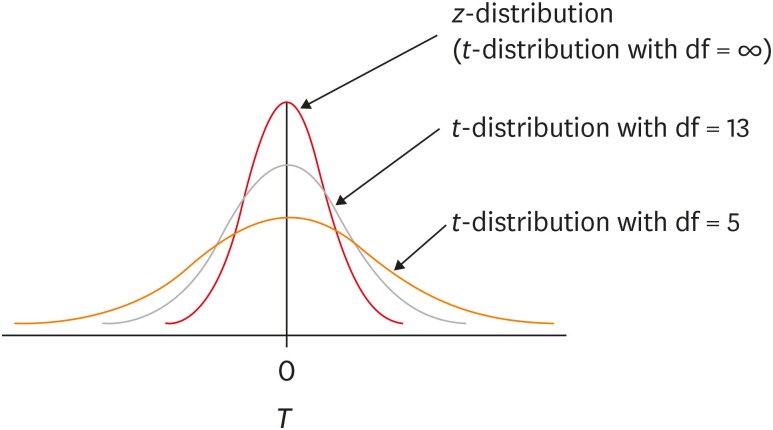
T-DISTRIBUTION
The t-distribution was invented in 1908 by William Sealy Gosset, who
was working for the Guinness brewery in Dublin, Ireland. As the Guinness brewery did
not permit their employee's publishing the research results related to their work,
Gosset published his findings by a pseudonym, “Student.” Therefore,
the distribution he suggested was called as Student's
t-distribution. The t-distribution is a
distribution similar to the standard normal distribution,
z-distribution, but has lower peak and higher tail compared to it
(Figure 2).
According to the sampling theory, when samples are drawn from a normal-distributed
population, the distribution of sample means is expected to be a normal
distribution. When we know the variance of population, σ2, we can
define the distribution of sample means as a normal distribution and adopt
z-distribution in statistical inference. However, in reality,
we generally never know σ2, we use sample variance,
s2, instead. Although the
s2 is the best estimator for σ2,
the degree of accuracy of s2 depends on the sample size.
When the sample size is large enough (e.g., n =
300), we expect that the sample variance would be very similar to the population
variance. However, when sample size is small, such as n = 10, we
could guess that the accuracy of sample variance may be not that high. The
t-distribution reflects this difference of uncertainty
according to sample size. Therefore the shape of t-distribution
changes by the degree of freedom (df), which is sample size minus one (n − 1)
when one sample mean is tested.
The t-distribution appears to be a family of distribution of which
shape varies according to its df (Figure 2).
When df is smaller, the t-distribution has lower peak and higher
tail compared to those with higher df. The shape of t-distribution
approaches to z-distribution as df increases. When df gets large
enough, e.g., n = 300,
t-distribution is almost identical with
z-distribution. For the inferences of means using small samples, it
is necessary to apply t-distribution, while similar inference can
be obtain by either t-distribution or
z-distribution for a case with a large sample. For inference of 2
means, we generally use t-test based on
t-distribution regardless of the sizes of sample because it is
always safe, not only for a test with small df but also for that with large df.
INDEPENDENT SAMPLES T-TEST
To adopt z- or t-distribution for inference using
small samples, a basic assumption is that the distribution of population is not
significantly different from normal distribution. As seen in Appendix 1, the normality assumption needs to be tested in
advance. If normality assumption cannot be met and we have a small sample
(n < 25), then we are not permitted to use
‘parametric’ t-test. Instead, a non-parametric
analysis such as Mann-Whitney U test should be selected.
For comparison of 2 independent group means, we can use a
z-statistic to test the hypothesis of equal population means only
if we know the population variances of 2 groups, σ 1 2 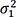 and
and σ 2 2 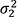 , as follows;
, as follows;
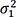 and
and 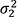 , as follows;
, as follows;where X̄1 and
X̄2, σ 1 2 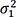 and
and σ 2 2 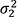 , and n1 and
n2 are sample means, population variances, and the
sizes of 2 groups.
, and n1 and
n2 are sample means, population variances, and the
sizes of 2 groups.
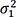 and
and 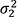 , and n1 and
n2 are sample means, population variances, and the
sizes of 2 groups.
, and n1 and
n2 are sample means, population variances, and the
sizes of 2 groups.Again, as we never know the population variances, we need to use sample variances as
their estimates. There are 2 methods whether 2 population variances could be assumed
equal or not. Under assumption of equal variances, the t-test
devised by Gosset in 1908, Student's t-test, can be applied. The
other version is Welch's t-test introduced in 1947, for the cases
where the assumption of equal variances cannot be accepted because quite a big
difference is observed between 2 sample variances.
In Student's t-test, the population variances are assumed equal.
Therefore, we need only one common variance estimate for 2 groups. The common
variance estimate is calculated as a pooled variance, a weighted average of 2
sample variances as follows;
where s 1 2 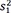 and
and s 2 2 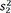 are sample variances.
are sample variances.
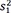 and
and 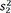 are sample variances.
are sample variances.The resulting t-test statistic is a form that both the
population variances, σ 1 2 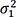 and
and σ 1 2 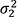 , are exchanged with a common variance
estimate,
, are exchanged with a common variance
estimate, s p 2 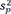 . The df is given as
n1 + n2 − 2
for the t-test statistic.
. The df is given as
n1 + n2 − 2
for the t-test statistic.
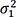 and
and 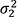 , are exchanged with a common variance
estimate,
, are exchanged with a common variance
estimate, 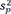 . The df is given as
n1 + n2 − 2
for the t-test statistic.
. The df is given as
n1 + n2 − 2
for the t-test statistic.In Appendix 1, ‘(E-1) Leven's test
for equality of variances’ shows that the null hypothesis of equal
variances was accepted by the high p value, 0.334 (under
heading of Sig.). In ‘(E-2) t-test for equality of means
t-values’, the upper line shows the result of
Student's t-test. The t-value and df are shown
−3.357 and 18. We can get the same figures using the formulas Eq. 2 and
Eq. 3, and descriptive statistics in Table
1, as follows.
The result of calculation is a little different from that by SPSS (IBM Corp.,
Armonk, NY, USA) of Appendix 1, maybe
because of rounding errors.
Actually there are a lot of cases where the equal variance cannot be assumed.
Even if it is unlikely to assume equal variances, we still compare 2 independent
group means by performing the Welch's t-test. Welch's
t-test is more reliable when the 2 samples have unequal
variances and/or unequal sample sizes. We need to maintain the assumption of
normality.
Because the population variances are not equal, we have to estimate them
separately by 2 sample variances, s 1 2 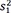 and
and s 2 2 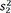 . As the result, the form of
t-test statistic is given as follows;
. As the result, the form of
t-test statistic is given as follows;
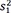 and
and 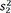 . As the result, the form of
t-test statistic is given as follows;
. As the result, the form of
t-test statistic is given as follows;where ν is Satterthwaite degrees of freedom.
In Appendix 1, ‘(E-1) Leven's test
for equality of variances’ shows an equal variance can be successfully
assumed (p = 0.334). Therefore, the Welch's
t-test is inappropriate for this data. Only for the purpose of
exercise, we can try to interpret the results of Welch's t-test
shown in the lower line in ‘(E-2) t-test for equality of
means t-values’. The t-value and df are
shown as −3.357 and 16.875.
We've confirmed nearly same results by calculation using the formula and by SPSS
software.
The t-test is one of frequently used analysis methods for
comparing 2 group means. However, sometimes we forget the underlying assumptions
such as normality assumption or miss the meaning of equal variance assumption.
Especially when we have a small sample, we need to check normality assumption
first and make a decision between the parametric t-test and the
nonparametric Mann-Whitney U test. Also, we need to assess the
assumption of equal variances and select either Student's
t-test or Welch's t-test.
Appendix
Tables & Figures
REFERENCES
Citations
Citations to this article as recorded by 

- Examining Gender Differences in Aggression as a Predictor of Anxiety, Depression, and Suicide in a Cross‐Sectional French Sample
Sylvia Martin
Health Science Reports.2025;[Epub] CrossRef - Structural and topological analysis of thiosemicarbazone-based metal complexes: computational and experimental study of bacterial biofilm inhibition and antioxidant activity
Doaa S. El‑Sayed, Shaymaa S. Hassan, Liblab S. Jassim, Ali Abdullah Issa, Firas AL-Oqaili, Mustafa k. Albayaty, Buthenia A. Hasoon, Majid S. Jabir, Khetam H. Rasool, Hemmat A. Elbadawy
BMC Chemistry.2025;[Epub] CrossRef - xeredar: An open-source R package for the statistical analysis of endocrine new approach methodologies using fish and amphibian eleutheroembryos
Inka Marie Spyridonov, Lijuan Yan, Eduard Szöcs, Ana Filipa Pereira Miranda, Carsten Lange, Andrew Tindall, David Du Pasquier, Gregory Lemkine, Lennart Weltje, Maike Habekost, Pernille Thorbek
Environmental Toxicology and Chemistry.2025; 44(9): 2673. CrossRef - Dealing with lipoedema: women’s experiences of healthcare, self-care, and treatments—a mixed-methods study
Johanna Falck, Annette Nygårdh, Bo Rolander, Lise-Lotte Jonasson, Jan Mårtensson
BMC Women's Health.2025;[Epub] CrossRef - Learning From Principals: Exploring Malaysian Primary Deputy Principals’ Informal Mentoring Experiences
Lokman Mohd Tahir, Roslizam Hassan, Mohammed Borhandden Musah
SAGE Open.2025;[Epub] CrossRef - Transcriptomic studies on the product stress response revealed that YCF1 is a beneficial factor for progesterone production in Yarrowia lipolytica
Ying Wang, Ruosi Zhang, Mingdong Yao, Wenhai Xiao, Ying Wang, Ying-Jin Yuan
Synthetic and Systems Biotechnology.2025; 10(4): 1087. CrossRef - Remote Monitoring of Psoriasis: Comparing Care Models and Evaluating Quality of Life Outcomes: Mixed Methods Study
Jana Arsenjeva, Priit Kruus, Riina Hallik, Secil Matasova, Laura Prett, Katrin Kaarna, Liisi Raam, Oliver Taul, Liis Ilves, Kaisa Viljar, Pille Konno, Peeter Ross, Külli Kingo
Journal of Medical Internet Research.2025; 27: e73664. CrossRef - Preoperative lower limb kinematic analysis in spinal sagittal imbalance using machine learning and IMU sensors
Sadegh Madadi, Mostafa Rostami, Hadi Farahani, Farshad Nikouee, Mohammad Samadian, Ram Haddas
Signal, Image and Video Processing.2025;[Epub] CrossRef - Predictive for patients with pneumonia in pediatric intensive care unit
Mingxuan Jia, Xiyan Hu, Lin Ji, Jiawen Lin, Jialin Liu, Yong Wang
Frontiers in Pediatrics.2025;[Epub] CrossRef - Enjoyment, Empathy, and Environmental Behavior: A Study of Young Children’s Nature Connection in Iceland
Meghan C. Orman, Shannon B. Wanless, Freyja Birgisdóttir, Kristín Norðdahl
Journal of Cognition and Development.2025; : 1. CrossRef - Source discrimination of colchicine based on carbon stable isotope analysis
Hanyang Zheng, Jun Zhu, Zhuotong Cai, Zhaowei Jie, Wei Wang, Hanyu Zhang, Can Hu, Hongling Guo, Hongcheng Mei
Journal of Forensic Sciences.2025; 70(6): 2227. CrossRef - Empirical Investigation of the Motivation and Perceptions of Tourists Visiting Spa Resorts in the Vâlcea Subcarpathians, Romania
Amalia Niță, Ionuț-Adrian Drăguleasa
Sustainability.2025; 17(14): 6590. CrossRef - Barriers and drivers of digitalization of technical products: a survey in industry
Michel Fett, Richard Breimann, Adrian Mustafa, Angelina Hirsch, Chentao Cai, Matthias Striebel, Jonathan Dagnew, Eckhard Kirchner
Forschung im Ingenieurwesen.2025;[Epub] CrossRef - Late secondary alveolar bone grafting using autologous versus alloplastic material for treating patients with cleft lip and palate with one year follow-up—A retrospective comparative study
Amrit Thapa, Saugat Ray, B. Jayan, S.S. Chopra, B.S. Walia, Abhijeet Kadu, Kapil Tomar
Journal of Plastic, Reconstructive & Aesthetic Surgery.2025; 110: 35. CrossRef - Las inyecciones de plasma rico en plaquetas mejoran los resultados funcionales en comparación con la radiofrecuencia pulsada mediante bloqueo del ganglio impar en el tratamiento de la coxigodinia
J. Pilco Inga, A. Fervienza Sánchez, J.J. Velázquez Fragoso, M. Fa-Binefa, I. Moya Molinas
Revista Española de Anestesiología y Reanimación.2025; 72(10): 501929. CrossRef - The Role of Character Strengths in Employment Among People With Multiple Sclerosis
Beatrice Lee
Rehabilitation Counseling Bulletin.2025;[Epub] CrossRef - Students’ attitudes toward LLMs and its association with metacognitive abilities: A cross-sectional study
Shihui Natalie Yeh, Chiew-Jiat Rosalind Siah
Nurse Education in Practice.2025; 88: 104567. CrossRef - Preparing for the Future: Evaluating the Employability Skills of 4-H Extension Agents
William Norris, Adebayo Adeoti, Jake Devine
Journal of Agricultural Education.2025; 66(4): 4. CrossRef - Platelet-rich plasma injections improve functional results over pulsed radiofrequency in ganglion impar treatments for coccydynia
J. Pilco Inga, A. Fervienza Sánchez, J.J. Velázquez Fragoso, M. Fa-Binefa, I. Moya Molinas
Revista Española de Anestesiología y Reanimación (English Edition).2025; 72(10): 501929. CrossRef - Network architecture optimization for ophthalmic ultrasound image detection based on modular ablation of multi-version YOLO
Zemeng Li, Xiaochun Wang, Xinqi Yu, Zhiyuan Zhao, Yan Wang, Sheng Zhou
BioMedical Engineering OnLine.2025;[Epub] CrossRef - Delays in diagnosis and treatment of lymphoma in Nepal: A cross-sectional study
Jasmine Gurung, Bishesh S Poudyal, Bishnu D Poudel, Bibek Acharya, Sandhya Chapagain, Saugat Poudyal, Pradeep Thapa, Shama Pandey, Ramila Shilpakar
Cancer Research, Statistics, and Treatment.2025; 8(4): 269. CrossRef - THE RELATIONSHIP BETWEEN FINANCIAL BEHAVIOR AND DETERMINANTS OF FINANCIAL EDUCATION DEMAND: AN APPLICATION TO UNIVERSITY STUDENTS
Kutlu Ergün
Uluslararası İktisadi ve İdari İncelemeler Dergisi.2025; (49): 429. CrossRef - Genome-Wide Identification, Characterization, and Expression Profiles of TLR Genes in Darkbarbel Catfish (Pelteobagrus vachelli) Following Aeromonas hydrophila Infection
Zhengyong Wen, Lisha Guo, Jianchao Chen, Qiyu Chen, Yanping Li, Yunyun Lv, Qiong Shi, Shengtao Guo
Biology.2025; 14(12): 1724. CrossRef - Assessing the contribution of impoundment–induced climate change to vegetation growth in the Xiluodu reservoir area of the Jinsha River
Xinyan Wu, Meng Hao, Jingya Wen, Pengyuan Wang, Chenxu Ji, Yong Huang
Ecological Frontiers.2025;[Epub] CrossRef - Comparison of the effects of video conference and video-based home exercise on physical performance and body composition in older adult individuals
Özgün Elmas, Mustafa Cemali, Ayşe Livanelioğlu
Medicine.2024; 103(44): e40329. CrossRef - Deep Residual Learning-Based Classification with Identification of Incorrect Predictions and Quantification of Cellularity and Nuclear Morphological Features in Digital Pathological Images of Common Astrocytic Tumors
Yen-Chang Chen, Shinn-Zong Lin, Jia-Ru Wu, Wei-Hsiang Yu, Horng-Jyh Harn, Wen-Chiuan Tsai, Ching-Ann Liu, Ken-Leiang Kuo, Chao-Yuan Yeh, Sheng-Tzung Tsai
Cancers.2024; 16(13): 2449. CrossRef - The Impact of Stress First Aid on Perceived Stress Levels of New Graduate Nurses
John R. Balcuk
Nursing Economic$.2024; 42(4): 191. CrossRef - CloudBrain-MRS: An intelligent cloud computing platform for in vivo magnetic resonance spectroscopy preprocessing, quantification, and analysis
Xiaodie Chen, Jiayu Li, Dicheng Chen, Yirong Zhou, Zhangren Tu, Meijin Lin, Taishan Kang, Jianzhong Lin, Tao Gong, Liuhong Zhu, Jianjun Zhou, Ou-yang Lin, Jiefeng Guo, Jiyang Dong, Di Guo, Xiaobo Qu
Journal of Magnetic Resonance.2024; 358: 107601. CrossRef - Bactericidal activities and biochemical features of 16 antimicrobial peptides against bovine-mastitis causative pathogens
Hye-sun Cho, Dohun Kim, Hyoim Jeon, Prathap Somasundaram, Nagasundarapandian Soundrarajan, Chankyu Park
Veterinary Research.2024;[Epub] CrossRef - Expressions of Interleukin-4 and Interleukin-5 in Nodular Prurigo and Pruritic Papular Lesions
Ayu Wikan Sayekti, Ann Kautsaria Putri, Dwi Retno Adi Winarni, Satiti Retno Pudjiati
Folia Medica Indonesiana.2024; 60(1): 47. CrossRef - Challenges and barriers to e-leadership participation: Examining the perspectives of Malaysian secondary school teachers
Cha Shi Ping, Lokman Mohd Tahir, Mohd Shafie Rosli, Noor Azean Atan, Mohd Fadzli Ali
Education and Information Technologies.2024; 29(8): 10329. CrossRef - One-Leg Standing Test with Eyes Open as a Screening Tool for Prefrailty in Community-Dwelling Older Japanese Women
Zhenyue Liu, Shuji Sawada, Hisashi Naito, Shuichi Machida
Healthcare.2024; 12(23): 2378. CrossRef - Detection of cardiovascular disease cases using advanced tree-based machine learning algorithms
Fariba Asadi, Reza Homayounfar, Yaser Mehrali, Chiara Masci, Samaneh Talebi, Farid Zayeri
Scientific Reports.2024;[Epub] CrossRef - Recent Advancements in Subcellular Proteomics: Growing Impact of Organellar Protein Niches on the Understanding of Cell Biology
Vanya Bhushan, Aleksandra Nita-Lazar
Journal of Proteome Research.2024; 23(8): 2700. CrossRef - A comparison study: The use of digital and conventional impression techniques in dental hygiene education
Raha K. Naderi, Tulsi J. Patel, Michelle A. Thompson
Journal of Dental Education.2024; 88(5): 518. CrossRef - An Evaluation of the Nunez Community College Quality Enhancement Program: Assessing the Impact of Embedded Conover Workplace Readiness® Modules on Students’ Work Readiness
Sandra Aurand Bosch, Donna Mowery Rice
Sage Open.2024;[Epub] CrossRef - Integrating electric vehicles into hybrid microgrids: A stochastic approach to future-ready renewable energy solutions and management
Aykut Fatih Güven
Energy.2024; 303: 131968. CrossRef - Comparison of postural assessment and awareness in individuals receiving posture training using the digital AI posture assessment and correction system
Musa Çankaya, Fatma Nur Takı
International Journal of Occupational Safety and Ergonomics.2024; 30(4): 1311. CrossRef - Detection and Analysis of Fake News Users’ Communities in Social Media
Abdelouahab Amira, Abdelouahid Derhab, Samir Hadjar, Mustapha Merazka, Md. Golam Rabiul Alam, Mohammad Mehedi Hassan
IEEE Transactions on Computational Social Systems.2024; 11(4): 5050. CrossRef - How do fish miss? Attack strategies of threespine stickleback capturing non-evasive prey
Seth Shirazi, Timothy E. Higham
Journal of Experimental Biology.2024;[Epub] CrossRef - Effects of Occlusal Contact on Maxillary Alveolar Bone Morphology in Patients with and without Anterior Open Bite: A Cross-Sectional Study
Chiyo Shimizu-Tomoda, Yuji Ishida, Aiko Ishizaki-Terauchi, Yukari Mizoguchi, Shuji Oishi, Takashi Ono
Journal of Clinical Medicine.2024; 13(11): 3061. CrossRef - Bioceramic modular tissue-engineered bone with rapid vascularization for large bone defects
Siwei Luo, Zhen Wang, Jialin He, Geng Tang, Daizhu Yuan, Zhanyu Wu, Zihao Zou, Long Yang, Tao Lu, Chuan Ye
Ceramics International.2024; 50(11): 18275. CrossRef - Effect of Arogya Raksha Panchatantra (five lifestyle principles) on heart rate variability, menstrual symptoms, health-related quality of life, performance and self-efficacy in Young female adults with primary dysmenorrhea: protocol for an exploratory ran
Karishma Silwal, Prakash Babu Kodali, Vakeel Khan, Hemanshu Sharma, Gulab Rai Tewani, Pradeep M. K. Nair
CCRYN Indian Journal of Yoga & Naturopathy.2024; 1(1): 15. CrossRef - Letter to the editor on: “Calcaneal positioning in equinus immobilization of the ankle joint: A comparison of common orthoses used in the treatment of acute Achilles tendon ruptures”
Rahul Kumar, Diggaj Shrestha, Kunal Setia, Sunita Sharma
Foot and Ankle Surgery.2023; 29(6): 498. CrossRef - Irradiation damage reduces alloy corrosion rate via oxide space charge compensation effects
Zefeng Yu, Elizabeth Kautz, Hongliang Zhang, Anton Schneider, Taeho Kim, Yongfeng Zhang, Sten Lambeets, Arun Devaraj, Adrien Couet
Acta Materialia.2023; 253: 118956. CrossRef - Predictors of Relevant Changes in Pain and Function for Adolescents With Idiopathic Scoliosis Following Surgery
Samia Alamrani, Adrian Gardner, Alison B. Rushton, Deborah Falla, Nicola R. Heneghan
Spine.2023; 48(16): 1166. CrossRef - A multicenter feasibility study on implementing a brief mindful breathing exercise into regular university courses
Annika C. Konrad, Veronika Engert, Reyk Albrecht, Christian Dobel, Nicola Döring, Jens Haueisen, Olga Klimecki, Mike Sandbothe, Philipp Kanske
Scientific Reports.2023;[Epub] CrossRef - Adult children of parents with mental illness: Family stigma and coping on sense of self
Chynna Campbell, Pamela Patrick
Child & Family Social Work.2023; 28(3): 622. CrossRef - Veri Madenciliğine Dayalı Olarak Çalışanların Örgütsel Bağlılık Düzeyinin Belirlenmesi: İstanbul ve Kocaeli Örneği
Nadir ERSEN, Timuçin BARDAK, Uğur Can USTA
Bartın Orman Fakültesi Dergisi.2023; 25(3): 398. CrossRef - Pooled rates and demographics of POTS following SARS-CoV-2 infection versus COVID-19 vaccination: Systematic review and meta-analysis
Shin Jie Yong, Alice Halim, Shiliang Liu, Michael Halim, Ahmad A. Alshehri, Mohammed A. Alshahrani, Mohammed M. Alshahrani, Amal H. Alfaraj, Lamees M. Alburaiky, Faryal Khamis, Muzaheed, Bashayer M. AlShehail, Mubarak Alfaresi, Reyouf Al Azmi, Hawra Alba
Autonomic Neuroscience.2023; 250: 103132. CrossRef - Rapid suture-free repair of arterial bleeding: A novel approach with ultra-thin bioadhesive hydrogel membrane
Siwei Luo, Long Yang, Qiang Zou, Daizhu Yuan, Shunen Xu, Yanchi Zhao, Xin Wu, Zhen Wang, Chuan Ye
Chemical Engineering Journal.2023; 472: 144865. CrossRef - The Relationship Between Obsessive-Compulsive Disorder and Gaming Disorder
Nazir Hawi, Maya Samaha
International Journal of Cyber Behavior, Psychology and Learning.2023; 13(1): 1. CrossRef - Microbiological Quality and Presence of Foodborne Pathogens in Raw and Extruded Canine Diets and Canine Fecal Samples
Doina Solís, Magaly Toro, Paola Navarrete, Patricio Faúndez, Angélica Reyes-Jara
Frontiers in Veterinary Science.2022;[Epub] CrossRef - Stapler Assisted Total Laryngectomy: A Prospective Randomized Clinical Study
Omar Ahmed, Hesham Mustafa Abdel-Fattah, Hisham E. M. Elbadan
Indian Journal of Otolaryngology and Head & Neck Surgery.2022; 74(S2): 2205. CrossRef - Project VLOGI (Video Lectures on Giving Instructions): Effects on Learners’ Performance in Probability and Statistics
Sherwin BATİLANTES
International Journal of Educational Studies in Mathematics.2021; 8(4): 299. CrossRef
Statistical notes for clinical researchers: the independent samples
t -test
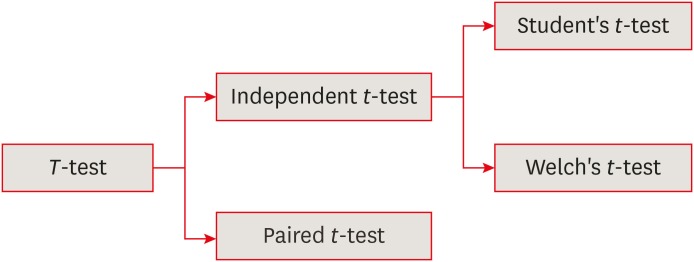
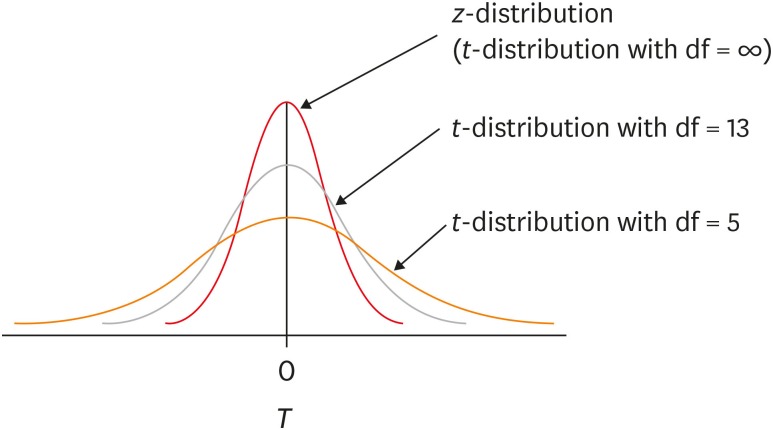
Figure 1 Types of 2-sample t-test.
Figure 2 The t-distribution with various degrees of freedom (df)
compared to z-distribution.
Figure 1
Figure 2
Statistical notes for clinical researchers: the independent samples
t -test
Descriptive statistics and result of the Student's t-test
| Group | No. | Mean | Standard deviation | p value |
|---|---|---|---|---|
| 1 | 10 | 10.28 | 0.5978 | 0.004 |
| 2 | 10 | 11.08 | 0.4590 |
Table 1 Descriptive statistics and result of the Student's
t-test

 KACD
KACD
 ePub Link
ePub Link Cite
Cite