Articles
- Page Path
- HOME > Restor Dent Endod > Volume 43(3); 2018 > Article
- Open Lecture on Statistics Statistical notes for clinical researchers: simple linear regression 2 – evaluation of regression line
-
Hae-Young Kim

-
Restor Dent Endod 2018;43(3):e34.
DOI: https://doi.org/10.5395/rde.2018.43.e34
Published online: August 9, 2018
Department of Health Policy and Management, College of Health Science, and Department of Public Health Science, Graduate School, Korea University, Seoul, Korea.
- Correspondence to Hae-Young Kim, DDS, PhD. Professor, Department of Health Policy and Management, Korea University College of Health Science, and Department of Public Health Science, Korea University Graduate School, 145 Anam-ro, Seongbuk-gu, Seoul 02841, Korea. kimhaey@korea.ac.kr
Copyright © 2018. The Korean Academy of Conservative Dentistry
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
- 1,912 Views
- 31 Download
- 5 Crossref
USEFULLNESS OF REGRESSION LINE
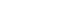
Depiction of comparative models: (A) a baseline model with mean of Y and its residuals (① Y − Ȳ, total variability); (B) fitted regression line using X and residuals (② Y − Ŷ, remaining residual); (C) the residual ① in (A) was divided into the explained variability by the line (③ Ŷ − Ȳ, explained variability due to regression) and reduced but remaining unexplained residual (②).
Calculation of sum of squares of total (SST), sum of squares due to regression (SSR), sum of squares of errors (SSE), and R-square, which is the proportion of explained variability (SSR) among total variability (SST)
A general form of analysis of variance table for the global evaluation of the regression line
| Source | Sum of squares | df | Mean squares | F |
|---|---|---|---|---|
| Regression | SSR = ∑(Ŷ − Y̅)2 | p | MSR = SSR/p | MSR/MSE |
| Residual | SSE = ∑(Y − Ŷ)2 | n − p − 1 | MSE = SSE/(n − p − 1) | |
| Total | SST = ∑(Y − Y̅)2 | n − 1 |
An analysis of variance (ANOVA) table for the example data
| ANOVA | |||||
|---|---|---|---|---|---|
| Model | Sum of squares | df | Mean square | F | p value |
| Regression | 1,475.036 | 1 | 1,475.036 | 20.947 | <0.001 |
| Residual | 1,267.514 | 18 | 70.417 | ||
| Total | 2,742.550 | 19 | |||
EVALUATION OF INDIVIDUAL SLOPE(S)
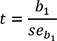 , where seb1 is the standard error of b1.
, where seb1 is the standard error of b1.Regression coefficients from the example data
Tables & Figures
REFERENCES
Citations

- Exploring soil pollution patterns in Ghana's northeastern mining zone using machine learning models
Daniel Kwayisi, Raymond Webrah Kazapoe, Seidu Alidu, Samuel Dzidefo Sagoe, Aliyu Ohiani Umaru, Ebenezer Ebo Yahans Amuah, Prosper Kpiebaya
Journal of Hazardous Materials Advances.2024; 16: 100480. CrossRef - Influence of the radius of Monson’s sphere and excursive occlusal contacts on masticatory function of dentate subjects
Dominique Ellen Carneiro, Luiz Ricardo Marafigo Zander, Carolina Ruppel, Giancarlo De La Torre Canales, Rubén Auccaise-Estrada, Alfonso Sánchez-Ayala
Archives of Oral Biology.2024; 159: 105879. CrossRef - Application of hot air-derived RSM conditions and shading for solar drying of avocado pulp and its properties
Sitanan Kowarit, Kitti Sathapornprasath, Surachai Narrat Jansri
Solar Energy.2024; 278: 112768. CrossRef - Corrosion Behavior of Alloy 22 According to Hydrogen Sulfide, Chloride, and pH in an Anaerobic Environment
Yun-Ho Lee, Jin-Seok Yoo, Yong-Won Kim, Jung-Gu Kim
Metals and Materials International.2024; 30(7): 1878. CrossRef - Classification of Male Athletes Based on Critical
Power
Javier Olaya-Cuartero, Basilio Pueo, Alfonso Penichet-Tomas, Jose M. Jimenez-Olmedo
International Journal of Sports Medicine.2024; 45(09): 678. CrossRef
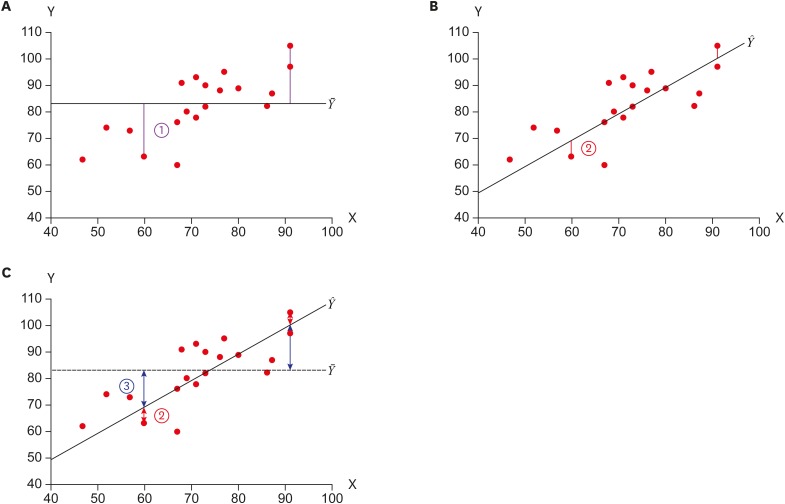
Figure 1
Calculation of sum of squares of total (SST), sum of squares due to regression (SSR), sum of squares of errors (SSE), and R-square, which is the proportion of explained variability (SSR) among total variability (SST)
| No | X | Y | ① Y − Y̅ | (Y − Y̅)2 | Ŷ | ③ Ŷ − Y̅ | (Ŷ − Y̅)2 | ② Y − Ŷ | (Y − Ŷ)2 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 73 | 90 | 7.65 | 58.52 | 82.74 | 0.39 | 0.15 | 7.26 | 52.68 |
| 2 | 52 | 74 | −8.35 | 69.72 | 67.80 | −14.55 | 211.75 | 6.20 | 38.46 |
| 3 | 68 | 91 | 8.65 | 74.82 | 79.18 | −3.17 | 10.02 | 11.82 | 139.62 |
| 4 | 47 | 62 | −20.35 | 414.12 | 64.24 | −18.11 | 327.96 | −2.24 | 5.02 |
| 5 | 60 | 63 | −19.35 | 374.42 | 73.49 | −8.86 | 78.48 | −10.49 | 110.06 |
| 6 | 71 | 78 | −4.35 | 18.92 | 81.32 | −1.03 | 1.06 | −3.32 | 11.01 |
| 7 | 67 | 60 | −22.35 | 499.52 | 78.47 | −3.88 | 15.04 | −18.47 | 341.22 |
| 8 | 80 | 89 | 6.65 | 44.22 | 87.72 | 5.37 | 28.87 | 1.28 | 1.63 |
| 9 | 86 | 82 | −0.35 | 0.12 | 91.99 | 9.64 | 92.98 | −9.99 | 99.85 |
| 10 | 91 | 105 | 22.65 | 513.02 | 95.55 | 13.20 | 174.26 | 9.45 | 89.29 |
| 11 | 67 | 76 | −6.35 | 40.32 | 78.47 | −3.88 | 15.04 | −2.47 | 6.11 |
| 12 | 73 | 82 | −0.35 | 0.12 | 82.74 | 0.39 | 0.15 | −0.74 | 0.55 |
| 13 | 71 | 93 | 10.65 | 113.42 | 81.32 | −1.03 | 1.06 | 11.68 | 136.46 |
| 14 | 57 | 73 | −9.35 | 87.42 | 71.36 | −10.99 | 120.86 | 1.64 | 2.70 |
| 15 | 86 | 82 | −0.35 | 0.12 | 91.99 | 9.64 | 92.98 | −9.99 | 99.85 |
| 16 | 76 | 88 | 5.65 | 31.92 | 84.88 | 2.53 | 6.38 | 3.12 | 9.76 |
| 17 | 91 | 97 | 14.65 | 214.62 | 95.55 | 13.20 | 174.26 | 1.45 | 2.10 |
| 18 | 69 | 80 | −2.35 | 5.52 | 79.90 | −2.45 | 6.03 | 0.10 | 0.01 |
| 19 | 87 | 87 | 4.65 | 21.62 | 92.70 | 10.35 | 107.21 | −5.70 | 32.54 |
| 20 | 77 | 95 | 12.65 | 160.02 | 85.59 | 3.24 | 10.49 | 9.41 | 88.58 |
| Y̅ = 82.35 | SST = ∑[Y − Y̅]2 = 2,742.55 | SSR = ∑[Ŷ − Y̅]2 = 1,475.04 | SSE = ∑[Y − Ŷ]2 = 1,267.51 | ||||||
| R2 = SSR/SST = 1,475.04/2,742.55 = 0.538 | |||||||||
Ŷ = 30.79 + 0.71X.
A general form of analysis of variance table for the global evaluation of the regression line
| Source | Sum of squares | df | Mean squares | F |
|---|---|---|---|---|
| Regression | SSR = ∑(Ŷ − Y̅)2 | p | MSR = SSR/p | MSR/MSE |
| Residual | SSE = ∑(Y − Ŷ)2 | n − p − 1 | MSE = SSE/(n − p − 1) | |
| Total | SST = ∑(Y − Y̅)2 | n − 1 |
df, degrees of freedom; SSR, sum of squares due to regression; MSR, mean of squares of regression; MSE, mean of squares of error; SSE, sum of squares of error; n, number of observation; p, number of predictor variables (Xs) in the model; SST, sum of squares of total.
An analysis of variance (ANOVA) table for the example data
| ANOVA | |||||
|---|---|---|---|---|---|
| Model | Sum of squares | df | Mean square | F | p value |
| Regression | 1,475.036 | 1 | 1,475.036 | 20.947 | <0.001 |
| Residual | 1,267.514 | 18 | 70.417 | ||
| Total | 2,742.550 | 19 | |||
Table was cited from appendix of reference [
df, degree of freedom.
Regression coefficients from the example data
| Coefficients | |||||||
|---|---|---|---|---|---|---|---|
| Model | Unstandardized coefficients | Standardized coefficients | t | p value | 95% CI for bound | ||
| B | SE | Beta | Lower bound | Upper bound | |||
| 1 (Constant) | 30.795 | 11.420 | 2.697 | 0.015 | 6.803 | 54.787 | |
| X | 0.712 | 0.155 | 0.733 | 4.577 | 0.000 | 0.385 | 1.038 |
Table was cited from appendix of reference [
SE, standard error; CI, confidence interval.
df, degrees of freedom; SSR, sum of squares due to regression; MSR, mean of squares of regression; MSE, mean of squares of error; SSE, sum of squares of error; n, number of observation; p, number of predictor variables (Xs) in the model; SST, sum of squares of total.
Table was cited from appendix of reference [
df, degree of freedom.
Table was cited from appendix of reference [
SE, standard error; CI, confidence interval.

 KACD
KACD
 ePub Link
ePub Link Cite
Cite