Articles
- Page Path
- HOME > Restor Dent Endod > Volume 41(4); 2016 > Article
- Open Lecture on Statistics Statistical notes for clinical researchers: Definition and comparison of risk and odds
- Hae-Young Kim
-
2016;41(4):-340.
DOI: https://doi.org/10.5395/rde.2016.41.4.338
Published online: October 4, 2016
Department of Health Policy and Management, College of Health Science, and Department of Public Health Sciences, Graduate School, Korea University, Seoul, Korea.
- Correspondence to Hae-Young Kim, DDS, PhD. Associate Professor, Department of Health Policy and Management, College of Health Science, and Department of Public Health Sciences, Graduate School, Korea University, 145 Anam-ro, Seongbukgu, Seoul, Korea 02841. TEL, +82-2-3290-5667; FAX, +82-2-940-2879; kimhaey@korea.ac.kr
©Copyrights 2016. The Korean Academy of Conservative Dentistry.
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
- 811 Views
- 11 Download
One of the most frequently used outcomes in health studies is the status of disease, such as having disease or not having disease. A probability of having a disease is referred as a risk of a disease, as a basic term used in description of such a binary disease state. Also risk difference or risk ratio is used in comparison of risks among two or more groups. Different from risk, an odds by itself is not as frequently mentioned as risk. However odds ratio meaning ratio of two odds is very popular because it is the same value with an exponentiated regression coefficient from a logistic regression, i.e., exp(beta). To understand concept and usage of risk- and odds-related terms better, we will first talk about risk and odds briefly in this section.
Ratio and proportion
A ratio is defined as an expression of a measure relative to another. When you compare two quantities, how many times one is to another is called a ratio. If we have a group with 20 males and 80 females, the ratio of men to women is expressed as 20/80 = 0.25. A proportion is a type of ratio that relates a part to a whole. In the example, we can calculate the proportion of men is 20/100 = 0.2, or 20% as the total size is 100. Similarly the proportion of women is 80/100 = 0.8, or 80%.
Risk and odds of a disease
Risk is defined as the potential of losing something of value, such as physical health, social status, or financial wealth. Risk is the possibility of disease, injury, loss, or other adverse or unwelcomed circumstances. If we have no other information but disease state, we can assume that different disease state occurs only by chance. Each subject in the whole group has the same chance or possibility to get the disease state. In other words, the risk of the disease is the same for everyone and the disease state occurs at random. In that circumstance, the proportion of having the disease represents the risk that a person has the disease. In Table 1, if we don't consider the information of exposure states, the risk of disease is simply number of events divided by the total cases, (a + c) / (a + b + c + d). Risk is the proportion of disease, generally represented by 'p'.
The odds is expressed as the ratio of events to non-events. If we disregard exposure state, the odds of disease is expressed as (a + c) / (b + d).
Table 2 shows various combination of events and non-events and their risk (= proportion) and odds. While the risk ranges from 0 to 1, odds value ranges from 0 to infinity. When the numbers of event and non-event are equal, the proportion is 500/1,000 = 0.5 and the odds is 500/500 = 1. The values of odds and risk are similar only when the event occurs very rarely and the risk is small, e.g., less than 0.05, in Table 2. Therefore we can use the odds as a proxy of risk only when occurrence of the event is very rare.
Mathematical relationship of risk and odds
Also there is a mathematical relationship between risk and odds as follows:
Figure 1 shows a schematic expression of the relationship between risk and odds. We can notice that as the risk, p, changes from 0 to 1, corresponding odds value ranges from 0 to infinity.
Calculating risk and odds in various conditions using an example
Table 3 provides an example of lung cancer and smoking status. We can calculate risk and odds of having lung cancer in total population as p = 15/165 = 0.091 (= 9.1%) and odds = 15/150 = 0.1. Here risk and odds show a little difference. Also risk and odds of smoking in total population are p = 60/165 = 0.364 (= 36.4%) and odds = 60/105 = 0.57, respectively. As for risk and odds of having lung cancer in smoking population are p = 10/60 = 0.167 (16.7%) and odds = 10/50 = 0.2. Similarly risk and odds of having lung cancer in non-smoking population are p = 5/105 = 0.048 (4.8%) and odds = 5/100 = 0.05. Inversely risk and odds of smoking in population having lung cancer are p = 10/15 = 0.667 (66.7%) and odds = 10/5 = 2. Similarly risk and odds of smoking in population not having lung cancer are p = 50/150 = 0.333 (33.3%) and odds = 50/100 = 0.5.
Based on these simple calculations of risk and odds in various conditions, we could expand our understanding on risk ratio and odds ratio in the next statistical note.
Table 1
An example of 2*2 cross table
| Disease | No disease | Total | |
|---|---|---|---|
| Exposure | a | b | a + b |
| No exposure | c | d | c + d |
| Total | a + c | b + d | a + b + c + d |
Table 2
Comparison of risk (p = proportion) and odds (total n = 1,000)
Table 3
An example of lung cancer and smoking state, N (%)
Tables & Figures
REFERENCES
Citations
Citations to this article as recorded by 

Statistical notes for clinical researchers: Definition and comparison of risk and odds
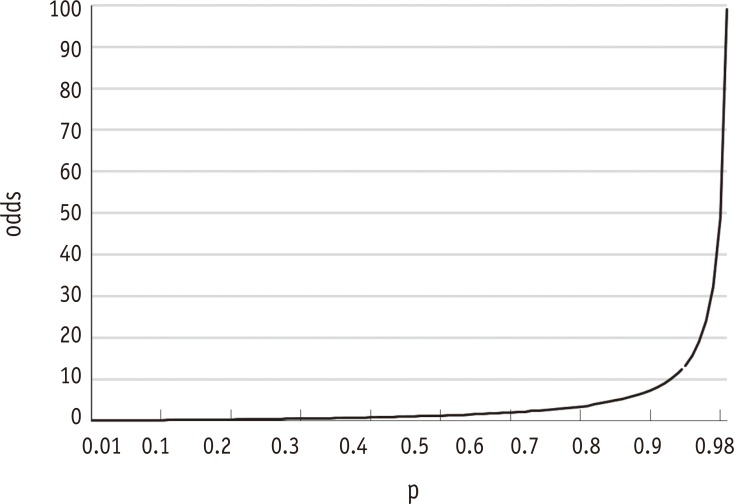
Figure 1 Relationship between risk (p = proportion) and odds.
Figure 1
Statistical notes for clinical researchers: Definition and comparison of risk and odds
An example of 2*2 cross table
| Disease | No disease | Total | |
|---|---|---|---|
| Exposure | a | b | a + b |
| No exposure | c | d | c + d |
| Total | a + c | b + d | a + b + c + d |
Comparison of risk (p = proportion) and odds (total n = 1,000)
| No. of event | 1 | 10 | 20 | 50 | 100 | 500 | 900 | 999 |
|---|---|---|---|---|---|---|---|---|
| No. of non-event | 999 | 990 | 980 | 950 | 900 | 500 | 100 | 1 |
| Risk (= p) | 1 / 1,000 = 0.001 | 10 / 1,000 = 0.01 | 20 / 1,000 = 0.02 | 50 / 1,000 = 0.05 | 100 / 1,000 = 0.1 | 500 / 1,000 = 0.5 | 900 / 1,000 = 0.9 | 999 / 1,000 = 0.999 |
| Odds | 1 / 999 = 0.001 | 10 / 990 = 0.0101 | 20 / 980 = 0.0204 | 50 / 950 = 0.0526 | 100 / 900 = 0.1111 | 500 / 500 = 1 | 900 / 100 = 9 | 999 / 1 = 999 |
An example of lung cancer and smoking state, N (%)
| Lung cancer | No lung cancer | Total | ||
|---|---|---|---|---|
| Smoking | Count | 10 | 50 | 60 |
| % within smoking | 16.7% | 83.3% | 100.0% | |
| % within lung cancer | 66.7% | 33.3% | 36.4% | |
| % of total | 6.1% | 30.3% | 36.4% | |
| No smoking | Count | 5 | 100 | 105 |
| % within smoking | 4.8% | 95.2% | 100.0% | |
| % within lung cancer | 33.3% | 66.7% | 63.6% | |
| % of total | 3.0% | 60.6% | 63.6% | |
| Total | Count | 15 | 150 | 165 |
| % within smoking | 9.1% | 90.9% | 100.0% | |
| % within lung cancer | 100.0% | 100.0% | 100.0% | |
| % of total | 9.1% | 90.9% | 100.0% |
Table 1 An example of 2*2 cross table
Table 2 Comparison of risk (p = proportion) and odds (total n = 1,000)
Table 3 An example of lung cancer and smoking state, N (%)

 KACD
KACD
 ePub Link
ePub Link Cite
Cite