KACD
Articles
- Page Path
- HOME > Restor Dent Endod > Volume 33(3); 2008 > Article
- Original Article The influence of occlusal loads on stress distribution of cervical composite resin restorations: A three-dimensional finite element study
- Chan-Seok Park1, Bock Hur1, Hyeon-Cheol Kim1, Kwang-Hoon Kim2, Kwon Son2, Jeong-Kil Park1
-
2008;33(3):-257.
DOI: https://doi.org/10.5395/JKACD.2008.33.3.246
Published online: May 31, 2008
1Department of Conservative Dentistry, School of Dentistry, Pusan National University, Korea. JFIF d d Ducky d qhttp://ns.adobe.com/xap/1.0/ |er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE &ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ >=F)2[nk؆?훐 M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag% qkEUzUgæBhߕP(7]kFnq?֖Cpru Z6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p \̅S?㭻;t~ R߁ )^/>Qj`yt[w ԛ;² ~+ ߔ_ YW~|o] ?x^ᯛ `ʼn;g)T@vWn]>&4l p+$D̢1l|ȨF%-} .9[}w~
ԠLM9hСablfe&QoW !s ?wjLK?s7yO>(=C~_nyǜu? v 3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw= /7ovuk+\V;lDgն <[A+r X~d;m!_s8ݖ;;.0llUC+?i#_crʙ1~C.\q u l8Hܶ2m`ܻM3Tov|Bs rɵ"oLS-
DКw=Tv@f '6|YlD͓Y%-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~
&f#
}o!muH; ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{
m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ
dng>ەZ,Mmϑ :n6nϦezW qUJ4! ۇ4R! =>>F n|Q[{pRO 17ƕ~._I ''00k=b՛o}Osðc2'o\3}ݭQ^ 2 . R1yKȣtAݿ-u ܾw!`?1Whn|gzU o[ECWwjUIן)^h#1ɭ!/Z
np;o;ΗŻkXs."6E`Z1
עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV 2`y/0E˛6+ԫ1?
6}KW c\KoKͨ2ۅFws*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* P RaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ
^˒4kƓmzDx
\
'Nq amP7nyN݅=
2Department of Mechanical Design Engineering, College of Engineering, Pusan National University, Korea. JFIF d d Ducky d qhttp://ns.adobe.com/xap/1.0/ |er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE &ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ >=F)2[nk؆?훐 M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag% qkEUzUgæBhߕP(7]kFnq?֖Cpru Z6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p \̅S?㭻;t~ R߁ )^/>Qj`yt[w ԛ;² ~+ ߔ_ YW~|o] ?x^ᯛ `ʼn;g)T@vWn]>&4l p+$D̢1l|ȨF%-} .9[}w~
ԠLM9hСablfe&QoW !s ?wjLK?s7yO>(=C~_nyǜu? v 3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw= /7ovuk+\V;lDgն <[A+r X~d;m!_s8ݖ;;.0llUC+?i#_crʙ1~C.\q u l8Hܶ2m`ܻM3Tov|Bs rɵ"oLS-
DКw=Tv@f '6|YlD͓Y%-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~
&f#
}o!muH; ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{
m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ
dng>ەZ,Mmϑ :n6nϦezW qUJ4! ۇ4R! =>>F n|Q[{pRO 17ƕ~._I ''00k=b՛o}Osðc2'o\3}ݭQ^ 2 . R1yKȣtAݿ-u ܾw!`?1Whn|gzU o[ECWwjUIן)^h#1ɭ!/Z
np;o;ΗŻkXs."6E`Z1
עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV 2`y/0E˛6+ԫ1?
6}KW c\KoKͨ2ۅFws*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* P RaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ
^˒4kƓmzDx
\
'Nq amP7nyN݅=
- Corresponding Author: Jeong-Kil Park. Department of Conservative Dentistry, School of Dentistry, Pusan National University, 1-10, Ami-dong, Seo-gu, Busan 602-739, Korea. Tel: 82-51-240-7456, jeongkil@pusan.ac.kr
• Received: April 14, 2008 • Revised: April 24, 2008 • Accepted: April 30, 2008
Copyright © 2008 The Korean Academy of Conservative Dentistry
- 1,510 Views
- 10 Download
- 2 Crossref
Abstract
- The purpose of this study was to investigate the influence of various occlusal loading sites and directions on the stress distribution of the cervical composite resin restorations of maxillary second premolar, using 3 dimensional (3D) finite element (FE) analysis. Extracted maxillary second premolar was scanned serially with Micro-CT (SkyScan1072; SkyScan, Aartselaar, Belgium). The 3D images were processed by 3D-DOCTOR (Able Software Co., Lexington, MA, USA). HyperMesh (Altair Engineering, Inc., Troy, USA) and ANSYS (Swanson Analysis Systems, Inc., Houston, USA) was used to mesh and analyze 3D FE model. Notch shaped cavity was filled with hybrid (Z100, 3M Dental Products, St. Paul, MN, USA) or flowable resin (Tetric Flow, Vivadent Ets., FL-9494-Schaan, Liechtenstein) and each restoration was simulated with adhesive layer thickness (40 µm). A static load of 200 N was applied on the three points of the buccal incline of the palatal cusp and oriented in 20° increments, from vertical (long axis of the tooth) to oblique 40° direction towards the buccal. The maximum principal stresses in the occlusal and cervical cavosurface margin and vertical section of buccal surfaces of notch-shaped class V cavity were analyzed using ANSYS. As the angle of loading direction increased, tensile stress increased. Loading site had little effect on it. Under same loading condition, Tetric Flow showed relatively lower stress than Z100 overall, except both point angles. Loading direction and the elastic modulus of restorative material seem to be important factor on the cervical restoration.
I. INTRODUCTION
Non-carious cervical lesion (NCCL) is the loss of hard dental tissue commonly observed at the buccal and labial tooth surfaces at the cementoenamel junction (CEJ).
Most NCCLs of teeth can be classified into four categories: attrition, erosion, abrasion, and stress-induced cervical lesion. Stress-induced cervical lesions are loss of tooth structure that results from repeated tooth flexure caused by occlusal stresses. These lesions are generally wedge shaped and were previously termed idiopathic cervical erosion lesion, later called abfractions by Grippo1).
For abfraction, it has been postulated that the cervical fulcrum area of a tooth is subject to unique stress, torque and moments resulting from occlusal function, bruxing and parafunctional activity2).
Clinically, these lesions have sharp, angular, wedge-shaped defects principally found on the buccal and labial aspects of the teeth. According to Telles et al.3), the most commonly affected teeth are the maxillary premolars.
Grippo4) suggested that abfraction is the basic cause of all NCCLs, whereas Lee and Eakle5) proposed a multifactorial etiology, with a combination of occlusal stress, abrasion, and erosion.
There is some clinical evidence for the association of abfraction lesions with heavy occlusal loads. For example, Xhonga6) found the prevalence of these lesions to be significantly higher in patients who were bruxists, while Lambrechts et al.7) found that bruxism and malocclusion were associated with abfraction lesions.
Some authors2,8,9) have proposed the interesting idea that large tensile stresses by occlusal loading may cause a loss of tooth structure. When mastication is not ideal, lateral forces appear which cause the tooth to bend. Lee and Eakle5) later hypothesized that the primary etiologic factor in wedge-shaped cervical erosion is tensile stress from mastication and malocclusion.
It is suggested that occlusal loads applied during lateral excursion cause the tooth flex. As the tooth flexes, these stresses may cause disruption of the bonds between the hydroxyapatite crystals leading to enamel loss. The abfraction is accelerated by excessive occlusal load such as occlusal interferences, premature contacts, bruxism, and clenching habit10).
Loss of tooth structure in the cervical area of a NCCLs may cause esthetic problems and discomfort due to dentinal hypersensitivity1,3,6), but not all lesions require restorations11). The decision to restore NCCLs is based on the desire to strengthen the tooth and decrease the theoretical stress concentration and flexure, mitigate lesion progression, prevent hypersensitivity and pulp involvement, improve oral hygiene and enhance esthetics11,12).
Tooth-colored direct restorative materials such as glass ionomer cement, composite resins, and resin-modified glass ionomer are available13). The most appropriate one is composite resin, in spite of some disadvantages like time-consuming, technique-sensitive, volumetric shrinkage, which can also exhibit superior esthetics, polishability, wear resistance. Some authors14-16) suggested that the use of more flexible restorative materials may be able to resist shear forces generated by tooth flexure and therefore enhance retention.
Decrease of tooth overloads by adjusting occlusion, elimination of parafunction, or fabrication of occlusal splints may limit formation of these lesions.
Lambrechts et al.7) pointed out that if the occlusion is not corrected, premature loss of the cervical restoration results because the restoration is subjected to the same tensile force that can cause debonding, leakage, and retention failure.
Importantly, the para-axial loading is a major determinant of increased tensile stresses resulting in mechanical failure of cervical restorations.
When the load was applied vertically to the tooth, either to the tip of the buccal cusp or the lingual cusp, the lowest maximum principal stress values were found. The oblique loads applied to the inner aspects of the buccal or lingual cusp slopes produced the highest maximum principal stress values. The reason for these very high stress values is that the cusps of these teeth were acting like a cantilever beam17).
From studies of occlusal loading direction, Ichim et al.18) applied a force of 200 N on the tip of buccal cusp of lower first premolar and oriented in 10° increments, from vertical to oblique 40° direction towards the buccal. Lee et al.19) applied loading on buccal and lingual cusp tip of maxillary second premolar at vertical, buccally 45° and lingually 45° direction to the long axis, each with 170 N.
Although there were several studies18-21) on occlusal loading direction, there were few studies on the role of both direction and location.
The purpose of this study was to investigate the influence of various occlusal loading sites and directions on the stress distribution of the cervical composite resin restorations of maxillary second premolar, using 3 dimensional (3D) finite element (FE) analysis.
II. MATERIALS AND METHODS
To develop a 3D FE model, intact normal extracted human maxillary second premolars were used. The extracted premolars were scanned serially with micro-CT (SkyScan1072; SkyScan, Aartselaar, Belgium) to expose the tooth sections perpendicular to the long axis of the tooth (58 µm in thickness) and parallel to the occlusal plane. Image processing software, 3D-DOCTOR (Able Software Co., Lexington, MA, USA), was employed to make the boundaries of enamel, dentin and pulp and to construct a surface model of tooth from the sectioned two dimensional images. HyperMesh Ver. 6 (Altair Engineering, Inc., Troy, USA) and ANSYS Ver. 9 (Swanson Analysis Systems, Inc., Houston, USA) were used to mesh and analyze 3D FE model.
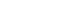
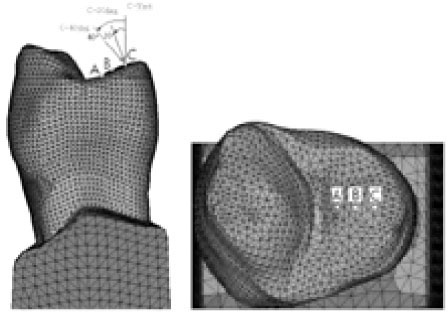
The final model consisted of 13025 elements with 19628 nodes, the 3D meshed maxillary premolar with notch-shaped class V restoration is shown in Figure 1.
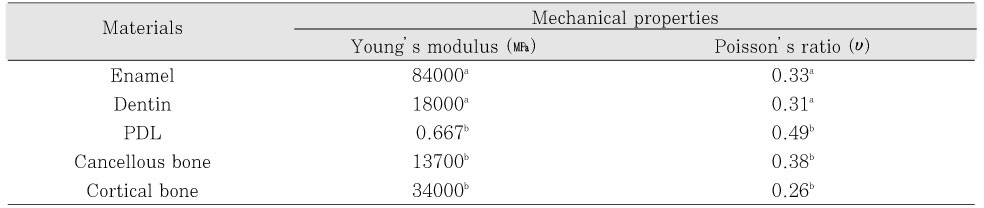
The physical properties of the tooth and supporting structures used in this study are given in Table 1. All the vital tissues were presumed linearly elastic, homogeneous and isotropic. The corresponding elastic properties such as Young's modulus and Poisson's ratio were determined according to literature survey22,23).
The periodontal ligament was assumed to be 0.3 mm wide, and the dimensions of surrounding compact and cancellous bone were derived from standard texts24,25). The alveolar bone was also generated by growing the outer surface of the tooth model from 2 mm below the CEJ.
The model was fixed on mesiodistal direction. In all loading cases, the base nodes of simulated alveolar bone were assumed fixed to prevent rigid body motion.
1. Restorative materials
Notch-shaped class V cavity was filled with either conventional hybrid or flowable resin.
The data of material properties such as elastic modulus, Poisson's ratio used in this study were obtained by literature review22,26) (Table 2). The Z100 (3M Dental Products, St. Paul, MN, USA) was used as representatives of hybrid composite resin and Tetric Flow (Vivadent Ets., FL-9494-Schaan, Liechtenstein) as flowable resin. The dentin bonding system used in this study was Scotchbond MP (3M Dental Products, St. Paul, MN, USA). The adhesive layer of 40 µm was made by mathematical shell element modeling and the conjunctions between materials were set as complete coupling.
2. Loading conditions
As in Figure 2, a point load of 200 N was applied on the three points of the buccal incline of the palatal cusp and oriented in 20° increments, from vertical (long axis of the tooth) to oblique 40° direction towards the buccal.
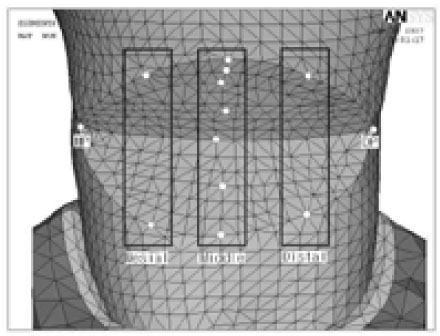
The maximum principal stresses in the occlusal and cervical cavosurface margin and vertical section of buccal surfaces of notch-shaped class V cavity were analyzed using ANSYS. The nodal distribution for stress analysis was presented at Figure 3.
III. RESULTS
(1) Pattern of stress distribution
Maximum principal stress increased as the angle of loading direction increased at each loading site. Under same loading direction, stress increased as loading site moved from A to C. Both Z100 and Tetric Flow showed highest stress distribution at C-40 deg. Cervical cavosurface margin showed higher stress than occlusal cavosurface margin. In the cavity wall, cervical surface showed more stress than occlusal surface. Both Z100 and Tetric Flow showed highest stress concentration on cervical root dentin.
Under same loading condition, Tetric Flow showed relatively lower stress than Z100 (Figure 4 and 5).
(2) Analysis of stress
Analysis of stress along the occlusal cavosurface margin
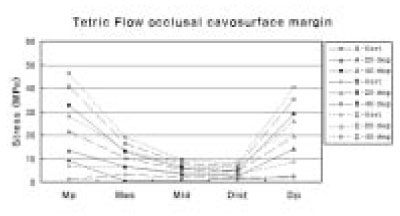
Z100 showed highest stress at C-40 deg and showed stress of 41.72 MPa at mesial point angle and 34.09 MPa at distal point angle. Stress decreased as it moved from mesial point angle to distal cavosurface margin and increased at distal point angle. Without regard to loading site, stress increased as the angle of loading direction increased. Except A-Vert of the mesial point angle, stress increased as loading site moved from A to C under same loading direction (Figure 6).
Tetric Flow also showed highest stress at C-40 deg and showed stress of 46.33 MPa at mesial point angle and 40.46 MPa at distal point angle. Tetric Flow showed similar pattern to Z100 but, except mesial point angle and distal point angle, it showed relatively lower stress than Z100 overall (Figure 7).
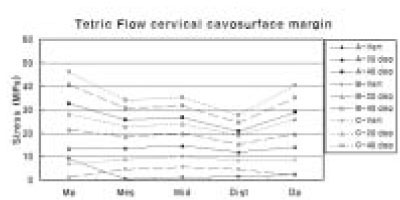
Analysis of stress along the cervical cavosurface margin
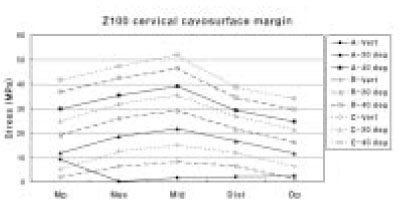
In case of restoration using Z100, it showed highest stress at C-40 deg and had 51.92 MPa peak tensile stress value at the middle area. Stress increased as it moved from mesial point angle to middle cavosurface margin and decreased at distal point angle. Without regard to loading site, stress increased as the angle of loading direction increased. Under same loading direction, except A-Vert of the mesial point angle, stress increased as loading site moved from A to C (Figure 8).
Tetric Flow showed highest stress at C-40 deg. However, unlike Z100, stress decreased as it moved from mesial point angle to distal cavosurface margin and increased at distal point angle. Under same loading direction, except A-Vert of the mesial point angle, stress increased as loading site moved from A to C (Figure 9).
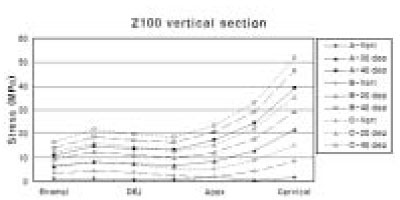
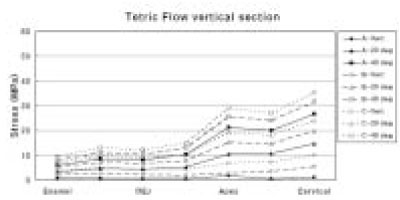
Analysis of stress along the vertical section of cavity
Z100 showed value of 51.92 MPa of peak tensile stress at the cervical cavosurface margin. Stress increased as it moved from enamel cavosurface margin to cervical cavosurface margin. Under same loading direction, stress increased as loading site moved from A to C (Figure 10).
Tetric Flow showed value of 35.33 MPa of peak tensile stress at the cervical cavosurface margin. Stress increased as it moved from enamel cavosurface margin to cervical cavosurface margin. However, unlike Z100, stress increased at the apex. Under same loading direction, stress increased as loading site moved from A to C. But, showed relatively lower stress than Z100 overall (Figure 11).
IV. DISCUSSION
Different types of functional and parafunctional activities that occur in the mouth, such as chewing and bruxing, significantly influence the rupture of the tooth structure. When a tooth is loaded in the long axis, the forces are dissipated with minimal stress in the dentin or enamel. If the direction of the force is moved laterally, however, teeth are flexed toward both sides. The stress pattern in the same area is changed continuously from compressive to tensile, especially underneath the enamel, since dentin appears to be substantially stronger than enamel when under lateral forces. Thus, the cyclic occurrence of compression and tension may reach the fatigue limit and lead to rupture of the chemical bonds between the hydroxyapatite crystals5,27,28).
Posterior teeth were more likely to exhibit NCCLs, possibly owing to the fact that greater occlusal forces and more lateral forces are exerted in the posterior teeth. Maxillary teeth seem more prone to NCCLs, possibly owing to the lingual tilt. Premolars, in particular first premolars, appeared to have the highest prevalence of NCCLs29).
In order to determine the load conditions such as magnitudes, directions, occlusal contacts (i.e., point or surface, centric or eccentric), preliminary investigation was performed using the data gathered by literature review30,31). Based upon these data, 170 N was assumed as the chewing force for premolars and 500 N was assumed as the heavy parafunctional load of bruxism and traumatic occlusion. The chewing forces produced by mastication are reported to range from approximately 37 - 40% of the maximum bite force32).
Lee et al.19) developed 3D FE analysis of maxillary premolar, which was loaded with static 170 N using seven load conditions of various load sites and different directions. Borcic et al.20) and Ichim et al.18) also went on an experiment with 200 N of loading. Therefore, stress range of intraoral loading seems to be within the value of 170 - 200 N. In this study, a tooth model loaded by a point load of static 200 N was considered more representative of normal chewing load situation, in contrast to other FE analysis studies23,33-35).
Previous studies18-20) were based on applying load on buccal cusp. However, applying load to palatal cusp arise tensile stress on cervical restoration of the buccal surface. Therefore load was only applied on palatal cusp in this study.
There were several studies18-21) on occlusal loading direction however, there were few studies on the role of both direction and location. Therefore, the objective of this study was to investigate the effects of direction and location of load on the cervical restoration.
Strains were concentrated near the CEJ regardless of load direction. A vertical load on the buccal cusp tip resulted in compressive strains on the buccal surface but small tensile strains in lingual cervical enamel. Strains resulting from oblique loads on buccal cusp inclines were complex and asymmetric, with either tension or compression occurring in any location depending on the site and angle of loading. The magnitude, direction and character of strains in cervical enamel are highly dependent on patterns of loading21).
According to results of this study, under same loading site, tensile stress increased as the angle of loading direction increased. Under same loading direction, tensile stress increased as loading site moved from A to C. Both Z100 and Tetric Flow showed highest stress distribution at C-40 deg. As the angle of loading direction increased, tensile stress increased. Loading site had little effect on it. Therefore, loading direction seems to be an important factor on the cervical restoration.
According to Ichim et al.18), it is shown that the direction of loading is a major determinant for the maximum tensile stress and also the stress gradient along the restoration's interfaces. Axial and oblique loading up to 20° induced moderate tensile stresses, whereas loads inclined at 30° and 40° dramatically increased tensile loading on the fillings. This study also had same results.
After restoration of NCCLs, restored teeth are also subjected to the physical forces of mastication with their attendant compressive, tensile, shear and bending forces. Heymann et al.36) have proposed a tooth-flexure theory to explain the failure of class V restorations and have suggested that two mechanisms operate to produce failure. First, lateral excursive movements result in lateral cuspal movement that generates tensile stress along the tooth - restoration interface. In addition, heavy forces in centric occlusion cause vertical deformation of the tooth leading to damaging compressive and shear stresses at the tooth - restoration interface. Concentration of compressive and tensile stresses at the cervical area induced by eccentric or heavy centric occlusal forces may progressively dislodge and eventually debond resin restorations. After treating cervical lesions with a variety of class V restorations, researchers37) found that the rate of progress of the destruction decreased from an average of 7 µm to 2 µm a week.
In our experiment, lesions were restored by two materials having different elastic modulus materials, conventional hybrid resin and flowable resin. From this experiment, under same loading condition, Tetric Flow showed relatively lower stress than Z100 overall except both point angles.
Clinical trial data from Heymannn et al.36,38) indicated a significantly greater retention failure rate in cervical lesions restored with a macrofilled composite resin compared to those restored with a microfilled resin. This is consistent with the lower modulus of elasticity of microfilled resins allowing the restoration to flex with the tooth rather than debond. Van Meerbeek et al.39) confirmed the correlation of improved clinical results with lower moduli of elasticity.
In this study, both Z100 and Tetric Flow showed highest stress concentration on cervical root dentin. And cervical cavosurface margin showed higher stress than occlusal cavosurface margin.
In addition, mesial point angle showed higher stress than distal point angle. Because of the anatomical mesiodistal asymmetry, higher stresses were concentrated at mesial point angle than distal point angle.
Z100 showed lower stress than Tetric Flow at each point angle as well as at the apex of vertical section of the cavity. It was hypothesized that Z100 composites used as a strut would improve the reduction rates of stress in the apex. This hypothesis was based on earlier studies40) showing that restoration using Z100 worked as a strut to prevent stress concentration of the lesion.
Tetric Flow showed relatively lower stress than Z100 in the cervical cavosurface margin and occlusal cavosurface margin. Because low modulus materials can flex with the tooth and therefore can remain in situ. Thus, these resins will absorb much of the masticatory stresses rather than transferring it to the dentin-restoration interface41). A low elastic modulus also contributes to stress relief from polymerization shrinkage of composites, preserving the marginal integrity of restorations42). This property allows for good wetting along the cavity walls, which improves the adaptation of the restorative material.
If oblique force loading on teeth is the major cause of the cervical lesion, as suggested by our results, further attention should be paid to the importance of the occlusal adjustment for the treatment of cervical tooth defects.
Improvement of the retention of the restoration should be achieved by restorative material and occlusal adjustment. Occlusal adjustment should be done before the restoration of NCCLs to change the loading direction rather than loading site and it would be better to restore material which is capable of absorbing stress and of low modulus elasticity.
The result of this study must be interpreted with a certain amount of caution. In this study, the static load stresses may not reflect the actual conditions encountered intraorally, therefore may not adequately describe the functional movement of occlusion. The conjunctions between materials were assumed to be complete bonded but actually they were not. It was hard to include other factors that occur intraorally in this computer simulation.
In future, more studies on the different ways of changing loading direction by occlusal adjustment and more suitable restorative material for NCCLs seems to be necessary.
V. CONCLUSIONS
Within the limitations of our study, the following conclusion can be drawn:
As the angle of loading direction increased, tensile stress increased. Loading site had little effect on it. Under same loading condition, Tetric Flow showed relatively lower stress than Z100 overall, except both point angles. Therefore, loading direction and the elastic modulus of restorative material seem to be important factor on the cervical restoration.
- 1. Grippo JO. Abfractions: A new classification of hard tissue lesions of tooth. J Esthet Dent. 1991;3: 14-19.PubMed
- 2. Lee WC, Eakle WS. Stress-induced cervical lesions: Review of advances in the past 10 years. J Prosthet Dent. 1996;75: 487-494.ArticlePubMed
- 3. Telles D, Pegoraro LF, Pereira JC. Prevalence of noncarious cervical lesions and their relation to occlusal aspects: a clinical study. J Esthet Dent. 2000;12: 10-15.ArticlePubMed
- 4. Grippo JO. Tooth flexure (letter). J Am Dent Assoc. 1991;122: 13.
- 5. Lee WC, Eakle WS. Possible role of tensile stress in etiology of cervical erosive lesions of teeth. J Prosthet Dent. 1984;52: 374-380.PubMed
- 6. Xhonga FA. Bruxism and its effect on the teeth. J Oral Rehabil. 1977;4: 65-76.ArticlePubMed
- 7. Lambrechts P, Braem M, Vanherle G. Evaluation of clinical performance for posterior composite resins and dentin adhesives. Oper Dent. 1987;12: 53-78.PubMed
- 8. Hood JA. Experimental studies on tooth deformation: stress distribution in class V restorations. N Z Dent J. 1972;68: 116-131.PubMed
- 9. Morin DL, Douglas WH, Cross M, Delong R. Biophysical stress analysis of restored teeth: experimental strain measurement. Dent Mater. 1988;4: 41-48.ArticlePubMed
- 10. Lee CK, Park JK, Kim HC, Woo SG, Kim KH, Son K, Hur B. The influence of composite resin restoration on the stress distribution of notch shaped noncarious cervical lesion; A three dimensional finite element analysis study. J Korean Acad Conserv Dent. 2007;32: 69-79.Article
- 11. King PA. Adhesive techniques. Br Dent J. 1999;186: 321-326.ArticlePubMed
- 12. Grippo JO. Noncarious cervical lesions: the decision to ignore or restore. J Esthet Dent. 1992;4: Suppl. 55-64.ArticlePubMed
- 13. Blunck U. Improving cervical restorations: a review of materials and techniques. J Adhes Dent. 2001;3: 33-44.PubMed
- 14. Kemp-Scholte CM, Davidson CL. Complete marginal seal of class V resin composite restorations effected by increased flexibility. J Dent Res. 1990;69: 1240-1243.ArticlePubMedPDF
- 15. Kemp-Scholte CM, Davidson CL. Marginal integrity related to bond strength and strain capacity of composite resin restorative system. J Prosthet Dent. 1990;64: 658-664.PubMed
- 16. Van Meerbeek B, Peumans M, Gladys S, Braem M, Lambrechts P, Vanherle G. Three-year clinical effectiveness of four total-etch dentinal adhesive systems in cervical lesions. Quintessence Int. 1996;27: 775-784.PubMed
- 17. Rees JS. The effect of variation in occlusal loading on the development of abfraction lesions: a finite element study. J Oral Rehabil. 2002;29: 188-193.ArticlePubMed
- 18. Ichim I, Schmidlin PR, Kieser JA, Swain MV. Mechanical evaluation of cervical glass-ionomer restorations: 3D finite element study. J Dent. 2007;35: 28-35.ArticlePubMed
- 19. Lee HE, Lin CL, Wang CH, Cheng CH, Chang CH. Stresses at the cervical lesions of maxillary premolar -a finite element investigation. J Dent. 2002;30: 283-290.PubMed
- 20. Borcic J, Anic I, Smojver I, Catic A, Miletic I, Ribaric SP. 3D finite element model and cervical lesion formation in normal occlusion and in malocclusion. J Oral Rehabil. 2005;32: 504-510.ArticlePubMed
- 21. Palamara D, Palamara JE, Tyas MJ, Messer HH. Strain patterns in cervical enamel of teeth subjected to occlusal loading. Dent Mater. 2000;16: 412-419.ArticlePubMed
- 22. Katona TR, Winkler MM. Stress analysis of a bulk-filled class V light-cured composite restoration. J Dent Res. 1994;73: 1470-1477.ArticlePubMedPDF
- 23. Geramy A, Sharafoddin F. Abfraction: 3D analysis by means of the finite element method. Quintessence Int. 2003;34: 526-533.PubMed
- 24. Lindehe J, Karring T. Textbook of Clinical Periodontology. 1989;2nd edition. Copenhagen: Munksgaard; 19-69.
- 25. Schroeder HE, Page RC. Periodontal Diseases. 1990;2nd edition. Philadelphia: Lea & Fabiger; 3-52.
- 26. Le SY, Chiang HC, Huang HM, Shih YH, Chen HC, Dong DR, Lin CT. Thermo-debonding mechanisms in dentin bonding systems using finite element analysis. Biomaterials. 2001;22: 113-123.ArticlePubMed
- 27. Grippo JO, Simring M. Dental "erosion" revisited. J Am Dent Assoc. 1995;126: 619-630.ArticlePubMed
- 28. Levitch LC, Bader JD, Shugars DA, Heymann HO. Non-carious cervical lesion. J Dent. 1994;22: 195-207.PubMed
- 29. Aw TC, Lepe X, Johnson GH, Mancl L. Characteristics of non-carious cervical lesion. J Am Dent Assoc. 2002;133: 725-733.PubMed
- 30. Widmalm SE, Ericsson SG. Maximal bite force with centric and eccentric load. J Oral Rehabil. 1982;9: 445-450.ArticlePubMed
- 31. Gibbs CH, Mahan PE, Lundeen HC, Brehnan K, Walsh EK, Holbrook WB. Occlusal forces during chewing and swallowing as measured by sound transmission. J Prosthet Dent. 1981;46: 443-449.ArticlePubMed
- 32. Nakamura T, Imanishi A, Kashima H, Ohyama T, Ishigaki S. Stress analysis of metal-free polymer crowns using the three-dimensional finite element method. Int J Prosthodont. 2001;14: 401-405.PubMed
- 33. Yettram AL, Wright KW, Pickard HM. Finite element stress analysis of the crowns of normal and restored teeth. J Dent Res. 1976;55: 1004-1011.ArticlePubMedPDF
- 34. Goel VK, Khera SC, Ralston JL, Chang KH. Stresses at the dentinoenamel junction of human teeth - A finite element investigation. J Prosthet Dent. 1991;66: 451-459.ArticlePubMed
- 35. Tanaka M, Naito T, Yokota M, Kohno M. Finite element analysis of the possible mechanism of cervical lesion formation by occlusal force. J Oral Rehabil. 2003;30: 60-67.ArticlePubMedPDF
- 36. Heymann HO, Sturdevant JR, Bayne S, Wilder AD, Sluder TB, Brunson WD. Examining tooth flexure effects on cervical restorations: a two-year clinical study. J Am Dent Assoc. 1991;122: 41-47.Article
- 37. Xhonga FA, Wolcott RB, Sognnaes RF. Dental erosion II. Clinical measurements of dental erosion progress. J Am Dent Assoc. 1972;84: 577-582.Article
- 38. Heymann HO, Sturdevant JR, Brunson WD, Wilder AD, Sluder TB, Bayne SC. Twelve-month clinical study of dental adhesive in class V cervical lesions. J Am Dent Assoc. 1988;116: 179-183.PubMed
- 39. Van Meerbeek B, Peumans M, Verschueren M, Gladys S, Braem M, Lambrechts P, Vanherle G. Clinical status of ten dentin adhesive systems. J Dent Res. 1994;73: 1690-1702.ArticlePubMedPDF
- 40. Yaman SD, Sahin M, Aydin C. Finite element analysis of strength characteristics of various resin based restorative materials in class V cavities. J Oral Rehabil. 2003;30: 630-641.ArticlePubMedPDF
- 41. Leinfelder KF. Restoration of abfracted lesions. Compendium. 1994;15: 1396-1400.PubMed
- 42. Braga RR, Hilton TJ, Ferracane JL. Contraction stress of flowable composite materials and their efficacy as stress-relieving layers. J Am Dent Assoc. 2003;134: 721-728.ArticlePubMed
REFERENCES
Tables & Figures
REFERENCES
Citations
Citations to this article as recorded by 
- Impact of bonding protocols and physical-mechanical properties of composite on durability and failure rate of fixed orthodontic retainers: a systematic review of laboratory studies
Maciej Jedliński, Marta Mazur, Claudia Salerno, Katarzyna Grocholewicz, Joanna Janiszewska-Olszowska
BMC Oral Health.2025;[Epub] CrossRef - Finite element analysis of maxillary central incisors restored with various post-and-core applications
MinSeock Seo, WonJun Shon, WooCheol Lee, Hyun-Mi Yoo, Byeong-Hoon Cho, Seung-Ho Baek
Journal of Korean Academy of Conservative Dentistry.2009; 34(4): 324. CrossRef
ePub Link
Cite
XML DownloadThe influence of occlusal loads on stress distribution of cervical composite resin restorations: A three-dimensional finite element study
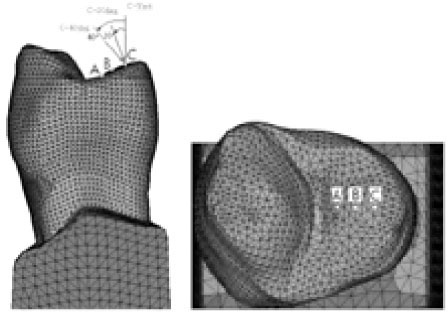
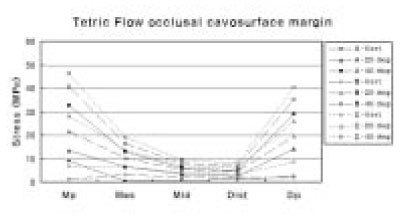
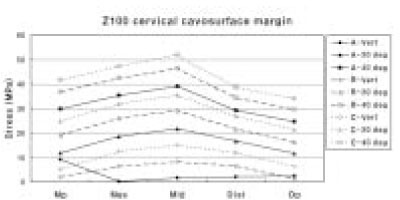
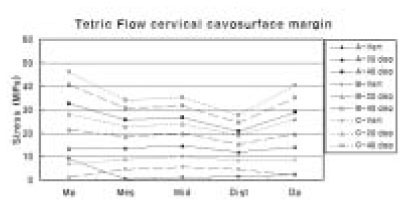
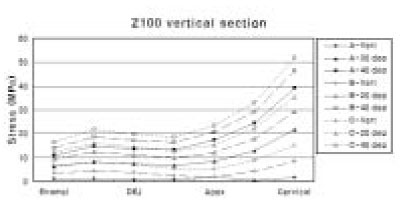
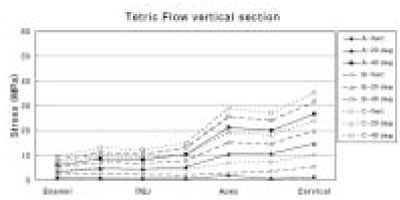
Figure 1
Disassembled 3D FE model: (a) cancellous bone, (b) cortical bone, (c) periodontal ligament, (d) dentin, (e) pulp, (f) enamel, (g) composite resin.
Figure 2
Schematic diagram of loading conditions.
Figure 3
Comparison reference nodes of buccal surface of notch-shaped lesion.
Figure 4
The maximum principal stress distribution of Z100 under various loading conditions.
Figure 5
The maximum principal stress distribution of Tetric Flow under various loading conditions.
Figure 6
The maximum principal stress distribution of occlusal cavosurface margin of Z100.
Figure 7
The maximum principal stress distribution of occlusal cavosurface margin of Tetric Flow.
Figure 8
The maximum principal stress distribution of cervical cavosurface margin of Z100.
Figure 9
The maximum principal stress distribution of cervical cavosurface margin of Tetric Flow.
Figure 10
The maximum principal stress distribution of vertical section of Z100.
Figure 11
The maximum principal stress distribution of vertical section of Tetric Flow.
Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10
Figure 11
The influence of occlusal loads on stress distribution of cervical composite resin restorations: A three-dimensional finite element study
Table 1
Mechanical properties of the tooth and supporting structures used in the study
a: Katona TR & Winkler MM b: Geramy A & Sharafoddin F
Table 2
Mechanical properties of the materials used in the study
a: Katona et al. b: Le et al.
