Articles
- Page Path
- HOME > Restor Dent Endod > Volume 38(1); 2013 > Article
- Open Lecture on Statistics Statistical notes for clinical researchers: assessing normal distribution (2) using skewness and kurtosis
- Hae-Young Kim
-
2013;38(1):-54.
DOI: https://doi.org/10.5395/rde.2013.38.1.52
Published online: February 26, 2013
Department of Dental Laboratory Science & Engineering, Korea University College of Health Science, Seoul, Korea.
- Correspondence to Hae-Young Kim, DDS, PhD. Associate Professor, Department of Dental Laboratory Science & Engineering, Korea University College of Health Science, San 1 Jeongneung 3-dong, Seongbuk-gu, Seoul, Korea 136-703. TEL, +82-2-940-2845; FAX, +82-2-909-3502, kimhaey@korea.ac.kr
©Copyights 2013. The Korean Academy of Conservative Dentistry.
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
- 65,535 Views
- 1,060 Download
- 2,551 Crossref
1) Skewness and kurtosis
2) Normality test using skewness and kurtosis
For small samples (n < 50), if absolute z-scores for either skewness or kurtosis are larger than 1.96, which corresponds with a alpha level 0.05, then reject the null hypothesis and conclude the distribution of the sample is non-normal.
For medium-sized samples (50 < n < 300), reject the null hypothesis at absolute z-value over 3.29, which corresponds with a alpha level 0.05, and conclude the distribution of the sample is non-normal.
For sample sizes greater than 300, depend on the histograms and the absolute values of skewness and kurtosis without considering z-values. Either an absolute skew value larger than 2 or an absolute kurtosis (proper) larger than 7 may be used as reference values for determining substantial non-normality.
3) How strict is the assumption of normality?
- 1. West SG, Finch JF, Curran PJ. In: Hoyle RH, editor. Structural equation models with nonnormal variables: problems and remedies. Structural equation modeling: Concepts, issues and applications. 1995. Newbery Park, CA: Sage; p. 56-75.
REFERENCES
Tables & Figures
REFERENCES
Citations

- Beyond a single sensory experience: A new approach to explore the mechanism of nature sensory experiences for pro-environmental behaviors
Hu Yu, Bin Zhou, Xueling Tan
Journal for Nature Conservation.2026; 89: 127104. CrossRef - Utilizing state workforce registries and targeted surveys to investigate workforce wellbeing
Alexandra M. Daro, Greg W. Welch, Kimberlee Belcher-Badal, Wayne Mayfield
Early Childhood Research Quarterly.2026; 74: 79. CrossRef - Effects of processing level and nutritional quality on energy intake, ingestive behaviors, palatability, and satiety in a young adult population
Alexandra B. Larcom, Ingrid E. Lofgren, Matthew J. Delmonico, Amanda Missimer, Kathleen J. Melanson
Appetite.2026; 217: 108352. CrossRef - Psychometric Properties of the Persian Version of the Strength‐Based Parenting Scale in an Adolescent Sample
Ahmad Asgarizadeh, Omid Shokri
Brain and Behavior.2025;[Epub] CrossRef - The Role of the COVID-19 Pandemic and Marginalized Identities in US Medical Students’ Burnout, Career Regret, and Medical School Experiences
Yuchen Liu, Patricia A. Frazier
Journal of Clinical Psychology in Medical Settings.2025; 32(1): 39. CrossRef - Impact of Job Insecurity on Work–Life Balance during COVID-19 in India
Asma Begum, Mathew Shafaghi, Ayesha Adeel
Vision: The Journal of Business Perspective.2025; 29(3): 353. CrossRef - Self-Leadership, Performance, and Life-Satisfaction: The Mediation Role of Flow at Work in a Three-Wave Study
Alina Daniela Ștefan, Delia Vîrgă
The Journal of Psychology.2025; 159(4): 245. CrossRef - Is the Internet to blame for problem behaviours in early adolescents? The effects of different types of Internet use, depression, and self-control
Yuanyi Mao, Bo Hu, Ki Joon Kim
Behaviour & Information Technology.2025; 44(9): 1975. CrossRef - Language proficiency and study achievement of pupils with dyslexia enrolled in content and language integrated learning (CLIL)
Chloé Parmentier, Morgane Simonis, Luk Van Mensel, Philippe Hiligsmann, Benoit Galand, Nathalie Lefèvre, Laura Ordonez Magro, Arnaud Szmalec
International Journal of Bilingual Education and Bilingualism.2025; 28(6): 645. CrossRef - A new way to conceptualize intolerance of uncertainty among adolescents: Embracing the network perspective
Haoxian Ye, Xinyu Shi, Yunyi Li, Yike Huang, Ruiyan You, Xiangting Zhang, Zhijun Yu, Huolian Li, Fang Fan
British Journal of Psychology.2025; 116(1): 89. CrossRef - The Brief Social Media Fatigue Scale (BSMFS): A New Short Version Through Exploratory Structural Equation Modeling and Associations with Trait Anxiety, Fear of Missing Out, Boredom Proneness, and Problematic Use
Palmira Faraci, Giuliana Nasonte
International Journal of Human–Computer Interaction.2025; 41(16): 10096. CrossRef - Perceived discrimination and mental health outcomes in college students: the mediating effect of preventive health behaviors and social support
Sarah C. M. Morton, Robin Everhart, Natalie Dautovich, Askar Chukmaitov
Journal of American College Health.2025; 73(6): 2380. CrossRef - Additional effect of neuromuscular electrical stimulation in a conservative intervention on morphology and strength of abductor hallucis muscle and correction of hallux valgus deformity: a randomized controlled trial
Nasrin Moulodi, Javad Sarrafzadeh, Fatemeh Azadinia, Ali Shakourirad, Maryam Jalali
Physiotherapy Theory and Practice.2025; 41(1): 44. CrossRef - The Correlation Between Fear Avoidance Beliefs and Physical Activity in Unilateral Vestibulopathies
Lien Van Laer, Hanna M. Koppelaar-van Eijsden, Ann Hallemans, Vincent Van Rompaey, Tjard R. Schermer, Tjasse D. Bruintjes, Luc Vereeck
Journal of Neurologic Physical Therapy.2025; 49(1): 24. CrossRef - Recreational awareness prevents digital game addiction associated with social exclusion in adolescents
Andaç Akçakese, Mehmet Demirel
World Leisure Journal.2025; 67(1): 54. CrossRef - The Impact of Athletic Identity, Psychological Flexibility, and Value Consistent Living on the Mental Health and Well-Being of Retired Elite Rugby Players
Jacqueline Mooney, Andrew Bethell, Chris Wagstaff, Ross White
Journal of Clinical Sport Psychology.2025; 19(3): 272. CrossRef - Does ethical climate of the organization foster entrepreneurial marketing? The role of work engagement and effective knowledge transfer
Mohammah Hossein Khasmafkan-Nezam
VINE Journal of Information and Knowledge Management Systems.2025; 55(3): 770. CrossRef - Depressive symptoms in individuals experiencing maternal overcontrol: The specific mediating role of brooding rumination
Benedetto Farina, Simone Messerotti Benvenuti, Rita B. Ardito, Federica Genova, Carola Dell'Acqua, Aurelia Lo Presti, Elena De Rossi, Giuseppe A. Carbone, Mauro Adenzato, Claudio Imperatori
Personality and Individual Differences.2025; 236: 112995. CrossRef - Reconsidering Household Food Insecurity: Assessing the Impact of Neighborhood and Household Characteristics
Sweta Tiwari, Shrinidhi Ambinakudige
Journal of Hunger & Environmental Nutrition.2025; 20(2): 251. CrossRef - Rethinking the interaction between resilience and well-being through place attachment: A case study of flood-prone urban communities in Indonesia
Bagus Takwin, Edwin de Jong, Tery Setiawan, Christina Stavrou
Journal of Urban Affairs.2025; 47(7): 2355. CrossRef - Development and validation of an electronic Symbol‐Digit Modalities Test for remote monitoring of people with multiple sclerosis
Michelangelo Dini, Giulia Gamberini, Marta Tacchini, Angela Boschetti, Alessandro Gradassi, Luca Chiveri, Mariaemma Rodegher, Giancarlo Comi, Letizia Leocani
European Journal of Neurology.2025;[Epub] CrossRef - Language Mindsets and Strategic Approaches to Studying: The Mediating Roles of Control‐Value Appraisals and Emotions
Mu‐Hsuan Chou
Psychology in the Schools.2025; 62(3): 765. CrossRef - Pilot test of JUNTOS EN PAREJA: Enhancing relationship and financial well‐being in Latine couples
Martha Yumiseva, Mariana Falconier, Zeinab Azizi
Journal of Marital and Family Therapy.2025;[Epub] CrossRef - Coach–athlete relationships, self‐confidence, and psychological wellbeing: The role of perceived and received coach support
Adam H. Coussens, Max J. Stone, Tracy C. Donachie
European Journal of Sport Science.2025;[Epub] CrossRef - Questionnaire-assessed atypical sensory sensitivity is prospectively related to higher ARFID psychopathology, higher food neophobia, and lower satisfaction with food-related life in an online sample of Chinese older adults
Yueyang Xiao, Jiayi Han, Hana F. Zickgraf, Wesley R. Barnhart, Yiqing Zhao, Jinbo He
Food Quality and Preference.2025; 122: 105303. CrossRef - How do you treat your ‘big fish’? The joint effect of perceived subordinates’ overqualification and managers’ personalities on knowledge hiding
Jiajing Hu, Yinghui Zhu, Emily (Jintao) Ma, Chen Chen
The Service Industries Journal.2025; 45(13-14): 1187. CrossRef - Sense of coherence and its components under COVID-19: relative associations with personality and psychosocial variables
Gil Zukerman, Avishai Antonovsky, Ephraim Shapiro, Liat Korn
Global Health Promotion.2025; 32(1): 107. CrossRef - How are value orientations toward intangible cultural heritage important to local cultural festival development?
Mohammad M. Alazaizeh, Paolo Mura, Malek M. Jamaliah
Journal of Heritage Tourism.2025; 20(3): 450. CrossRef - Wisdom partially mediates the relationship between spirituality and eudaimonic well-being
Ahmet Kalaycı, Ahmet Erdem, Rukiye Şahin, Douglas A MacDonald
Archive for the Psychology of Religion.2025; 47(1): 34. CrossRef - Effects of processing methods of unfermented cocoa beans from Indonesia on the chemical and physical characteristics of butter and cake
Ariza Budi Tunjung Sari, Priscilla Efraim, Xinran Song, Isabell Rothkopf, Ute Schweiggert-Weisz, Andreas Schieber, Susanne Gola
Journal of Agriculture and Food Research.2025; 19: 101563. CrossRef - The Emotion Authenticity Recognition (EAR) test: normative data of an innovative test using dynamic emotional stimuli to evaluate the ability to recognize the authenticity of emotions expressed by faces
Cristina Scarpazza, Chiara Gramegna, Cristiano Costa, Rachele Pezzetta, Maria Cristina Saetti, Alice Naomi Preti, Teresa Difonzo, Stefano Zago, Nadia Bolognini
Neurological Sciences.2025; 46(1): 133. CrossRef - Disparities in cancer-related financial toxicity across economically diverse provinces in China: A multi-center cross-sectional study
Binbin Xu, Winnie K.W. So, Kai Chow Choi, Yu Huang, Mei Liu, Lanxiang Qiu, Jianghong Tan, Hua Tao, Keli Yan, Fei Yang
Asia-Pacific Journal of Oncology Nursing.2025; 12: 100636. CrossRef - The developing mouse dopaminergic system: Cortical-subcortical shift in D1/D2 receptor balance and increasing regional differentiation
Ingvild E. Bjerke, Harry Carey, Jan G. Bjaalie, Trygve B. Leergaard, Jee Hyun Kim
Neurochemistry International.2025; 182: 105899. CrossRef - Sustainable Career Trajectories in Switzerland: The Role of Psychological Resources and Sociodemographic Characteristics
Shagini Udayar, Cecilia Toscanelli, Koorosh Massoudi
Journal of Career Assessment.2025; 33(1): 3. CrossRef - Attachment, feeling, and feeding: Associations between caregivers' attachment, emotional and feeding responsiveness, and Children's food consumption
Ana F. Santos, Carla Fernandes, Marília Fernandes, Kelly K. Bost, Manuela Veríssimo
Appetite.2025; 204: 107729. CrossRef - Transcription factors BnaC09.FUL and BnaC06.WIP2 antagonistically regulate flowering time under long-day conditions in Brassica napus
Yuanchang Min, Shuangcheng He, Xin Wang, Huan Hu, Shihao Wei, Ankang Ge, Lixi Jiang, Saiqi Yang, Yuan Guo, Zijin Liu, Mingxun Chen
Journal of Genetics and Genomics.2025; 52(5): 650. CrossRef - Understanding school staff responses to LGBTQ+ discrimination in UK secondary schools
Ben Hayes, Elizabeth Buckingham
International Journal of LGBTQ+ Youth Studies.2025; 22(4): 625. CrossRef - Evaluation of a telementalhealth alcohol use intervention program for mandated college students
Lauren Parker, Dogukan Ulupinar
Journal of Addictions & Offender Counseling.2025; 46(1): 105. CrossRef - Spelling abilities of Dutch children with developmental language disorder on words differing in complexity
Wendy Bliekendaal, Madelon van den Boer, Britt Hakvoort, Elise H. de Bree
Reading and Writing.2025; 38(7): 2087. CrossRef - Italian Grief and Meaning Reconstruction Inventory (GMRI): Exploratory, Confirmatory and Network Analyses
Paolo Soraci, Valeria Moriconi, Danilo Moggia, Francesco Maria Melchiori, Carla Di Bernardo, Luca Orati, Elisa Chini, Eleonora Guaitoli, Roberta Tiozzo, Alessandra Rossi, Sabina Spagna, Laura Abbatuccolo, Ylenia Bastianelli, Francesco Grieco, Robert A. Ne
Journal of Loss and Trauma.2025; 30(1): 58. CrossRef - Impact of Family Interaction on Future Adult Child-Parent Travel Intention: Implementing the McMaster Model of Family Functioning
Jiajing Hu, Chuchu Ou, Xiaowei Xu, Chen Chen, Xingping Cao
Journal of Travel Research.2025; 64(3): 596. CrossRef - Education moderates the association between motor involvement and executive status in ALS
Edoardo Nicolò Aiello, Barbara Poletti, Monica Consonni, Barbara Iazzolino, Silvia Torre, Veronica Faltracco, Alessandra Telesca, Francesca Palumbo, Beatrice Curti, Giulia De Luca, Eleonora Dalla Bella, Enrica Bersano, Nilo Riva, Federico Verde, Stefano M
European Journal of Neurology.2025;[Epub] CrossRef - Exploring the critical attributes of robot chef restaurants and their impact on customer perceived value: a mixed-methods study
Jinhong Gong, Xinhua Guan, Tzung-Cheng Huan
International Journal of Contemporary Hospitality Management.2025; 37(2): 522. CrossRef - Exploring learning outcomes and psycho-emotional experiences of undergraduate students in digital literacy training and support using Web-based assessment platforms
Nikolaos Pellas
Journal of Research on Technology in Education.2025; 57(4): 820. CrossRef - Women's Use of Intimate Partner Aggression: Associations With Sexist Experiences
Haley A. Miles-McLean, Christopher M. Murphy, Ana I. Maldonado
Violence Against Women.2025; 31(9): 2099. CrossRef - The Imbalance of Wanting and Liking Contributes to a Bias of Internal Attention Towards Positive Consequences of Tobacco Smoking
Domonkos File, Beáta Bőthe, Zsolt Demetrovics
International Journal of Mental Health and Addiction.2025; 23(2): 1463. CrossRef - Psychometric evaluation of the Turkish version of the Work-Related Stress Scale: A study among search and rescue workers responding to the 2023 Kahramanmaraş earthquakes
Mehmet Halil Öztürk, Ahmet Doğan Kuday
Journal of Health Psychology.2025; 30(12): 3246. CrossRef - Cognitive Profiles are Better Predictors of Literacy Attainment Than Diagnostic Outcomes in Children with High ADHD Symptoms
Sinead Rhodes, Josephine N. Booth, Emily McDougal, Jessica Oldridge, Karim Rivera-Lares, Alexia Revueltas Roux, Tracy M. Stewart
Journal of Autism and Developmental Disorders.2025; 55(9): 3257. CrossRef - The Testament Definition Scale (TDS): Normative Data from the Italian Population and Clinical Usability in Neurodegenerative Diseases
Chiara Gramegna, Valentina Bari, Edoardo Nicolò Aiello, Teresa Difonzo, Stefano Zago, Nadia Bolognini
Journal of Forensic Psychology Research and Practice.2025; 25(4): 735. CrossRef - Personality and Positive Body Image
Chee-Seng Tan, Viren Swami, Siew-May Cheng, Chin Wen Cong
Journal of Individual Differences.2025; 46(1): 17. CrossRef - Exploring the Role of Social Support and Sexual Functioning: A Study of Chemsex and Sober Sex in Men Who Have Sex with Men
Alejandro Sánchez-Ocaña, Javier Fenollar-Cortés, Sergio Fernández-Artamendi, Laura Esteban
The Journal of Sex Research.2025; 62(7): 1303. CrossRef - Clinical effectiveness of picture exchange communication system (PECS) on 5- to 7-year-old children’s oral health
A. Arafa, O. Sheiko, A. Jameel, H. A. Fansa
European Archives of Paediatric Dentistry.2025; 26(1): 191. CrossRef - Diabetes mellitus in patients with chronic bipolar disorder: prevalence, clinical correlates and relationship with homocysteine
Li Mu, Dachun Chen, Meihong Xiu, Huixia Zhou, Dongmei Wang, Xiang-Yang Zhang
International Clinical Psychopharmacology.2025; 40(2): 84. CrossRef - Picking Your Friends is a Risky Business: Psychological Impacts of Social Exclusion and Teammates Selection in a Cyberball Game with Middle School Students
Sebastiano Munini, Fabio Paglieri, Alessandro Sapienza, Mattia Negri, Marco Marini
Youth & Society.2025; 57(8): 1415. CrossRef - Enhanced adaptive permutation test with negative binomial distribution in genome-wide omics datasets
Iksoo Huh, Taesung Park
Genes & Genomics.2025; 47(1): 59. CrossRef - Time-frequency and power-law noise analyzes of three GBAS solutions of a single GNSS station
Zbigniew Siejka, Wiesław Kosek
Journal of Applied Geodesy.2025; 19(3): 533. CrossRef - Preliminary testing for affiliate stigma scale: A reliable and valid stigma measure for caregivers of women with breast cancer
Xiaofan Bu, Xi Chen, Lu Luo, Rongrong Fan, Ling Jiang, Xiangyu Liu, Doris Y.P. Leung
Asia-Pacific Journal of Oncology Nursing.2025; 12: 100652. CrossRef - Exploring Mindset Profiles and Their Associations With Enjoyment, Ideal Self, Grit, and Achievement Among Chinese Adolescent Language Learners: A Latent Profile Analysis
Liu Eerdemutu, Bai Sachurina, Junju Wang
International Journal of Applied Linguistics.2025; 35(3): 1098. CrossRef - The Bidirectional Relationship Between Sleep and Pain in Crohn’s Disease: A Daily Diary Study
Jessica K Salwen-Deremer, Sarah J Westvold, Corey A Siegel, Michael T Smith
Inflammatory Bowel Diseases.2025; 31(7): 1926. CrossRef - Does forming an implementation intention lead individuals to spontaneously use visual mental imagery?
Léonie Messmer, Fabien Fenouillet, Eve Legrand
The Journal of Social Psychology.2025; 165(2): 290. CrossRef - Unveiling the moderating effect of class problematic mobile phone use on learning burnout and state boredom: A linear mixed-effects model
Chunchun Li, Lili Qu, Yao Chen, Xiaoqin Li, Gang Cheng
Personality and Individual Differences.2025; 236: 113017. CrossRef - Toward a better understanding of environmental concern as a belief system: The lens of network psychometrics
Changjiang Tang, Duyan Yue, Wei Fu, Ziyue Hu, Xuhua Xu, Yunnan Guo, Hao Tian
Journal of Environmental Psychology.2025; 101: 102515. CrossRef - The impact of transgressing disgust-related norms in different social contexts
Michal Mikolaj Stefanczyk, Marta Kowal, Agnieszka Sorokowska
Personality and Individual Differences.2025; 233: 112937. CrossRef - Exploring movement reproduction in three-dimensional space: A comparative pilot study among people with visual impairment
Anna Rita Galiano, Sigolène Larivière, Nicolas Baltenneck, Quentin Hallez, Laura Latour
British Journal of Visual Impairment.2025; 43(2): 488. CrossRef - Turkish validity and reliability study of the Attitudes Toward Face Mask Use Scale
Özcan Erdoğan, Ahmet Doğan Kuday
Journal of Health Psychology.2025; 30(10): 2490. CrossRef - Cultivating STEM Identity and Dispositions: Using Virtual STEM Role Models in High School
Sandra J. Miles, Katherine N. Vela
Journal for STEM Education Research.2025; 8(3): 500. CrossRef - Chinese EFL learners’ basic psychological needs satisfaction and foreign language emotions: a person-centered approach
Enhao Feng, Xian Zhao, Huiyu Wang
International Review of Applied Linguistics in Language Teaching.2025; 63(1): 735. CrossRef - Need to belong and smartphone addiction risk: mediating role of anxiety symptoms and cognitive flexibility
Selin Yılmaz
Bağımlılık Dergisi.2025; 26(1): 36. CrossRef - Quantifying the Use of Space in the Clock Drawing Test: Validity in Hemispatial Neglect
Lorenzo Diana, Maria Luisa Rusconi, Edoardo Nicolò Aiello, Nadia Bolognini, Alessia Monti, Massimo Corbo, Matteo Sozzi
Archives of Clinical Neuropsychology.2025; 40(1): 102. CrossRef - Buoyancy and Achievement in Japanese Language Learning: The Serial Mediation of Emotions and Engagement
Shukun Han, Liu Eerdemutu
The Asia-Pacific Education Researcher.2025; 34(4): 1483. CrossRef - Assessing mental health professionals’ attitudes toward routine outcome monitoring across Eastern and Western cultures: an examination of invariance and latent mean differences
Zhuang She, Amanda Jensen-Doss, Hui Xu
Psychotherapy Research.2025; 35(8): 1360. CrossRef - Enhancing cash flow management in Ghanaian financial institutions through effective corporate governance practices
Leviticus Mensah, Richard Arhinful, Jerry Seth Owusu-Sarfo
Corporate Governance: The International Journal of Business in Society.2025; 25(4): 707. CrossRef - Developing design mindset: how individual and contextual factors influence the development of design mindset through method teaching
Jakob Clemen Lavrsen, Claus-Christian Carbon, Jaap Daalhuizen
Journal of Engineering Design.2025; 36(3): 325. CrossRef - Do you own Mazu’s glorious sunlight? The mediating role of psychological ownership between authentic experiences and behavioural intentions
Yung-Chuan Huang, Yi Hsien Lin
Current Issues in Tourism.2025; 28(18): 3016. CrossRef - Feasibility of EMDR toward Personality Functioning in Older Adults with PTSD
Ellen M. J. Gielkens, Sjacko Sobczak, Nienke Gerrits, Erlene Rosowsky, Lara Stas, Gina Rossi, Sebastiaan P. J. van Alphen
Clinical Gerontologist.2025; 48(1): 48. CrossRef - Turkish Version of the Psychological Responses to Grief Before Loss of Health Scale
Serap Alkaş, Sıdıka Pelit Aksu, Sultan Özkan Şat, Şengül Yaman Sözbir
Journal of Loss and Trauma.2025; 30(2): 197. CrossRef - A concentrated approach for treating OCD: a pilot study examining the feasibility and potential effectiveness of the Bergen Four Day Treatment in the U.S.
Thröstur Björgvinsson, Keith P. Klein, Cali Werner, Jennifer T. Sy, Angela Smith, Chad Brandt, Elizabeth R. McIngvale
Cognitive Behaviour Therapy.2025; 54(2): 153. CrossRef - Factors affecting preschool teachers' implementation of STEAM activities: A quantitative study in Vietnam
Manh-Tuan Nguyen, Tú Anh Hà, Huyen-Anh Mai, Kieu-Trang Thi Vu, Minh Quang Nguyễn
Social Sciences & Humanities Open.2025; 11: 101227. CrossRef - The Development of the Attachment Defenses Questionnaire (ADQ-50): A Preliminary Examination of Reliability, Validity, and Factor Structure
Emma Richardson, Alissa Beath, Simon Boag
Journal of Personality Assessment.2025; 107(1): 58. CrossRef - Authentic Experiences and Support for Sustainable Development: Applications at Two Cultural Tourism Destinations in Taiwan
Yi Hsien Lin, Yu-Lun Hsu
Leisure Sciences.2025; 47(1): 91. CrossRef - Effect of childbirth experience on the psychological well-being of postpartum women in Accra, Ghana
Emmanuel Atuesinya Azusong, Enoch Teye-Kwadjo, Kwaku Oppong Asante
Journal of Reproductive and Infant Psychology.2025; 43(5): 1175. CrossRef - Descriptive statistics for cardiothoracic surgeons: part 2 — the foundation of data interpretation
H. Shafeeq Ahmed
Indian Journal of Thoracic and Cardiovascular Surgery.2025; 41(1): 89. CrossRef - Feasibility of EMDR in Older Adults with PTSD to Reduce Frailty and Improve Quality of Life
Ellen M. J. Gielkens, Kim Turksma, Leonieke W. Kranenburg, Lara Stas, Sjacko Sobczak, Sebastiaan P. J. van Alphen, Gina Rossi
Clinical Gerontologist.2025; 48(1): 37. CrossRef - Student engagement and concerns on studies and future professions: exploratory research in a Palestinian higher education context
Vesa Korhonen, Tahani Aldahdouh, Vesna Holubek, Sanaa Abou-dagga, Nazmi Al-Masri
International Journal of Educational Management.2025; 39(3): 661. CrossRef - Health literacy and likelihood of death in community-dwelling older people
Ana Caroline Pinto Lima, Madson Alan Maximiano-Barreto, Fabiana de Souza Orlandi, Marina Aleixo Diniz Rezende, Tatiana Carvalho Reis Martins, Bruna Moretti Luchesi
Geriatric Nursing.2025; 61: 506. CrossRef - Beyond brick and mortar: determinants of retail investors’ investment intention in indirect real estate through REITs in India
G.R. Swathi, V.R. Uma
Managerial Finance.2025; 51(2): 216. CrossRef - Developing a Scale Measuring Comprehensive Sex Education Attitudes in K-12 Schools (CSEA-K12)
Sasha N. Canan, Jess C. Reich
The Journal of Sex Research.2025; 62(8): 1413. CrossRef - The double-edged sword of forensic accounting services: litigation risks in Jordan’s industrial sector
Huthaifa Al-Hazaima, Omar Arabiat, Ghassan Maayah
Journal of Financial Reporting and Accounting.2025; 23(1): 170. CrossRef - A common marker of affect recognition dysfunction in the FTD spectrum of disorders
Elisa Canu, Veronica Castelnovo, Edoardo Nicolò Aiello, Giulia De Luca, Elisa Sibilla, Fabiola Freri, Chiara Tripodi, Edoardo Gioele Spinelli, Giordano Cecchetti, Giuseppe Magnani, Francesca Caso, Paola Caroppo, Sara Prioni, Cristina Villa, Lucio Tremoliz
European Journal of Neurology.2025;[Epub] CrossRef - The Relationship Between Cumulative Ecological Risk and Problematic Smartphone Use Among Chinese College Students: Based on Latent Profile Analysis
Jinliang Guan, Wangyan Ma, Chengzhen Liu
Psychological Reports.2025; 128(3): 1542. CrossRef - The impact of professional learning and development on primary and intermediate teachers’ digital technologies knowledge and efficacy beliefs
Lynley Rose Stringer, Kerry Maree Lee, Sean Sturm, Nasser Giacaman
The Australian Educational Researcher.2025; 52(1): 315. CrossRef - Analysis of garment fit problems and body measurements of Ethiopian young female consumers
Berihun Bizuneh, Abrham Destaw, Fasika Hailu
Research Journal of Textile and Apparel.2025; 29(3): 596. CrossRef - Decisional Conflict, Patient Involvement, and the Associated Psychological Factors Relating to Mastectomy Decisions Among Women With Breast Cancer
Jing Liu, Sally Wai-Chi Chan, Dongmei Guo, Qin Lin, Sharyn Hunter, Jiemin Zhu, Regina Lai Tong Lee
Cancer Nursing.2025; 48(1): 45. CrossRef - The WOUND-Q Function and Symptoms Scales for Chronic Lower Extremity Wounds: A Validation Study
Nina Vestergaard Simonsen, Anne F. Klassen, Charlene Rae, Lily R. Mundy, Lotte Poulsen, Andrea L. Pusic, Kenneth L. Fan, Jens Ahm Sørensen
Advances in Wound Care.2025; 14(5): 238. CrossRef - Is Humor a Meaning Making Process? Investigating the Effects of Absurd Humor and Mortality Salience on Meaning in Life, Moral Identity, Belongingness, and Belief in a Just World
Joshua H. Semko, Stefan E. Schulenberg
Psychological Reports.2025; 128(3): 2000. CrossRef - Significance of Personal and Job Attributes for Managing Employee Wellbeing in the New Work from Home India
Navya Kumar, Swati Alok, Sudatta Banerjee
Vision: The Journal of Business Perspective.2025; 29(3): 339. CrossRef - From Trolling Victimization to Reactive Trolling: Moderated Mediation Effects of Online Disinhibition and Motivations
Yuanyi Mao, Bo Hu
Social Science Computer Review.2025; 43(1): 27. CrossRef - Mentalizing, epistemic trust and interpersonal problems in emotion regulation: A sequential path analysis across common mental health disorders and community control samples
Güler Beril Kumpasoğlu, Rob Saunders, Chloe Campbell, Tobias Nolte, Read Montague, Steve Pilling, Judy Leibowitz, Peter Fonagy
Journal of Affective Disorders.2025; 372: 502. CrossRef - Predicting College Students’ Preventative Behavior During a Pandemic: The Role of the Health Belief Model, Source Credibility, and Health Literacy
Ifeoluwatobi Abiodun Odunsi, Kristen Leblanc Farris
American Behavioral Scientist.2025; 69(12): 1516. CrossRef - How sport tourism experience influences daily pro-environmental behaviour: the role of eco-friendly reputation and personal norm
Rei Yamashita, Yunfan Wu, Shintaro Sato
Tourism Recreation Research.2025; 50(4): 863. CrossRef - The Relationships Between Multidimensional Schizotypy and Metacognitive Beliefs
Anchal Garg, Bruce D. Watt, Mary Rihan, Ahmed A. Moustafa
Psychological Reports.2025;[Epub] CrossRef - Racial and ethnic disparities in young adult mental health: Exploring the individual and conjoint effects of ACEs and campus climate
Minji Lee, Ana C. Uribe, Maria M. Galano
Journal of American College Health.2025; : 1. CrossRef - Validation of the uncertainty stress scale-high-risk pregnancy - Chinese brief version: Rasch analysis
Yi Jing Tsai, Chi Chen Chen, Yu Yun Hsu, Chuan Chuan Chen
BMC Pregnancy and Childbirth.2025;[Epub] CrossRef - Do European Social Funds Matter in Achieving the Sustainable Development Goals?
Roxana Maria Bădîrcea, Nicoleta Mihaela Doran, Alina Georgiana Manta, Camelia Cercel (Zamfirache)
Sustainability.2025; 17(2): 381. CrossRef - Association between fat preference and fat taste sensitivity in healthy weight and obese pregnant women based on the pre-pregnancy body mass index
Suwaibah Abd Hadi, Marina Abdul Manaf, Hafzan Haji Yusoff, Hamid Jan Jan Mohamed, Mohd Shafik Abdul Majid
Food Quality and Preference.2025; 126: 105428. CrossRef - The relationship between study resources, task performance and subjective wellbeing among university students: The role of academic self‐efficacy as personal resource
Chantal Olckers, Martha Harumavamwe
Review of Education.2025;[Epub] CrossRef - Symptom Documentation in Unstructured Palliative Care Notes of Children and Adolescents With Cancer
Katherine Bernier Carney, Jacob Wilkes, Tumilara Aderibigbe, Kristin Stegenga, Holly Spraker-Perlman, Lauri A. Linder
Journal of Pain and Symptom Management.2025; 69(4): 409. CrossRef - Satisfaction with learning materials in relation to volitional competence and behavioral intention in open and flexible learning environments
Mesut Aydemir, Munevver Başman, Yusuf Zafer Can Uğurhan, Nazire Burçin Hamutoğlu
Distance Education.2025; : 1. CrossRef - Energy storage and transmission line design for an island system with renewable power
Arya Sevgen Misic, Mumtaz Karatas, Abdullah Dasci
Computers & Industrial Engineering.2025; 201: 110901. CrossRef - Regional economic level moderates the impact of patients' and family carers’ cancer-related work changes and hospital level on financial toxicity in China: A multi-centre cross-sectional study
Binbin Xu, Winnie K.W. So, Kai Chow Choi
European Journal of Oncology Nursing.2025; 74: 102782. CrossRef - A Multi- Mediation Analysis on the Impact of Social Media and Internet Addiction on University and High School Students’ Mental Health Through Social Capital and Mindfulness
Girum Tareke Zewude, Tarikuwa Natnael, Getachew Tassew Woreta, Anmut Endalkachew Bezie
International Journal of Environmental Research and Public Health.2025; 22(1): 57. CrossRef - The relationship between physical activity and career decision-making self-efficacy in Chinese college students: the mediating roles of self-control and social anxiety
Yuan Fang, Tingting Xu, Maosheng Ye, Changquan Li
Frontiers in Psychology.2025;[Epub] CrossRef - Experiential avoidance, depression, and difficulty identifying emotions in social network site addiction among Chinese university students: a moderated mediation model
Jiale Wang, Ning Wang, Yang Liu, Zirui Zhou
Behaviour & Information Technology.2025; : 1. CrossRef - Fear of Missing out and Online Social Anxiety in University Students: Mediation by Irrational Procrastination and Media Multitasking
Weimiao Wu, Jie Zhang, Namjeong Jo
Behavioral Sciences.2025; 15(1): 84. CrossRef - Analysis of the visual degradation of PV modules installed in different climatic zones in India
Dinesh Yadav, Amit Kumar Saraf
Environment, Development and Sustainability.2025;[Epub] CrossRef - Evaluation of Hearing Thresholds in Infants With Autism Spectrum Disorder Using Auditory Brainstem and Steady-State Responses
Dimitra Chaldi, Konstantinos Mourtzouchos, Spyridon Lygeros, Gerasimos Danielides, Stefanos Naxakis
Cureus.2025;[Epub] CrossRef - Child–Family Interactions from the Eyes of Children
Özlem Dönmez, Ozana Ural
International Journal of Early Childhood.2025; 57(2): 425. CrossRef - Using inquiry-based learning approach in the teaching process of divisibility rules
Bedirhan Teke, Hamza Çalışıcı
Asia Pacific Education Review.2025; 26(2): 519. CrossRef - Judgment of Learning in a Motor Task
Athanasia Chatzipanteli, Aglaia Zafeiroudi, Alexandros Fotiadis, Charalampos Krommidas
Journal of Teaching in Physical Education.2025; : 1. CrossRef - A Machine‐Learning Approach to Understanding Performance of Canadian Nonprofit Sport Organizations
Yanxiang Yang, Terri Byers, Joerg Koenigstorfer
Nonprofit Management and Leadership.2025; 35(3): 663. CrossRef - Cognitive‐Behavioral Intervention for Children With Hematological Cancer Receiving Chemotherapy: A Randomized Controlled Trial
Tenaw Gualu Melesse, William Ho Cheung Li, Janita Pak Chun Chau, Mulugeta Ayalew Yimer, Abdulkadir Mohamedsaid Gidey, Sewbesew Yitayih
Psycho-Oncology.2025;[Epub] CrossRef - Physical and emotional abuse with internet addiction and anxiety as a mediator and physical activity as a moderator
Jinyin Peng, Yang Liu, Xubo Wang, Zhenxiu Yi, Lei Xu, Fulan Zhang
Scientific Reports.2025;[Epub] CrossRef - Social comparison and aggression in mainland Chinese adolescents: testing the mediating role of self-control
Yaping Wang, Yanchun Liu, Huan Wang, Ruolan Li
Current Psychology.2025; 44(3): 1631. CrossRef - Teachers' AI readiness in Chinese as a Foreign Language education: Scale development and validation
Nuoen Li, Yu Liang
System.2025; 129: 103597. CrossRef - Prevalence and Risk Factors for Leg Length Discrepancy in Children With Idiopathic Clubfoot Treated With Ponseti Method
Claire Schaibley, Beltran Torres-izquierdo, Rohit Siddabattula, Pooya Hosseinzadeh
Journal of Pediatric Orthopaedics.2025; 45(4): 234. CrossRef - Lack of mental integration and emotion dysregulation as a possible long-term effect of dysfunctional parenting: An EEG study of functional connectivity before and after the exposure to attachment-related stimuli
Giuseppe A. Carbone, Benedetto Farina, Aurelia Lo Presti, Mauro Adenzato, Claudio Imperatori, Rita B. Ardito
Journal of Affective Disorders.2025; 375: 222. CrossRef - Assessment of psychological health effects of nurses during 2022–2023 of the COVID-19 pandemic: a descriptive study in Southern Taiwan
Hui-Ru Lin, Yung-Kuo Lee, Chen-Lin Chang, Ching-Hui Kuo, Hsin-Yun Ho, Chi-Jen Wu, Yi-Qian Chen, Cheng-Chun Wu, Yu-Cheng Ho, Tian-Huei Chu, Cheng-Hsin Chuang, Chou-Yuan Ko
Annals of Medicine.2025;[Epub] CrossRef - A deep learning framework for automatic assessment of presence in virtual reality using multimodal behavioral cues
Peerawat Pannattee, Shogo Shimada, Vibol Yem, Nobuyuki Nishiuchi
Neural Computing and Applications.2025; 37(8): 6283. CrossRef - Development and validation of the gift reciprocation anxiety scale (GRAS) for youths and adults in intimate relationships
Mohd. Ashik Shahrier, Shakira Khatun
Heliyon.2025; 11(2): e41956. CrossRef - Deciphering the Link Between Diagnosis-Related Group Weight and Nursing Care Complexity in Hospitalized Children: An Observational Study
Manuele Cesare, Fabio D’Agostino, Emanuele Sebastiani, Gianfranco Damiani, Antonello Cocchieri
Children.2025; 12(1): 103. CrossRef - Leading by example: Experimental evidence that therapist lived experience disclosures can model the path to recovery for clients
Alysia M. Robertson, Tegan Cruwys, Mark Stevens, Michael J. Platow
British Journal of Psychology.2025; 116(2): 409. CrossRef - Exploring the psychological outcomes of cancer diagnosis on parental role and parent–child relationships: validation of the Italian Parenting Concerns Questionnaire (PCQ)
Alessandra Babore, Carmen Trumello, Sonia M. Bramanti, Tânia Brandão
Current Psychology.2025; 44(3): 1832. CrossRef - Understanding music teachers’ formative assessment intention and implementation: A Chinese Mainland context
Le-Xuan Zhang, Zi Yan, Xiang Wang
International Journal of Music Education.2025;[Epub] CrossRef - Validity and reliability of the breast cancer comfort assessment scale in palliative care
Rahime Yöntem Ölmez, İlgün Özen Çınar
International Journal of Assessment Tools in Education.2025; 12(1): 33. CrossRef - The impact of eating behavior on destination choice: The case of vegetarianism
Pınar Yeşilçimen, H. Bahadır Akın
Journal of Multidisciplinary Academic Tourism.2025; 10(1): 35. CrossRef - Basic Statistics for Radiologists: Part 1—Basic Data Interpretation and Inferential Statistics
Adarsh Anil Kumar, Jineesh Valakkada, Anoop Ayyappan, Santhosh Kannath
Indian Journal of Radiology and Imaging.2025; 35(S 01): S58. CrossRef - The Relationship Between Empirical Avoidance, Anxiety, Difficulty Describing Feelings and Internet Addiction Among College Students: A Moderated Mediation Model
Zhenxiu Yi, Wenqian Wang, Ning Wang, Yang Liu
The Journal of Genetic Psychology.2025; 186(4): 288. CrossRef - Does smart technology, artificial intelligence, robotics, and algorithm (STARA) awareness have a double-edged-sword influence on proactive customer service performance? Effects of work engagement and employee resilience
Hsiu-Yu Teng, Ming-Way Li, Chien-Yu Chen
Journal of Hospitality Marketing & Management.2025; 34(3): 443. CrossRef - Childhood heart disease and parental emotional wellbeing: a predictive model to explain the perception of quality of life in children and adolescents
Teresa Grimaldi Capitello, Cinzia Correale, Giulia Amodeo, Michela Balsamo, Leonardo Carlucci, Caterina Fiorilli
Health and Quality of Life Outcomes.2025;[Epub] CrossRef - Value of Enterprise Risk Management Integration and Supply Chain Performance: Mediating Role of Firm’s Resilience Capability
Dawud Jidda Jidda, Li Zhen, Sheikh Farhan Ashraf, Aemin Nasir, Timothy Amoako
Sage Open.2025;[Epub] CrossRef - Work–Family Interface and Subjective Career Success: The Role(s) of Job Crafting as a Personal Resource
Eileen Koekemoer, Chantal Olckers
Journal of Career Development.2025; 52(2): 236. CrossRef - A data-driven approach to study temporal characteristics of COVID-19 infection and death Time Series for twelve countries across six continents
Sabyasachi Guharay
BMC Medical Research Methodology.2025;[Epub] CrossRef - Predicting academic procrastination in online courses: The role of external locus of control and other mediator variables
Murat Çınar, Dilek Doğan, Ömer Demir
Education and Information Technologies.2025; 30(9): 11751. CrossRef - Okul Öncesi Dönemdeki 4-6 Yaş Grubu Çocukların Duygu Düzenleme Becerisinin Sosyal Yetkinlik ile İlişkisinde Cinsiyet ve Yaşın Düzenleyici Rolü
Nurhan Can, Handan Doğan
Temel Eğitim Araştırmaları Dergisi.2025; 5(1): 33. CrossRef - Oncofertility Barriers in Nurses Caring for Women with Breast Cancer
Li Hu, Chaoting Zheng, Binbin Xu, Wei Tang, Hong Li
Scientific Reports.2025;[Epub] CrossRef - İş Yeri Nezaketsizliğinin İşe Tutkunluğa Etkisinde Örgütsel Sinizmin Aracılık Rolü
Selen Doğan, Emel Aktuğ
Alanya Akademik Bakış.2025; 9(2): 565. CrossRef - A Latent Profile Analysis of Cyber Dating Abuse Among College Students: Associations With Maladaptive Personality Traits, Negative Emotionality, and Impulsivity
Ariana Cervantes, Genevieve M. Jessen, Theodore V. Cooper, Mitchell Kirwan
Journal of Interpersonal Violence.2025;[Epub] CrossRef - Goals of older adults transitioning from hospital to home in the community
Melody Maximos, Briana Virag, Alicia Page, Vanina Dal Bello-Haas
Disability and Rehabilitation.2025; : 1. CrossRef - Examining the reciprocal associations of muscularity bias internalization with muscularity-oriented disordered eating, muscle dysmorphia symptoms, and eating-related psychosocial impairment in Chinese adults
Jinbo He, Lanting Cheng, Shuqi Cui, Shijia Wu, Zexuan Jiang, Jason M. Nagata
Body Image.2025; 53: 101862. CrossRef - Anxiety and inhibitory control play a chain mediating role between compassion fatigue and Internet addiction disorder among nursing staff
Xinxin Tan, Zhongzheng Li, Hong Peng, Min Tian, Jiong Zhou, Ping Tian, Jingrui Wen, Shenglin Luo, Yan Li, Ping Li, Yang Liu
Scientific Reports.2025;[Epub] CrossRef - Transformational leadership in social work organizations: Associations with job autonomy, professional commitment, and turnover intentions among Chinese social workers
Ziyu Liu
The British Journal of Social Work.2025;[Epub] CrossRef - Prevalence and accuracy of nursing diagnoses in patients with malignant bronchial and lung cancer: A retrospective observational study
Manuele Cesare, Erasmo Magliozzi, Fabio D’Agostino, Valentina Zeffiro, Antonello Cocchieri
European Journal of Oncology Nursing.2025; 77: 102931. CrossRef - Physics-informed neural networks for monitoring dynamic systems: ring bearing system study case
Josafat Leal Filho, Matheus Wagner, Antônio Augusto Fröhlich
Design Automation for Embedded Systems.2025;[Epub] CrossRef - Social and Emotional Competencies of Children with Autism Spectrum Disorder and/or Intellectual Disability
Anamarija Žic Ralić, Sara Bubalo, Marijana Vrankić Pavon
Journal of Autism and Developmental Disorders.2025;[Epub] CrossRef - Effect of multiple social norms on physicians’ use of clinical practice guidelines on antimicrobials: A structural equation modeling approach
Lingjie Wang, Qiwen Song, Shiyin Wu, Wenbin Liu
Research in Social and Administrative Pharmacy.2025; 21(11): 872. CrossRef - The Implementation of a Blended Counseling Intervention in Undergraduate Engineering Students: The Effect on Mental Health
Antonios Kalamatianos, Kalliope Kounenou, Christos Pezirkianidis
Healthcare.2025; 13(5): 511. CrossRef - Mapping love: a personality-centered network analysis of relationship satisfaction
Oliver Tobias Schulz, Danièle Anne Gubler, Ursina Elsa Raemy, Stefan Johannes Troche
Frontiers in Psychology.2025;[Epub] CrossRef - Genetic protection from type 1 diabetes resulting from accelerated insulin mRNA decay
René van Tienhoven, Denis O’Meally, Tristan A. Scott, Kevin V. Morris, John C. Williams, John S. Kaddis, Arnaud Zaldumbide, Bart O. Roep
Cell.2025; 188(9): 2407. CrossRef - Work-to-leisure spillover and job burnout among frontline employees in Taiwan tourism and hospitality industries: The moderating role of job autonomy
Chin-Sheng Chen, Shih-Hao Liu, Chin-Hsiang Tsai, Shou-Guan Wu
Human Systems Management.2025; 44(4): 710. CrossRef - Linking social undermining to cyberloafing: cross-sectional and cross-lagged panel investigations
Omer Farooq Malik, Irum Bhatti, Kawsu Sillah
Cogent Business & Management.2025;[Epub] CrossRef - The Role of Legislation in Developing and Advancing Women in the South African Workplace
Gaelle Fitong Ketchiwou
African Journal of Employee Relations.2025;[Epub] CrossRef - Walking into aging: real-world mobility patterns and digital benchmarks from the InCHIANTI Study
Jose Albites-Sanabria, Pierpaolo Palumbo, Stefania Bandinelli, Ilaria D’Ascanio, Sabato Mellone, Anisoara Paraschiv-Ionescu, Arne Küderle, Andrea Cereatti, Silvia Del Din, Felix Kluge, Eran Gazit, Carl-Philipp Jansen, Laura Delgado-Ortiz, Judith Garcia-Ay
npj Aging.2025;[Epub] CrossRef - Mapping teacher wellbeing in Slovakia: insights into resilience, relationships, and support needs
Lenka Janik Blaskova, Liz Winter
Frontiers in Education.2025;[Epub] CrossRef - Psychological resilience and valued living as mediators in the relation between moral injury and attitudes toward future among Turkish adults
Feyza Topçu
BMC Psychology.2025;[Epub] CrossRef - Fostering Academic Writing Skills in Tourism and Hospitality Students: Insights from a Teaching Intervention
Mary Eddy, Jeremy Phillips, Gabriella Cheang, Jose But
Journal of Hospitality & Tourism Education.2025; : 1. CrossRef - Exploring longitudinal associations between thinness- and muscularity-oriented eating and body image disturbances in Chinese adult women and men
Yueyang Xiao, Wesley R. Barnhart, Shijia Wu, Zexuan Jiang, Jason M. Nagata, Jinbo He
Body Image.2025; 54: 101933. CrossRef - The effect of age and fluid intelligence on working memory in different modalities among elderly individuals: a moderated mediation analysis
Eyal Heled, Ohad Levi
Aging, Neuropsychology, and Cognition.2025; 32(5): 709. CrossRef - Psychosocial predictors of problem gambling severity in males: findings from a longitudinal study of Australian men
Vincent O. Mancini
International Gambling Studies.2025; 25(1): 168. CrossRef - Within-Family Association between Intimate Partner Violence Victimization and Coparenting Support Spanning the First 9 Years of Child Life: A Dyadic, Cross-Lagged Approach
Jinhui Qiao, Nan Zhou, Hongjian Cao
Journal of Family Violence.2025;[Epub] CrossRef - A longitudinal study investigating the association between social maturity, social preference and children’s perceptions of their playfulness
Rianne L. van de Weitgraven, Brenda R. J. Jansen, Tycho J. Dekkers, Elian Fink
Scientific Reports.2025;[Epub] CrossRef - The Role of Negative Symptoms on the Continuum of Psychosis Risk as a Mediator of the Relationship Between Personality and Functioning in Individuals With Psychotic‐Like Experiences
Dawid Kruk, Łukasz Gawęda, Aleksandra Arciszewska‐Leszczuk, Aneta Kalisz, Piotr Błądziński, Dorota Frydecka, Andrzej Cechnicki
Early Intervention in Psychiatry.2025;[Epub] CrossRef - Effects of impulsivity and emotions on time perception: Laboratory behavioral measures
Diana Moreira, Andreia Azeredo, Ângela Leite, Fernando Barbosa
Perception.2025; 54(4): 239. CrossRef - The effect of supply chain risks management practices on operational performance of pharmaceutical manufacturing companies in Addis Ababa, Ethiopia: Analytical cross-sectional study
Dinku Mechal, Bekele Boche, João Zambujal-Oliveira
PLOS One.2025; 20(5): e0321311. CrossRef - Discounting seems the most toxic dimension of invalidation in fibromyalgia: a cross-sectional analysis
Heidi Willemse, Johanna E. Vriezekolk, Rinie Geenen
Rheumatology International.2025;[Epub] CrossRef - Maternal Emotion Regulation and Parenting: A Physiological Perspective
Frances H. Li, Nicole M. Froidevaux, Margaret L. Kerr, Patricia A. Smiley, Paul D. Hastings, Jessica L. Borelli
Developmental Psychobiology.2025;[Epub] CrossRef - Modulation of motor unit recruitment threshold and common synaptic inputs in triceps surae muscles: effects of ankle position
Xin Sienna Yu, Jackson T. Levine, José L. Pons
Journal of Applied Physiology.2025; 138(6): 1638. CrossRef - Adult Insecure Attachment Styles, Neuroticism, and Dating Relationship Quality
Jeffrey B. Jackson, Flor Yousefian Tehrani, Dean M. Busby, Luca Codecà
Contemporary Family Therapy.2025;[Epub] CrossRef - Life’s Purpose and Social Support: Keys To Promote Cognitive Functioning of Middle-aged Adults in Pakistan
Tehreem Sarfraz, Tehreem Arshad
Ageing International.2025;[Epub] CrossRef - Multidimensional Scale of Motives for Postponing Parenthood (MSMPP-18): Development, factorial structure and psychometric properties
Małgorzata Szcześniak, Adam Falewicz, Daria Brodowska
Scientific Reports.2025;[Epub] CrossRef - Indirect effects of parental and peer attachment on Internet Gaming Disorder among adolescents: The role of negative automatic thoughts
Iulia Maria Coșa, Anca Dobrean, Robert Balazsi, Costina-Ruxandra Poetar
Personality and Individual Differences.2025; 241: 113193. CrossRef - Ketone monoester ingestion improves cardiac function in adults with type 2 diabetes: a double-blind, placebo-controlled, randomized, crossover trial
M. Perissiou, Z. L. Saynor, K. Feka, C. Edwards, T. J. James, J. Corbett, H. Mayes, J. Shute, M. Cummings, M. I. Black, W. D. Strain, J. P. Little, A. I. Shepherd
Journal of Applied Physiology.2025; 138(2): 546. CrossRef - Power-Law Noise Analysis of the Vertical GNSS Station Coordinates in Europe
Paweł Postek, Wiesław Kosek, Kamil Maciuk
IEEE Geoscience and Remote Sensing Letters.2025; 22: 1. CrossRef - Self-Concept Modulates Motivation and Learning Strategies in Higher Education: Comparison According to Sex
Ramón Chacón-Cuberos, Jennifer Serrano-García, Inmaculada Serrano-García, Manuel Castro-Sánchez
Education Sciences.2025; 15(7): 873. CrossRef - The longitudinal effects of parental academic conditional regard on basic psychological need satisfaction among adolescents: Testing the indirect role of mindfulness
Yonghe Ti, Cong Yi, Jun Wei, Shun-Lam Chan
Children and Youth Services Review.2025; 176: 108436. CrossRef - The influence of leadership on work engagement mediated by job crafting
Petronella Jonck, Tsholofelo Manamela
SA Journal of Human Resource Management.2025;[Epub] CrossRef - The influencing factors of turnover intention among pediatric healthcare workers: a moderated mediation model
Qingwen Jia, Wenkang Shi, Hao Yuan
Human Resources for Health.2025;[Epub] CrossRef - Family history does not influence stress or major coping styles in adults with neurofibromatosis type 1
Mikaela Bradley, Ashley Cannon, Bryce Brown, Kelly Taylor, Paul Moots, Emily McQuillen
Journal of Genetic Counseling.2025;[Epub] CrossRef - The assessment of job insecurity: Dimensionality, reliability, and validity of the Multidimensional Job Insecurity Questionnaire – Revised (MJIQ-R)
Antonio Chirumbolo, Antonino Callea, Flavio Urbini
Economic and Industrial Democracy.2025; 46(3): 742. CrossRef - Premenopausal and perimenopausal predictors of postmenopausal health and well‐being: Testing a disposition‐belief‐motivation framework
Olivia Godfrey, Tim Bogg
Applied Psychology: Health and Well-Being.2025;[Epub] CrossRef - Simple method for predicting the distraction due to speech and babble
Valtteri Hongisto, Reijo Alakoivu, Jukka Keränen, Johann Laukka
Building and Environment.2025; 276: 112915. CrossRef - Effects of Internal and External Cues on Brain Activity and Gait in Parkinson’s Disease: Findings From BARC-PD
Rodrigo Vitorio, Rosie Morris, Lisa Graham, Julia Das, Richard Walker, Claire McDonald, Martina Mancini, Samuel Stuart
Neurorehabilitation and Neural Repair.2025; 39(10): 826. CrossRef -
Flexural Testing on
Dendrocalamus
Bamboo in Thailand: Mechanical Properties, Structural Performance, and Engineering Applications
Worathep Sae-Long, Thanakorn Chompoorat, Suchart Limkatanyu, Nattapong Damrongwiriyanupap, Piti Sukontasukkul, Pannipa Chaowana, Kitti Chaowana, Tanan Chub-Uppakarn
Journal of Materials in Civil Engineering.2025;[Epub] CrossRef - Decoders are Less Efficient in RAN Objects than Children using Lexical Processing
Margot Fromont, Jolijn Vanderauwera, Marie Van Reybroeck
Developmental Neuropsychology.2025; : 1. CrossRef - Prospective Teachers' Self‐Efficacies in Project Development: Scale Development and Review by Variables
Zübeyde ER, Perihan DİNÇ ARTUT, Ayten Pınar BAL
Psychology in the Schools.2025; 62(10): 3892. CrossRef - AI-driven insights into urban agriculture: Using youtube data to promote social resilience and self-sufficiency
Mahsa Tarashkar, Akbar Rahimi, Salman Qureshi
Sustainable Cities and Society.2025; 123: 106275. CrossRef - Co-development of career adaptability and academic self-efficacy in college: A four-wave investigation
Cong Yi, Yonghe Ti, Yanyan Liu, Yisi Zhan, Jun Wei
Journal of Applied Developmental Psychology.2025; 98: 101792. CrossRef - Sex differences in the prevalence and clinical correlates of autistic features in patients with chronic schizophrenia: a large scale cross-sectional study
Qihui Guo, Rongrong Zhu, Zheng Ma, Ying He, Dongmei Wang, Xiangyang Zhang
International Journal of Psychiatry in Clinical Practice.2025; 29(1): 9. CrossRef - Psychometric properties of the Warwick Edinburgh Mental Well-being Scale: a systematic review
B. P. R. Perera, A. R. Wickremasinghe, T. A. P. De Za
Systematic Reviews.2025;[Epub] CrossRef - Associations Between Parenting Practices and Peer Pressure Among Adolescents: The Mediating Role of Autonomy and Relatedness
M. A. Crespo-López, I. M. Koning
Journal of Prevention.2025;[Epub] CrossRef - Evaluating a Mobile Health Intervention (GUIDE App) for First Responders, Military Personnel, and Veterans: Randomized Controlled Trial
Morgan K Dunphy, Heather J Nuske
Journal of Medical Internet Research.2025; 27: e71155. CrossRef - Convergence and equating norms between the Telephone Interview for Cognitive Status (TICS), the MMSE and the MoCA in an Italian population sample
Edoardo Nicolò Aiello, Beatrice Curti, Giulia De Luca, Sara Casartelli, Lorenzo Esposti, Chiara Curatoli, Alice Zanin, Elisa Camporeale, Martina Andrea Sirtori, Federico Verde, Vincenzo Silani, Nicola Ticozzi, Nadia Bolognini, Barbara Poletti
Aging Clinical and Experimental Research.2025;[Epub] CrossRef - Analyzing the Interaction of Industry 4.0 and Sustainable Global Marketing Channel Development with Necessary Condition Analysis: The Role of Inter-Organizational Trust
Matti Haverila, Jenny Carita Twyford, Hadi Zarea
Sustainability.2025; 17(6): 2489. CrossRef - Give me Support and Hope, and I Can Be Creative: Evidence for a Mediation Model from Five Countries
Chee-Seng Tan, Jonathan E. Ramsay, Sanju George, Argel Bondoc Masanda, Soon-Aun Tan, Jing Zhang, Siew-May Cheng, Mark A. Runco, Walton Wider
Applied Research in Quality of Life.2025; 20(4): 1469. CrossRef - Greater tolerance of uncertainty facilitates thriving in doctors entering postgraduate training
Russell Peek, Rachel Arnold, Lee Moore
BMC Medical Education.2025;[Epub] CrossRef - Psychometric Validation of the FACE‐Q Dental Module in Patients With Malocclusions
Ali Tassi, Anne F. Klassen, Jessica Li, Karen W. Y. Wong Riff, Charlene Rae
Community Dentistry and Oral Epidemiology.2025; 53(4): 442. CrossRef - The Associations Between Computational Thinking and Learning to Play Musical Instruments
Tami Regev Cohen, Bar Armon, Arnon Hershkovitz
Education Sciences.2025; 15(3): 306. CrossRef - Longitudinal associations between authentic inner compass and depressive symptoms among college students: A latent curve model with structured residuals
Xiting Zhou, Yonghe Ti, Jun Wei, Tiran Li
Personality and Individual Differences.2025; 239: 113118. CrossRef - Assessing the Alignment Between the Humpty Dumpty Fall Scale and Fall Risk Nursing Diagnosis in Pediatric Patients: A Retrospective ROC Curve Analysis
Manuele Cesare, Fabio D’Agostino, Deborah Hill-Rodriguez, Danielle Altares Sarik, Antonello Cocchieri
Healthcare.2025; 13(14): 1748. CrossRef - Impacts of green curriculum exposure and sustainability awareness on green entrepreneurship intention among Malaysian university students: The mediating role of self-efficacy
Chan Man Seong, Tan Chi Hau, Thee Chun Cheng, Tan Booi Chen
Industry and Higher Education.2025; 39(4): 379. CrossRef - Co-curricular engagement, moral quotient, and pro-environmental behaviors of university students in Bangladesh
Mohd. Ashik Shahrier, Kazi Imrul Kayesh, Atik Mahomud Zubaier, Rawshan Ara Khan, Nahida Sarkar, Md. Luthfor Rahman
BMC Psychology.2025;[Epub] CrossRef - Validity and Reliability of the Dental Neglect Scale in German
Katharina Marilena Weil, Theresa Marie Weßlau, Laura Agnes Ingrid Magerfleisch, Hannah Tröger, Lisa Irmscher, David Bantel, Clara Theres Meyer-Probst, Katja Petrowski, Hendrik Berth
Dentistry Journal.2025; 13(5): 225. CrossRef - Community built environment attributes moderate the relationship between family support and depression among older adults in urban China
Qian Sun, Yingqi Guo, Yanlong Yin, Youwei Wang, Nan Lu
BMC Geriatrics.2025;[Epub] CrossRef - Profiles of Learning-Related Motivational Beliefs and Perceived Effectiveness of Learning Strategies Related to Academic Achievement and Psychological Well-Being
Eliis Härma, Aleksander Pulver, Eve Kikas
European Journal of Psychology and Educational Research.2025; 8(1): 17. CrossRef - The Effect of Work Environment and Work‐Related Characteristics on Perceived Individual Work Performance of Front‐Line Nurse Managers: A Cross‐Sectional Study
Tuğba Yeşilyurt Sevim, Emine Türkmen, Nilgün Göktepe, Nuray Erdemir Çakmak, Eda Özlem Ünal, Esra Adigüzel, Ramiz İşçi
Research in Nursing & Health.2025; 48(4): 441. CrossRef - The mediating role of self-regulated learning strategies in the intelligence and academic achievement Nexus
V.M. Shamla, C. Jayan
Social Sciences & Humanities Open.2025; 11: 101569. CrossRef - Ensemble machine learning and tree-structured Parzen estimator to predict early-stage pancreatic cancer
Kah Keng Wong
Biomedical Signal Processing and Control.2025; 108: 107867. CrossRef - Relationship between ruminative dispositions and perceived sports performance in young elite athletes in Hong Kong: the role of problem-oriented coping strategies
Dong-Tai Chen, Jui-Ti Nien, Xiaoling Geng, Jeffrey Yu, Chatkamon Singhnoy, Yu-Kai Chang
Frontiers in Sports and Active Living.2025;[Epub] CrossRef - Distinct Empathy Profiles in Autism and Social Anxiety: A Comparative Study
Sigal Tikochinsky, Esther Ben‐Itzchak, Gil Zukerman
Autism Research.2025; 18(8): 1620. CrossRef - Evaluating the predictive accuracy of some regression models and artificial neural networks in streamflow forecasting (a case study of the Kaduna River, Northwest Nigeria)
Lawal Mamudu, Ali Aldrees, Salisu Dan’azumi, Alhassan Yahaya
Modeling Earth Systems and Environment.2025;[Epub] CrossRef - The Relationship Between Intolerance of Uncertainty and Alcohol Use in First Responders: A Cross-Sectional Study of the Direct, Mediating and Moderating Role of Generalized Resistance Resources
Tyrone B. Pretorius, Anita Padmanabhanunni
International Journal of Environmental Research and Public Health.2025; 22(3): 383. CrossRef - Redesigned final year research program for undergraduate nursing students: A mixed-methods study
Jamie Qiao Xin Ng, Jing Shi Chua, Wei How Darryl Ang, Lydia Siew Tiang Lau, Jessica Raffaella Pereira, Emily Neo Kim Ang, Annelissa Mien Chew Chin, Kim Kee Toh, Suei Nee Wong, Liang Shen, Joelle Yan Xin Chua, Yong Shian Shawn Goh, Shefaly Shorey
Nurse Education Today.2025; 147: 106620. CrossRef - Relationship Between Self-Determination and IEP Goal Attainment for Autistic Adolescents
Delia D. D. Kan, Kara A. Hume, Karrie A. Shogren, Brianne Tomaszewski, Jian Ming Ng
Career Development and Transition for Exceptional Individuals.2025;[Epub] CrossRef - Normative data and objective benchmarks for selected force plate tests for professional and youth soccer players in the English Football League
Andrew J. Badby, Paul Comfort, Nicholas J. Ripley, Peter D. Mundy, Marcos A. Soriano, Francisco J. Robles-Palazón, Jack Fahey, Paul Sindall, Christopher Bramah, John J. McMahon
Journal of Sports Sciences.2025; 43(20): 2306. CrossRef - Associations Among Depressive and Anxious Symptoms, Fear of Missing Out, and Problematic Smartphone Use Severity Among Chinese Adolescents: A Three-Wave Random-Intercept Cross-Lagged Panel Analysis
Guangzhe Yuan, Caimeng Liu, Wei Shi, Xu Ding
Psychology Research and Behavior Management.2025; Volume 18: 1347. CrossRef - Doğal bal tüketiminde tüketici algıları: Demografik faktörlerin etkisi
Fatih Bilici
Tarım Ekonomisi Dergisi.2025; 31(1): 173. CrossRef - Pornographic Media Use and Mental Health Problems in a Large Nationally Representative Sample of Chinese Adolescents: The Moderating Effect of Sexual Knowledge and Its Sources
Jiatong Xu, Lijun Zheng
Sexuality Research and Social Policy.2025; 22(4): 2209. CrossRef - Does the pursuit of perfection by Chinese people harm interpersonal relationships? Evidence from the Wenjuan
Jun Zhang, Xiaoyan Luo, Wanshu Yang, Jie Xu, Ping Deng, Hui Wu, Junqiao Guo
Frontiers in Psychology.2025;[Epub] CrossRef - Correlation between obesity-related indices and hyperuricemia among the elderly population in China: A cross-sectional study
Jian Li, Junbo Liu, Zhongyi Liu, Weining Xie
Medicine.2025; 104(15): e42112. CrossRef - Parental Language and Literacy and Not the Home Literacy Environment Predict Language and Early Literacy in Indonesian Low SES Kindergartners
Patricia Adam, Mienke Droop, Tijs Kleemans, Eliane Segers
Reading & Writing Quarterly.2025; 41(6): 461. CrossRef - Linking Nighttime Smartphone Location, Sleep Quality, and Depressive Symptoms in Bangladeshi Young Adults: The Mediating Role of Bedtime Smartphone Use
Md. Rohmotul Islam, Oli Ahmed, Md. Nurul Islam
Journal of Technology in Behavioral Science.2025;[Epub] CrossRef - Field dependent-independent cognitive style as a predictor of malevolent creativity: a multifaceted approach
Pierpaolo Zivi, Marco Giancola, Raffaella Nori, Laura Piccardi, Simonetta D'Amico, Massimiliano Palmiero
Frontiers in Psychology.2025;[Epub] CrossRef - Fast-paced and violent media exposure are positively associated with ADHD and impulsivity in college students
Nicole L. Hayes, Craig A. Anderson, Edward L. Swing
Frontiers in Psychology.2025;[Epub] CrossRef - What makes running club participants commit to exercise in an adaptive way? Perspectives from self-determination theory
Heejung Jung, Sungho Kwon, Taiwoo Kim
International Journal of Sport and Exercise Psychology.2025; : 1. CrossRef - The impact of social support and social constraints on sleep disturbances in patients with lung cancer undergoing chemotherapy: Serial mediators of sleep cognition and anxiety-depression
Zhige Yan, Lily Dongxia Xiao, Xiajun Guo, Ying Hu, Nina Wang, Yao Wang
Asia-Pacific Journal of Oncology Nursing.2025; 12: 100740. CrossRef - Fully memristive spiking neural network for energy-efficient graph learning
Tuo Shi, Lili Gao, Ruixi Zhou, Yang Tian, Pei Chen, Yanting Ding, Shuangzhu Tang, Huiqin Ma, Jian Lu, Hui Zhang, Zhanfeng Wang, Bo Lyu, Xumeng Zhang, Xiaobing Yan, Qi Liu
Science Advances.2025;[Epub] CrossRef - Can Environmental Docents Influence Visitors’ Environmentally Responsible Behavior? The Changes in Relationships Between Tourists’ Environmental Concern and Environmentally Responsible Behavior in a Coastal Protected Area
Yi Hsien Lin, Pi-Shen Ku, Huei-Tung Feng
Coastal Management.2025; 53(2): 179. CrossRef - Psychometric evaluation of the Bangla version of Body Image States Scale (B-BISS) for young adults in Bangladesh
Shakira Khatun, Nasim Rana Masud, Mohd. Ashik Shahrier
Journal of Science and Engineering Papers.2025; 02(02): 135. CrossRef - META—Measurement for Evolution, Transformation, and Autorealization: A New Assessment Protocol
Alessio Gori, Eleonora Topino
Behavioral Sciences.2025; 15(7): 942. CrossRef - Metabolomic profiling of a cholesterol lowering plant-based diet from two randomized controlled feeding trials
Andrea J. Glenn, Anne-Julie Tessier, Meaghan E. Kavanagh, Gloria A. Morgan, Clary B. Clish, Jordi Salas-Salvado, Vasanti S. Malik, Anthony J. Hanley, Richard P. Bazinet, Elena M. Comelli, Ahmed El-Sohemy, Simin Liu, Beatrice A. Boucher, Cyril W. C. Kendal
European Journal of Clinical Nutrition.2025; 79(9): 863. CrossRef - Examining Individual Earthquake Preparedness Behaviors in Istanbul, Türkiye: A Stage-Based Study Applying the Precaution Adoption Process Model
Ömer Demir, Nuran Aydemir
International Journal of Disaster Risk Science.2025; 16(3): 346. CrossRef - Trustworthiness Assessment of an Adaptive and Explainable Robot in a Real Environment
Filippo Cantucci, Marco Marini, Rino Falcone
International Journal of Social Robotics.2025; 17(10): 2199. CrossRef - Biochar effects on bacterial communities in recycled concrete aggregates
Jiaxin Liao, Yi Huang, Yijie Su, Haowen Guo, Junjun Ni, Denian Li, Haoran Yuan, Yong Chen
Frontiers of Environmental Science & Engineering.2025;[Epub] CrossRef - Linking spatiotemporal variations in urban land surface temperature to land use and land Cover: A case study in Hangzhou City, China
Yu Song, Huiyan Xu, Ting Liu, Junfeng Xu, Xiaodong Song
Ecological Indicators.2025; 173: 113336. CrossRef - Çevreye Özgü Hizmetkar Liderliğinin Çalışan Yeşil Davranışlarına Etkisi: Yeşil Rol Modelin Aracılık Rolü
Fatih Yavuzarslan, Nesrin Şalvarcı Türeli
Süleyman Demirel Üniversitesi Vizyoner Dergisi.2025; 16(46): 615. CrossRef - YETİŞKİNLERDE PSİKOLOJİK DAYANIKLILIK İLE BİLİNÇLİ FARKINDALIK, DUYGU DÜZENLEME VE SIKINTIYA DAYANMA ARASINDAKİ İLİŞKİLERİN İNCELENMESİ
Özlem Yılmaz Halıcı, Selma Arıkan
HUMANITAS - Uluslararası Sosyal Bilimler Dergisi.2025; 13(25): 430. CrossRef - Exploring the Influence of Mindful Observation, Biospheric Value and Personal Norms in Shaping Pro-environmental Behaviour Among Adolescents: A Mediation Analysis
Swedhaa Shanmathi V, Vinothkumar M
Journal of Human Values.2025;[Epub] CrossRef - Influence of Contact Lens Parameters on Tear Film Dynamics
Darshan Ramasubramanian, José Luis Hernández-Verdejo, José Manuel López-Alonso
Bulletin of Mathematical Biology.2025;[Epub] CrossRef - Comparing the effectiveness of mandala art and value clarification on the anxiety and emotional state of parents of children with cancer: A randomized controlled trial
Meltem Gürcan, Sevcan Atay Turan
European Journal of Oncology Nursing.2025; 75: 102835. CrossRef - Field study of biochar effects on vegetation and bacterial communities in a restored mine
Jia Xin Liao, Sanandam Bordoloi, Yu Chen Wang, Billy Chi Hang Hau, Charles W.W. Ng
Applied Soil Ecology.2025; 211: 106141. CrossRef - Unplugged gamification in education: Developing computational thinking skills through embodied gameplay
Athanasios Christopoulos, Stylianos Mystakidis, Chrysostomos Stylios, Ioannis G. Tsoulos
The Journal of Educational Research.2025; : 1. CrossRef - Échelle des théories implicites l’intelligence tournées vers soi (TIIS) : validation psychométrique en langue française auprès d’une population étudiante
M. Ahmida, L. Léger, F. Fenouillet
Psychologie Française.2025; 70(3): 209. CrossRef - Trajectories of Authentic Inner Compass in the College Years: Implications for Psychological Functioning among Chinese Students
Xiting Zhou, Cong Yi, Shun-Lam Chan, Jun Wei
Journal of Happiness Studies.2025;[Epub] CrossRef - Exploring the Relationship Between Financial Education, Financial Attitude, Financial Advice, and Financial Knowledge: Insights Through Financial Capabilities and Financial Well-Being
Arturo García-Santillán, Ma. Teresa Zamora-Lobato, Esmeralda Tejada-Peña, Liduvina Valencia-Márquez
Journal of Risk and Financial Management.2025; 18(3): 151. CrossRef - Exploring the role of shame and self-compassion on the link between fibromyalgia symptoms and depression: Insights from mediation and moderation analyses
Judite Fortuna, Ana M Pinto, José A. P. da Silva, Rinie Geenen, Paula Castilho
Journal of Health Psychology.2025;[Epub] CrossRef - Sensory processing sensitivity and health-related quality of life: the mediational role of coping strategies
Mercedes Borda-Mas, Magdalena Sánchez-Fernández, Nerea Almeda, Manuela Pérez-Chacón, Jose M. Mestre
Personality and Individual Differences.2025; 243: 113242. CrossRef - Performance in Multi-Joint Force-Plate Assessments in Male and Female CrossFit® Athletes
James R. Jowsey, G. Gregory Haff, Paul Comfort, Nicholas Joel Ripley
Biomechanics.2025; 5(2): 35. CrossRef - Validity and reliability of the Turkish version of the type 1 diabetes distress scale
Tuğba Bi̇lgehan, Elif Gençer Şendur, Özlem Canbolat, Emre Dünder, William H. Polonsky
Primary Care Diabetes.2025; 19(4): 383. CrossRef - Tendency to overeat predicts an elevated body mass index trajectory across school-age years
Catharina Sarkkola, Sohvi Lommi, Kris Elomaa, Eero Kajantie, Satu Männistö, Heli Viljakainen
Scientific Reports.2025;[Epub] CrossRef - Exploring individual's emotional and autonomous learning profiles in AI-enhanced data-driven language learning: An expanded sor perspective
Honggang Liu, Jiqun Fan, Miaoyue Xia
Learning and Individual Differences.2025; 122: 102753. CrossRef - The effect of laughter yoga on disease acceptance, treatment adherence and comfort in hemodialysis patients: A randomized controlled study
Betül BAL, Nagihan KÖROĞLU-KABA, Havva ÖZTÜRK, Yeter KURT, Aysel ÖZSABAN
EXPLORE.2025; 21(4): 103201. CrossRef - Nudity Norms and Breast Arousal: A Cross-Generational Study in Papua
Michal Mikolaj Stefanczyk, Piotr Sorokowski, S. Craig Roberts, Agnieszka Żelaźniewicz
Archives of Sexual Behavior.2025; 54(4): 1317. CrossRef - Statistical Tutorial for Cut‐Point Determination in Immunogenicity Studies
Yulia Mordashova, Xin Huang
Pharmaceutical Statistics.2025;[Epub] CrossRef - EQUANU: Equality in Societal and Professional Recognition of Nurses—A Cross‐Sectional Study on Societal and Professional Recognition of European Nurses
Elyne De Baetselier, Luis Manuel da Cunha Batalha, José Miguel Sousa Pedro Seguro, Nienke E. Dijkstra, Vigdis Abrahamsen Grøndahl, Jana Heczková, Ann Karin Helgesen, Rebeka Lekše, Manuel Lillo-Crespo, Alba Malara, Laura Petraglia, Andrea Pokorná, Mirko Pr
Journal of Nursing Management.2025;[Epub] CrossRef - Short-term effectiveness of gambling treatment in the Daily Clinic for Gambling Addiction
Dora Dodig Hundric, Neven Ricijas, Sabina Mandic, Sanja Radic Bursac, Davor Bodor
Frontiers in Psychology.2025;[Epub] CrossRef - Exploring the Influence of Online Price Anchoring and Attribute Framing on the Likelihood of Hearing Aid Purchases
Craig Richard St. Jean, Jacqueline Cummine, Gurjit Singh, William (Bill) Hodgetts
Audiology Research.2025; 15(2): 40. CrossRef - Analysis of Students’ Academic Performance in 2021 - 2023 Nigerian Senior School Certificate Examination Multiple Choice Objective Tests in Government
David Adebayo Adewuni, Michael Bamidele Ojo
International Journal of Education, Learning and Development.2025; 13(5): 1. CrossRef - Understanding parental support for children's 24‐hour movement behaviors based on an adapted HAPA framework: A three‐wave prospective study
Wei Liang, Guifang Liu, Ning Su, Ryan E. Rhodes, Yanping Duan, Chun‐Qing Zhang, Lingfei Wang, Lin Zhou, Hanxiao Zhu
Applied Psychology: Health and Well-Being.2025;[Epub] CrossRef - The “Japa-Japada” construct: A theoretical framework for exploring the recent medical brain drain scourge in Sub-saharan Africa and the potential medical reverse brain drain
Dara Thomas, Ying Li, Chiagoziem C. Ukwuoma, Joel Dossa
International Journal of Intercultural Relations.2025; 107: 102201. CrossRef - Unraveling willingness to communicate in Chinese as a second language
Yu Li
Australian Review of Applied Linguistics.2025;[Epub] CrossRef - Developmental Eye Movement (DEM) Test in Adults: Age-Related Changes and Italian Normative Data
Alessio Facchin, Silvio Maffioletti, Roberta Daini
Vision.2025; 9(1): 10. CrossRef - Predictive model of the relationship between social support, body image perception, and physical activity among university students
Xuejiao Gao, Xiaolin Wang, Chen Soon Chee, Shamsulariffin bin Samsudin, Muhammad Zarif Hassan, Luhong Ma, Pan Liu, Yuming Zhang
Humanities and Social Sciences Communications.2025;[Epub] CrossRef - The intersection of responsible leadership and entrepreneurial marketing: the roles of ethical climate, effective knowledge transfer and person-organization fit
Mohammad Hossein Khasmafkan-Nezam
Social Responsibility Journal.2025; 21(7): 1339. CrossRef - Enhancing patient-centered care with AI: a study of responses to neuroendocrine neoplasms queries
Francesco Panzuto, Alessandro Gallo, Marco Marini, Maria Rinzivillo, Manuela Albertelli, Chiara Maria Grana, Marco Maccauro, Massimo Milione, Salvatore Tafuto, Simona Barbi, Stefano Partelli, Maria Luisa Appetecchia, Giuseppe Badalamenti, Mirco Bartolomei
Endocrine.2025; 89(3): 921. CrossRef - Impulsivity Facets, Social Norms, and Co-Use of Alcohol and Cannabis
Melissa C. Rothstein, Amy L. Stamates
Journal of Drug Issues.2025;[Epub] CrossRef - Genomic approach to evaluate the intrinsic antibacterial activity of novel diazabicyclooctanes (zidebactam and nacubactam) against clinical Escherichia coli isolates from diverse clonal lineages in the United Arab Emirates
Farah Al-Marzooq, Akela Ghazawi, Maitha Alshamsi, Abdulrahman Alzaabi, Omar Aleissaee, Hamad Almansoori, Abdullah Alsaadi, Rauda Aldhaheri, Hafsa Ahli, Lana Daoud, Amna Ahmad, Timothy Collyns, Seema Oommen
Journal of Infection and Public Health.2025; 18(6): 102761. CrossRef - Psychometric Validation of the Gaming Disorder Scale for Adolescents (GADIS-A) in Dutch Among Flemish Adolescents
Eva Grosemans, Rozane De Cock, Lowie Bradt, Huub Boonen, Bart Soenens
Psychologica Belgica.2025; 65(1): 189. CrossRef - From Transformative Agency to AI Literacy: Profiling Slovenian Technical High School Students Through the Five Big Ideas Lens
Stanislav Avsec, Denis Rupnik
Systems.2025; 13(7): 562. CrossRef - Enhancing Subjective Well-Being in Young Professional Athletes: The Role of Self-Esteem and Perceived Social Support in Moderating Neuroticism
Serdar Solmaz
Sage Open.2025;[Epub] CrossRef - Bipolar spectrum risk and social network dimensions in emerging adults: Two social sides?
Stevi G. Ibonie, Gerald Young, Montana L. Ploe, Iris B. Mauss, Lauren B. Alloy, Jessica L. Borelli, Ben Bullock, Sarah R. Holley, Ellen Jopling, Shanmukh Kamble, Joelle LeMoult, Liam Mason, Daniel P. Moriarity, Robin Nusslock, Amie Okuma, Robb B. Rutledge
Journal of Social and Clinical Psychology.2025; 44(1): 1. CrossRef - Examining the relationship of competitive beliefs and social comparison orientations with engagement and performance of English language learners
Fatemeh Amini, Shakiba Es’haghi, Maryam Roghanizadeh, Nourollah Zarrinabadi
European Journal of Psychology of Education.2025;[Epub] CrossRef - THE MEDIATING ROLE OF COGNITIVE FLEXIBILITY İN THE RELATIONSHIP BETWEEN ALTRUISM AND MORAL VALUES OF CHILD DEVELOPMENT STUDENTS
Alper Eyinç, Esra Nur Tunç, Esin Sezgin
Selçuk Sağlık Dergisi.2025; 6(1): 97. CrossRef - Who is Hooked on AI? The Role of the Big Five Personality Traits in Compulsive ChatGPT Use Among Chinese Students
Yinyao Hu, Chee-Seng Tan, Shimeng Wang, Hanyun Zhang, Jiahui Qian, Yihan Wang
The Asia-Pacific Education Researcher.2025; 34(5): 1899. CrossRef - Çocukluk Çağı Travmaları ve Narsisistik Kişilik Özellikleri Arasındaki İlişkide Şema Modların Aracılık Rolü
Hüseyin Yolalan
AYNA Klinik Psikoloji Dergisi.2025; 12(2): 294. CrossRef - Unequal Access, Unequal Impact? The Role of Open Access Policies in Publishing and Citation Trends Across Three Countries
Shlomit Hadad, Daphne Raban, Noa Aharony
Publications.2025; 13(2): 20. CrossRef - Family Income and Parental Perceptions of Gifted Education: The Mediating Role of Parents’ Trust in Their Child’s Resilience
Ortal Slobodin, Yonit Manzur Prior, Tala Noufi, Halleli Pinson
Gifted Child Quarterly.2025;[Epub] CrossRef - Psychometric properties of the revised Ukrainian version of the Continuous Traumatic Stress Response scale (CTSR) in the context of the Russo-Ukrainian war
Iryna Frankova, Oksana Senyk, Oleksandr Avramchuk, Iryna Leshchuk, Andrii Rudys, Anton Kurapov, Aviva Goral
European Journal of Psychotraumatology.2025;[Epub] CrossRef - The Influence of Perceived Autonomy Support on Physical Activity Among High School Students: The Mediating Roles of Basic Psychological Needs
Zhou Wanwan, Ahmad Zamri Khairani
Behavioral Sciences.2025; 15(4): 536. CrossRef - Evlilikte Hayal Kırıklığı Ölçeğinin (EHÖ) Türkçe’ye Uyarlanması: Geçerlik Ve Güvenirlik Çalışması
Sabiha Yedirir, Şerife Işık, Sylvia Niehuis
Aile Psikolojik Danışmanlığı Dergisi.2025; 8(1): 1. CrossRef - Cultural translation of the constipation assessment a study on the reliability and validity of the Chinese version of the constipation severity index
Wei Hu, Madhulika G. Varma, Xiaoli Huang, Xin Wang, Ke Shang, Di Xu, Xia Li
Frontiers in Medicine.2025;[Epub] CrossRef - Effects of daily creative writing practice at school on the cognitive development of children from disadvantaged socio-economic backgrounds
Cédric Hubert, Nathalie Bonnardel, Aline Frey
Thinking Skills and Creativity.2025; 58: 101881. CrossRef - The association between problematic smartphone use and subjective well-being in Bangladeshi youths: Mediating role of sleep quality
Md. Rohmotul Islam, Oli Ahmed, Lutfun Naher, Md. Nurul Islam
Addictive Behaviors Reports.2025; 21: 100599. CrossRef - From Surface to Deep Learning: Gamified Mobile Education for Subcutaneous and Intramuscular Injection Skills
Zeynep Tamer, Esin Kavuran
Medical Science Educator.2025; 35(3): 1431. CrossRef - Choreographing Well-Being: The Predictive Role of Self-Compassion on Life Satisfaction—A Therapeutic-Based Art Pedagogy Perspective in Recreational Dance
Aglaia Zafeiroudi, Thomas Karagiorgos, Ioannis Tsartsapakis, Gerasimos V. Grivas, Charilaos Kouthouris, Dimitrios Goulimaris
Sports.2025; 13(7): 223. CrossRef - The longitudinal association between problematic Internet use and psychotic-like experiences in adolescents: Mediated by sleep disturbance and moderated by psychological resilience
Luowei Bu, Haoxian Ye, Dongfang Wang, Wenxu Liu, Dan Chen, Fang Fan
Addictive Behaviors.2025; 166: 108306. CrossRef - Digital Addiction, Perceived Helicopter Parental Attitudes and Dissociative Experiences: Examining Relationality in Adolescents
Sercan Mansuroğlu
Psychology in the Schools.2025; 62(8): 2731. CrossRef - The effect of variations in body shapes and sizes of Ethiopian young female consumers on the fit of ready-to-wear jeans
Berihun Bizuneh
International Journal of Fashion Design, Technology and Education.2025; : 1. CrossRef - Personality traits as predictors of vulnerability to persuasion in social engineering amongst risk-aware targets
Aya Muhanad, Israa Abuelezz, Raseena Haris, Khaled M. Khan, Raian Ali
Computing.2025;[Epub] CrossRef - Post-Traumatic Stress and Coping Strategies for Earthquake-Related Stress Among Individuals Affected by the February 6, 2023 Earthquakes: The Case of Malatya
Vehbi Bayhan, Ahmet Yasuntimur, Nesrin Demir
Fırat Üniversitesi Sosyal Bilimler Dergisi.2025; 35(2): 773. CrossRef - Biosimilars in practice: Discriminant factors influencing prescription decisions among physicians in Thailand
Chaoncin Sooksriwong, Ekapong Kachai, Wanruchada Katchamart, Ponlapat Rojnuckarin, Ekaphop Sirachainan, Tuangrat Phodha, Wenguo Cui
PLOS One.2025; 20(7): e0327591. CrossRef - TO SURVIVE OR TO DIE? CROSS-SECTORAL ANALYSIS OF MECHANISMS AND CHALLENGES OF SUCCESSION PLANNING BY AGRIPRENEURS IN GHANA
MAVIS SERWAH BENNEH MENSAH, KEREN NAA ABEKA ARTHUR, CHARLES HACKMAN KWAMENA ESSEL, ENOCH MENSAH-WILLIAMS, RICHARD ASUMADU, EDWARD NII AMAR AMARTEIFIO
Journal of Developmental Entrepreneurship.2025;[Epub] CrossRef - Association of the VNTR Polymorphism in the MIR137 Gene with Cognitive Functions in Schizophrenia Patients and Healthy Individuals
M. V. Alfimova, G. I. Korovaitseva, V. V. Plakunova, V. E. Golimbet
Russian Journal of Genetics.2025; 61(1): 124. CrossRef - Blurring boundaries: the draining impact of proactive personality on remote workers’ well-being
Silvia De Simone, Jessica Pileri, Marina Mondo, Maria Luisa Farnese, Max Rapp-Ricciardi, Barbara Barbieri
International Journal of Organizational Analysis.2025;[Epub] CrossRef - A Study on the Effect of Fear of Negative Evaluation on Restrained Eating and Its Intervention among Female College Students
Sisi Li, Weijian Fu, Wenyi Liu, Nailiang Zhong
International Journal of Mental Health Promotion.2025; 27(2): 137. CrossRef - Factors associated with nursing and midwifery students’ satisfaction with the clinical learning environment: a cross-sectional study in Morocco
Khadija Guejdad, Laila Lahlou, Ali Ikrou, Redouane Abouqal, Jihane Belayachi
BMC Nursing.2025;[Epub] CrossRef - Psychometric properties of full WHODAS 2.0 questionnaire for application through phone surveys: an experience in PERSIAN traffic cohort
Nasrin Shahedifar, Homayoun Sadeghi-Bazargani, Mina Golestani, Mohammad Asghari Jaafarabadi, Faramarz Pourasghar, Shahrzad Bazargan-Hejazi
Discover Public Health.2025;[Epub] CrossRef - Inflammation and minority stress: A moderated mediation model of childhood adversity and mental health in young men who have sex with men
Laura H. Dosanjh, Cynthia Franklin, Yessenia Castro, Bridget Goosby, Fiona N. Conway, Frances A. Champagne, Luis A. Parra, Jeremy T. Goldbach, Michele D. Kipke
Social Science & Medicine.2025; 376: 118119. CrossRef - Validity and reliability of the Turkish version of the Fear of Cancer Scale
Mehmet Halil Öztürk, Ahmet Doğan Kuday
Journal of Health Psychology.2025;[Epub] CrossRef - When Eating Healthy Becomes Unhealthy: A Cross-Cultural Comparison of the Indirect Effect of Perfectionism on Orthorexia Nervosa Through Obsessive–Compulsive Symptoms
Alexandra Cobzeanu, Ioana-Cătălina Roman, Iulia Cristina Roca
Psychiatry International.2025; 6(1): 16. CrossRef - Adaptation and Validation of the Scale for Chinese Preschool Teachers’ Self-Efficacy (SCPTSE): Based on Classical Test Theory and Item Response Theory
Hao Lu, Xiumin Li, Kejian Li
Behavioral Sciences.2025; 15(6): 741. CrossRef - Deep learning-based hybrid SEM-neural network approach for predicting mobile application adoption in whistleblowing services
Yelkal Mulualem Walle
International Journal of Disclosure and Governance.2025; 22(4): 896. CrossRef - Longitudinal Associations Between Academic and Social Adjustment Among Chinese College Freshmen: The Mediating Role of Depressive Symptoms
Yonghe Ti, Cong Yi, Jun Wei, Guangyuan Shi
Emerging Adulthood.2025; 13(3): 663. CrossRef - Effectiveness of nurses’ training about mechanical ventilation weaning on neonatal outcomes
Mohammed F. Alharbi, Salwa A. Marzouk, Nojoud Alrashidi, Mohammed H. Abu-Alghayth, Eman A. Mater, Marwa A. Ibrahim, Huwida Hamdy Abdelmonem, Hanan A. Mohammed, Shadia A. Syan, Aml S. Abdelrahem, Ahlam D. Alshehri, Shimaa M. Moursy, Abeer A. Almowafy, Fara
BMC Nursing.2025;[Epub] CrossRef - Severity, uncertainty, social support and coping style of parents who have children with epilepsy: a structural equation model
Miao Zhang, Liyun Lei, Dan Yao, Yongai Zhang
Frontiers in Neurology.2025;[Epub] CrossRef - Exploring emotional regulation, well-being, and academic engagement: A comparative study among Chinese high school and college EFL learners
Hong Shi, Wei Sun
Journal of Applied Developmental Psychology.2025; 98: 101773. CrossRef - EnsembleXAI-Motor: A Lightweight Framework for Fault Classification in Electric Vehicle Drive Motors Using Feature Selection, Ensemble Learning, and Explainable AI
Md. Ehsanul Haque, Mahe Zabin, Jia Uddin
Machines.2025; 13(4): 314. CrossRef - Effects of a group‐based compassion microintervention compared to cognitive reappraisal training on cardiovascular, self‐reported, and behavioral stress reactivity among young adults: A cluster randomized controlled trial
Emily C. Helminen, Kriti Behari, Jillian R. Scheer, Joshua C. Felver
Applied Psychology: Health and Well-Being.2025;[Epub] CrossRef - The impact of perceived teacher support on students’ learning approach: the chain mediating role of academic engagement and achievement goal orientation
Yaqi Zhang, Xiangli Guan, Jingjing Wang, Sumei Yin, Xuejiao Li, Yang Li, Mary C. Jobe, Md Zahir Ahmed
Frontiers in Psychology.2025;[Epub] CrossRef - The Ongoing Development of Mubsereen: An R Package for Students with Visual Impairment or Blindness
Jaime Fuentes-Balderrama, Qusay S. Hussein Al-Mamari, Catherine A. Harwood
Teaching of Psychology.2025;[Epub] CrossRef - The impact of emoticons on women’s friendships on Facebook
Amr Assad
Online Journal of Communication and Media Technologies.2025; 15(2): e202519. CrossRef - Impact of Probiotic Lacticaseibacillus paracasei Strain Shirota (LcS) on Aflatoxin Exposure among Healthy Malaysian Adults: A Randomized, Double-Blind, Placebo-Controlled Intervention Study
Wei Lin Chang, Takuya Akiyama, Jia-Sheng Wang, Heng Yaw Yong, Faezah Hassan, Hazizi Abu Saad, Rosita Jamaluddin, Mohd Redzwan Sabran
The Journal of Nutrition.2025; 155(7): 2110. CrossRef - Do Technologies Damage Our Personal Life? The Association of Technostress and Work-Life Fit for Employees’ Psychological Well-Being: A Cross-Cultural Mediation Model
Rossella Bottaro, Katya De Giovanni, Palmira Faraci
Psychological Reports.2025;[Epub] CrossRef - Smartphone addiction among elderly individuals: its relationship with physical activity, activities of daily living, and balance levels
Oguzhan Bahadir Demir, Aylin Bilgin, Feride Taskin Yilmaz
BMC Public Health.2025;[Epub] CrossRef - Neural basis of the association between future time perspective and ADHD characteristics: functional connectivity between Left inferior parietal lobule and mPFC
Mingzhen Ding, Rong Zhang, Tingyong Feng
Progress in Neuro-Psychopharmacology and Biological Psychiatry.2025; 140: 111427. CrossRef - The relationship between perceived usability and perceived credibility of Middle school teachers in using AI chatbots
Van-Da Can, Van-Hanh Nguyen
Cogent Education.2025;[Epub] CrossRef - From Public Value to Adoption: Understanding the Mediators of ICT Use in Smart Cities
Shuo Fei
VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations.2025; 36(4): 525. CrossRef - Muscle strength and fatigue asymmetry in university football players: Implications for training, injury prevention and rehabilitation
Bernelee Denize Doherty Spangenberg, Linda Van Den Berg, Suzanne Jacobs, Mzwandile Prescott Mahlangu
African Journal for Physical Activity and Health Sciences (AJPHES).2025; 31(2): 243. CrossRef - Gender moderates the mediating effect of psychological capital between physical activity and depressive symptoms among adolescents
Xiangyu Luo, Hanqi Liu, Zhaoyang Sun, Qin Wei, Jianhua Zhang, Tiancheng Zhang, Yang Liu
Scientific Reports.2025;[Epub] CrossRef - Factors Related to Depressive Symptoms in People with Gambling Disorder
Jong Min Choi, Eun Jin Lee
Issues in Mental Health Nursing.2025; 46(8): 775. CrossRef - The role of child language ability and parental mentalization in early child dysregulation
Sara Cibralic, Mary Xu, Nancy Wallace, Susan Morgan, Angelique Roth, Hannah Chau, Jane Kohlhoff
Infant Mental Health Journal: Infancy and Early Childhood.2025;[Epub] CrossRef - Factors influencing AI adoption by Chinese mathematics teachers in STEM education
Wen Du, Yiming Cao, Muwen Tang, Fang Wang, Guofeng Wang
Scientific Reports.2025;[Epub] CrossRef - Examining the Effect of Health Communication Problems on Healthcare System Distrust: A Cross-Sectional Study
Zübeyde Ağalday, Hülya Keskin
Ebelik ve Sağlık Bilimleri Dergisi.2025; 8(1): 41. CrossRef - An eye-tracking study of gaze guidance and visual integration effects on attention, learning and instructor social presence
Sonny Rosenthal, John Komar, Vanessa Simin Ho
Technology, Pedagogy and Education.2025; 34(5): 567. CrossRef - Psychometric Evaluation of the Italian Mukbang Addiction Scale
Paolo Soraci, Mark D. Griffiths, Nadia Bevan, Renato Pisanti, Rocco Servidio, Kagan Kircaburun
Journal of Technology in Behavioral Science.2025;[Epub] CrossRef - Development and Validation of the Classroom Mindful Attention Regulation Scale (CMARS) for Emerging Adults
Mohd. Ashik Shahrier, Lutfun Naher, Masuma Parvin, Md. Mokaddes Ali, Nahida Sarkar, Md. Luthfor Rahman, Mim Mariha Nisha Mridha
Mindfulness.2025; 16(4): 1015. CrossRef - How and When Deviant Peer Affiliation Influence Non-Suicidal Self-Injury? Testing a Longitudinal Moderated Serial Mediation Model among Chinese Early Adolescents
Chengfu Yu, Xiaoyan Liao, Xingcan Ni, Huahua Wang
Child Psychiatry & Human Development.2025;[Epub] CrossRef - Ters Yüz Sınıf Modeline Dayalı Etkinlik Temelli Öğretimin Türkçeyi Yabancı Dil Olarak Öğrenen Öğrencilerin Yazma Becerilerine Etkisi
Kübra Öncü Yiğit, Tuncay Türkben
Milli Eğitim Dergisi.2025; 54(246): 649. CrossRef - Testing the art as adaptation hypothesis through artistic practice and reproductive success in Papua woodcarvers
Piotr Sorokowski, Marta Kowal, Jerzy Luty, Wiktoria Jędryczka, S. Craig Roberts, Anjan Chatterjee, Stephen Davies
Scientific Reports.2025;[Epub] CrossRef - The relationship between grit and L2 willingness to communicate among Chinese undergraduate students: the contributions of foreign language enjoyment and anxiety
Gengchun Li
Humanities and Social Sciences Communications.2025;[Epub] CrossRef - Peatland fires in Peninsular Malaysia act as primary source of dioxins, dioxin-like polychlorinated biphenyl, and particulate matter
Ahmad Shalihin Mohd Samin, Nur Batrisyia Hadfina Azmi, Mohd Talib Latif, Yin-Hui Leong, Tengku Sifzizul Tengku Muhammad, Wen Sheng, Norhaniza Amil
Environmental Monitoring and Assessment.2025;[Epub] CrossRef - Grit as the predictor of flow and buoyancy among Duolingo multiple language learners: the mediating roles of perceived competence and competitiveness
Nasser Jabbari, Nourollah Zarrinabadi, Fatemeh Amini
Journal of Multilingual and Multicultural Development.2025; : 1. CrossRef - Associations between sleep health and familial social support, intragroup marginalization, and conflict among Hispanic adults
Miguel A. Garcia, Ashley M. Lindquist, Joshua I. Torres, Anna D. Drozdova, Theodore V. Cooper
Journal of Behavioral Medicine.2025; 48(3): 544. CrossRef - Impact of Nordic hamstring breaking point angle on football player performance
Murat Koç, Niyazi Sıdkı Adıgüzel, Barışcan Öztürk, Hakan Engin, Aydın Karaçam, Umut Canli, Bekir Erhan Orhan, Pablo Prieto-González, Peter Sagat, Jason Perez, Maria Isip, Peter Bartik
PeerJ.2025; 13: e19275. CrossRef - Understanding the relationships between parenting, attachment, schemas and psychosis: A serial mediation analysis
Nadia Akers, Christopher D. J. Taylor, Katherine Berry
British Journal of Clinical Psychology.2025; 64(4): 939. CrossRef - Analysis of the characteristics of university common spaces that affect university students’ psychological restoration
Hongyan Wen, Hanzheng Lin, Xiao Liu, Weihong Guo, Bao-Jie He
Scientific Reports.2025;[Epub] CrossRef - The Relationship Between a Sustainable Healthy Lifestyle and Depression, Stress, and Anxiety: A Structural Model on the Mediating Role of Physical Literacy
Mehmet Akarsu, İsmail İlbak, Zeliha Çavuşoğlu, Ratko Pavlović, Ana Maria Vulpe, Adina Camelia Șlicaru, Nicolae Lucian Voinea, Cristina Ioana Alexe
Healthcare.2025; 13(14): 1646. CrossRef - Depression, anxiety, and stress among mothers of children with thalassemia in Bangladesh: a cross-sectional study
Farhin Islam, Senjuti Seemanta, Sonia Rezina, Afsana Mehrab, Enayetur Raheem, Mohammad Sorowar Hossain
BMC Women's Health.2025;[Epub] CrossRef - How and when can the start-up repair venture capital firms’ trust with an informational strategy after task conflict: a moderated mediation model
Ping Han, Shuwei Hao, Bingqing Luo
Asian Business & Management.2025; 24(3): 428. CrossRef - Cross-Cultural Adaptation and Preliminary Validation of the Italian Version of the Feeding-Swallowing Impact Survey for both Members of Parental Dyads
Alessandra Baffi, Valeria Crispiatico, Edoardo Nicolò Aiello, Beatrice Curti, Giulia De Luca, Barbara Poletti, Mariagrazia Buratti, Lorenzo Montali
Dysphagia.2025; 40(5): 1191. CrossRef - The reliability and validity of the Swedish translation of the Vertigo Symptom Scale – short form in a cohort with acute vestibular syndrome
Solmaz Surano, Erik Faergemann, Gabriel Granåsen, Jonatan Salzer
Annals of Medicine.2025;[Epub] CrossRef - Nurses’ perception of talent management scale (NPTMS): development, validation and psychometric properties
Duygu Gül, Betül Sönmez
BMC Nursing.2025;[Epub] CrossRef - Deprem Sonrası Travma Belirtilerinin Hatay İli Özelinde İncelenmesi
Sema Urnek, Bestami Kara
Selçuk Üniversitesi Sosyal Bilimler Enstitüsü Dergisi.2025; (56): 35. CrossRef - Nerve Conduction Studies of Phrenic Nerve: Normative Data
José Castro, Mamede de Carvalho
Journal of Clinical Neurophysiology.2025;[Epub] CrossRef - Development and validation of the learning schedule adherence scale (LSAS) for university students
Shakira Khatun, Mim Mariha Nisha Mridha, Md. Minhaz Uddin, Abdul Muktadir, Anika Tarannum, Md. Romiz Uddin Rudro, Mohd. Ashik Shahrier
Discover Education.2025;[Epub] CrossRef - Investigating the impact of adoption of smart healthcare technologies on quality of patient care using two-staged SEM-ANN approach
S. A. Rajashekhar, Kamal Sharma, Manoj Kumar Trivedi, Miguel Villagómez Galindo, Kalpana Singh, Ana Beatriz Martínez Valencia
Discover Public Health.2025;[Epub] CrossRef - Comprehensive Assessment of Technological Challenges In Photovoltaic Waste Recovery In India Using Principal Component Analysis and Analytic Hierarchy Process Models
Dinesh Yadav, Sanjeev Kumar, Prabhu Paramasivam, Praveen Kumar Kanti, Rupesh Gupta, Mohamed Yusuf
Global Challenges.2025;[Epub] CrossRef - Unveiling the Impact of Grit and Learning Agility on Academic Burnout Among Nursing Students: A Cross-Sectional Study
Ibrahim Abdullatif Ibrahim, Atallah Alenezi, Heba Rabea Hagrass, Hoda Reda Abdou
SAGE Open Nursing.2025;[Epub] CrossRef - Cognitive neuroscience approach to explore the impact of wind turbine noise on various mental functions
Agnieszka Rosciszewska, Maciej Buszkiewicz, Gabriela Dobrzynska-Kobylec, Anna Klichowska, Tomasz Przybyla, Blanka B. Nagy, Andrzej Wicher, Michal Klichowski
Humanities and Social Sciences Communications.2025;[Epub] CrossRef - Family Dysfunction and Problematic Media Use Among Chinese Preschool Children: A Moderated Mediation Model
Wei Hong, Jia Wang, Ru-De Liu, Zong-Kui Zhou
Media Psychology.2025; : 1. CrossRef - Online Intervention for Muscle Tension Dysphonia
Viann N. Nguyen-Feng, Patricia A. Frazier, Yuchen Liu, Erin Feddema, Benjamin Wils, Elizabeth Nikcevich, Ali Stockness, Kelvin O. Lim, Amanda C. Hu, Lisa Butcher, Stephanie Misono
JAMA Otolaryngology–Head & Neck Surgery.2025; 151(4): 351. CrossRef - Examining Factors Affecting the Social Media Usage Behaviors of Young Athletes
İsmail İlbak, Mehmet Akarsu, Serkan Düz, Yunus Emre İlbak
GSI Journals Serie A: Advancements in Tourism Recreation and Sports Sciences.2025; 8(2): 533. CrossRef - Exploring English proficiency, listening strategies, and self-efficacy in a workplace English course: a moderated serial mediation approach
Mu-Hsuan Chou, Wei-Chi Pan
Language Awareness.2025; : 1. CrossRef - Perceptions of Financial AI Assistants and Intentions Toward AI-Assisted Financial Products
Thanh Hung Nguyen, Trong Quang Vu
International Journal of Asian Business and Information Management.2025; 16(1): 1. CrossRef - Pathways Linking Microaggression to Intimate Partner Violence Perpetration Among Palestinians in Israel: The Role of Threat, Psychological Distress, and Gender
Heba Faiek Zedan
Journal of Family Violence.2025;[Epub] CrossRef - A precise and high-throughput assay for stem structural characteristics deepens understanding of lodging resistance in sorghum
Jianguo Li, Liyan Zhao, Hongzeng Fan, Falin Zhao, Dandan He, Bo Li, Jibin Wang, Guosheng Xie, Zhen Hu, Chuchuan Fan, Lingqiang Wang
BMC Plant Biology.2025;[Epub] CrossRef - Peaceful acceptance and struggle with terminal cancer: The role of mindfulness, self-compassion, and body image distress
Francesco De Vincenzo, Rossella Mattea Quinto, Luca Iani, Sieva Durante, Chiara Scalpelli, Luigi Lombardo
Palliative and Supportive Care.2025;[Epub] CrossRef - Driving sustainable transportation: analyzing consumer behavior toward used electric vehicles
Zhang Yi, Noppawan Wisedsind, Jakkrit Thavorn
Sustainable Futures.2025; 10: 100978. CrossRef - Cross-linguistic sharing of phonological awareness in word spelling among early Chinese-English literacy learners: A three-wave cross-lagged panel analysis
Jiexin Lin, Jiayun Li
Learning and Individual Differences.2025; 120: 102691. CrossRef - Patient and staff perception of aggression and its management in a Lebanese psychiatric hospital: a cross-sectional study
Laura Abou Zeid, Chadia Haddad, Souheil Hallit, Georges Haddad
Discover Mental Health.2025;[Epub] CrossRef - Dış ticaret firmalarında çalışanların ekosentrik, antroposentrik ve çevreye yönelik antipatik tutumlarının değerlendirilmesi
Günseli Acar, Serap Özbaş
Kayseri Üniversitesi Sosyal Bilimler Dergisi.2025; 7(1): 24. CrossRef - Deepening our understanding concerning PhD candidates learning and risk of burnout while doing thesis work
Telle Hailikari, Henna Asikainen, Reijo Sund, Anna Parpala
Studies in Graduate and Postdoctoral Education.2025;[Epub] CrossRef - Assessing factor structure and measurement invariance of WISC-IV among almajiris attending quranic schools and pupils attending mainstream public primary schools in Northern Nigeria
Aishatu Abubakar-Abdullateef, Kwabena Kusi-Mensah, Luning Sun, Abdulaziz Mohammed, Taiwo L. Sheikh
Applied Neuropsychology: Child.2025; : 1. CrossRef - Clinicians' Assessment of Antisocial Personality Disorder (ASPD): A Network Analysis Approach on DSM‐5‐TR Criteria and Domains
Alessio Gori, Eleonora Topino, Carla Sharp
Personality and Mental Health.2025;[Epub] CrossRef - Motivations for Pet Ownership Among Adolescents and Emerging Adults in China: A Theory of Planned Behavior Study
Xiaoshan Yin, Paul Graham Morris, Joanne M. Williams
Anthrozoös.2025; : 1. CrossRef - Sociocultural Attitudes Toward Appearance and Attitudes Toward Eating in Adolescents With Type 1 Diabetes: The Importance of Perfectionism
Desireé Ruiz-Aranda, Ana Luque, Francesca Russo, Javier Fenollar-Cortés, Ben Wheeler
Pediatric Diabetes.2025;[Epub] CrossRef - Enhancing workplace support digitally: evaluating the impact of a job crafting and a wise intervention
Nora Böttcher, Simone Kauffeld
Gruppe. Interaktion. Organisation. Zeitschrift für Angewandte Organisationspsychologie (GIO).2025; 56(1): 17. CrossRef - Extracurricular physical activities and academic achievement in Saudi female physical education students: the mediating effect of motivation, enjoyment, and BMI
Mohamed Frikha
Frontiers in Psychology.2025;[Epub] CrossRef - Evaluating the impact of a nationwide educational policy on adolescent mental health in China: A longitudinal network analysis
Haoxian Ye, Yifan Zhang, Huolian Li, Xuan Wang, Yuyi Yao, Xinyu Shi, Yijia Liu, Dongfang Wang, Fang Fan
Applied Psychology: Health and Well-Being.2025;[Epub] CrossRef - The effect of learning strategies on offloading decisions in response recall
Jenna R. Donet, Philip H. Marshall, Michael J. Serra
Memory & Cognition.2025;[Epub] CrossRef - Factors associated with resilience among patients with end-stage kidney disease receiving hemodialysis in a teaching hospital: a cross-sectional study
Bimala Poudel, Rekha Timalsina
BMC Nephrology.2025;[Epub] CrossRef - Teacher conceptions of assessment and feedback predicting formative feedback practices: helping students to not ignore improvement-oriented feedback
Gavin T. L. Brown, Catarina Andersson, Mikael Winberg, Björn Palmberg, Torulf Palm
Scandinavian Journal of Educational Research.2025; : 1. CrossRef - Factors affecting students' sense of inclusion in the undergraduate engineering program at Waipapa Taumata Rau (The University of Auckland)
Priyanka Dhopade, James Tizard, Penelope Watson, Ashleigh Fox, Tom Allen, Hazim Namik, Aryan Karan, Rituparna Roy, Kelly Blincoe
Journal of Engineering Education.2025;[Epub] CrossRef - A Finer‐Grained Exploration of Morphological Knowledge in EFL Reading Among Chinese College Learners: Mediation Through Vocabulary and Grammar Knowledge
Zhenxia Pei, Haomin Zhang, Hanqiong Xu, Rongrong Sun, Xing Zhang
International Journal of Applied Linguistics.2025;[Epub] CrossRef - The Relationship Between Doomscrolling, Artificial Intelligence Anxiety, and Job Finding Anxiety Among University Students
Hayri Cengiz
OPUS Toplum Araştırmaları Dergisi.2025; 22(4): 627. CrossRef - Enhancing Chinese EFL University Students’ self-regulated learning through AI chatbot intervention: Insights from achievement goal theory
Juan Gu, Quanyong Liu
Learning and Motivation.2025; 92: 102191. CrossRef - Professionalism as a Moderator of the Effects of Authentic Leadership: Both Substitute and Enhancer
Liu Ziyu, Wong Hung
Nonprofit Management and Leadership.2025;[Epub] CrossRef - The Other as Shamer Scale: Validation of an Instrument to Assess External Shame
Sara Patricia Ríos Mercado, Antonio Tena Suck, María Emilia Lucio y Gómez Maqueo, Ana Lilia Villafuerte Montiel, Jaime Fuentes-Balderrama
Salud mental.2025; 48(3): 157. CrossRef - Nomophobia Levels in Turkish High School Students: Variations by Gender, Physical Activity, Grade Level and Smartphone Use
Piyami Çakto, İlyas Görgüt, Amayra Tannoubi, Michael Agyei, Medina Srem-Sai, John Elvis Hagan, Oğuzhan Yüksel, Orhan Demir
Youth.2025; 5(3): 78. CrossRef - Rethinking teaching skills: growth teaching mindsets predict teachers’ positive emotions and effective management in EFL classrooms
Nourollah Zarrinabadi, Nigel Mantou Lou, Mohsen Rezazadeh
Social Psychology of Education.2025;[Epub] CrossRef - Exploring Prospective Relationships of Emotion Regulation Difficulties With Eating Disorder Psychopathology and Eating‐Related Psychosocial Impairment Among Older Adults in China
Yueyang Xiao, Peiyi Wang, Wesley R. Barnhart, Chun Chen, Feng Ji, Jason M. Nagata, Jinbo He
European Eating Disorders Review.2025;[Epub] CrossRef - The moderating role of cognitive style on the relationship between critical thinking disposition, metacognitive awareness, and metacognitive strategies
Baiq Fatmawati, Hunaepi, Muhammad Asy'ari
Social Sciences & Humanities Open.2025; 12: 102006. CrossRef - Social media interference among college students: The role of social achievement goals and fear of missing out
Sungok Serena Shim, Boreum Kim, C. Addison Helsper, Mary Reas, Robyn Fisher, Mmesoma Asiegbu
British Journal of Educational Psychology.2025; 95(4): 1310. CrossRef - Artificial intelligence in academic libraries: a survey of users’ perception and adoption
Mohammad Haris, Anam Jamal Ansari, Basharat Ahmad Malik, Brady D. Lund, Naushad Ali
Global Knowledge, Memory and Communication.2025;[Epub] CrossRef - Depression, Anxiety, and Stress Scale-21 (DASS-21): Further psychometric exploration using robust item response theory and classical theory measures among university students
Md Dilshad Manzar, Mohammed Salahuddin, Dejene Nureye, Faizan Z. Kashoo, Majumi M. Noohu, Jazi Shaydied Alotaibi, Majed Sulaiman Alamri, Mark D. Griffiths, Mehdi Rezaei
PLOS One.2025; 20(7): e0325238. CrossRef - Examining the Interplay of Grit, Classroom Emotions, and Willingness to Communicate Among Chinese as a Second Language Learners: A Structural Equation Modeling Approach
Yu Li
Researching and Teaching Chinese as a Foreign Language.2025; 5(1): 71. CrossRef - Etik Liderlik Algısının Çalışan Motivasyonuna Etkisinde Çalışan Sadakatinin Aracı Rolü: Havacılık Sektörü Örneği
Rabia AKÇİN GÜRLER, Ahmet ERKASAP
Üçüncü Sektör Sosyal Ekonomi Dergisi.2025; 60(3): 2157. CrossRef - Development and Validation of the Robot Acceptance Questionnaire (RAQ)
Terry Amorese, Marialucia Cuciniello, Claudia Greco, Alfonsina D’Iorio, Edoardo Nicolò Aiello, Barbara Poletti, Vincenzo Silani, Nicola Ticozzi, Gabriella Santangelo, Gennaro Cordasco, Anna Esposito
Applied Sciences.2025; 15(17): 9281. CrossRef - The Protective Role of Savoring on Coping Motives for Cannabis Use and Consequences
Catherine D. Trinh, Rachel Girard, Alana Egan, Melissa R. Schick, Nichea S. Spillane
Journal of Psychoactive Drugs.2025; : 1. CrossRef - Mindfulness, emotion regulation, and mental health in Chinese college students: Cognitive reappraisal as mediator and neuroticism/openness as moderators
Jian Li, Linyan Man, Lijin Chen, Yiying Zhang, Zhaojie Wang
Acta Psychologica.2025; 260: 105552. CrossRef - Analysis of a Medically Certified, Wrist-Worn Sensor for the Assessment of Heart Rate and Energy Expenditure During Daily Activities in Patients With Chronic Heart Failure or Coronary Artery Disease and Recreational Athletes: Validation Study
Ignace L J De Lathauwer, Valerie A A van Es, Mayke M C J van Leunen, Steven Onkelinx, Rutger W M Brouwers, Danny A J P van de Sande, Mathias Funk, Hareld M C Kemps
JMIR Cardio.2025; 9: e69343. CrossRef - How does family face relate to intention to seek therapist-guided and digital self-guided psychological interventions? mediating effects of interdependent stigma and help-seeking attitudes
Ben C. L. Yu, Floria H. N. Chio, Rebecca Y. M. Cheung, Kriti Kakani, Winnie W. S. Mak
Social Psychiatry and Psychiatric Epidemiology.2025;[Epub] CrossRef - Unravelling consumer sentiments towards communicated health-safety and sustainability practices in hotels
Javier Perez-Aranda, Denis Tolkach, Euijoon Ahn, Fang-Wei Chen
Tourism and Hospitality Research.2025;[Epub] CrossRef - Hamilton Rating Scale for Anxiety: exploring validity with robust measures of classical theory parameters and a rating scale model in university students
Md Dilshad Manzar, Faizan Z. Kashoo, Mohammed Salahuddin, Dejene Nureye, Habtamu Acho Addo, Seithikurippu R. Pandi-Perumal, Amir H. Pakpour, Ahmed S. Bahammam
BJPsych Open.2025;[Epub] CrossRef - ‘‘Strengthening Connections’’: The Moderating Role of Leisure Satisfaction in the Relationship between Adjustment to University Life and Sense of Belonging
Cemal Yalçın, Mehmet Demirel
Research in Sport Education and Sciences.2025; 27(3): 217. CrossRef - Potential Interventions for Policy Support Targeting Justice-involved People with Mental Illness
Betel Hernandez, Jennifer Eno Louden
International Journal of Forensic Mental Health.2025; 24(4): 360. CrossRef - How do workplace ostracism and leader punishment behavior affect citizenship fatigue: the role of citizenship pressure and interpersonal sensitivity
Huiyue Liu, Hantai Zhang, Xuan Yu, Hui Xie
Current Psychology.2025; 44(20): 16385. CrossRef - Post-Traumatic Growth in Adults in Türkiye and Peru After Devastating Earthquakes at Different Times: A Cross-Cultural Study
Hacer Demirkol, Cristian Ramos-Vera, Elif Deniz Kaçmaz, Mehmet Yılmaz
OMEGA - Journal of Death and Dying.2025;[Epub] CrossRef - EXPERIMENTAL INVESTIGATION, MODELING, AND OPTIMIZATION OF POWER CONSUMPTION AND SURFACE ROUGHNESS IN 3D PRINTING OF PLA
ANANDITA NANDA, SUDHANSU RANJAN DAS, SMITA PADHAN, LALATENDU DASH, BISWARANJAN ROUT
Surface Review and Letters.2025;[Epub] CrossRef - Knowledge and perception of forensic science among junior police officers in Ghana
Jeffery Kweku Dadson, Elizabeth Wiafe, Solomon Asiedu, Benjamin Agyin, Afia Pinamang Owusu Ansah, Adriana Natekie Tetteyfio, Charlotte Agyemang
Journal of Forensic and Legal Medicine.2025; 115: 102949. CrossRef - Residential Colleges as Equalizers for Sustainable Development? Examining Impacts on Sustainable Education and Equity Across Gender and SES
Pingping Gui, Gazi Mahabubul Alam, Ciro Troise, Stefano Bresciani
Sustainable Development.2025;[Epub] CrossRef - Exploring Chinese Secondary EFL Students' Self‐Regulated Learning and Task Engagement in AI‐Assisted Classrooms: A Latent Growth Curve Modelling Study
Liu Shi, Shengji Li, Jingjing Xing
European Journal of Education.2025;[Epub] CrossRef - Are There Sex Differences in Wrist Velocity and Forearm Muscle Activity When Performing Identical Hand-Intensive Work Tasks?
Gunilla Dahlgren, Per Liv, Fredrik Öhberg, Lisbeth Slunga Järvholm, Mikael Forsman, Börje Rehn
Sensors.2025; 25(17): 5517. CrossRef - Agronomic Biofortification: Enhancing the Grain Nutritional Composition and Mineral Content of Winter Barley (Hordeum vulgare L.) Through Foliar Nutrient Application Under Different Soil Tillage Methods
Amare Assefa Bogale, Zoltan Kende, István Balla, Péter Mikó, Boglárka Bozóki, Attila Percze
Agriculture.2025; 15(15): 1668. CrossRef - The impact of loneliness on alexithymia among Chinese adolescents: the mediating role of problematic smartphone use and the moderating effect of fear of negative evaluation
Xiaowen Wu, Zihui Guo
BMC Public Health.2025;[Epub] CrossRef - Mediating roles of family functioning and self-efficacy in the relationship between depression and family resilience among kidney dialysis patients
Yuru Wang, Yanwei Yang, Qing Zeng, Fangqing Liu, Yiting Wang, Hongchen Zhang
BMC Psychology.2025;[Epub] CrossRef - Effects of 4-week velocity-based HIIT on athletic performance in youth soccer players
Murat Koç, Niyazi Sıdkı Adıgüzel, Hakan Engin, Barışcan Öztürk, Umut Canli, Aydın Karaçam, Bekir Erhan Orhan, Pablo Prieto-González, Peter Bartik, Shahad Alghemlas, Maria Isip, Peter Sagat
PeerJ.2025; 13: e20066. CrossRef - Harnessing information system capabilities to enhance organizational agility: the interplay of green absorptive capacity, collaborative knowledge creation, and strategic flexibility
Mohammad Hossein Khasmafkan-Nezam
Journal of Enterprise Information Management.2025; : 1. CrossRef - In the End: Associations Between Sleep Disturbance and Functional Impairment in Fibromyalgia—A Path Analysis Study
Kristoffer Bothelius, Eva Kosek, Markus Jansson‐Fröjmark
Journal of Sleep Research.2025;[Epub] CrossRef - Integrating intellectual capital and sustainable leadership to strengthen green business innovation and sustainability of SMEs
Naseer Ahmad, Waqas Khan, Ali Raza Elahi, Muhammad Haris
Journal of Enterprise Information Management.2025; : 1. CrossRef - Okul Öncesi Dönemde Psikolojik Sağlamlık ve Problem Davranışlar Arasındaki İlişkinin İncelenmesi
İrem Topuz, Olcan Aslan, Ahmet Bedel
Dokuz Eylül Üniversitesi Buca Eğitim Fakültesi Dergisi.2025; (65): 3345. CrossRef - Relationship between creativity and schizophrenia: a study of patients with psychiatric disorders
Angelica De Sandi, Giordano D’Urso, Edoardo Nicolò Aiello, Natale Vincenzo Maiorana, Mariachiara Calloni, Denise Mellace, Angelica Marfoli, Gaia Del Prete-Ferrucci, Barbara Poletti, Sergio Barbieri, Alberto Priori, Roberta Ferrucci
International Journal of Psychiatry in Clinical Practice.2025; 29(3): 160. CrossRef - Institutional environments, self-efficacy, outcome expectations and country context: serial mediating effects on entrepreneurial intentions and decision-making
Michael James J. Mustafa, Jia Wei Chin, Douglas Wegner, Melati Nungsari
Journal of Small Business and Enterprise Development.2025; 32(6): 1225. CrossRef - Synchronization of Cardiac and Musical Signals Improves Interoceptive, Cardiac, and Emotional Functioning
Ricardo Silva, Nélson Costa, Adriana Sampaio, Joana Coutinho
Applied Psychophysiology and Biofeedback.2025;[Epub] CrossRef - How grit enhances physical exercise in college students: mediating roles of personal growth initiative and self-efficacy
Chang Hu, Wen Zhang, Wenying Huang, Chanjuan Jin
Frontiers in Psychology.2025;[Epub] CrossRef - Okul Öncesi Öğretmenlerinin ve Öğretmen Adaylarının Yaratıcı Dramaya İlişkin Öz Yeterlik Algılarının İncelenmesi
Özlem Dönmez, Zeliha Irkiçatal, Aleyna Ecem Koç, Şebnem Aydın
Abant İzzet Baysal Üniversitesi Eğitim Fakültesi Dergisi.2025; 25(3): 2068. CrossRef - Lise Öğrencilerinin Okul Terki Risklerinin Çeşitli Değişkenlere Göre İncelenmesi
Melis Kavak, Tuncer Bülbül
Mersin Üniversitesi Eğitim Fakültesi Dergisi.2025; 21(2): 482. CrossRef - The role of health literacy in boosting citizen engagement in appropriate use of antibiotics
Marta Acampora, Greta Castellini, Walter Ricciardi, Leonardo Villani, Guendalina Graffigna
Journal of Public Health.2025;[Epub] CrossRef - Seeking Substitutive Satisfaction: The Influencing Mechanism of Loneliness on Tourists’ Pro-Environmental Behavior
Zhirui Qu, Chunxiao Li, Yufan Yang
Journal of Hospitality & Tourism Research.2025;[Epub] CrossRef - Chronic neck pain as an exacerbating factor for depressive symptoms in a 1-Year longitudinal population study
Seungwon Song, Jaewook Jeong, Jungyon Yum, Kyung Min Kim, Min Kyung Chu
Scientific Reports.2025;[Epub] CrossRef - Ground support equipment and flight delays: a multivariate analysis in different locations
Henrricco Nieves Pujol Tucci, Francesco Facchini
CEAS Aeronautical Journal.2025;[Epub] CrossRef - Psychometric properties of the German Stroke and Aphasia Quality of Life Scale 39 generic version
Caterina BREITENSTEIN, Katerina HILARI, Annette BAUMGAERTNER, Tanja GREWE, Agnes FLÖEL, Wolfram ZIEGLER, Peter MARTUS, Erich B. RINGELSTEIN, Walter HUBER, Karl G. HAEUSLER, Stefanie BRUEHL, Klaus WILLMES
European Journal of Physical and Rehabilitation Medicine.2025;[Epub] CrossRef - Effects of Generative AI Feedback and Interactive Video Assessment on Student Learning Achievement in Philological Content Creation Courses
Nikolaos Pellas
Journal of Educational Computing Research.2025;[Epub] CrossRef - Can ‘International Understanding’ be successfully taught in schools? – Empirical results from a regional university-school partnership project in Chengdu, China
Jun Teng, Chenhui Gao, Tingting Yuan, Xiaoli Jing, Yiyun Hu
International Journal of Educational Research.2025; 133: 102736. CrossRef - Longitudinal associations between problematic social media use and mental health: Mediating role of sleep
Oli Ahmed, Amy Dawel, Erin I. Walsh, Nicolas Cherbuin
Addictive Behaviors.2025; 170: 108446. CrossRef - The BODY-Q Belly Button Scale: A Development and Validation Study
Farima Dalaei, Claire E E de Vries, Charlene Rae, Trisia Breitkopf, Danny Mou, Maarten Hoogbergen, Jens Ahm Sørensen, Andrea L Pusic, Anne F Klassen
Aesthetic Surgery Journal.2025;[Epub] CrossRef - The effects of self-control exertion on subsequent physical performance in an alexithymic population
Hannah L. Graham, Ruth Boat, Simon B. Cooper, Noel P. Kinrade
Psychology of Sport and Exercise.2025; 81: 102962. CrossRef - Teacher professional development of digital pedagogy for inclusive education in post-pandemic era: Effects on teacher competence, self-efficacy, and work well-being
Yin Ru Shi, Kuen Fung Kenneth Sin, Yi Qing Wang
Teaching and Teacher Education.2025; 168: 105230. CrossRef - The effects of social comparison in social media on travel decision making: the role of fear of missing out
Donghee Kim, Patcharawan Wongsa
Journal of Hospitality and Tourism Technology.2025; 16(5): 1176. CrossRef - IMPACT OF PRODUCT PROMOTION VIDEOS ON CONSUMER BEHAVIOR: AN ANALYSIS THROUGH DIFFUSION OF INNOVATIONS THEORY ON YOUTUBE
İbrahim Halil Yaşar, Yusuf Zafer Can Uğurhan
İNİF E - Dergi.2025; 10(1): 294. CrossRef - Psychometric Properties of the Experience of Cognitive Intrusion of Pain (ECIP) Scale in Pediatric Chronic Pain
Cherish Heard, Keri R. Hainsworth, Kristen E. Jastrowski Mano
Children.2025; 12(8): 1069. CrossRef - Acrylic resin versus metal palatal base in complete dentures: A randomized crossover clinical trial of patient‐reported outcomes
Motasum Abu‐Awwad, Laila Hailkal, Mohammad Bustani, Nadia Ereifej, Dima Abu Baker, Mahmoud K. AL‐Omiri
Journal of Prosthodontics.2025; 34(8): 804. CrossRef - Facial Appearance and Markers of Cardiometabolic Risk in Healthy Adult Men
Wioletta Czernicka, Agnieszka Żelaźniewicz, Judyta Nowak-Kornicka, Bogusław Pawłowski
Archives of Sexual Behavior.2025; 54(7): 2491. CrossRef - Examining the Relationship between Perceived Environmental Identity and Pro-Environmental Behaviors among Students at Zanjan University of Medical Sciences
Elham Mohammadi, Khadijeh Hajimiri, Zohreh Farahmankia
Journal of Human Environment and Health Promotion.2025; 11(3): 168. CrossRef - Would we be anxious about the takeover request in conditionally automated driving? Understanding the impacts of situational factors and takeover performance on anxiety during role transitions
Binlin Yi, Jiarui He, Haotian Cao, Guibing Li, Wenfeng Guo, Xiaolin Song, Shaoka Su
Transportation Research Part F: Traffic Psychology and Behaviour.2025; 115: 103325. CrossRef - Dimensionality and Psychometric Properties of the Emotions‐Affect Systems ELicitation (EASEL‐3) in Fibromyalgia and the General Population: A Cross‐Cultural Study
Ana Margarida Pinto, Cristiana Campos Marques, Claúdia Figueiredo, Francisco J. Caramelo, Mariana Luís, Paula Castilho, Rinie Geenen, José A. P. da Silva
Clinical Psychology & Psychotherapy.2025;[Epub] CrossRef - Flexibly navigating cultural diversity: How polycultural identity facilitates a meaningful and rich life
Ariane Virgona, Matthew B. Ruby, Emiko S. Kashima
International Journal of Intercultural Relations.2025; 109: 102279. CrossRef - Percentile Distribution of Habitual-Correction Visual Acuity in a Sample of 1500 Children Aged 5 to 15 Years in Italy
Alessio Facchin, Marilena Mazzilli, Silvio Maffioletti
Pediatric Reports.2025; 17(4): 85. CrossRef - L2-Grit and Academic Buoyancy Among Tertiary-Level English Learners
Gökçe Dişlen Dağgöl
SAGE Open.2025;[Epub] CrossRef - The Role of Technophilia, Positive Experience and Flow in Enhancing Learning Efficiency in AI‐Based Music Education: A Self‐Determination Theory Approach
Pu Wang, Yijiang Liu
European Journal of Education.2025;[Epub] CrossRef - Factor structure and psychometric properties of the Hopkins Symptom Checklist: an evaluation with culturally and linguistically diverse adults in Australia
Nigar G. Khawaja, Min-Hsuan Tsai
Clinical Psychologist.2025; : 1. CrossRef - A loose hat on the organization’s head: cyberloafing among knowledge workers embedded in non-knowledge-intensive organizations
Ahmadreza Karimi Mazidi, Fariborz Rahimnia
Personnel Review.2025; 54(8): 2080. CrossRef - Anxiety and sleep hygiene among college students, a moderated mediating model
Jinyin Peng, Mengfen Liu, Ze Wang, Lei Xiang, Yang Liu
BMC Public Health.2025;[Epub] CrossRef - Exploring longitudinal associations of appetitive traits with thinness-oriented eating disorder symptomatology in Chinese older adults
Yueyang Xiao, Hana F. Zickgraf, Jinbo He
Eating Disorders.2025; : 1. CrossRef - Evaluation of the soil of Şırnak (Turkiye) by geotechnical SPT blow counts (SPT-N) with statistical approaches using electrical resistivity tomography (ERT) and shear wave velocity (Vs)
Gülen Tunç, Nuray Alpaslan
Acta Geophysica.2025;[Epub] CrossRef - Informatics competency, attitudes toward evidence-based practice, and clinical decision-making skills in nurses
Ahmad Salari, Seyyed Abolfazl Vagharseyyedin, Hakimeh Sabeghi
Health Informatics Journal.2025;[Epub] CrossRef - The boys’ club: gender biases in students’ evaluations of their philosophy professors
Pia Campeggiani, Marco Viola, Marco Marini
Philosophical Psychology.2025; : 1. CrossRef - The Mediating Role of Physical Literacy in the Relationship Between e-Health Literacy and a Sustainable Healthy Lifestyle Among Adolescents
Mehmet Akarsu, Mehmet Güllü, Gül Polat Günata, Aysel Kızılkaya, Savaş Aydın, Ecesu Özcan, Göktuğ Norman, Cihad Onur Kurhan
Healthcare.2025; 13(15): 1870. CrossRef - Intersecting identities, different struggles: The effects of demographics on experiences of discrimination and mental health outcomes among college students in Texas
Amanda Venta, Jesse Walker, Daniel O’Connell, Tessa Long, Cynthia M. Navarro Flores, Alejandro L. Vázquez, Gareth Hagger-Johnson,
PLOS Mental Health.2025; 2(9): e0000425. CrossRef - The Effects of Practice Environment and Job Characteristics on Nurses and Nurse Aides' Feelings of Powerlessness in Residential Long‐Term Care Institutions
Rong‐Fang Shih, Hsiang‐Chu Pai
Nursing & Health Sciences.2025;[Epub] CrossRef - The Effect of University Students’ Attitudes toward Artificial Intelligence on Academic Motivation and Procrastination Behavior
Gözde Önal
OPUS Toplum Araştırmaları Dergisi.2025; 22(4): 753. CrossRef - We Shift to Survive: Self-altering Strategies, Gendered Racial-Ethnic Socialization, and Well-being among Black College Women
Victoria A. McNeil-Young
Journal of Racial and Ethnic Health Disparities.2025;[Epub] CrossRef - Analyses of self-care agency and mindset: pilot study on Malaysian undergraduate medical students
Reshma Mohamed Ansari, Chan Choon Foong, Hidayah Mohd Fadzil, Mohamad Nabil Mohd Noor
The Asia Pacific Scholar.2025; 10(4): 35. CrossRef - Effects of Project Management Challenges on the Use of Sustainable Construction Materials: Evidence from Construction Industry Practitioners
Khalid Mehmood Sadar Din, Md. Sayuti Ishak
Civil and Environmental Engineering.2025;[Epub] CrossRef - Psychometric properties of the Turkish version of the eating pathology symptoms inventory (EPSI-T)
Fidan Turk, Pınar Acet, Goncagül Karabulut, Nazlı Akay
Cogent Psychology.2025;[Epub] CrossRef - Are autistic traits prospectively associated with various types of eating disorder psychopathology? A longitudinal study in Chinese adults
Junyu Yin, Yueyang Xiao, Phaedra Longhurst, Chuyi Tan, Yumeng Zhao, Zizhen Huang, Shuqi Cui, Jason M. Nagata, Jinbo He
Research in Autism.2025; 127: 202687. CrossRef - Parenting Responses as Transdiagnostic Treatment Targets in a Youth Partial Hospitalization Program
Katherine S. Benjamin, Sarah Taylor-Cavelier, Sarah M. Kennedy
Child Psychiatry & Human Development.2025;[Epub] CrossRef - Attention-deficit/hyperactivity disorder, sleep disturbances, and body mass index in college students
Alexa G. Deyo, Megan A. Milligan, Haley McBride, Kevin M. Antshel, Katherine M. Kidwell
Journal of American College Health.2025; : 1. CrossRef - Yükseköğretimde Öz ve Akran Değerlendirmelerinin Anlamlı Öğrenme Üzerine Etkisi
Müge Yurtsever Kılıçgün
Üniversite Araştırmaları Dergisi.2025; 8(3): 422. CrossRef - Fostering programming skill and critical thinking through AI-assisted PBL integration
Christian Basil Omeh, Musa Adekunle Ayanwale, Lindelani E. Mnguni, Chijioke Jonathan Olelewe
Journal of New Approaches in Educational Research.2025;[Epub] CrossRef - Workplace flexibility and subjective well-being: the role of work-life balance in Air Force women
Missiliana Riasnugrahani, Tery Setiawan, Andrew Batara
Cogent Business & Management.2025;[Epub] CrossRef - Overall fit of anterior and posterior single crown substructures fabricated with different additive manufacturing and conventional techniques
Gürel Pekkan, Hilal Gülgezen Aydın, Süleyman Hakan Tuna, Canan Hekimoğlu
Odontology.2025;[Epub] CrossRef - Decent work and economic growth in the South African agricultural sector
Petronella Jonck, Calvin Mabaso
South African Journal of Business Management.2025;[Epub] CrossRef - Changes in heartbeat-evoked potentials reflect changes in blood pressure
Arthur Plantard, Romain Séry, Vincent Pichot, Florian Chouchou
Journal of Neurophysiology.2025; 134(3): 830. CrossRef - Navigating the nexus of social appearance anxiety, learning autonomy, and collaborative dynamics in L2 acquisition: insights from Chinese university L2 learners
Weiqi Tian, Jing Liang, Yani Zhao, Mailihaba Aolan, Jingshen Ge
Frontiers in Psychology.2025;[Epub] CrossRef - The taste of trigeminal sensations: relation between taste, lingual tactile acuity, and spicy perception in patients with taste dysfunction
Mariano Mastinu, Max-Vincent Schönherr, Thomas Hummel
Chemical Senses.2025;[Epub] CrossRef - Reflective Realities: Exploring the Mechanisms of Mirror Dwelling in Social Virtual Reality
Aleksandra Zheleva, Annabel De Clercq, Emma Emmerechts, Durk Talsma, Klaas Bombeke
Media Psychology.2025; : 1. CrossRef - Exploring the Impact of HRM Practices on Organizational Effectiveness in the Indian Manufacturing Sector: a Comprehensive Analysis Using PLS-SEM and ANN
Manoj Vohra, Manoj Patwardhan, Yogesh Upadhyay
Public Organization Review.2025;[Epub] CrossRef - Investigating the effects of the Discovering Print through Play Program on print awareness skills of preschool children
Nilüfer Kurul, Neslihan Durmuşoğlu Saltalı
ODÜ Sosyal Bilimler Araştırmaları Dergisi (ODÜSOBİAD).2025; 15(3): 1556. CrossRef - Cognitive effects of adaptive deep brain stimulation in Parkinson’s disease: stability without risk
Roberta Ferrucci, Fabiana Ruggiero, Edoardo Nicolò Aiello, Sara Marceglia, Marco Prenassi, Barbara Poletti, Francesca Cortese, Tommaso Bocci, Denise Mellace, Mattia Arlotti, Natale Maiorana, Francesca Mameli, Linda Borellini, Filippo Cogiamanian, Enrico M
European Journal of Medical Research.2025;[Epub] CrossRef - The effect of foreign language enjoyment on the willingness to communicate of non-English majors: the mediating role of L2 grit and academic buoyancy
Chun Bai, Jiaying Hu
Frontiers in Education.2025;[Epub] CrossRef - The protective role of culture and family disapproval on substance use among American Indian adolescents
Rachel Girard, Catherine D. Trinh, Melissa R. Schick, Nichea S. Spillane
The American Journal of Drug and Alcohol Abuse.2025; : 1. CrossRef - Do shyness and emotions matter in shaping classroom engagement? A study of multilingual learners of Chinese in Thailand
Xian Zhao, Guangxiang Leon Liu, Liu Eerdemutu, Majid Elahi Shirvan
Journal of Multilingual and Multicultural Development.2025; : 1. CrossRef - Latent Variable Statistical Methods for Longitudinal Studies of Multi-Dimensional Health and Education Data: A Scoping Review
Meiyang Hong, Jane E. Harding, Gavin T. L. Brown
European Journal of Investigation in Health, Psychology and Education.2025; 15(9): 173. CrossRef - The Russian Version of Perceived Devaluation and Discrimination Scale
A. A. Zolotareva
Psychiatry (Moscow) (Psikhiatriya).2025; 23(3): 67. CrossRef - Maternal adverse childhood experiences and preschool children’s behavioral problems: exploring mediation via an adapted measure of adult attachment pattern
Stefan Kurbatfinski, Aliyah Dosani, Andrew F. Hayes, Deborah Dewey, Nicole Letourneau
Frontiers in Psychology.2025;[Epub] CrossRef - A STUDY ON THE EFFECT OF GREEN ACCOUNTING PERCEPTION ON GREEN ORGANIZATIONAL BEHAVIOR
Mustafa Atsan, Kürşad Çavuşoğlu
Journal of Academic Perspective on Social Studies.2025; (1): 110. CrossRef - The impact of Big Five personality traits on exercise motivation and mental health in college students: The mediating role of emotional intelligence
Yuan Zhang
Acta Psychologica.2025; 260: 105522. CrossRef - Development and Validation of the Japanese Version of the Triarchic Model of Grit Scale
Keigo Hatto, Daichi Sugawara, Hidehumi Hitokoto, Jesus Alfonso D. Datu
Journal of Psychoeducational Assessment.2025;[Epub] CrossRef - Social Comparison as a Moderator of the Relationships Between Romantic Partner Phubbing and Mental Health Among Hispanic Emerging Adults
Miguel A. Garcia, Angelica P. Aguirre, Marcos Lerma, Theodore V. Cooper
Cyberpsychology, Behavior, and Social Networking.2025;[Epub] CrossRef - Big Five personality traits, attitudes towards Artificial Intelligence and the use of AI solutions in foreign language learners
Czesław Kiński, Bartosz Kiński, Agata Przyborowska
Neofilolog.2025; (65/1): 65. CrossRef - The Mediating Role of Loneliness in the Relationship Between Insecurity Feelings and Internet Addiction
Biplob Kumar Dey, Kishor Roy
International Journal of Social Psychiatry.2025;[Epub] CrossRef - Semantic and phonemic advantages in Alzheimer's disease and behavioral variant-frontotemporal dementia: Insights from the Fluency Type Index
Edoardo Nicolò Aiello, Claudia Gendarini, Alessandro Cocuzza, Alessandra Romandini, Silvio Mauri, Beatrice Curti, Giulia De Luca, Federico Verde, Nicola Ticozzi, Matteo Mercurio, Emanuela Rotondo, Vittoria Borracci, Roberto Vimercati, Luca Sacchi, Tiziana
Journal of Alzheimer’s Disease.2025;[Epub] CrossRef - The German translation of the Oxford utilitarianism scale: Validation and the impact of the Covid-19 pandemic on the observations
Aistė Ambrasė, Malte Hendrickx, Melina Grahlow, Hong Yu Wong, Birgit Derntl, Ehsan Namaziandost
PLOS One.2025; 20(10): e0335215. CrossRef - Development and psychometric evaluation of the occupational adaptation scale for individuals with schizophrenia
Gülşah Zengin Yazıcı, Meral Huri
British Journal of Occupational Therapy.2025;[Epub] CrossRef - Contextual application of integrative neuromuscular training: motor skill competence in rural primary school children aged 8–10 years
Şeyma Öznur Gökşin, Özlem Kırandı, Burçak Keskin
Pedagogy of Physical Culture and Sports.2025; 29(5): 454. CrossRef - Effects of Sleep Extension on Musical Performance Skills
Benjamin Pelletier
Music & Science.2025;[Epub] CrossRef - Predictors of Desire to Avoid Pregnancy: The Roles of Marital Satisfaction and Fear of Childbirth
Semiha Unkazan, Nazli Unlu Bidik, Zekiye Turan, Döndü Sevimli Guler
BMC Women's Health.2025;[Epub] CrossRef - Androgen receptor gene polymorphism and biological age markers in men
Agnieszka Żelaźniewicz, Judyta Nowak-Kornicka, Adam Dąbrowski, Bogusław Pawłowski
Scientific Reports.2025;[Epub] CrossRef - Validating an instrument on gay fathers’ beliefs about socialising children conceived through surrogacy
Henny M. W. Bos, Mark Assink, Geva Shenkman, Salvatore D’Amore, Loes van Rijn-Van Gelderen, Nicola Carone
Journal of Reproductive and Infant Psychology.2025; : 1. CrossRef - Türk Savunma ve Havacılık Sanayisinde Üretim Faktörlerinin Analizi
Fethi Aslan
Verimlilik Dergisi.2025; 59(4): 985. CrossRef - Examining the mediating role of renewable energy awareness on the effect of social media marketing on patients’ evaluation of hospital services
Murat Başal, Turgay Karali̇nç, Festus Victor Bekun
Journal of Economic and Administrative Sciences.2025; : 1. CrossRef - A framework for investment scam reporting: Deception and reverse agency in an Australian context
Indra Abeysekera
Acta Psychologica.2025; 261: 105772. CrossRef - Protective factors against technostress in secondary school teachers
Pierpaolo Zivi, Gianluca Malatesta, Maria Lidia Mascia, Maria Grazia Diana, Alberto Di Domenico, Maria Pietronilla Penna, Massimiliano Palmiero
Scientific Reports.2025;[Epub] CrossRef - Exploring International Students’ Personal and Social Resources: Enhancing Academic Well-Being in the Medical Environment
Monica Adriana Vaida, Ramona Paloș, Adelina Maria Jianu, Nawwaf Sebastian Damen, Laura Octavia Grigoriță
Education Sciences.2025; 15(11): 1444. CrossRef - Growth L2 listening mindset, L2 listening self-efficacy, and L2 listening comprehension: the mediating role of L2 listening enjoyment
He Yang, Xinxin Wu
Innovation in Language Learning and Teaching.2025; : 1. CrossRef - Mental health literacy and anxiety in college students mediating role of psychological resilience and moderating role of physical exercise
Genghua Lei, Lingyu Li, Long Zhang
Scientific Reports.2025;[Epub] CrossRef - Improved olfactory function following high-frequency transcutaneous auricular vagal nerve stimulation in post-COVID-19 patients with olfactory dysfunction
Susanne Weise, Mária Oravcová, Pauline Hanslik, Coralie Mignot, Yusuf Ozgur Cakmak, Thomas Hummel
European Archives of Oto-Rhino-Laryngology.2025;[Epub] CrossRef - The Relationship between Maternal Reflective Functioning and Child’s Emotion Regulation and Social Skills and the Moderating Role of Paternal Reflective Functioning: A Descriptive Study
Golandam Mehraban, Samaneh Behzadpoor, Marzieh Ghoreyshi
Journal of Rafsanjan University of Medical Sciences.2025; 24(7): 581. CrossRef - WITHDRAWN: Construct Validity of the Dysfunctional Beliefs and Attitudes about Sleep Scale in Indonesian Adolescents
Anggi Setyowati, Henny Dwi Susanti, Min-Huey Chung
SSM - Mental Health.2025; : 100544. CrossRef - Triple perspective: assessing deep brain stimulation outcomes in Parkinson's disease
Denise Mellace, Francesca Mameli, Fabiana Ruggiero, Filippo Cogiamanian, Linda Borellini, Angelica De Sandi, Angelica Marfoli, Eleonora Zirone, Enrico Mailland, Elena Pirola, Antonella M. Ampollini, Luigi G. Remore, Marco Locatelli, Alberto Priori, Sergio
BMC Neurology.2025;[Epub] CrossRef - The early bird catches the worm, but falls exhausted from the branch at dusk: developing the FIPS – Facets of (Mal)adaptive precrastination scale
Christopher Gehrig, Philipp Yorck Herzberg
Current Psychology.2025;[Epub] CrossRef - Genetic link between granitic magmatism and hydrothermal vein-type quartz: Insights from the Lingqiushan deposit, Dabie Orogen, Central China
Weifeng Zhang, Liang Shan, Xin Deng, Jie Sun, Hui Liu, Liguo Zhang
Ore Geology Reviews.2025; 186: 106939. CrossRef - Knowledge, attitudes, and practices toward mpox among university health science students in Türkiye: a cross-sectional study
Ömer Ataç, Ayşe Nur Balcı Yapalak, Osman Hayran
BMC Medical Education.2025;[Epub] CrossRef - When learning with SLD is a hard challenge: a complex perspective on teacher-student relationships in primary school
Eleonora Florio, Alessia Cornaggia, Robert C. Pianta, Ilaria Castelli, Letizia Caso
Frontiers in Psychology.2025;[Epub] CrossRef - A network analysis of the relationship between perceived social support, emotion regulation, and job burnout among elementary and middle school teachers
Yueyao Li, Yuyang Nie, Zhaoming Ma, Cong Liu, Yuxian Cao, Guofeng Qu, Lijia Hou, Kangli Du, MingMing Guo, Tianci Wang, Xilai Zhu
Frontiers in Psychology.2025;[Epub] CrossRef - The Mediating Role of Mindful Eating in the Relationship Between Difficulties in Emotion Regulation and Emotional Eating
Aysu Bayram Saptır, Tuğba Seda Çolak Turan
İzmir Katip Çelebi Üniversitesi Sağlık Bilimleri Fakültesi Dergisi.2025; 10(3): 490. CrossRef - Cutoff value for Pediatric Weakness Scale for diagnosis of pediatric weakness
Tae-Hwan Kim, Han Chae, Ju-Hui Han, Mi-Ran Bang, Gyu-Tae Chang, Jin-Yong Lee, Sun-Haeng Lee
Journal of Integrative Medicine.2025;[Epub] CrossRef - Psychometric Properties of the Turkish Version of the Inpatient Experience With Nursing Care Scale (IPENCS)
Duygu Gül, Betül Sönmez, Merve Önal, Serap İleri
Nursing & Health Sciences.2025;[Epub] CrossRef - Developing Turkish-Sign-Language Self-Efficacy Scale for Learners based on various test theories
Pelin Piştav Akmeşe, Asiye Şengül Avşar, Nilay Kayhan, Necla Işıkdoğan Uğurlu, Zeynep Oral
International Journal of Assessment Tools in Education.2025; 12(4): 995. CrossRef - Okul Öncesi Öğretmen Adaylarının Mesleki Kaygı ve Mesleki Dayanıklılık İnançları Arasındaki İlişkinin İncelenmesi
Özlem Dönmez, Bahar Dağ
Türk Eğitim Bilimleri Dergisi.2025; 23(3): 2251. CrossRef - Differences in Personality Traits and Emotional Intelligence of Athletes and Non-Athletes: The Role of Gender and Performance Level
Duško Lepir, Ivana Pedović
Sportlogia.2025;[Epub] CrossRef - Measuring dementia knowledge and attitudes among the German Deaf community: Adaptation and validation of the Knowledge Assessment Scale, the Dementia Attitude Scale, and the Confidence in Dementia Scale in German Sign Language
Ioanna Antigoni Angelidou, Tarsitsa Ntova, Ege Karar, Marianna Tsatali, Birgit Teichmann
Journal of Alzheimer’s Disease.2025;[Epub] CrossRef - Exploring the Link Between Financial Health Indicators: Insights from Perception, Lived Experiences and Financial Resilience: A Study on Employees of a Sugar Mill Company
Esmeralda Tejada-Peña, Arturo García-Santillán, Belem Alejandra Contreras-Rodríguez
Journal of Risk and Financial Management.2025; 18(11): 606. CrossRef - The Levels of Emotional Awareness Scale (LEAS): Normative Data From a Community Sample and Observed Interactions With Sex, Marital Status, Education, and Age
Anne E. Chuning, Ning Li, Richard D. Lane, Ryan Smith
Psychological Reports.2025;[Epub] CrossRef - Measurement Equivalence and Behavioral Heterogeneity of Problematic Short Video Use: A Cross-Stage and Gender Comparative Study Among Adolescents Based on the Physiological-Psychological-Social Model
Zheng Mao, Yongzhi Jiang, Yisheng Yang
Psychological Reports.2025;[Epub] CrossRef - Actigraphic Sleep Health During Adolescence Predicts Young Adult Cardiovascular Health
Gina Marie Mathew, David A. Reichenberger, Lindsay Master, Orfeu M. Buxton, Anne-Marie Chang, Lisa Schneper, Norrina Bai Allen, Noreen Goldman, Donald M. Lloyd-Jones, Daniel A. Notterman, Lauren Hale
JACC: Advances.2025; 4(11): 102261. CrossRef - From unmet childhood needs to parenting attitudes: breaking the cycle
Lütfiye Kaya Cicerali
Advances in Mental Health.2025; : 1. CrossRef - The role of policy style in public participation: a case study of counterpart assistance policy in China
Yangcui Weng, Rajah Rasiah, Fumitaka Furuoka
Journal of Asian Public Policy.2025; : 1. CrossRef - Coffee and tea intake, circulating inflammatory biomarkers, and long-term risk of dementia: findings from two longitudinal studies
Minqing Yan, Jie Shen, Mengjia Zhao, Leqi Fei, Yuhui Huang, Minyu Wu, Ting Shen, Gulisiya Hailili, Dan Liu, Geng Zong, Yan Zheng, Dong Hang, Changzheng Yuan
European Journal of Epidemiology.2025;[Epub] CrossRef - Sex differences in chronotype distribution and their association with insomnia in a nationwide Korean survey
Jungyon Yum, Soomi Cho, Woo-Seok Ha, Seungwon Song, Jaewook Jeong, Kyung Min Kim, Wonwoo Lee, Min Kyung Chu
Chronobiology International.2025; : 1. CrossRef - The Swedish version of the BRIEF2: psychometric properties and age- and gender-related differences in executive functioning across multiple informants
Frida Ilahi, Eva Hoff, Daiva Daukantaitė
Child Neuropsychology.2025; : 1. CrossRef - Digital assessments boost science attitudes and sustainable education
Hannah Bosede Bankole, Musa Adekunle Ayanwale
Discover Sustainability.2025;[Epub] CrossRef - Telephone-based cognitive screening in neurodegenerative MCI and dementia: preliminary findings from the TBCS Study
Edoardo Nicolò Aiello, Beatrice Curti, Giulia De Luca, Arianna Moreschi, Valeria Crispiatico, Alessio Maranzano, Alina Menichelli, Tatiana Cattaruzza, Paolo Manganotti, Vincenzo Silani, Nicola Ticozzi, Federico Verde, Barbara Poletti
Neurological Sciences.2025;[Epub] CrossRef - Teaching identification as a protective and risk factor for teacher burnout in the context of role stress
Tyrone B. Pretorius, Anita Padmanabhanunni
Discover Psychology.2025;[Epub] CrossRef - Tele‐Genetic Versus Onsite Counseling for APOE Disclosure: A 6‐Month Study of Empowerment, Psychological Distress, and Behavioral Outcomes in Cognitively Diverse Individuals
Marina Makri, Ioanna Antigoni Angelidou, Despoina Moraitou, Liana Fidani, Thomas Tegos, Vasileios Kimiskidis, Magdalini Tsolaki
The Journal of Gene Medicine.2025;[Epub] CrossRef - Sociodemographic differences in young adult actigraphic sleep among a diverse, national sample: the Future of Families Young Adult Sleep Study
Gina Marie Mathew, David A Reichenberger, Carrie L Shandra, Lindsay Master, Adwoa Dadzie, Orfeu M Buxton, Anne-Marie Chang, Lauren Hale
Sleep Advances.2025;[Epub] CrossRef - The mediating role of physical activity attitude in the relationship between physical literacy and a sustainable healthy lifestyle in adolescents
İsmail İlbak, Mehmet Akarsu, Ladislav Cepicka, Petr Valach
Frontiers in Psychology.2025;[Epub] CrossRef - Nonlinear association between serum iron levels and moderate-to-severe uremic pruritus in peritoneal dialysis patients: a cross-sectional study
Wenjie Yu, Jing He, Zhiyao Bao, Zhaoting Li, Chunyan Zhang, Jingyuan Xie, Hong Ren, Xiaomin Huang, Tian Xu
BMC Nephrology.2025;[Epub] CrossRef - Sleep hygiene profiling, dysfunctional sleep beliefs, and their impacts on cancer-related fatigue in lung cancer patients undergoing chemotherapy
Zhige Yan, Xiajun Guo, Ying Hu, Li Liu, Yao Wang
Supportive Care in Cancer.2025;[Epub] CrossRef - The influence of parental expectations on adolescents’ physical activity: a chain mediation model of basic psychological needs and exercise motivation
Lumin Liu, Tianpei Li, Juan Long, Hwang Jin, Jae Woong Ahn
Frontiers in Psychology.2025;[Epub] CrossRef - University students' security behavior against email phishing attacks: insights from the health belief model
Anderson Kevin Gwenhure
Journal of Cybersecurity.2025;[Epub] CrossRef - Examining Correlates of Child Abuse with Adult Attachment and Sexual Satisfaction Among Adults
Areesha Azam, Cameron C. Brown, Dana A. Weiser, Kristy L. Soloski, Douglas B. Smith, Nicole Smalley, Kaitlyn Swecker, Ashley Gomes
Journal of Child Sexual Abuse.2025; : 1. CrossRef - A comprehensive guide to selecting the right modeling strategy for explanatory and predictive data analysis
Maysa Niazy, Heather M. Murphy, Khurram Nadeem, Nicole Ricker
Canadian Journal of Microbiology.2025; 71: 1. CrossRef - Multi-Field Functional Electrical Stimulation with Fesia Grasp for Hand Rehabilitation in Multiple Sclerosis: A Randomized, Controlled Trial
Olalla Saiz-Vázquez, Montserrat Santamaría-Vázquez, Aitor Martín-Odriozola, Tamara Martín-Pérez, Hilario Ortiz-Huerta
Technologies.2025; 13(10): 468. CrossRef - The Relationship Between Learning Motivation and English Achievement Among Undergraduate Non-English Majors in China: The Mediating Role of Self-Efficacy and Learning Strategies
Shuyan Liu, Haiying Sun
Sage Open.2025;[Epub] CrossRef - Psychometric Properties Of The Need For Cognitive Closure Scale In A Peruvian Sample: An ESEM Approach To Achieve An Acceptable Factor Solution And A Shorter Scale
Mauricio Enrique Silva-Alegria
Romanian Journal of Applied Psychology.2025; 27(1): 116. CrossRef - A semi-structured interview for the dimensional assessment of internalizing and externalizing symptoms in children and adolescents: Interview Version of the Symptoms and Functioning Severity Scale (SFSS-I)
Jana Rausch, Leonard Bickman, Nina Geldermann, Felix Oswald, Danny Gehlen, Anja Görtz-Dorten, Manfred Döpfner, Christopher Hautmann
Child and Adolescent Psychiatry and Mental Health.2024;[Epub] CrossRef - Bonding effectiveness of multi-step adhesive resin cements to CAD/CAM blocks: impact of thermal cycling and surface treatment methods
Seda Üstün Aladağ, Elif Aydoğan Ayaz
BMC Oral Health.2024;[Epub] CrossRef - Contributions of mothers' and fathers' shared book reading with infants at 9 months to language skills at 18 months in ethnically and socioeconomically diverse families
Yu Chen, Natasha Cabrera, Charlotte Sudduth, Stephanie M. Reich
Infant and Child Development.2024;[Epub] CrossRef - EMG coherence of foot and ankle muscles increases with a postural challenge in men
Chrysi Tsiouri, Ioannis G. Amiridis, Theodoros Kannas, Nikolaos Varvariotis, Chrysostomos Sahinis, Vassilia Hatzitaki, Roger M. Enoka
Gait & Posture.2024; 113: 238. CrossRef - Investigation into the Influence of Socio-Cultural Factors on Attitudes toward Artificial Intelligence
Seong-Won Kim, Youngjun Lee
Education and Information Technologies.2024; 29(8): 9907. CrossRef - Multidimensional analysis of supervisors’ safety leadership on safety violations of construction workers: An empirical investigation
Wenyao Liu, Qingfeng Meng, Zhen Li, Xijie Ai, Heap-Yih Chong
Work.2024; : 1. CrossRef - Learning to embrace one’s stress: the selective effects of short videos on youth’s stress mindsets
Audrey-Ann Journault, Rebecca Cernik, Sandrine Charbonneau, Claudia Sauvageau, Charles-Édouard Giguère, Jeremy P. Jamieson, Isabelle Plante, Steve Geoffrion, Sonia J. Lupien
Anxiety, Stress, & Coping.2024; 37(1): 29. CrossRef - Problematic Online Behaviours among University Students and Associations with Psychological Distress Symptoms and Emotional Role Limitations: A Network Analysis Approach
Magdalena Sánchez-Fernández, Mercedes Borda-Mas, Francisco Rivera, Mark D. Griffiths
International Journal of Mental Health and Addiction.2024;[Epub] CrossRef - Work social support on hospitality employees’ career optimism and turnover intention
Tam Bui Thi, Quyen Le Mai
Tourism Review.2024; 79(1): 119. CrossRef - The Impact of Relationship Quality on Couples With an Incarcerated Partner With Co-Occurring Mental Health and Substance Use Issues
Eman Tadros, Anh-Khoi Nguyen Le, Alexis Gregorash
Substance Use: Research and Treatment.2024;[Epub] CrossRef - L2 grit and language mindsets as predictors of EFL learners’ attitudes toward effectiveness and value of CALL
Nourollah Zarrinabadi, Mohsen Rezazadeh, Alireza Mohammadzadeh Mohammadabadi
Computer Assisted Language Learning.2024; 37(7): 1726. CrossRef - Understanding self-protective behaviors during COVID-19 Pandemic: Integrating the theory of planned behavior and O-S–O-R model
Yu Guo, Hongzhe Xiang, Yuhan Wang
Current Psychology.2024; 43(13): 12071. CrossRef - A report card assessment of the prevalence of healthy eating among preschool-aged children: a cross-cultural study across Australia, Hong Kong, Singapore, and the US
Alison Wing Lam Wan, Kevin Kien Hoa Chung, Jian-Bin Li, Shebe Siwei Xu, Derwin King Chung Chan
Frontiers in Nutrition.2024;[Epub] CrossRef - Measuring Psychological Strains: A Psychometric Study to Develop a Shortened Version of the Psychological Strain Scales
Ching Sin Siau, Jie Zhang, Won Sun Chen, Nur Zakiah Mohd Saat, Bob Lew, Xiaodong Ma, Kairi Kõlves
Behavioral Sciences.2024; 14(12): 1157. CrossRef - A Training Program Using Modified Joystick-Operated Ride-on Toys to Complement Conventional Upper Extremity Rehabilitation in Children with Cerebral Palsy: Results from a Pilot Study
Sudha Srinivasan, Patrick Kumavor, Kristin Morgan
Bioengineering.2024; 11(4): 304. CrossRef - The Relationship Between Cyberchondria and Health Anxiety in Pregnant Women
Duygu Gulec Satir, Sumeyye Bakir
Journal of Consumer Health on the Internet.2024; 28(2): 91. CrossRef - Adverse and Benevolent Childhood Experiences in University Students and Their Affective Forecasting and Event Predictions During the COVID-19 Pandemic
Grayden R. Wolfe, Angela J. Narayan, Kathryn R. Fox, Jenalee R. Doom
Adversity and Resilience Science.2024; 5(2): 159. CrossRef - The Complexity of Reading Revealed by a Study with Healthy Older Adults
Sara Pegoraro, Alessio Facchin, Francesca Luchesa, Elena Rolandi, Antonio Guaita, Lisa S. Arduino, Roberta Daini
Brain Sciences.2024; 14(3): 230. CrossRef - Behavioral Alterations of Spatial Cognition and Role of the Apolipoprotein E-ε4 in Patients with MCI Due to Alzheimer’s Disease: Results from the BDSC-MCI Project
Davide Maria Cammisuli, Virginia Bellocchio, Alessandra Milesi, Edoardo Nicolò Aiello, Barbara Poletti, Federico Verde, Vincenzo Silani, Nicola Ticozzi, Gloria Marchesi, Valentina Granese, Benedetta Vignati, Valeria Isella, Stefano Zago, Teresa Difonzo, S
Journal of Clinical Medicine.2024; 13(18): 5447. CrossRef - Anxiety, inhibitory control, physical activity, and internet addiction in Chinese adolescents: a moderated mediation model
Yang Liu, Yuan Jin, Jiawei Chen, Lianghao Zhu, Yongxiang Xiao, Lei Xu, Tiancheng Zhang
BMC Pediatrics.2024;[Epub] CrossRef - Vascular Cytokines and Atherosclerosis: Differential Serum Levels of TRAIL, IL-18, and OPG in Obstructive Coronary Artery Disease
Katharine A. Bate, Elijah Genetzakis, Joshua Vescovi, Michael P. Gray, David S. Celermajer, Helen M. McGuire, Stuart M. Grieve, Stephen T. Vernon, Siân P. Cartland, Jean Y. Yang, Mary M. Kavurma, Gemma A. Figtree
Biomolecules.2024; 14(9): 1119. CrossRef - Differences Between Clients and Professionals of Forensic and Nonforensic Flexible Assertive Community Treatment
Maartje Clercx, Genevieve van Tuijn
Journal of Forensic Nursing.2024; 20(2): E21. CrossRef - Similarities and differences in the psychological factors associated with generalised problematic internet use, problematic social media use, and problematic online gaming
Magdalena Sánchez-Fernández, Mercedes Borda-Mas, Zsolt Horvath, Zsolt Demetrovics
Comprehensive Psychiatry.2024; 134: 152512. CrossRef - Language development in Slovenian toddlers: the role of electronic media, parental knowledge of language development, and parental input
Urška Fekonja, Ljubica Marjanovič-Umek, Nika Pogorelc-Jesih, Naja Ferjan Ramírez
Frontiers in Developmental Psychology.2024;[Epub] CrossRef - Social Media Use, Emotional Investment, Self-Control Failure, and Addiction in Relation to Mental and Sleep Health in Hispanic University Emerging Adults
Miguel A. Garcia, Theodore V. Cooper
Psychiatric Quarterly.2024; 95(4): 497. CrossRef - The Mediating Role of Posttraumatic Stress Symptoms in the Relationship between Adult Attachment and Quality of Life
Gianluca Santoro, Vittorio Lenzo, Alessandro Musetti, Cristiana Caneglias, Lina Rita Crimi, Lucia Sideli, Adriano Schimmenti
European Journal of Investigation in Health, Psychology and Education.2024; 14(10): 2735. CrossRef - The rise of online group purchases in the age of pandemics
Chih-Chin Liang, Ying-Ting Gao
Technology in Society.2024; 77: 102598. CrossRef - Effects of Applying Problem Based Learning (PBL) Strategy Use on Students’ Oral Vocabulary as One Aspect of Speaking Performance
Fekadu Adam Jeldu, Zeleke Teshome Lucha, Jira Jabessa Feyisa
English Language, Literature & Culture.2024; 9(1): 16. CrossRef - Evaluation of an Integrated Fluency and Acceptance and Commitment Therapy Intervention for Adolescents and Adults Who Stutter
Alice K. Hart, Lauren J. Breen, Neville W. Hennessey, Janet M. Beilby
Journal of Speech, Language, and Hearing Research.2024; 67(4): 1003. CrossRef - Psychometric validation of the FACE‐Q Aesthetics Satisfaction with Temples scale in individuals seeking minimally invasive treatment to improve temple hollowing
Manraj N. Kaur, Vaishali D. Patel, Kelly X. Leung, Anne F. Klassen
Journal of Cosmetic Dermatology.2024; 23(11): 3517. CrossRef - The Impact of Compassion Writing Interventions on Body Dissatisfaction, Self-Compassion, and Fat Phobia
Kimaya R. Gracias, Lauren A. Stutts
Mindfulness.2024; 15(7): 1793. CrossRef - The frequency of using wearable activity trackers is associated with minutes of moderate to vigorous physical activity among cancer survivors: Analysis of HINTS data
Steven A. De La Torre, Trevor Pickering, Donna Spruijt-Metz, Albert J. Farias
Cancer Epidemiology.2024; 88: 102491. CrossRef - Prevention regulatory focus, desired cultural tightness, civic moral disengagement, and emotional reactions to normative daily transgressions: a serial mediation model among adults in Italy
Conrad Baldner, Antonio Pierro
Frontiers in Psychology.2024;[Epub] CrossRef - Psychosocial and personality trait associates of phubbing and being phubbed in hispanic emerging adult college students
Miguel A. Garcia, Marcos Lerma, Mariany Gainza Perez, Kevin Sandoval Medina, Andrea Rodriguez-Crespo, Theodore V. Cooper
Current Psychology.2024; 43(6): 5601. CrossRef - Family Economic Hardship and Non-Suicidal Self-Injury Among Chinese Adolescents: Relative Deprivation as a Mediator and Self-Esteem as a Moderator
Xiaoyan Liao, Huahua Wang, Xingcan Ni, Chengfu Yu
Behavioral Sciences.2024; 14(12): 1234. CrossRef - Hepatitis B Virus DNA-Level Change is Associated With Tumor Recurrence in Patients With Resected Hepatitis B Virus Hepatocellular Carcinoma
Won Tae Cho, Tae Yoo, Jung Min Lee, Jung Woo Lee, Hanbaro Kim, Ji Soo Lee, Sang Hyup Han
Journal of Surgical Research.2024; 295: 231. CrossRef - Impact of contextual factors on organisational performance mediated by talent management
Gladys B. Zake, Petronella Jonck, Anna-Marie Pelser
SA Journal of Industrial Psychology.2024;[Epub] CrossRef - Accurate Identification and Prosocial Behaviors Towards Human Trafficking Victims Among Psychology Students
Jeeva Babu, Grace M Boland, Temilola Salami
Journal of Human Trafficking.2024; 10(3): 430. CrossRef - Model predictive control of distributed energy resources in residential buildings considering forecast uncertainties
Felix Langner, Weimin Wang, Moritz Frahm, Veit Hagenmeyer
Energy and Buildings.2024; 303: 113753. CrossRef - Effects of cyber-security and trust issues on consumers’ intention to use E-commerce systems in rural South Africa
Vusani Netshirando , Armstrong Kadyamatimba, Willard Munyoka
International Journal of Research in Business and Social Science (2147- 4478).2024; 13(7): 538. CrossRef - Structure, network analysis, psychometric properties and clinical utility of the self-absorption scale in China
Xingwan Huang, Yixing Liu
BMC Psychiatry.2024;[Epub] CrossRef - A First Exploration: Can Eye Movement Desensitization and Reprocessing Improve Cognition in Older Adults With Posttraumatic Stress Disorder?
Ellen M. J. Gielkens, Gina Rossi, Sebastiaan P. J. van Alphen, Sjacko Sobczak
Journal of Geriatric Psychiatry and Neurology.2024; 37(3): 206. CrossRef - Impact of the restraint decision tree for physical restraint use in South Korean neurointensive care units
Jaejin Kang, Sol Kim, Minji Lee, Hyunjoo Na
Nursing in Critical Care.2024; 29(5): 1110. CrossRef - Marital adjustment and marital self-efficacy levels of married individuals based on former university accommodation
Begüm Özgün Erdoğdu Aslan, Alper Çuhadaroğlu
Türk Psikolojik Danışma ve Rehberlik Dergisi.2024; 14(74): 310. CrossRef - Undergraduate students’ opinions of peer-to-peer lending and pawnbroking: a comparison study in Vietnam
Thanh Hung Nguyen, Bình Nghiêm-Phú, Quang Trong Vu
Cogent Education.2024;[Epub] CrossRef - A quantitative case study of secondary school students’ level of statistical thinking
Salbiah Mohamad Hasim, Roslinda Rosli, Lilia Halim
Eurasia Journal of Mathematics, Science and Technology Education.2024; 20(4): em2421. CrossRef - Fast and Fun: A Pilot Feasibility Study Using Dual Joystick-Operated Ride-on Toys for Upper Extremity Rehabilitation in Children with Hemiplegia
Vaishnavi Shahane, Patrick D. Kumavor, Kristin Morgan, Sudha Srinivasan
Physical & Occupational Therapy In Pediatrics.2024; 44(6): 844. CrossRef - A randomized controlled trial on the effects of traditional Thai mind-body exercise (Ruesi Dadton) on biomarkers in mild cognitive impairment
Phaksachiphon KHANTHONG, Kusuma SRIYAKUL, Ananya DECHAKHAMPHU, Aungkana KRAJARNG, Chuntida KAMALASHIRAN, Vadhana JAYATHAVAJ, Parunkul TUNGSUKRUTHAI
European Journal of Physical and Rehabilitation Medicine.2024;[Epub] CrossRef - Regional brain activity and neural network changes in cognitive-motor dual-task interference: A functional near-infrared spectroscopy study
Hiroshi Miura, Yumie Ono, Tatsuya Suzuki, Yuji Ogihara, Yuna Imai, Akihiro Watanabe, Yukina Tokikuni, Satoshi Sakuraba, Daisuke Sawamura
NeuroImage.2024; 297: 120714. CrossRef - Psychological resilience, gaslighting and life satisfaction in a sample of Turkish women
Sezen Güleç, Ahmet Özbay
Women's Studies International Forum.2024; 105: 102945. CrossRef - Spatial distribution, source apportionment, and health risks assessment of trace elements in pre- and post-monsoon soils in the coal-mining region of North Karanpura basin, India
Prasenjeet Chakraborty, Siddharth Singh, Bodhisatwa Hazra, Alik S. Majumdar, Jyoti Kumari
Science of The Total Environment.2024; 955: 177173. CrossRef - Possibilities of Improving the Emission Characteristics of Passenger Cars by Controlling the Concentration Levels of Combustion-Generated BTEX Components
Dragan Adamović, Savka Adamović, Zoran Čepić, Slobodan Morača, Aleksandra Mihailović, Ivan Mijailović, Milena Stošić
Sustainability.2024; 16(24): 11033. CrossRef - ADHD and Risk of Precocious Puberty: Considering the Impact of MPH
Yi-Chun Liu, Yin-To Liao, Vincent Chin-Hung Chen, Yi-Lung Chen
Biomedicines.2024; 12(10): 2304. CrossRef - Personal Growth Initiative: Relation to Coping Styles, Strategies, and Self-Efficacy
Ingrid K. Weigold, Arne Weigold, Stephanie A. Dykema, Naomi M. Drakeford, Emily T. Ethridge
Journal of Happiness Studies.2024;[Epub] CrossRef - Kaygı Duyarlılığı ve Sağlık Kaygısı Arasındaki İlişkide Öz-Şefkatin Aracı Rolü
Selen Tütüncü, Esra Gül Koçyiğit
Akdeniz İnsani Bilimler Dergisi.2024; 14: 119. CrossRef - Exploring the Role of Distress Tolerance and Neuroticism in Internet Gaming Disorder Among USA Young Adult Daily Gamers
Mason L. Hatwan, Elizabeth Boyd, Surabhi Swaminath, Mahsa Mojallal
International Journal of Mental Health and Addiction.2024;[Epub] CrossRef - Key Drivers in the Adoption of the Demand Response Assessment System for Efficient Energy Management
Lanchaya Chitchaitheekul, Jakkrit Thavorn, Chupun Gowanit, Veera Muangsin
IEEE Access.2024; 12: 162217. CrossRef - Determinants of Parental Intention to Vaccinate Young Adolescent Girls against the Human Papillomavirus in Taiwan: An Online Survey Study
Pei-Yun Lin, Tai-Ling Liu, Li-Ming Chen, Meng-Jung Liu, Yu-Ping Chang, Ching-Shu Tsai, Cheng-Fang Yen
Vaccines.2024; 12(5): 529. CrossRef - Knowledge maps as a complementary tool to learn and teach surgical anatomy in virtual reality: A case study in dental implantology
Inês M. Lúcio, Bernardo G. de Faria, Renata G. Raidou, Luís Proença, Carlos Zagalo, José João Mendes, Pedro Rodrigues, Daniel Simões Lopes
Healthcare Technology Letters.2024; 11(6): 289. CrossRef - The relationship between self-control and internet gaming disorder and problematic social networking site use: the mediation effects of internet use motives
Ruoyu Zhou, Nobuaki Morita, Chunmu Zhu, Yasukazu Ogai, Tamaki Saito, Wenjie Yang, Mitsue Ogawa, Hong Zhang
Frontiers in Psychiatry.2024;[Epub] CrossRef - Affiliate Stigma and Parental Stress Among Parents of Children With Autism Spectrum Disorder: The Mediating Role of Shame
Daiana Maria Rusu, Dejan Stevanović, Violeta Enea
Focus on Autism and Other Developmental Disabilities.2024; 39(2): 127. CrossRef - Development and validation of the self-injury stigma scale
Caitlin M. O'Loughlin, Kenneth McClure, Brooke A. Ammerman
Journal of Psychiatric Research.2024; 173: 48. CrossRef - Exploring perceived oppressiveness of high-rise window views: A virtual reality assessment of planning measures and visual elements' influence
Fei Wang, Jun Munakata
Journal of Building Engineering.2024; 96: 110476. CrossRef - Swedish teacher conceptions of assessment: a focus on improving outcomes
Gavin T. L. Brown, Catarina Andersson, Mikael Winberg, Björn Palmberg, Torulf Palm
Education Inquiry.2024; : 1. CrossRef - Öğretmenlerin Örgütsel Adalet Algısı, İşten Ayrılma Niyeti Algısı ve Öznel İyi Oluşları Arasındaki İlişki
Ahmet Kılıç, Bahri Aydın
Türk Eğitim Bilimleri Dergisi.2024; 22(1): 384. CrossRef - Knowledge, attitude and practice of healthcare providers on mistreatment of women during labour and childbirth: A cross-sectional study in Tehran, Iran, 2021
Marjan Mirzania, Elham Shakibazadeh, Meghan A. Bohren, Farah Babaey, Sedigheh Hantoushzadeh, Abdoljavad Khajavi, Abbas Rahimi Foroushani, Fereshteh Behmanesh
PLOS ONE.2024; 19(10): e0311346. CrossRef - Work-leisure conflict and emotional labor in hospitality: a moderated-mediation model
Shih-Hao Liu
The Service Industries Journal.2024; 44(13-14): 970. CrossRef - The Assessment of Practice Quality–Mindfulness (PQ-M): Translation and Psychometric Properties in Chinese Population
Yanping Wei, Wentao Xiao, Fangfang Chi, Yifei Xu, Limin Sun, Qing Zhong, Jiang Xue, Shulin Chen
Mindfulness.2024; 15(5): 1109. CrossRef - Quantitative Analysis of Different Foveal Avascular Zone Metrics in Healthy and Diabetic Subjects
Ouafa Sijilmassi
Diabetology.2024; 5(3): 246. CrossRef - Not all information is informative: An exploration of educational content on recycled potable water knowledge and acceptance
Braden Tanner, Portia McDonald, Dana Mahmoud-Elhaj, David Sabatini, Jim F. Chamberlain, Anisha Nijhawan, Eleanor Rainbolt-Forbes, Adam Feltz
Water Research.2024; 252: 121254. CrossRef - Vitality and learning: the impact of mobile technology use across work–nonwork boundaries on job performance
Mi Zhou, Wei Liu, Weiguo Fan
Behaviour & Information Technology.2024; 43(12): 2907. CrossRef - Optimizing quality enhancement cells in higher education institutions: analyzing management support, quality infrastructure and staff training
Shahzaf Iqbal, Kamran Moosa, Che Azlan Bin Taib
International Journal of Quality & Reliability Management.2024; 41(6): 1572. CrossRef - Utilitarian ethics: the impact of the dark tetrad traits and the mechanisms of moral disengagement
D. S. Kornienko, М. V. Baleva, N. P. Yachmenyova
Psikhologicheskii zhurnal.2024;[Epub] CrossRef - A Mobile Instant Messaging–Delivered Psychoeducational Intervention for Cancer Caregivers
Qinqin Cheng, Marques Shek Nam Ng, Kai Chow Choi, Yongyi Chen, Gaoming Liu, Winnie Kwok Wei So
JAMA Network Open.2024; 7(2): e2356522. CrossRef - The Associations Between the Problematic Social Media and Smartphone Use, Social Phobia, and Self-Esteem: A Structural Equation Modeling Analysis
Paolo Soraci, Renato Pisanti, Rocco Servidio, Alex J. Holte, Ambra Ferrari, Zsolt Demetrovics, Mark D. Griffiths
International Journal of Mental Health and Addiction.2024;[Epub] CrossRef - The Single-Matrix Digit Cancellation Test, a Screener for Selective Attention Deficits: Standardization in an Italian Population Sample and Clinical Usability in Acute Stroke Patients
Fabrizio Pasotti, Edoardo Nicolò Aiello, Alessandra Bollani, Matteo Querzola, Sara Cozzi, Francesca Manfrin, Stefania Bruno, Barbara Poletti, Nicola Ticozzi, Vincenzo Silani, Gabriella Bottini
Cerebrovascular Diseases.2024; 53(1): 62. CrossRef - Linking Perfectionism with Moral Behaviors in Sport: The Mediating Role of Burnout and Moral Disengagement
Nicholas Stanger, Gareth E. Jowett, Mariana Kaiseler, Toni L. Williams
Research Quarterly for Exercise and Sport.2024; 95(3): 646. CrossRef - The Breastfeeding Self-Efficacy Scale–Short Form (BSES-SF): German Translation and Psychometric Assessment
Linda Maurer, Anna Schultz, Cindy-Lee Dennis, Rainer W. Alexandrowicz, Karen McQueen
Journal of Human Lactation.2024; 40(3): 374. CrossRef - Does Transactional Leadership Generate Work Engagement in the Hotel Industry? The Role of Motivating Language and Job Prestige
Md Karim Rabiul
Journal of Quality Assurance in Hospitality & Tourism.2024; 25(3): 442. CrossRef - Early Detection of Depression in Parkinson’s Disease: Psychometrics and Diagnostics of the Spanish Version of the Beck Depression Inventory
Alfonsina D’Iorio, Gianpaolo Maggi, Pasqualina Guida, Edoardo Nicolò Aiello, Barbara Poletti, Vincenzo Silani, Nicola Ticozzi, Gabriella Santangelo, Ignacio Obeso
Archives of Clinical Neuropsychology.2024; 39(4): 418. CrossRef - Enhancing the development and understanding of assessment literacy in higher education
Xiaotong Zhu, Carol Evans
European Journal of Higher Education.2024; 14(1): 80. CrossRef - Transactional stress-coping configurations in nature-based tourism destinations
Peizhe Li, Xiao Xiao, Evan Jordan, Honglei Zhang, Jie Gao
Tourism Management Perspectives.2024; 51: 101240. CrossRef - Cognitive heterogeneity in Attention Deficit Hyperactivity Disorder: Implications for maths
Margarita Kanevski, Josie N. Booth, Tracy M. Stewart, Sinead M. Rhodes
British Journal of Developmental Psychology.2024; 42(4): 596. CrossRef - Growth, yield and quality variability of flue-cured tobacco in response to soil and climatic factors in Northern Vietnam
Dung Tien Nghiem, Hang Thi Thuy Vu, Ninh Van Nguyen, Cham Thi Tuyet Le
Italian Journal of Agronomy.2024; 19(3): 100016. CrossRef - The mediating role of parenting sense of competence on the relationship between social support and postnatal depressive symptoms
Min Guo, Min Kong, Wen-Xin Shi, Shi-Jia Qin, Yin-Ping Zhang
Current Psychology.2024; 43(19): 17282. CrossRef - Self-inefficacy's impact on well-being indices in students self-identifying with cluttering characteristics
Gil Zukerman, Michal Icht, Avi Zigdon, Liat Korn
Journal of Communication Disorders.2024; 112: 106469. CrossRef - Evaluating Mental Health Literacy among Iranian Women: A Cross-Sectional Study
Rahim Jafari, Saeedeh Zenoozian, Khadijeh Hajimiri
Journal of Human Environment and Health Promotion.2024; 10(2): 89. CrossRef - Turkish reliability and validity study of Barkley’s BAARS-IV self-report current symptoms
Tansu Eda Topaloglu, Bilge Dogan, Doga Sevincok, Levent Sevincok
Middle East Current Psychiatry.2024;[Epub] CrossRef - Mental health and burnout during medical school: Longitudinal evolution and covariates
Valerie Carrard, Sylvie Berney, Céline Bourquin, Setareh Ranjbar, Enrique Castelao, Katja Schlegel, Jacques Gaume, Pierre-Alexandre Bart, Marianne Schmid Mast, Martin Preisig, Alexandre Berney, Santiago Gascón
PLOS ONE.2024; 19(4): e0295100. CrossRef - Plasma metabolites of a healthy lifestyle in relation to mortality and longevity: Four prospective US cohort studies
Anne-Julie Tessier, Fenglei Wang, Liming Liang, Clemens Wittenbecher, Danielle E. Haslam, A. Heather Eliassen, Deirdre K. Tobias, Jun Li, Oana A. Zeleznik, Alberto Ascherio, Qi Sun, Meir J. Stampfer, Francine Grodstein, Kathryn M. Rexrode, JoAnn E. Manson
Med.2024; 5(3): 224. CrossRef - Validation of the Greek Warwick-Edinburgh Mental Well-Being Scale (WEMWBS) in a Mature Student Community-Based Sample
Konstantinos Petrogiannis, Irina Sangeorzan, Panoraia Andriopoulou
Adversity and Resilience Science.2024; 5(4): 351. CrossRef - Positive psychological interventions on alcohol use and consequences: Pilot randomized trial in a young adult cannabis-using sample
Catherine D. Trinh, Rachel Girard, Melissa R. Schick, Nichea S. Spillane
Journal of Substance Use and Addiction Treatment.2024; 158: 209241. CrossRef - Social disorganization theory and the college campus periphery
Mike Tapia, Erika Ochoa, Kelsey Cundiff
Social Science Quarterly.2024; 105(7): 2054. CrossRef - Religiosity, internalized sexism, and sexual attitudes in late female adolescents: A structural equality modeling
Mahmut Evli
Adıyaman Üniversitesi Sağlık Bilimleri Dergisi.2024; 10(3): 246. CrossRef - Precision Nutrient and Soil Tillage Management for Sustainable Winter Barley Production (Hordeum vulgare L.) and Tillage Impact on Soil CO2 Emission
Amare Assefa Bogale, Zoltan Kende, Akos Tarnawa, Peter Miko, Marta Birkás, Gergő Péter Kovács, Attila Percze
Agronomy.2024; 15(1): 2. CrossRef - Peer Interaction Dynamics and Second Language Learning Trajectories During Study Abroad: A Longitudinal Investigation Using Dynamic Computational Social Network Analysis
Michał B. Paradowski, Nicole Whitby, Michał Czuba, Piotr Bródka
Language Learning.2024; 74(S2): 58. CrossRef - IMPACT OF SUSTAINABLE SUPPLY CHAIN IN GHANA'S PHARMACEUTICAL SECTOR ON UPSTREAM PHARMACEUTICAL INDUSTRY
Albert Tchey Agbenyegah, Gifty Kumadey
Journal of Law and Sustainable Development.2024; 12(8): e3808. CrossRef - The role of psychosocial factors and biological sex on rural Thai adolescents' drinking intention and behaviours: A structural equation model
Eakachai Kantawong, Tsui‐Sui Annie Kao, Lorraine B. Robbins, Jiying Ling, Kaston D. Anderson‐Carpenter
Journal of Advanced Nursing.2024; 80(4): 1393. CrossRef - Buyer–supplier collaboration's commitment. An antecedent for procurement performance of large manufacturing entities in Tanzania
Honest F. Kimario, Leonada R. Mwagike
Benchmarking: An International Journal.2024; 31(2): 535. CrossRef - Factors That Influence the Tenure of Direct Support Professionals in New York State Provider Agencies
Hirah A. Mir, Qingyang Liu, Oxana Rosca, Emily Blakeslee
Intellectual and Developmental Disabilities.2024; 62(1): 14. CrossRef - Wives with long and high-quality hair have more frequent sex
Jeong Eun Cheon, Jeongwoo John Kim, Young-Hoon Kim
Frontiers in Psychology.2024;[Epub] CrossRef - Cerebellar tDCS combined with augmented reality treadmill for freezing of gait in Parkinson’s disease: a randomized controlled trial
Fabrizio Pisano, Denise Mellace, Ambra Fugatti, Edoardo Nicolò Aiello, Silvia Diotti, Beatrice Curti, Alessandra Giust, Angelica Marfoli, Cecilia Perin, Angelica De Sandi, Dario Alimonti, Alberto Priori, Roberta Ferrucci
Journal of NeuroEngineering and Rehabilitation.2024;[Epub] CrossRef - A Novel Framework for the Study of Culturally Evolved Chivalric Disposition in Multiple Social Science Applications
Matthew Muscat-ınglott
Uluslararası Kültürel ve Sosyal Araştırmalar Dergisi (UKSAD).2024;[Epub] CrossRef - Who’s to blame? How subtle negative messages about outgroups contribute to ethnic prejudice development in middle to late childhood
Daudi van Veen, Rosanneke A.G. Emmen, Judi Mesman
Applied Developmental Science.2024; : 1. CrossRef - The impacts of transformational leadership on emotional labour in Taiwanese private nonprofit long-term care institutions: the mediating role of psychological contract
Chih-Jou Chen, Pei-Hsuan Tsai, Ju-Chuan Wu
Asia Pacific Business Review.2024; 30(4): 691. CrossRef - DETERMINING THE EFFECT OF HEALTH CARE MARKETING MIX ELEMENTS ON OBTAINING HEALTH INFORMATION IN THE DIGITAL ENVIRONMENT
Muhammet Salih Yiğit, Murat Başal
Akademik Hassasiyetler.2024; 11(26): 194. CrossRef - Mental Health Treatment-Seeking Appraisal, Afrocentric Cultural Norms, and Mental Health Functioning: Buffering Factors of Young Black Men’s Externalizing Behavior
Husain Lateef, Leslie Adams, Donte Bernard, Francine Jellesma, Melody Rachel Konadu Frempong, Baffour Boaten Boahen-Boaten, Benjamin C. B. Leach, Ellie Borgstrom, Portia B. Nartey
Journal of Racial and Ethnic Health Disparities.2024; 11(5): 3150. CrossRef - An examination of accessibility and use of critical thinking for minority and disadvantaged students
Maree J. Davies, Simon Esling, Shengnan Wang
Thinking Skills and Creativity.2024; 53: 101564. CrossRef - Sustainable entrepreneurship in tourism: The interaction between tourism enterprise and community
Xinying Zeng, Yaoqi Li, Chun Zhang, Xueru Yang
Journal of Hospitality and Tourism Management.2024; 60: 429. CrossRef - The influence of perceived authenticity on pilgrimage image in the Dajia Mazu pilgrimage
Yung-Chuan Huang, Yi Hsien Lin
Current Issues in Tourism.2024; 27(12): 1989. CrossRef - Development of main concept and core lexicon checklists for the original and modern Cookie Theft stimuli
Sarah Grace Dalton, Mohammed AL Harbi, Shauna Berube, H. Isabel Hubbard
Aphasiology.2024; 38(12): 1975. CrossRef - Can spiritual well-being help people be satisfied with singlehood? Exploring the temporal link between spiritual well-being and satisfaction with singlehood
Katarzyna Adamczyk, Agnieszka Ewa Łyś, Radosław Trepanowski
Journal of Spirituality in Mental Health.2024; 26(4): 349. CrossRef - ChatGPT’s crystal ring: simulating auditors’ use of machine learning in stock price prediction
Omar Arabiat, Hashem Alshurafat
Journal of Decision Systems.2024; : 1. CrossRef - Measuring design mindset: developing the Design Mindset Inventory through its relationship with ambiguity tolerance, self-efficacy and sensation-seeking
Jakob Clemen Lavrsen, Claus-Christian Carbon, Jaap Daalhuizen
Design Science.2024;[Epub] CrossRef - Patient-reported questionnaires to preoperatively identify high-risk surgical patients
Renske Meijer, David W. G. ten Cate, Bart C. Bongers, Marta Regis, Hans H. C. M. Savelberg, Gerrit D. Slooter, Stef Janssen, Martijn van Hooff, Goof Schep
Langenbeck's Archives of Surgery.2024;[Epub] CrossRef - The Bergen–Yale Sexual Addiction Scale (BYSAS): Longitudinal Measurement Invariance Across a Two-Year Interval
Rapson Gomez, Taylor Brown, Vasileios Stavropoulos
Psychiatric Quarterly.2024; 95(4): 561. CrossRef - Perceived clinical competence and its related factors among registered nurses employed at selected outpatient clinics in Egypt
Rasha A. Mohamed, Mohammed Fayez J. Alharbi, Rahmah Aloufi, Nisha Abraham, Nagwa Nabeh Taref, Eman Samy Bauomy, Safa H. Alkalash, Marzouk M. Marzouk, Abeer A. Almowafy, Ateya Megahed Ibrahim El-eglany
PLOS ONE.2024; 19(12): e0314206. CrossRef - Empowering pro-environmental potential among hotel employees: insights from self-determination theory
Ataul Karim Patwary, S. Mostafa Rasoolimanesh, Mohd Hafiz Hanafiah, Roslizawati Che Aziz, Ahmad Edwin Mohamed, Muhammad Umair Ashraf, Nor Rabiatul Adawiyah Nor Azam
Journal of Hospitality and Tourism Insights.2024; 7(2): 1070. CrossRef - Euthymic despite pain: the role of cognitive reappraisal and experiential avoidance in autoimmune inflammatory rheumatic diseases—a cross-sectional study
Francesco De Vincenzo, Luca Iani, Chiara Alessio, Luca Navarini, Damiano Currado, Annalisa Marino, Anna Contardi
Frontiers in Psychology.2024;[Epub] CrossRef - The insomnia, fatigue, and psychological well‐being of hospital nurses 18 months after the COVID‐19 pandemic began: A cross‐sectional study
Knar Sagherian, Hyeonmi Cho, Linsey M. Steege
Journal of Clinical Nursing.2024; 33(1): 273. CrossRef - Detecting muscle fatigue among community-dwelling senior adults with shape features of the probability density function of sEMG
Jiarui Ou, Na Li, Haoru He, Jiayuan He, Le Zhang, Ning Jiang
Journal of NeuroEngineering and Rehabilitation.2024;[Epub] CrossRef - Elementary School Teachers’ and Counselors’ Decisions on Referring Students for Evaluation: The Impact of ADHD Traits, Achievement, and Giftedness
Avital Tamsut, Hattem Asadi, Gal Nahum Sinai, Noa Saka, Yehuda Pollak
Child Psychiatry & Human Development.2024;[Epub] CrossRef - Enhancing student satisfaction and academic performance through school courtyard design: a quantitative analysis
Muna Salameh, Basim Touqan, Abubakr Suliman
Architectural Engineering and Design Management.2024; 20(4): 911. CrossRef - Transforming early-stage firms in emerging countries: Unveiling the power of venture capital; a comparative study of South Africa and Kenya
Ahmed Idi Kato, Germinah Evelyn Chiloane-Tsoka
Cogent Business & Management.2024;[Epub] CrossRef - Socioformative pedagogical practices and academic performance in students: Mediation of socioemotional skills
Sergio Tobon, Edgar Fidel Lozano-Salmorán
Heliyon.2024; 10(15): e34898. CrossRef - Callous–Unemotional Traits and Conduct Problems in Children: The Role of Strength and Positive Characteristics
Patrícia Figueiredo, Andreia Azeredo, Ricardo Barroso, Fernando Barbosa
Behavioral Sciences.2024; 14(7): 609. CrossRef - Mediating role of physician’s empathy between physician’s communication and patient’s satisfaction
Maham Arshad, Shyamkumar Sriram, Saira Khan, Pavan Kumar Gollapalli, Muayad Albadrani
Journal of Family Medicine and Primary Care.2024; 13(4): 1530. CrossRef - The relationship between childhood psychological abuse and depression in college students: a moderated mediation model
Yang Liu, Qingxin Shen, Liangfan Duan, Lei Xu, Yongxiang Xiao, Tiancheng Zhang
BMC Psychiatry.2024;[Epub] CrossRef - The Relationship between Learning Outcomes and Graduate Competences: The Chain-Mediating Roles of Project-Based Learning and Assessment Strategies
Ming Li, Mohd Isa Rohayati
Sustainability.2024; 16(14): 6080. CrossRef - Rice Classification and Quality Detection Success with Artificial Intelligence Technologies
Gökalp Çınarer, Nizamettin Erbaş, Abdurrahman Öcal
Brazilian Archives of Biology and Technology.2024;[Epub] CrossRef - Ubuntu leadership as a predictor of employee engagement: A South African study
Kerushan Chetty, Gavin Price
SA Journal of Human Resource Management.2024;[Epub] CrossRef - L2 skill-specific anxiety and communication apprehension: the role of extramural English in the Turkish context
Mehmet Sercan Uztosun, Muhammed Kök
Innovation in Language Learning and Teaching.2024; 18(1): 17. CrossRef - The gender congruence and life satisfaction scale for transgender and gender-diverse youth (GCLS-Y): a validation study with samples from the UK and US
Bethany A. Jones, Alisha. L. Nguyen, Gina M. Sequeira, Shane D. Morrison, Liam Cahill
International Journal of Transgender Health.2024; : 1. CrossRef - The Asymmetric Moderating Role of Intolerance of Uncertainty in the Longitudinal Reciprocal Associations between Sleep Disturbance and Internalizing Symptoms: A Two-wave Study among 54,240 Adolescents
Haoxian Ye, Yixin Liu, Zifan Cai, Nan Jiang, Sisi He, Wanqing Yu, Ruixin Zhao, Tengfei Cheng, Dongfang Wang, Fang Fan
International Journal of Mental Health and Addiction.2024;[Epub] CrossRef - Past reflection and future selection: A study of green hotel choices
Xinying Zeng, Anna Kralj, Rawan Nimri, Yaoqi Li
International Journal of Hospitality Management.2024; 122: 103880. CrossRef - White matter integrity of right frontostriatal circuit predicts internet addiction severity among internet gamers
Hui Zhou, Liangyu Gong, Conghui Su, Binyu Teng, Wan Xi, Xiumei Li, Fengji Geng, Yuzheng Hu
Addiction Biology.2024;[Epub] CrossRef - Trajectories of Self-Control in Emerging Adulthood: Implications for Academic, Psychological, and Career Development among Chinese College Students
Cong Yi, Jun Wei, Yonghe Ti, Jian-Bin Li
Applied Research in Quality of Life.2024; 19(2): 641. CrossRef - Information literacy skills of health professions students in assessing YouTube medical education content
Orianne Pearlman, Lynda Tierney Konecny, Matthew Cole
Frontiers in Education.2024;[Epub] CrossRef - Assessing effects of facade characteristics and visual elements on perceived oppressiveness in high-rise window views via virtual reality
Fei Wang, Jun Munakata
Building and Environment.2024; 266: 112043. CrossRef - Consumption Trends and Eating Context of Lentils and Dried Peas in the United States: A Nationally Representative Study
Namrata Sanjeevi, Pablo Monsivais
Nutrients.2024; 16(2): 277. CrossRef - The impact of an exercise and sport intervention on cognitive function and pain among forcibly displaced individuals at risk for PTSD: a secondary analysis of the SALEEM randomized controlled trial
Florian Knappe, Konstantinia Filippou, Antonis Hatzigeorgiadis, Ioannis D. Morres, Sebastian Ludyga, Harald Seelig, Emmanouil Tzormpatzakis, Elsa Havas, Yannis Theodorakis, Roland von Känel, Uwe Pühse, Markus Gerber
BMC Medicine.2024;[Epub] CrossRef - Splash of body fluids among healthcare support staff in Ghana: a cross-sectional study
Philip Apraku Tawiah, Emmanuel Appiah-Brempong, Paul Okyere, Mary Eyram Ashinyo
SAGE Open Medicine.2024;[Epub] CrossRef - Effects of Childcare Hands-On Gardening on Preschoolers’ (3–5 Years) Physical Activity in Semi-Arid Climate Zone
Muntazar Monsur, Tristen Hefner, Jason Van Allen, Nazia Afrin Trina, S. Y. Andalib, Nilda Cosco
International Journal of Environmental Research and Public Health.2024; 21(5): 548. CrossRef - A new robust ridge parameter estimator having no outlier and ensuring normality for linear regression model
Selman Mermi, Özge Akkuş, Atila Göktaş, Necla Gündüz
Journal of Radiation Research and Applied Sciences.2024; 17(1): 100788. CrossRef - Ethnic representation and stereotypes in mathematics and Dutch language textbooks from the Netherlands
Daudi van Veen, Rosanneke A. G. Emmen, Tessa M. van de Rozenberg, Judi Mesman
Whiteness and Education.2024; 9(2): 270. CrossRef - Decoding algorithm appreciation: Unveiling the impact of familiarity with algorithms, tasks, and algorithm performance
Hasan Mahmud, A.K.M. Najmul Islam, Xin (Robert) Luo, Patrick Mikalef
Decision Support Systems.2024; 179: 114168. CrossRef - Cross-validating the measurement scale for consumers’ experience with hospitality and tourism technology: a multi-sector approach
Hyejo Hailey Shin, Kevin Kam Fung So, Miyoung Jeong
International Journal of Contemporary Hospitality Management.2024; 36(12): 4215. CrossRef - Academic stress, self-esteem and nonsuicidal self-injury among adolescents: The moderating effect of the oxytocin receptor (OXTR) gene rs53576 polymorphism
Pei Chen, Guo-Dong Wang, Cheng-Fu Yu, Yan-Gang Nie
Current Psychology.2024; 43(5): 4728. CrossRef - Nursing students’ evaluation of clinical placement education quality: A national database analysis
Colleen Ryan, Areum Hyun, Lynda Hughes, Fiona Bogossian, Simon Cooper
Nurse Education in Practice.2024; 81: 104185. CrossRef - Healthcare experiences among adults with hypermobile Ehlers-Danlos syndrome and hypermobility spectrum disorder in the United States
Emma Estrella, Patricia A. Frazier
Disability and Rehabilitation.2024; 46(4): 731. CrossRef - A latent profiling approach to foreign language enjoyment and L2 achievement
Minjuan Gao
Journal of Multilingual and Multicultural Development.2024; : 1. CrossRef - A practical test for retronasal odor identification based on aromatized tablets
Michal Pieniak, Can Tutar, Wiktoria Jedryczka, Hakim Benkhatar, Veronique Debroise Blanchard-Dignac, Antje Haehner, Thomas Hummel
Journal of Neuroscience Methods.2024; 406: 110135. CrossRef - Who Learns from Reading Texts in General Chemistry?
René W. Buell, Samuel Pazicni
Education Sciences.2024; 14(12): 1287. CrossRef - Ảnh hưởng của động cơ vay, nhận thức về lợi ích và rủi ro đối với ý định sử dụng dịch vụ cho vay ngang hàng của sinh viên đại học tại Việt Nam
Hưng Nguyễn Thành
Tạp chí Khoa học Thương mại.2024; : 91. CrossRef - Measuring incompleteness and not just right experiences: A psychometric evaluation of two commonly used questionnaires in OCD and anxiety disorders samples
Christina Puccinelli, Karen Rowa, Laura J. Summerfeldt, Randi E. McCabe
Journal of Obsessive-Compulsive and Related Disorders.2024; 43: 100916. CrossRef - How to detect affect recognition alterations in amyotrophic lateral sclerosis
Veronica Castelnovo, Elisa Canu, Edoardo Nicolò Aiello, Beatrice Curti, Elisa Sibilla, Silvia Torre, Fabiola Freri, Chiara Tripodi, Laura Lumaca, Edoardo Gioele Spinelli, Paride Schito, Tommaso Russo, Yuri Falzone, Federico Verde, Vincenzo Silani, Nicola
Journal of Neurology.2024; 271(11): 7208. CrossRef - Effect of Emotional Intelligence and Critical Thinking Disposition on Resilience of the Student in Transition to Higher Education Phase
Sahanowas Sk, Santoshi Halder
Journal of College Student Retention: Research, Theory & Practice.2024; 25(4): 913. CrossRef - Effects of health-related dispositions on citizens’ appraisals toward the COVID-19 pandemic and protective behavior
Xinyuan Fu, Ruoran Fu, Shuxian Li, Xiaona Du, Mei Zhang, Jiaxin Duan, Hanmin Wang, Guixin Li, Ted C. T. Fong
PLOS ONE.2024; 19(9): e0305995. CrossRef - Subjective norms towards entrepreneurship and Malaysian students’ entrepreneurial intentions: does gender matter?
Jia Wei Chin, Michael J Mustafa, Melati Nungsari
Asia Pacific Journal of Innovation and Entrepreneurship.2024; 18(2): 195. CrossRef - Kurumsal İtibar, Marka Güveni ve Marka Sadakati Kavramlarına Yönelik Bir Araştırma
Emel Karayel Bilbil, Sevda Orha Hazar
Selçuk İletişim.2024; 17(1): 100. CrossRef - Applying work measurements to identify productivity potentials: the case of prefabricated concrete elements
Søren Munch Lindhard
International Journal of Construction Management.2024; 24(15): 1668. CrossRef - From clicks to credits: examining the influence of online engagement and internet addiction on academic performance in Chinese universities
Yongzhong Jiang, Dirgha Raj Joshi, Jeevan Khanal
International Journal of Educational Technology in Higher Education.2024;[Epub] CrossRef - Developing dynamic capabilities for successful digital transformation projects: the mediating role of change management
Nizar Abdulwahab Ali Al-Moaid, Senan Ghaleb Almarhdi
Journal of Innovation and Entrepreneurship.2024;[Epub] CrossRef - Role of Demographic Factors on Academic Motivation of Medical Students in a Malaysian Private University
Malaysian Journal of Medicine and Health Sciences.2024; 20(1): 212. CrossRef - The effectiveness of a training program on perceptions of caring culture among Turkish nurses: A quasi‐experimental trial
Mehmet Gülşen, Adalet Kutlu
International Nursing Review.2024; 71(1): 122. CrossRef - Whether English Proficiency and English Self-Efficacy Influence the Credibility of ChatGPT-Generated English Content of EMI Students
Duong Thi Thuy Mai, Nguyen Van Hanh
International Journal of Computer-Assisted Language Learning and Teaching.2024; 14(1): 1. CrossRef - Factor structure and psychometric properties of the Jordanian version of the depression anxiety stress scale (DASS‐21)
Khaled A. Al‐Dassean, Odeh S. Murad
Neuropsychopharmacology Reports.2024; 44(2): 447. CrossRef - Comparison of perceived masticatory ability in completely edentulous patients treated with thermoplastic complete denture versus single implant-retained mandibular overdenture: a single-center prospective observational study
Mostafa I. Fayad, Ihab I. Mahmoud, Ahmed Atef Aly Shon, Mohamed Omar Elboraey, Ramy M. Bakr, Rania Moussa
PeerJ.2024; 12: e17670. CrossRef - Social networking usage and mental health problems in the Kurdistan region of Iraq during the COVID-19 outbreak and lockdown
Dyari S. Hama amin, Parzheen J. Mohammad
Discover Psychology.2024;[Epub] CrossRef - Ruminative thinking mediates the effects of exposure to adverse life events on psychotic-like experiences
Leonardo Fazio, Alessandra Raio, Tobias Banaschewski, Arun L. W. Bokde, Sylvane Desrivières, Herta Flor, Hugh Garavan, Penny Gowland, Antoine Grigis, Andreas Heinz, Jean-Luc Martinot, Marie-Laure Paillère Martinot, Eric Artiges, Frauke Nees, Dimitri Papad
Frontiers in Psychology.2024;[Epub] CrossRef - The dose-dependent effect of caffeine supplementation on performance, reaction time and postural stability in CrossFit – a randomized placebo-controlled crossover trial
Natalia Główka, Jakub Malik, Tomasz Podgórski, Rafał Stemplewski, Janusz Maciaszek, Julia Ciążyńska, Emilia E. Zawieja, Agata Chmurzynska, Paulina M. Nowaczyk, Krzysztof Durkalec-Michalski
Journal of the International Society of Sports Nutrition.2024;[Epub] CrossRef - Autonomy, self-realization, and psychological empowerment: a prospective mixed methods study of the effects of residential immersive life skills programs for youth with physical disabilities
Gillian King, Shauna Kingsnorth, Amy C. McPherson, Diana Tajik-Parvinchi
Disability and Rehabilitation.2024; 46(14): 3097. CrossRef - RESEARCH ON THE RELATIONSHIP BETWEEN HEALTH LITERACY AND ORGAN DONATION
Durmuş Gökkaya, İbrahim Hüseyin Cansever, Mesut Karaman, Osman Şenol
Pamukkale University Journal of Social Sciences Institute.2024;[Epub] CrossRef - Does botulinum toxin affect psycho-social aspects in dystonia?
Angelica Marfoli, Francesca Mameli, Edoardo Nicolò Aiello, Fabiana Ruggiero, Angelica De Sandi, Denise Mellace, Beatrice Curti, Roberto Vimercati, Barbara Poletti, Nicola Ticozzi, Daniela Chieffo, Gabriella Santangelo, Sergio Barbieri, Alberto Priori, Rob
Journal of Neural Transmission.2024; 131(8): 953. CrossRef - Promoting social inclusion for adult communities: The moderating role of leisure constraints on life satisfaction in five European countries
Funda Koçak, Bülent Gürbüz
Journal of Community & Applied Social Psychology.2024;[Epub] CrossRef - Exploring relationship satisfaction in mothers of children with disabilities: the predictive role of interparental conflicts and moderating role of dyadic coping
Marijana Vrankić Pavon, Ana Wagner Jakab, Ajana Löw
Frontiers in Psychiatry.2024;[Epub] CrossRef - Evaluating the Effect of TeamSTEPPS on Teamwork Perceptions and Patient Safety Culture among Newly Graduated Nurses
Asmaa Elwan Hassan, Faten Ahmed Mohammed, Abeer Mohamed Zakaria, Ibrahim Abdullatif Ibrahim
BMC Nursing.2024;[Epub] CrossRef - An examination of an inclusive French immersion program and preschoolers' executive functioning skills
Michele Regalla, Hilal Peker, Marisa Macy
Foreign Language Annals.2024; 57(4): 1000. CrossRef - Rural Homestay Experiencescape: Scale Development and Its Emotional and Cognitive Paths to Guest Engagement Behavior
Huawen Shen, Yilin Hu, Daisy X.F. Fan, Dimitrios Buhalis
Journal of Hospitality & Tourism Research.2024;[Epub] CrossRef - Assessment of Surgical Difficulty in Patients with Rectal Cancer—The Impact of Pelvimetry
João Stuart, Pedro Miguel Dias dos Santos, Carlos Costa Pereira, Sandra F. Martins
International Journal of Translational Medicine.2024; 4(1): 163. CrossRef - Developing a short language classroom engagement scale (LCES) and linking it with needs satisfaction and achievement
Liu Eerdemutu, Jean-Marc Dewaele, Junju Wang
System.2024; 120: 103189. CrossRef - Normality tests for statistical analysis in dentistry: A brief notes for researcher
Mohamad Shafiq Mohd Ibrahim
IIUM Journal of Orofacial and Health Sciences.2024; 5(1): 1. CrossRef - Differing effectiveness of transcranial random noise stimulation and transcranial direct current stimulation for enhancing working memory in healthy individuals: a randomized controlled trial
Yukina Tokikuni, Akihiro Watanabe, Hisato Nakazono, Hiroshi Miura, Ryuji Saito, Duan Miaowen, Kanako Fuyama, Keita Takahashi, Kazufumi Okada, Kazuhiro Sugawara, Harukazu Tohyama, Susumu Yoshida, Kenneth N. K. Fong, Daisuke Sawamura
Journal of NeuroEngineering and Rehabilitation.2024;[Epub] CrossRef - Frontotemporal-spectrum disorders and functional independence in non-demented ALS patients
Edoardo Nicolò Aiello, Federica Solca, Silvia Torre, Francesco Gentile, Francesco Scheveger, Marco Olivero, Eleonora Colombo, Alessio Maranzano, Martina Manzoni, Claudia Morelli, Alberto Doretti, Federico Verde, Vincenzo Silani, Nicola Ticozzi, Barbara Po
Neurological Sciences.2024; 45(3): 1087. CrossRef - Safety climate in Pakistani universities’ laboratories: an assessment of individual factors
Tufail Ahmed, Mirza Jahanzaib, Muhammad Asad Ali, Muhammad Huzaifa Raza, Muhammad Jawad, Sadaf Zahoor
International Journal of Occupational Safety and Ergonomics.2024; 30(2): 330. CrossRef - Examining the Relationship Between Health Perception and Preoperative Anxiety in Surgical Patients
Özlem Şahin Akboğa, Yurdagül Günaydın, Esra Arıca Özbudak
Journal of Education and Community Health.2024; 11(2): 83. CrossRef - The Mediating Effects of Extended Family Support and Relationship Change on Romantic Bonding and Support in Romantic Relationship Among Incarcerated Men
Eman Tadros, Khoi Nguyen Anh Le
Victims & Offenders.2024; : 1. CrossRef - Lifetime and current mental health based on avoidant/restrictive food intake disorder history versus other eating disorder history in the Healthy Minds Study
Brianne N. Richson, Hana F. Zickgraf
International Journal of Eating Disorders.2024; 57(10): 1999. CrossRef - Relationships between childhood adversity and life functioning in US college students: Risk and resilience
Addie N. Merians, Emily Mischel, Patricia Frazier, Katherine Lust
Journal of American College Health.2024; 72(1): 71. CrossRef - Social and behavior change communication competency among front-line healthcare system actors in Ethiopia: a cross-sectional study
Simegnew Handebo, Rachana Sharma, Tesfaye Simireta, Hailemariam Addissie, Getnet Bayih Endalew, Eshetu Girma, Kenzudin Assfa Mossa
BMC Public Health.2024;[Epub] CrossRef - Antrenörlerin Zihinsel Yetersizliği Olan Bireylerde Sporun Etkilerine Yönelik Farkındalık Düzeyleri
Ekrem Levent İlhan, Necip Arman
Herkes için Spor ve Rekreasyon Dergisi.2024; 6(1): 16. CrossRef - Purpose in life, loneliness and depression among patients with substance use disorders in the psychiatric hospitals in Ghana
Anthony Kwabena Nkyi, Jerry Paul K. Ninnoni, Meghana Ray
PLOS ONE.2024; 19(4): e0299391. CrossRef - The Indirect Effects of Fathers’ Parenting Style and Parent Emotion Regulation on the Relationship Between Father Self-Efficacy and Children’s Mental Health Difficulties
Alicia Carbone, Carmela Pestell, Thom Nevill, Vincent Mancini
International Journal of Environmental Research and Public Health.2024; 22(1): 11. CrossRef - Biometric description of 34 589 eyes undergoing cataract surgery: sex differences
Marta Jiménez-García, Francisco J. Segura-Calvo, Martín Puzo, Francisco J. Castro-Alonso
Journal of Cataract & Refractive Surgery.2024; 50(7): 668. CrossRef - Death Obsession, COVID-19–Related Fear and Religiosity in People Living with Type 2 Diabetes
Violeta Enea, Octav Sorin Candel, Simona Alexandra Zancu, Alexandra Maftei, Livia Bîrlădeanu, Daniel Timofte
OMEGA - Journal of Death and Dying.2024; 89(3): 1094. CrossRef - The Association between Mindful Parenting, and Internalizing and Externalizing Symptoms in Adolescence
Estíbaliz Royuela-Colomer, Izaskun Orue, Laura Visu-Petra, Liria Fernández-González
Journal of Child and Family Studies.2024; 33(6): 1844. CrossRef - Effects of Neuropilates on Functional Outcomes in Chronic Stroke: A Randomized Clinical Trial
Cristina García-Bravo, Laura Delgado-Lobete, Rebeca Montes-Montes, Mª Pilar Rodríguez-Pérez, Nuria Trugeda-Pedrajo, Gemma Fernández-Gómez, Sara García-Bravo
Healthcare.2024; 12(8): 850. CrossRef - Understanding value in residents’ experiences and its impact on life satisfaction and value co-creation: empirical evidence from Jiuzhai Valley, China
Yanqin Li, Liangquan Zhang, Jiawei Shi, Chris Ryan
Asia Pacific Journal of Tourism Research.2024; 29(3): 254. CrossRef - Effects of collaborative learning-based food literacy program on healthy eating behavior and hemoglobin A1c among older adults with uncontrolled type 2 diabetes: A randomized controlled trial study in Thailand
Bumnet Saengrut, Sirirat Panuthai, Rojanee Chintanawat, Nattaya Suwankruhasn
Belitung Nursing Journal.2024; 10(5): 498. CrossRef - Crossing Clinical Borders: Anxiety and Depression in U.S. Citizen Children after Parental Deportation or Coercive Relocation
Jaime Fuentes-Balderrama, Guillermina Natera, Fransilvania Callejas, Georgina Miguel-Esponda, Miguel Pinedo, Luis H. Zayas
Adversity and Resilience Science.2024; 5(4): 399. CrossRef - Post-Pandemic Evaluation: Impact of Covid-19 Pandemic on Medical Students’ Mental Health, Self-Esteem, Social Interactions, and Academic Progression in Malaysia
Sia Woon Teen, Tan Jih Huei, Lee Tiong Chan, Tay Jia Chyi
Sage Open.2024;[Epub] CrossRef - Adverse childhood experiences and psychological maladjustment in adolescence: The protective role of epistemic trust, mentalized affectivity, and reflective functioning
Marta Tironi, Simone Charpentier Mora, Marianna Liotti, Alice Fiorini Bincoletto, Annalisa Tanzilli, Donatella Cavanna, Vittorio Lingiardi, Anna Maria Speranza, Guido Giovanardi, Fabiola Bizzi
Journal of Clinical Psychology.2024; 80(11): 2228. CrossRef - A unidimensional short form of the Beck Hopelessness Scale (BHS-7) derived using item response theory
Tyrone B. Pretorius, Anita Padmanabhanunni
Scientific Reports.2024;[Epub] CrossRef - Which Type of Vocabulary-Knowledge Better Correlates with Reading-Comprehension, Meaning-Recognition or Meaning-Recall?
Chihiro Komiya, Stuart McLean
RELC Journal.2024;[Epub] CrossRef - QSM-detected iron accumulation in the cerebellar gray matter is selectively associated with executive dysfunction in non-demented ALS patients
Edoardo Nicolò Aiello, Valeria Elisa Contarino, Giorgio Conte, Federica Solca, Beatrice Curti, Alessio Maranzano, Silvia Torre, Silvia Casale, Alberto Doretti, Eleonora Colombo, Federico Verde, Vincenzo Silani, Chunlei Liu, Claudia Cinnante, Fabio Maria T
Frontiers in Neurology.2024;[Epub] CrossRef - Implicit theories of health predict engagement in healthy lifestyles among Chinese early adolescents: the mediating effect of future self-continuity
Qing Tang, Caixia Jiang, Meng Wang, Yangmei Huang, Jun Wang, Zhangyu Du, Ning Zhang
International Journal of Adolescence and Youth.2024;[Epub] CrossRef - A challenge to the expected: Lack of longitudinal associations between the early caregiving environment, executive functions in toddlerhood, and self‐regulation at 6 years
Lilja K. Jónsdóttir, Tommie Forslund, Matilda A. Frick, Andreas Frick, Emma J. Heeman, Karin C. Brocki
Developmental Science.2024;[Epub] CrossRef - Exploring the Utility of the Rorschach Test in Predicting Weight Loss After Bariatric Surgery
Maíra Stivaleti Colombarolli, Luciano Giromini, Sonia Regina Pasian
Rorschachiana.2024; 45(1): 30. CrossRef - Factor Structure of the Difficulties in Emotion Regulation Scale among Early Adolescents: Results from the Adolescent Brain Cognitive Development Study
Jacqueline E. Smith, Hannah R. Brinkman, Angelo M. DiBello, Jessica L. Hamilton, Teresa M. Leyro, Brianna R. Altman, Samantha G. Farris
Journal of Psychopathology and Behavioral Assessment.2024; 46(2): 580. CrossRef - Does work task motivation mediate the relationship between psychological capital and teacher well-being?
Girum Zewude, Maria Hercz
Psihologija.2024; 57(2): 129. CrossRef - Meta-analysis review for pilot and large-scale constructed wetlands: Design parameters, treatment performance, and influencing factors
Vinh Son Lam, Thi Cuc Phuong Tran, Thi-Dieu-Hien Vo, Dinh Duc Nguyen, Xuan Cuong Nguyen
Science of The Total Environment.2024; 927: 172140. CrossRef - Effects of Gender and Social Network Use on High School Students’ Emotional Well-Being during COVID-19
Sabina Mandić, Neven Ricijaš, Dora Dodig Hundrić
Psychiatry International.2024; 5(2): 154. CrossRef - Effective and ineffective psychological adjustment in breast cancer patients before receiving neoadjuvant chemotherapy: insights from a cohort study
Majid Omari, Salima Kriya, Sara Nadi, Ghita Zerhouni, Chaymae El Abbas, Achraf El Asri, Zineb Benbrahim, Nawfel Mellas, Karima El Rhazi, Mohammed El Amine Ragala, Jaouad El Hilaly, Karima Halim, Lamiae Amaadour, Btissame Zarrouq
BMC Psychology.2024;[Epub] CrossRef - Cross-cultural validation of the Spanish version of the mini cambridge-exeter repetitive thought scale (Mini-CERTS) in two Spanish-speaking populations
Laura Ros, Tom J. Barry, Rigoberto López-Honrubia, Maritza E. Villanueva-Benite, Alberto Morcillo, Jorge J. Ricarte
Transcultural Psychiatry.2024; 61(2): 142. CrossRef - Perceived stress and posttraumatic growth in caregivers of pediatric burn patients undergoing mHealth-enhanced outpatient burn care: A pilot study
Yulia Gavrilova, Emily Rooney, Aaron Lesher
Burns.2024; 50(6): 1682. CrossRef - Marketing halal investment in Jordan: an investigation of Muslims’ behavioral intention to invest in Hajj fund sukuk
Mohammad Nabeel Almrafee
Journal of Islamic Marketing.2024; 15(5): 1350. CrossRef - Evaluation of safety culture factors in the construction industry: a cross-country study of sites
Figen Atasever, Meksut Alev, Serap Tepe, Bulent Mertoglu
International Journal of Occupational Safety and Ergonomics.2024; 30(4): 1143. CrossRef - Effects of a co-designed exercise and sport intervention on cardiorespiratory fitness and metabolic syndrome components among individuals living in a refugee camp in Greece: A randomized controlled trial
Florian Knappe, Konstantinia Filippou, Antonis Hatzigeorgiadis, Ioannis D. Morres, Emmanouil Tzormpatzakis, Elsa Havas, Harald Seelig, Sebastian Ludyga, Flora Colledge, Marianne Meier, Yannis Theodorakis, Roland von Känel, Uwe Pühse, Markus Gerber
Journal of Migration and Health.2024; 9: 100227. CrossRef - Ecological validity of performance-based cognitive screeners in amyotrophic lateral sclerosis: preliminary evidence
Edoardo Nicolò Aiello, Silvia Torre, Federica Solca, Beatrice Curti, Giulia De Luca, Claudia Gendarini, Alessandro Cocuzza, Eleonora Colombo, Alessio Maranzano, Federico Verde, Claudia Morelli, Stefano Messina, Alberto Doretti, Vincenzo Silani, Nicola Tic
Neurological Sciences.2024; 45(11): 5319. CrossRef - Changes in food consumption behavior during the COVID-19 pandemic: a dual process approach on female college students in China
Rongduo Liu, Klaus G. Grunert
British Food Journal.2024; 126(2): 758. CrossRef - Physical activity intention-behavior gap during the COVID-19 pandemic: the moderating role of motivation and health-belief
Jihoon Ahn, Yongse Kim, Dojin Jang
International Journal of Sport and Exercise Psychology.2024; 22(4): 905. CrossRef - Facilitators and Barriers to Pre‐Exposure Prophylaxis Uptake Willingness for Full‐Service Sex Workers: A Social–Ecological Approach
Stephen D. Ramos, Steff Du Bois
Sociological Inquiry.2024; 94(4): 890. CrossRef - The relationship between the Dark Triad and academic burnout mediated by perfectionistic self-presentation
Melissa Klerks, Roberta Dumitrescu, Elien De Caluwé
Acta Psychologica.2024; 250: 104499. CrossRef - Translation, Cross-Cultural Adaptation, and Validation of the Croatian Version of the Athlete Psychological Strain Questionnaire (APSQ)
Katarina Sore, Frane Franic, Luka Androja, Ivana Batarelo Kokic, Darko Marčinko, Stipe Drmic, Zdravko Valentin Markser, Tomislav Franic
Sports.2024; 12(8): 228. CrossRef - Oxygen Saturation Curve Analysis in 2298 Hypoxia Awareness Training Tests of Military Aircrew Members in a Hypobaric Chamber
Manuel Alvear-Catalán, Claudio Montiglio, Danilo Aravena-Nazif, Ginés Viscor, Oscar F. Araneda
Sensors.2024; 24(13): 4168. CrossRef - How well do ridge parameter estimators proposed so far perform in terms of normality, outlier detection, and MSE criteria?
Selman Mermi, Atila Göktaş, Özge Akkuş
Communications in Statistics - Simulation and Computation.2024; : 1. CrossRef - Decent work and work fulfilment: The mediating role of work engagement and the moderating role of psychological ownership
Chantal Olckers, Eileen Koekemoer
Australian Journal of Career Development.2024; 33(3): 242. CrossRef - The relationship between discrimination, alcohol use severity, and PTSD symptoms among Latinx heavy drinkers
Christina S. Lee, Tessa Nalven, Audrey Hai, Miguel Pinedo, Victoria Lopez, Melanie Morris, Jorge Delva, Miguel Cano
Journal of Substance Use and Addiction Treatment.2024; 159: 209263. CrossRef - Spiritual Seeking dan Flourishing Mahasiswa Seminari di Indonesia: Kontribusi dari Managing Identity
Yonathan Aditya, Ihan Martoyo
Veritas : Jurnal Teologi dan Pelayanan.2024; 23(1): 111. CrossRef - Impact of provoked stress on model-free and model-based reinforcement learning in individuals with alcohol use disorder
Florent Wyckmans, Armand Chatard, Charles Kornreich, Damien Gruson, Nemat Jaafari, Xavier Noël
Addictive Behaviors Reports.2024; 20: 100574. CrossRef - Factors affecting the patient safety activities of hospital nurses: A cross-sectional study focusing on shared leadership
Bokyung Kim, Soyoung Yu
Safety Science.2024; 174: 106460. CrossRef - Teacher support promotes the classroom engagement of mathematically poor students: a moderated mediation model
Peiling Zhou, Wenwen Sun, Yue Zhou, Tingting Li
Educational Psychology.2024; 44(8): 852. CrossRef - Misperception of the facial appearance that the opposite-sex desires
David I. Perrett, Iris J. Holzleitner, Xue Lei, Johannes Hönekopp
PLOS ONE.2024; 19(11): e0310835. CrossRef - Autobiographical memory of blind and sighted early teenagers: Memory accessibility, episodicity and phenomenology
Naziye Güneş‐Acar, Ali İ. Tekcan
Applied Cognitive Psychology.2024;[Epub] CrossRef - Alleviating urban poverty in India: the role of capabilities and entrepreneurship development
Jaskirat Singh, Manjit Singh
International Journal of Social Economics.2024; 51(10): 1314. CrossRef - Effects of Simulation Games on students’ Computational Thinking and Game Experience for Programming Courses in Primary School
Nikolaos Pellas
Computers in the Schools.2024; 41(1): 23. CrossRef - Parenting stress, anxiety, and sources of acquiring knowledge in Taiwanese caregivers of children with attention-deficit/hyperactivity disorder
Tai-Ling Liu, Ray C. Hsiao, Wen-Jiun Chou, Cheng-Fang Yen
BMC Public Health.2024;[Epub] CrossRef - Evaluation of a psychological readiness program and final clinical practicum among final year nursing students: A mixed methods study
Wei How Darryl ANG, Kai Chow CHOI, Ying LAU, Lubna SHAH, Jun Jie Nicholas KOH, Zheng An TOH, Chiew Jiat Rosalind SIAH, Sok Ying LIAW, Siew Tiang LAU
Nurse Education Today.2024; 141: 106317. CrossRef - Cross-cultural adaptation and validation of Diabetes Quality of Life Brief Clinical Inventory in Turkish patients with type 2 diabetes mellitus
Tülay Çevik Saldıran, İlke Kara, Erhan Dinçer, Özgül Öztürk, Rumeysa Çakıcı, Thomas Burroughs
Disability and Rehabilitation.2024; 46(5): 995. CrossRef - The Telephone Language Screener (TLS): standardization of a novel telephone-based screening test for language impairment
Edoardo Nicolò Aiello, Veronica Pucci, Lorenzo Diana, Alessia Corvaglia, Aida Niang, Silvia Mattiello, Alice Naomi Preti, Giorgia Durante, Adele Ravelli, Lucia Consonni, Carolina Guerra, Adriana Delli Ponti, Gaia Sangalli, Teresa Difonzo, Stefano Scarano,
Neurological Sciences.2024; 45(5): 1989. CrossRef - Cause – effect relationship of trust of buyer – suppliers' integration on procurement performance in large manufacturing firms in Tanzania
Honest F. Kimario, Alex R. Kira
Journal of Global Operations and Strategic Sourcing.2024; 17(4): 708. CrossRef - Cross-sectional evaluation of pharmaceutical care competences in nurse education: how well do curricula prepare students of different educational levels?
Elyne De Baetselier, Nienke E. Dijkstra, Luis M. Batalha, Paulo A. Carvalho Ferreira, Izabela Filov, Vigdis A. Grøndahl, Jana Heczkova, Ann K. Helgesen, Sue Jordan, Igor Karnjuš, Petros Kolovos, Gero Langer, Manuel Lillo-Crespo, Alba Malara, Hana Padyšako
BMC Nursing.2024;[Epub] CrossRef - Linking employee traits to supervisor-related task performance in post-pandemic era: the mediating/moderation role of career adaptability and career identity
Farhan Mirza, Naveed Iqbal Chaudhry
IIMT Journal of Management.2024;[Epub] CrossRef - Effects of Oxytocin Pathway Gene Polymorphisms and Adverse Childhood Experiences on the Recognition of Emotion in Schizophrenia Spectrum Disorders
M. V. Alfimova, V. A. Mikhailova, M. V. Gabaeva, V. V. Plakunova, T. V. Lezheiko, V. E. Golimbet
Neuroscience and Behavioral Physiology.2024; 54(2): 235. CrossRef - Examining the Intention to Adopt an Online Platform for Freight Forwarding Services in Thailand: A Modified Unified Theory for Acceptance and Use of Technology (UTAUT) Model Approach
Nattakorn Pinyanitikorn, Walailak Atthirawong, Wirachchaya Chanpuypetch
Logistics.2024; 8(3): 76. CrossRef - Olfactory training improves emotion matching ability in 6–9 years old children — preliminary evidence
Michal Pieniak, Marta Rokosz, Zorana Ivcevic, Aleksandra Reichert, Barbara Żyżelewicz, Paulina Nawrocka, Izabela Lebuda, Anna Oleszkiewicz
Journal of Sensory Studies.2024;[Epub] CrossRef - Examination of the relationship between mathematical and critical thinking skills and academic achievement
Zubeyde Er
Pedagogical Research.2024; 9(1): em0176. CrossRef - The chain mediating role of social support and positive coping between neuroticism and depressive symptoms among graduate students
Peng Wan, Jinsheng Hu, Qingshuo Yang
Frontiers in Psychiatry.2024;[Epub] CrossRef - Can host–tourist interaction pull the plug on tourist stereotypes? Exploring the power of emotional solidarity
Guoxiong Tan, Cathy H.C. Hsu
Tourism Management Perspectives.2024; 50: 101211. CrossRef - Differences in Foot Morphology across Age Groups for Women Active in Sport
Joanna Reeves, Roxana Buckley, Sharon Dixon
Gerontology.2024; 70(12): 1267. CrossRef - Indian validation of Rosenberg’s Self-Esteem Scale in Hindi among adults
Ruchi Singh, Akbar Husain
Mental Health, Religion & Culture.2024; : 1. CrossRef - Psychopathy traits explain variance shared between features of substance use disorders and violence
Samuel R. Vincent, Emily E. Graupman, William J. McGarrigle, David S. Kosson
Criminal Behaviour and Mental Health.2024; 34(5): 431. CrossRef - Self-reported sensory impairment and social participation among Korean older adults: mediating roles of cognitive function and digital technology use
Juhyeong Lee, Giyeon Kim
Aging & Mental Health.2024; 28(12): 1686. CrossRef - The Impact of Internet Addiction on Mental Health: Exploring the Mediating Effects of Positive Psychological Capital in University Students
Girum Tareke Zewude, Derib Gosim Bereded, Endris Abera, Goche Tegegne, Solomon Goraw, Tesfaye Segon
Adolescents.2024; 4(2): 200. CrossRef - The impact of knowledge incompatibility and communication style differences on patients’ perceived value of online medical consultations
Jiamin Peng, Lingwen Huang, Yujuan Guo, Xiaoyun Yang, Yue Chen
Service Business.2024; 18(3-4): 473. CrossRef - Psychological flexibility in somatic symptom and related disorders: A case control study
René J.D.M. Selker, Tim Y. Koppert, Jan H. Houtveen, Rinie Geenen
Journal of Psychiatric Research.2024; 173: 398. CrossRef - Development and Validation of the Bystander Engagement Scale for Witnessed Intimate Partner Violence: A South Korean Version
Sihyun Park, Yejung Ko
Journal of Interpersonal Violence.2024; 39(13-14): 2959. CrossRef - Attitudes of patients with schizophrenia spectrum or bipolar disorders towards medication self‐management during hospitalisation
Elke Loots, Tinne Dilles, Bart Van Rompaey, Manuel Morrens
Journal of Clinical Nursing.2024; 33(4): 1459. CrossRef - Linkage between role stress and work engagement among specialty nurses: a cross-sectional study of China
Panpan Zhang, Yaru Li, Songyao Li, Liming Li, Shuying Chang, Ziru Fang, Fangfang Liang, Hongmei Zhang
BMJ Open.2024; 14(8): e079979. CrossRef - Bilişsel, Duygusal ve Davranışsal Öz Düzenleme Performanslarının Akademik Başarıya Etkisi: İlkokul İkinci Sınıf Öğrencileri Örneği
İhsan Akeren
MANAS Sosyal Araştırmalar Dergisi.2024; 13(4): 1455. CrossRef - Determination of a cut-off COmprehensive Score for financial Toxicity (COST) for identifying cost-related treatment nonadherence and impaired health-related quality of life among Chinese patients with cancer
Binbin Xu, Winnie K. W. So, Kai Chow Choi
Supportive Care in Cancer.2024;[Epub] CrossRef - Exploring the associations between muscularity teasing and eating and body image disturbances in Chinese men and women
Jinbo He, Shuqi Cui, Tianxiang Cui, Wesley R. Barnhart, Jiayi Han, Yinuo Xu, Jason M. Nagata
Body Image.2024; 49: 101697. CrossRef - The Effects of Different Stretching Techniques Used in Warm-Up on the Triggering of Post-Activation Performance Enhancement in Soccer Players
Kemal Kurak, İsmail İlbak, Stefan Stojanović, Ramazan Bayer, Tijana Purenović-Ivanović, Tomasz Pałka, Tadeusz Ambroży, Krzysztof Kasicki, Wojciech Czarny, Łukasz Rydzik
Applied Sciences.2024; 14(11): 4347. CrossRef - Developing a scale to explore self-regulatory approaches to assessment and feedback with academics in higher education
Carol Evans, William Kay, Sheila Amici-Dargan, Rafael De Miguel González, Karl Donert, Stephen Rutherford
Frontiers in Psychology.2024;[Epub] CrossRef - Coping strategy-situation fit vs. present control: relations with perceived stress in U.S. college students
Abby I. Person, Patricia A. Frazier
Anxiety, Stress, & Coping.2024; 37(2): 219. CrossRef - Psychometric evaluation of the Indonesian version of paternal breastfeeding self-efficacy scale- short form: A confirmatory factor analysis
Mega Hasanul Huda, Yeni Rustina, Fajar Tri Waluyanti, Cindy-Lee Dennis, Shu-Yu Kuo
Midwifery.2024; 139: 104182. CrossRef - Emotional Contagion—As a Moderator in Personality and Organizational Citizenship Behavior Relationship
Elavarasi G. N. Anitha, L. Suganthi, J. Irudhaya Rajesh, G. N. Sumathi
Business Perspectives and Research.2024; 12(2): 277. CrossRef - Açık ve uzaktan öğrenmede öğrenenlerin sosyal bulunuşluk düzeylerinin, etkileşim örüntülerinin ve öğrenme malzemeleri tercihlerinin incelenmesi
Mesut Aydemir
Nevşehir Hacı Bektaş Veli Üniversitesi SBE Dergisi.2024; 14(3): 1322. CrossRef - 3-5 Yaş çocukları için empati ve zihin kuramı ölçeği Türkçe geçerlik-güvenirlik çalışması ve bazı değişkenler açısından incelenmesi
Canan Keleş Ertürk, Kezban Tepeli
Çocuk ve Gelişim Dergisi.2024; 7(13): 13. CrossRef - Verbal and non-verbal recognition memory assessment: validation of a computerized version of the Recognition Memory Test
Elena Baruzzo, Stefano Terruzzi, Beatrice Feder, Costanza Papagno, Daniela Smirni
Neurological Sciences.2024; 45(5): 1979. CrossRef - Emotional Wellbeing of Asylum-Seeking Children After Release From Immigration Detention
Luis H. Zayas, Alice P. Villatoro, Tatiana Londoño, Jaime Fuentes-Balderrama
Hispanic Journal of Behavioral Sciences.2024; 46(4): 206. CrossRef - Empowering Through Sports: Breaking the Cycle of Adverse Childhood Experiences and Aggressive Behavior
Joyce Hoeven, Stefan Bogaerts, Marija Janković
Journal of Aggression, Maltreatment & Trauma.2024; 33(9): 1154. CrossRef - Mediating Role of Financial Toxicity in the Relationships Between Health-Related Quality of Life and Its Risk Factors in Chinese Patients With Cancer
Binbin Xu, Winnie K. W. So, Kai Chow Choi, Yu Huang, Mei Liu, Lanxiang Qiu, Jianghong Tan, Hua Tao, Keli Yan, Fei Yang
Cancer Nursing.2024;[Epub] CrossRef - ÖZEL EĞİTİM BÖLÜMÜ ÖĞRENCİLERİNİN DOĞAL AFET OKURYAZARLIK DÜZEYLERİNİN ÇEŞİTLİ DEĞİŞKENLER AÇISINDAN İNCELENMESİ
Fatma Yıldırım
Mehmet Akif Ersoy Üniversitesi Eğitim Fakültesi Dergisi.2024; (70): 144. CrossRef - Reducing alcohol and cannabis use risk in South American young adults: is behavioral economics an effective approach? Results from a randomized controlled pilot trial
Angela J. Pereira-Morales, Felipe Ramírez Cortázar, María Fernanda Redondo Mayorga, Javier Hernando Eslava-Schmalbach
Current Psychology.2024; 43(44): 34254. CrossRef - Environmental Implications of Using Waste Glass as Aggregate in Concrete
Robert Lopez, Charbel El-Fata
Journal of Composites Science.2024; 8(12): 507. CrossRef - Validity and Reliability of the Korean Version of Reduced Morningness–Eveningness Questionnaire: Results From a General Population-Based Sample
Heewon Hwang, Taesic Lee, Wonwoo Lee, Kyung Min Kim, Kyoung Heo, Min Kyung Chu
Journal of Korean Medical Science.2024;[Epub] CrossRef - Emotional labor, fatigue, and presenteeism in Chinese nurses: the role of organizational identification
Zheng Ren, Chao Zhou, Xiumin Zhang, Aoqi Yang, Wenjun Li, Hongjian Liu
BMC Nursing.2024;[Epub] CrossRef - Overparenting in Parents of Elementary School Children: The Direct Association with Positive Parent-Child Relationship and the Indirect Associations with Parental Self-Efficacy and Psychological Well-Being
Yosi Yaffe, Yael Grinshtain, Gal Harpaz
Journal of Child and Family Studies.2024; 33(3): 863. CrossRef - Motor impulsivity and problematic online behaviours among university students: the potential mediating role of coping style
Magdalena Sánchez-Fernández, Mercedes Borda-Mas
Current Psychology.2024; 43(21): 19386. CrossRef - The “thinking system” in a new school concept: A rhythmic teaching approach in physical education to develop creativity
Marta Rigon, Pietro Luigi Invernizzi, Gabriele Signorini, Athos Trecroci, Raffaele Scurati, Damiano Formenti, Dario Colella, Andrea Bosio, Domenico Cherubini, Hesam Ramezanzade
PLOS ONE.2024; 19(4): e0301858. CrossRef - Attitudes and awareness in autonomous decision on medical treatment or inclusion in clinical trials amongst Slovenian adolescents: an online survey
Maks Lenart Černelč, Vanja Erčulj, Štefan Grosek
BMC Medical Education.2024;[Epub] CrossRef - Sensing the body matters: profiles of interoceptive sensibility in chronic pain adjustment
Inês Oliveira, Margarida Vaz Garrido, Helena Carvalho, Sónia Figueira Bernardes
Pain.2024; 165(2): 412. CrossRef - The Problematic Online Dating Apps Use Scale (PODAUS): Development and evaluation of its psychometric properties
Alessio Gori, Eleonora Topino, Mark D. Griffiths
Addictive Behaviors Reports.2024; 19: 100533. CrossRef - Group dance, social cohesion, and social identity in the Yali society from Papua
Piotr Sorokowski, Jerzy Luty, Wojciech Malecki, Marta Kowal
Musicae Scientiae.2024; 28(2): 388. CrossRef - Roles of stakeholders for adopting sustainable design in buildings
Nor Aqilah Haji Juffle, Md Motiar Rahman, Rajul Adli Asli
Building Engineering.2024; 2(1): 561. CrossRef - Psychological resilience and hardiness as protective factors in the relationship between depression/anxiety and well-being: Exploratory and confirmatory evidence
Anne E. Chuning, Michelle R. Durham, William D.S. Killgore, Ryan Smith
Personality and Individual Differences.2024; 225: 112664. CrossRef - Validation of the Short Version (TLS-15) of the Triangular Love Scale (TLS-45) across 37 Languages
Marta Kowal, Piotr Sorokowski, Bojana M. Dinić, Katarzyna Pisanski, Biljana Gjoneska, David A. Frederick, Gerit Pfuhl, Taciano L. Milfont, Adam Bode, Leonardo Aguilar, Felipe E. García, S. Craig Roberts, Beatriz Abad-Villaverde, Tina Kavčič, Kirill G. Mir
Archives of Sexual Behavior.2024; 53(2): 839. CrossRef - Portfolyoya Dayalı Durum Belirlemenin Öğrencilerin Dinlemeye Yönelik Üstbilişsel Farkındalık, Motivasyon ve Başarısına Etkisi
Mustafa Aydın, Özen Yıldırım
Ana Dili Eğitimi Dergisi.2024; 12(4): 746. CrossRef - Maternal and Child Depressive Symptoms in a Sample of Low-income Families of Color: The Mediating Role of Child Adaptability
Kevin M. Wagner, Delida Sanchez, Carmen R. Valdez
Child Psychiatry & Human Development.2024; 55(1): 287. CrossRef - Using Evolutionary Theory to Understand Associations Between Passive and Active Social Media Use and Well-Being
Aris Karagiorgakis, Kaylee Aaron
The American Journal of Psychology.2024; 137(1): 39. CrossRef - Can’t stop, won’t stop - understanding anxiety’s role in cyberchondria among pregnant women
Matea Šoštarić, Nataša Jokić-Begić, Matea Vukušić Mijačika
Women & Health.2024; 64(2): 185. CrossRef - Residents' Support for Major Sporting Events in the Postponement Context: A Case Study of the 31st Summer Universiade
Wenxuan Gan, Qiang Dong
International Journal of Tourism Research.2024;[Epub] CrossRef - Türkiye ve KKTC'de Çalışan Hemşirelerin Palyatif Bakım Bilgi Düzeylerinin Karşılaştırılması ve Etkileyen Faktörlerin İncelenmesi
Çiğdem Müge Haylı, Dilek Demir, Neşe Ataman Bor, Rasiha Güler
Sağlık Akademisi Kastamonu.2024; 9(2): 241. CrossRef - Public Harassment of Runners in the United States: Differences by Gender and Sexual Orientation
Cassandra N. Davis, Kayla A. Huber, Patricia A. Frazier
Psychology of Women Quarterly.2024; 48(3): 359. CrossRef - Noise sensitivity or hyperacusis? Comparing the Weinstein and Khalfa questionnaires in a community and a clinical samples
Charlotte Bigras, Sarah M. Theodoroff, Emily J. Thielman, Sylvie Hébert
Hearing Research.2024; 445: 108992. CrossRef - Assessing alexithymia in adolescents: psychometric properties of the Perth Alexithymia Questionnaire in high school students
Annette C. Trimble, Ken Robinson, David A. Preece
Australian Psychologist.2024; 59(5): 422. CrossRef - A model for assessing student satisfaction with smart classroom environment in higher education
Zhicheng Dai, Ling Wang, Xian Peng, Liang Zhao, Junxia Xiong
Journal of Computer Assisted Learning.2024; 40(6): 2901. CrossRef - The relationship between spiritual health and COVID-19 anxiety among nurses: a national online cross-sectional study
Arezoo Davarinia Motlagh Quchan, Fatemeh Mohammadzadeh, Zohreh Mohamadzadeh Tabrizi, Narjes Bahri
Scientific Reports.2024;[Epub] CrossRef - Mitigating destructive deviance in organisations: assessing the role of perceived HRM practices and perceived organisational support
Pooja Malik, Parul Malik
International Journal of Organizational Analysis.2024; 32(7): 1242. CrossRef - Is Immersion in 3D Virtual Games Associated with Mathematical Ability Improvement in Game-Based Learning?
Athanasios Christopoulos, Stylianos Mystakidis, Justyna Kurczaba, Mikko-Jussi Laakso, Chrysostomos Stylios
International Journal of Science and Mathematics Education.2024; 22(7): 1479. CrossRef - Impact of type and position of abutment connection on microstrain distribution: an in vitro study
Jekita Siripru, Usanee Puengpaiboon, Chamaiporn Sukjamsri, Basel Mahardawi, Napapa Aimjirakul
The Journal of Advanced Prosthodontics.2024; 16(5): 290. CrossRef - Invarianza de la Escala de Evaluación de las Relaciones Intrafamiliares en padres con y sin migración de retorno y salud mental
María Elena Rivera-Heredia, Patricia Andrade-Palos, Jaime Fuentes-Balderrama, Luis H. Zayas
Enseñanza e Investigación en Psicología Nueva Época.2024; 6(Migracione): 42. CrossRef - Positive Youth Development Program for Adolescents with Disabilities: A Pragmatic Trial
Daniel Page, Stephanie Hanrahan, Lisa Buckley
International Journal of Disability, Development and Education.2024; 71(3): 451. CrossRef - Psychometrics and diagnostics of the Italian version of the Alternate Verbal Fluency Battery (AVFB) in non-demented Parkinson’s disease patients
Edoardo Nicolò Aiello, Francesca Mameli, Fabiana Ruggiero, Eleonora Zirone, Stefano Zago, Sylvie Piacentini, Barbara Poletti, Maria Rita Reitano, Gabriella Santangelo, Nicola Ticozzi, Vincenzo Silani, Alberto Priori, Roberta Ferrucci
Neurological Sciences.2024; 45(8): 3767. CrossRef - Virtual Reality for Subacute Pain After Orthopedic Traumatic Musculoskeletal Injuries
Ryan A. Mace, Julie R. Brewer, Joshua E. Cohen, Thuan V. Ly, Michael J. Weaver, David Borsook
The Clinical Journal of Pain.2024; 40(9): 526. CrossRef - Mindfulness, mental health, and motives for eating tasty foods when not in metabolic need
Katherine G. Moore, Justess D. Rice, John E. Gampher, Mary M. Boggiano
Frontiers in Psychology.2024;[Epub] CrossRef - Tour guides’ interpretation and tourists’ pro-environmental behavior: differences across cultural and natural world heritage sites
Yahya A. Alzghoul, Malek M. Jamaliah, Mohammad M. Alazaizeh, John T. Mgonja, Zaha J. Al-Daoud
Journal of Ecotourism.2024; 23(3): 366. CrossRef - Assessing the Impact of COVID-19 on Capital Structure Dynamics: Evidence from GCC Economies
Amanj Mohamed Ahmed, Deni Pandu Nugraha, István Hágen
Economies.2024; 12(5): 103. CrossRef - Effects of the eccentric chin closure exercise on submental muscle activation, muscle strength, dysphagia limit, perceived exertion and pain in healthy volunteers: A prospective, randomized parallel group study
Emre Cengiz, Selen Serel Arslan, Ömer Faruk Yaşaroğlu, Rabia Alıcı, Numan Demir, Mehmet Akif Topçuoğlu, Akmer Mutlu, Masatoshi Nakamura
PLOS ONE.2024; 19(11): e0313995. CrossRef - Attachment style to body dissatisfaction, restrained eating, and disordered eating in adolescent girls: Differential weight communication mediators
Valerie Valledor, Jamie Lawler, Stephen Jefferson, Chong Man Chow
Appetite.2024; 198: 107321. CrossRef - Role of Algorithm Awareness in Privacy Decision-Making Process: A Dual Calculus Lens
Sujun Tian, Bin Zhang, Hongyang He
Journal of Theoretical and Applied Electronic Commerce Research.2024; 19(2): 899. CrossRef - Integration of epidemiological and blood biomarker analysis links haem iron intake to increased type 2 diabetes risk
Fenglei Wang, Andrea J. Glenn, Anne-Julie Tessier, Zhendong Mei, Danielle E. Haslam, Marta Guasch-Ferré, Deirdre K. Tobias, A. Heather Eliassen, JoAnn E. Manson, Clary Clish, Kyu Ha Lee, Eric B. Rimm, Dong D. Wang, Qi Sun, Liming Liang, Walter C. Willett,
Nature Metabolism.2024; 6(9): 1807. CrossRef - Investigating metaemotions as the predictors of willingness to communicate, anxiety, and enjoyment among EFL learners
Nourollah Zarrinabadi, Marzieh Mehri, Behrouz Jamalvandi
Journal of Multilingual and Multicultural Development.2024; : 1. CrossRef - Health behavior and psychological treatment utilization in adults with avoidant/restrictive food intake disorder symptoms
Julia Enya Engelkamp, Andrea Sabrina Hartmann, Katja Petrowski, Benedict Herhaus, Jörg Michael Fegert, Cedric Sachser, Peter Kropp, Britta Müller, Elmar Brähler, Anja Hilbert
Journal of Eating Disorders.2024;[Epub] CrossRef - Towards improving online learning in physical education: Gender differences and determinants of motivation, psychological needs satisfaction, and academic achievement in Saudi students
Mohamed Frikha, Nourhen Mezghanni, Nesrine Chaâri, Noureddine Ben Said, Mohammed S. Alibrahim, Majed M. Alhumaid, Marwa M. Hassan, Raghad S. Alharbi, Mostafa S. Amira, Nasser Abouzeid, Chao Gu
PLOS ONE.2024; 19(2): e0297822. CrossRef - Initial Development of a Second Language Discussion Task-Specific Self-Efficacy Instrument: An Illustration for Frontline Researchers
Joseph P Vitta, Paul Leeming, Stuart McLean, Christopher Nicklin
RELC Journal.2024; 55(3): 764. CrossRef - Neuropsychiatric symptoms and metamemory across the life span: psychometric properties of the German Multifactorial Memory Questionnaire (MMQ)
Sophia Rekers, Josephine Heine, Angelika I. T. Thöne-Otto, Carsten Finke
Journal of Neurology.2024; 271(7): 4551. CrossRef - Finer aspects of spatio-temporal variations in Indian summer monsoon rainfall trend reversals over the last 120 years
Swagatika Chakra, Harsh Oza, Akash Ganguly, Amit Pandey, Virendra Padhya, R. D. Deshpande
Climatic Change.2024;[Epub] CrossRef - An out-of-sample perspective on the assessment of incremental predictive validity
Bunga Citra Pratiwi, Elise Dusseldorp, Mark de Rooij
Behaviormetrika.2024; 51(2): 539. CrossRef - Precisely identifying and mitigating shallow reading behaviors through online reading data: exploring quantitative reading behavior methods and precise behavioral intervention
Yu Bai, Fuzheng Zhao, Etsuko Kumamoto, Chengjiu Yin
Interactive Learning Environments.2024; : 1. CrossRef - Need to Belong and Cognitive Flexibility in Young Adults: Mediating Role of Negative Affect and Moderating Role of Agreeableness
Selin Yılmaz, Rana Alan
Psikiyatride Güncel Yaklaşımlar.2024; 16(Supplement): 79. CrossRef - Unravelling the interplay between competencies, career preparedness, and perceived employability among postgraduate students: a structural model analysis
Ranjit I George, Bino Paul
Asia Pacific Education Review.2024; 25(2): 439. CrossRef - Financial toxicity and its risk factors among patients with cancer in China: A nationwide multisite study
Binbin Xu, Winnie K.W. So, Kai Chow Choi, Yu Huang, Mei Liu, Lanxiang Qiu, Jianghong Tan, Hua Tao, Keli Yan, Fei Yang
Asia-Pacific Journal of Oncology Nursing.2024; 11(5): 100443. CrossRef - Determinants of source waste separation behavior in Iranian high school students: An application of the theory of planned behavior
Zhila Alimardani, Khadijeh Hajimiri, Fatemeh Jafari, Gholamreza Sadeghi
Environmental Health Engineering and Management.2024; 11(3): 293. CrossRef - Nocturnal pulse oximetry for the detection and prediction of acute mountain sickness: An observational study
Kelsey E. Joyce, Kimberly Ashdown, John P. Delamere, Chris Bradley, Christopher T. Lewis, Abigail Letchford, Rebekah A. I. Lucas, Will Malein, Owen Thomas, Arthur R. Bradwell, Samuel J. E. Lucas
Experimental Physiology.2024; 109(11): 1856. CrossRef - Validation of the Good Lives Assessment of Domains in an Adult U.S. Sample
Jeremy Olson, Dennis Giever, Rebecca S. Sarver
International Journal of Offender Therapy and Comparative Criminology.2024;[Epub] CrossRef - Internalized Stigma and its Correlates Among Opioid Agonist Treatment Service Users in Nepal
Sagun Ballav Pant, Suraj Bahadur Thapa, John Howard, Saroj Prasad Ojha, Lars Lien
Journal of Psychosocial Rehabilitation and Mental Health.2024; 11(3): 361. CrossRef - Service Quality of Amman BRT Based on User's Perceptions: A Structural Equation Modeling Approach
Esra'a Al-haj, Shrooq Alamoush, Motasem M. Darwish
KSCE Journal of Civil Engineering.2024; 28(8): 3506. CrossRef - Symbolically Simple: How Simple Packaging Design Influences Willingness to Pay for Consumable Products
Lan Anh N. Ton, Rosanna K. Smith, Julio Sevilla
Journal of Marketing.2024; 88(2): 121. CrossRef - Green Consumer Profiling and Online Shopping of Imperfect Foods: Extending UTAUT with Web-Based Label Quality for Misshapen Organic Produce
Rara Dwi Oktaviani, Phaninee Naruetharadhol, Siraphat Padthar, Chavis Ketkaew
Foods.2024; 13(9): 1401. CrossRef - Factors associated with depression, anxiety, and satisfaction with life among Malaysian parental caregivers of adolescent psychiatric patients: A cross-sectional study
Choy Qing Cham, Norhayati Ibrahim, Clarisse Roswini Kalaman, Meng Chuan Ho, Uma Visvalingam, Farah Ahmad Shahabuddin, Fairuz Nazri Abd Rahman, Mohd Radzi Tarmizi A. Halim, Manveen Kaur Harbajan Singh, Fatin Liyana Azhar, Amira Najiha Yahya, Samsilah Rosla
Cambridge Prisms: Global Mental Health.2024;[Epub] CrossRef - Investigating knowledge of DRLs, image quality and radiation dose in PET/CT and CT imaging among medical imaging professionals
Qays Alhorani, Akram Al-Ibraheem, Mohammad Rawashdeh, Essam Alkhybari, Akmal Sabarudin, Rukiah A. Latiff, Mazlyfarina Mohamad
Heliyon.2024; 10(9): e30030. CrossRef - Defensive pessimism and its effect on supply chain performance
Uchenna Peter Ekezie, Seock-Jin Hong
The International Journal of Logistics Management.2024; 35(1): 56. CrossRef - Radon (Rn-222) activity measurement in ground water and associated dose estimation in Raghunathpur and Jhalda municipalities of Purulia district, West Bengal, India
Joydeep Mukherjee, Sayantan Mitra, Sushanta Sutradhar, Sonjoy Mondal, Chiranjib Barman
Journal of Radioanalytical and Nuclear Chemistry.2024; 333(3): 1427. CrossRef - Does emotional eating status affect food addiction of paramedics? A cross-sectional study
İrem Nur Akdeniz, Hasan Kaan Kavsara, Pınar Usta, Irem Kaya Cebioglu
Nutrition & Food Science .2024; 54(3): 637. CrossRef - How adolescents’ perceived teachers’ mindset beliefs influence school engagement in China: Roles of perceived classroom goal structures and adolescents’ mindset beliefs
Xiaoyu Jia, Ping Li, Jing Zhao, Yuchi Zhang
School Psychology International.2024; 45(5): 465. CrossRef - Application of fuzzy Delphi technique to identify analytical lenses for determining the preparation of free and open source software projects for user experience maturity
Phesto P. Namayala, Tabu S. Kondo
Science of Computer Programming.2024; 237: 103136. CrossRef - Organizational Diversity and Inclusion Scale (ODIS): A multilevel approach
Silvia De Simone, Pietro Menatta, Laura Borgogni
European Review of Applied Psychology.2024; 74(5): 101009. CrossRef - Inflammatory bowel disease patients’ perspectives of non-medical needs
Narges Norouzkhani, Mahbobeh Faramarzi, Ali Bahari, Javad Shokri Shirvani, Saeid Eslami, Hamed Tabesh
BMC Gastroenterology.2024;[Epub] CrossRef - Association Between Self-Construals, Social Pain Sensitivity, and Gender in Young Adults
Masataka Umeda, Se-Woong Park
The Journal of Psychology.2024; 158(8): 650. CrossRef - The Dark Triad and aggression among drug abstainers: a moderated mediation model of self-control and physical exercise
Li-Shuang Chen, Ying Yao, Ming-Sheng Xiong
BMC Psychiatry.2024;[Epub] CrossRef - The protective role of valuing cultural activities on cannabis use in reserve-Dwelling First Nation youth
Rachel Girard, Tessa Nalven, Nichea S. Spillane
Journal of Ethnicity in Substance Abuse.2024; : 1. CrossRef - Dynamic interplays between self-regulated learning and computational thinking in primary school students through animations and worksheets
Siu-Cheung Kong, Yi-Qing Wang
Computers & Education.2024; 220: 105126. CrossRef - Investigation of Candidate Teachers' Early Teacher Identity with Public Personnel Selection Examination Anxiety Levels
Selim Asan, Edanur Yağan
Journal of Computer and Education Research.2024; 12(24): 568. CrossRef - The Portuguese version of the societal attitudes towards autism (SATA) scale: Psychometric properties, confirmatory factor analysis and reliability
Hugo Fonseca, Andreia A. Manão, Laura Lemos, Marina Cunha, Diogo Carreiras
British Journal of Special Education.2024; 51(3): 369. CrossRef - Development and validation of a patient‐reported outcome measure for hair loss treatment: The HAIR‐Q
Anne F. Klassen, Jasmine Mansouri, Manraj Kaur, Charlene Rae, Lotte Poulsen, Steven Dayan, Stefan J. Cano, Andrea L. Pusic
Journal of Cosmetic Dermatology.2024; 23(11): 3705. CrossRef - Longitudinal Associations Between Competition Contingent Self-Worth and Materialistic Values Among Chinese College Students: A Latent Growth Model
Cong Yi, Jun Wei, Yanyan Liu, Minglu Zheng
Emerging Adulthood.2024; 12(5): 781. CrossRef - Medication Literacy and Medication Self‐Management: A Cross‐Sectional Study in Hospitalised Patients (65+) With Polypharmacy
Laura Mortelmans, Jenny Gentizon, Tinne Dilles, Malakeh Malak
Journal of Nursing Management.2024;[Epub] CrossRef - Development and validation of a questionnaire about reasons for academic cheating by nursing students: A cross-sectional study
Jazi Shaydied Alotaibi, Abdullah Obaid Alotaibi, Md Dilshad Manzar, Ahmed Mansour Almansour, Sharifa Alasiry, Bader A. Alrasheadi, Wdad Alanazy, Abdulrhman Albougami, Faizan Zaffar Kashoo
Medicine.2024; 103(23): e38243. CrossRef - Inclusive attitudes: typically developing students and students with disabilities in UAE classrooms
Samir Dukmak, Eid G. Abo Hamza, Razan Alkhatib, Wid Daghustani, Dalia Bedewy
Frontiers in Education.2024;[Epub] CrossRef - Aggression in online gaming: the role of online disinhibition, social dominance orientation, moral disengagement and gender traits among Chinese university students
Wenxuan Gan, Zichao Chen, Zhusheng Wu, Xia Huang, Fang Wang
Frontiers in Public Health.2024;[Epub] CrossRef - Acute Effects of Kickboxing K1 Matches on Hematological Parameters of Kickboxers
Marta Niewczas, İsmail İlbak, Serkan Düz, Tomasz Pałka, Tadeusz Ambroży, Henryk Duda, Wojciech Wąsacz, Paweł Król, Robert Czaja, Łukasz Rydzik
Journal of Functional Morphology and Kinesiology.2024; 9(3): 130. CrossRef - How travel vlog audience members become tourists: Exploring audience involvement and travel intention
Jiajing Hu, Hua Wang, Liangqiang Li, Ling Guo
Computers in Human Behavior.2024; 152: 108045. CrossRef - Characteristic and allowable compressive strengths of Dendrocalamus Sericeus bamboo culms with/without node using artificial neural networks
Chinnapat Buachart, Chayanon Hansapinyo, Piti Sukontasukkul, Hexin Zhang, Worathep Sae-Long, Panatchai Chetchotisak, Timothy E. O'Brien
Case Studies in Construction Materials.2024; 20: e02794. CrossRef - Functional Characteristics and Coping Strategies among Rugby Athletes: A Cluster Analysis Approach
Walter Sapuppo, Davide Giacconi, Vincenzo Monda, Antonietta Messina, Salvatore Allocca, Sergio Chieffi, Mariateresa Ricci, Ines Villano, Daniele Saccenti, Claudia Maria Mineo, Margherita Boltri, Marcellino Monda, Girolamo Di Maio, Antonietta Monda, Marco
Journal of Personalized Medicine.2024; 14(3): 292. CrossRef - Exploring the efficacy of collaborative learning in a remote robotics laboratory: a comparative analysis of performance and pedagogical approaches
Long Teng, Yuk Ming Tang, Raymond P. H. Wu, Gary C. P. Tsui, Yung Po Tsang, Chak Yin Tang
Smart Learning Environments.2024;[Epub] CrossRef - Individual and Organizational Ductility: Conceptualization, Development, and Validation of a New Scale
Flavio Urbini, Emanuela Caracuzzo, Antonio Chirumbolo, Antonino Callea
Behavioral Sciences.2024; 14(6): 511. CrossRef - The differential effect of psychopathy on active and bystander trolling behaviors: the role of dark tetrad traits and lower agreeableness
Anantha Ubaradka, Sanjram Premjit Khanganba
Scientific Reports.2024;[Epub] CrossRef - The Effects of Childhood Adversity and Self-Regulation on the Well-Being of Adults with Delinquency Histories: A Mediation Model
Michelle-Ann Rhoden-Neita, Hui Huang, Nicole M. Fava
Journal of Evidence-Based Social Work.2024; 21(1): 117. CrossRef - The Relationship among Internet Addiction, Moral Potency, Mindfulness, and Psychological Capital
Girum Tareke Zewude, Tun Zaw Oo, Gabriella Józsa, Krisztián Józsa
European Journal of Investigation in Health, Psychology and Education.2024; 14(6): 1735. CrossRef - A study of the relationship between leisure-time physical activity and residents’ quality of life
Chengkai Feng, Zhenguo Shi, Yuge Tian, Chao Ma, Jianmin Liu
Current Psychology.2024; 43(26): 22259. CrossRef - Positive and negative emotions, L2 grit and perceived competence as predictors of L2 motivated behaviour
Mirosław Pawlak, Nourollah Zarrinabadi, Mariusz Kruk
Journal of Multilingual and Multicultural Development.2024; 45(8): 3188. CrossRef - Children and adolescents with primary headaches exhibit altered sensory profiles – a multi-modal investigation
Michal Pieniak, Berit Höfer, Jenny Knipping, Vanda Faria, Matthias Richter, Valentin A. Schriever, Antje Haehner, Gudrun Gossrau
The Journal of Headache and Pain.2024;[Epub] CrossRef - Combining the Nurse Intuition Patient Deterioration Scale with the National Early Warning Score provides more Net Benefit in predicting serious adverse events: A prospective cohort study in medical, surgical, and geriatric wards
Filip Haegdorens, Julie Lefebvre, Carolien Wils, Erik Franck, Peter Van Bogaert
Intensive and Critical Care Nursing.2024; 83: 103628. CrossRef - The speaking proficiency outcomes of face‐to‐face and online intensive summer LCTL programs
Dianna Murphy, Sonya K. Sedivy
Foreign Language Annals.2024; 57(4): 872. CrossRef - Cultural translation of the ethical dimension: a study on the reliability and validity of the Chinese nurses’ professional ethical dilemma scale
Wei Hu, Ke Shang, Xin Wang, Xia Li
BMC Nursing.2024;[Epub] CrossRef - Adaptive Functioning in College Students Following Childhood Maltreatment
Addie N. Merians, Patricia Frazier
Adversity and Resilience Science.2024; 5(3): 283. CrossRef - Investigation on the tensile strength of Dendrocalamus sericeus, Phyllostachys makinoi, and Thyrsostachys oliveri bamboo: Experiment and simulations
Worathep Sae-Long, Thanakorn Chompoorat, Suchart Limkatanyu, Chayanon Hansapinyo, Apichat Buakla, Piti Sukontasukkul, Pannipa Chaowana, Kitti Chaowana, Tanan Chub-Uppakarn
Case Studies in Construction Materials.2024; 20: e03205. CrossRef - Validity, diagnostics and feasibility of the Italian version of the Montreal Cognitive Assessment (MoCA) in Huntington’s disease
Edoardo Nicolò Aiello, Federica Solca, Silvia Torre, Annalisa Lafronza, Alessio Maranzano, Ruggero Bonetti, Francesco Scheveger, Sabrina Maffi, Consuelo Ceccarelli, Marta Scocchia, Melissa Casella, Federico Verde, Simone Migliore, Vincenzo Silani, Nicola
Neurological Sciences.2024; 45(3): 1079. CrossRef - Histogram-Based Edge Detection for River Coastline Mapping Using UAV-Acquired RGB Imagery
Grzegorz Walusiak, Matylda Witek, Tomasz Niedzielski
Remote Sensing.2024; 16(14): 2565. CrossRef - Relationship between depression, anxiety, stress, and health-related quality of life in adults with and without chronic diseases: A cross-sectional study
Younghui Hwang, Jihyun Oh
Medicine.2024; 103(2): e36967. CrossRef - Does childhood maltreatment make us more morally disengaged? The indirect effect of expressive suppression
Alexandra Maftei, Ștefania Nițu
Ethics & Behavior.2024; 34(2): 104. CrossRef - Beyond Age, BMI, Gender Identity, and Gender Minority Stress, Weight Bias Internalization Is Uniquely Associated With More Eating and Body Image Disturbances and Poor Physical and Mental Health in Chinese Gender‐Diverse Adults
Wesley R. Barnhart, Yueyang Xiao, Yijing Li, Christina Gaggiano, Zexuan Jiang, Shijia Wu, Hongjian Cao, Jinbo He
International Journal of Eating Disorders.2024; 57(11): 2246. CrossRef - Enhancing institutional integration and enjoyment among Saudi female physical education students: exploring the mediation of motivation and psychological needs satisfaction
Mohamed Frikha, Nesrine Chaâri, Nourhen Mezghanni, Ahmad K. Hassan, Majed M. Alhumaid, Mohammed S. Alibrahim
Frontiers in Education.2024;[Epub] CrossRef - Looks, personality, and everything in between: Understanding sexually attractive characteristics among cisgender and gender diverse individuals
Rebecca Star, Maeve Mulroy, Kate Hunker, Lizeth Martínez, Caroline Pukall
The Canadian Journal of Human Sexuality.2024; 33(3): 402. CrossRef - How does interpretive tour guiding promote tourists’ pro-environmental behaviour? Evidence from Tanzania
Malek M. Jamaliah, John T. Mgonja, Mohammad M. Alazaizeh, Robert B. Powell
Tourism Recreation Research.2024; 49(2): 329. CrossRef - Stochastic neuro-fuzzy system implemented in memristor crossbar arrays
Tuo Shi, Hui Zhang, Shiyu Cui, Jinchang Liu, Zixi Gu, Zhanfeng Wang, Xiaobing Yan, Qi Liu
Science Advances.2024;[Epub] CrossRef - Towards sustainable precipitation management in Madurai Town Planning Area (India)
S. R. Thiruchelve, S. Chandran, M. Irannezhad, A. Anandhi, Kumar Veluswamy, U. Surendran
Discover Sustainability.2024;[Epub] CrossRef - Development and Psychometric Evaluation of the End-of-Life Nursing Competency Scale for Clinical Nurses
Ji-yeon Kim, Hyun-sun Kim, Mi-jung Kang, Hee-young Oh, Mi-rae Jo
Healthcare.2024; 12(16): 1580. CrossRef - Determining the Interaction of Social Sustainability with the Physical Environment: A Case Study of Adana, Turkey
Buse Acik Etike, Muyesser Ebru Erdonmez Dincer
Sustainability.2024; 16(12): 4947. CrossRef - Winter walking – the effect of winter conditions on pedestrians’ step length and step frequency
Magne Fossum, Helge Hillnhütter, Eirin Olaussen Ryeng
Transportmetrica A: Transport Science.2024;[Epub] CrossRef - Understanding the impact of human capital on radical and incremental innovation: the role of entrepreneurial passion and alertness
Tayyaba Rafique, Muhammad Mohsin, Muhammad Adeel Abid, Ali Noman Ashrif, Saliah Anwar
Future Business Journal.2024;[Epub] CrossRef - Flourishing in Education: Psychometric Properties of the Flourishing Scale in a Sample of Romanian Teachers
Beatrice Adriana Balgiu, Andrei Simionescu-Panait
Behavioral Sciences.2024; 14(5): 366. CrossRef - Interactive digital media assignments: effects on EFL learners’ overall and micro-level oral language skills
Marwa F. Hafour
Computer Assisted Language Learning.2024; 37(4): 986. CrossRef - From ocean to emotion: a pilot study exploring acute mood effects following consumption of a DHA-rich powder compared with placebo in middle-aged Australian men
Jeffery M. Reddan, Sarah Gauci, Lauren M. Young, Greg Kennedy, Renee Rowsell, Anne Marie Minihane, Andrew Scholey, Andrew Pipingas
British Journal of Nutrition.2024; : 1. CrossRef - Body Composition and Cardiorespiratory Fitness Characteristics Among Female University Students: A Cross-Sectional Study
Mădălina-Gabriela Coman, Andreea Maria Adam, Carmen Gheorghe, Mircea Dan Mocanu, Leonard Stoica, Daniel-Andrei Iordan, Ilie Onu, Dragoș Florin Teodor
Balneo and PRM Research Journal.2024; 15(Vol.15, no): 753. CrossRef - Investigating chatbot users’ e-satisfaction and patronage intention through social presence and flow: Indian online travel agencies (OTAs)
Nisha Pradeepa S.P., Asokk D., Prasanna S., Ansari Sarwar Alam
Journal of Systems and Information Technology.2024; 26(1): 89. CrossRef - Atlas of surface currents in the Mediterranean and Canary–Iberian–Biscay waters
Justino Martínez, Emilio García-Ladona, Joaquim Ballabrera-Poy, Jordi Isern-Fontanet, Sergio González-Motos, José Manuel Allegue, Cristina González-Haro
Journal of Operational Oceanography.2024; 17(1): 40. CrossRef - Complete denture palatal rugae design impact on satisfaction and quality of life
Motasum Abu‐Awwad, Mohammad Bustani, Mohammad Alkababji, Farah Majdalawi, Nesreen A. Salim, Mahmoud K. AL‐Omiri
Gerodontology.2024; 41(4): 509. CrossRef - Effects of Virtual Reality Motor-Cognitive Training for Older People With Cognitive Frailty: Multicentered Randomized Controlled Trial
Rick Yiu Cho Kwan, Justina Liu, Olive Suk Kan Sin, Kenneth N K Fong, Jing Qin, Joe Chi Yin Wong, Claudia Lai
Journal of Medical Internet Research.2024; 26: e57809. CrossRef - “The Belief to Aspire”: The Association Between Afrocentric Values in the Educational and Career Aspirations of Young Black Males
Husain Lateef, Adrian Gale, Francine Jellesma, Ellie Borgstrom
The Urban Review.2024; 56(1): 19. CrossRef - Internet addiction and psychological distress: Can social networking site addiction affect body uneasiness across gender? A mediation model
Rossella Bottaro, Giusy Danila Valenti, Palmira Faraci
Europe’s Journal of Psychology.2024; 20(1): 41. CrossRef - Investigation of readymade garment fit issues and analysis of anthropometric measurements of Ethiopian young men
Berihun Bizuneh, Abrham Destaw, Fasika Hailu, Solomon Tsegaye
Ergonomics.2024; 67(12): 1811. CrossRef - Examining the swelling potential of cohesive soils with high plasticity according to their index properties using GIS
Murat Kalkan
Open Geosciences.2024;[Epub] CrossRef - Psychological Distress and Online Academic Difficulties: Development and Validation of Scale to Measure Students’ Mental Health Problems in Online Learning
Mihai Curelaru, Versavia Curelaru
Behavioral Sciences.2024; 15(1): 26. CrossRef - ÖZ ŞEFKATİN SOSYAL KAYGI BOZUKLUĞU BELİRTİLERİ İLE İLİŞKİSİNDE BİLİŞSEL ÇARPITMALARIN ARACILIK ROLÜ
Duygu Yücel, Mustafa Batuhan Kurtoğlu
İnönü Üniversitesi Sağlık Hizmetleri Meslek Yüksek Okulu Dergisi.2024; 12(1): 1. CrossRef - Self-regulated learning strategies of tertiary level EFL learners
Ilknur Istifci
Nevşehir Hacı Bektaş Veli Üniversitesi SBE Dergisi.2024; 14(2): 756. CrossRef - Validation of the Arabic Version of the Glasgow Sleep Effort Scale Among Lebanese General Population
Sana Ahmad Tantawi, Lama Ali Alhajj, Atifa Nazih Kamaleddine, Sondos Mohamad Naous, Nafez Nazih Kamaleddine, Issa Kamaleddine, Hussein Walid Mreydem
Sleep Medicine Research.2024; 15(2): 130. CrossRef - Hierarchical-stochastic model predictive control for a grid-interactive multi-zone residential building with distributed energy resources
Felix Langner, Moritz Frahm, Weimin Wang, Jörg Matthes, Veit Hagenmeyer
Journal of Building Engineering.2024; 89: 109401. CrossRef - Analyzing greenhouse gas emissions and influencing factors of 247 actual wastewater treatment plants in China using emission factor and operational data integrated methods (ODIM)
Jiabo Chen, Ziding Ao, Huiling Chen, Yanan Wang, Mei Jiang, Lu Qi, Guohua Liu, Hongchen Wang
Environmental Science and Pollution Research.2024; 31(25): 37387. CrossRef - The chain mediating effect of psychological inflexibility and stress between physical exercise and adolescent insomnia
Qingxin Shen, Shuang Wang, Yang Liu, Zhen Wang, Chenxu Bai, Tiancheng Zhang
Scientific Reports.2024;[Epub] CrossRef - Psychometric characteristics of the career adapt-abilities scale in Thai undergraduate students: a multiple indicators multiple causes model
Buratin Khampirat
Frontiers in Psychology.2024;[Epub] CrossRef - Two sides of a coin: understanding social media use and its relationships to online perceived discrimination and life satisfaction
Mengxuan Cai, Saifuddin Ahmed, Gabrielle C. Ibasco, Arul Chib
Asian Journal of Communication.2024; 34(6): 599. CrossRef - Interpersonalne kognitivne distorzije kao medijator učinka socijalne anksioznosti i depresivnosti na usamljenost studenata
Ana Petak
Primenjena psihologija.2024;[Epub] CrossRef - Psychological resilience and valued living in difficult times: mixed method research in cultural context
Feyza Topçu, Mehmet Dinç
Current Psychology.2024; 43(39): 30595. CrossRef - Psychological Distress and Associated Factors Among Elementary School Teachers: A Cross‐Sectional Study
Farnaz Rahmani, Elnaz Asghari, Reza Naghdi Sadeh, Mina Hosseinzadeh, Leila Gholizadeh
Journal of School Health.2024; 94(11): 1019. CrossRef - Organisational trust, commitment and turnover intention in employees of domestic and foreign banks in Ghana
Thomas Addae Nketsiah, Emmanuel Anokye Nkansah
Cogent Business & Management.2024;[Epub] CrossRef - Assessing knowledge about self-regulated learning: validation of a measurement tool for preschoolers
Lena Grüneisen, Laura Dörrenbächer-Ulrich, Efsevia Kapsali, Franziska Perels
Frontiers in Education.2024;[Epub] CrossRef - Trait Perfectionism, L2 Anxiety, and Willingness to Communicate Among Adolescents: Evaluating the Roles of Worrying About Mistakes and Mistake Rumination
Elyas Barabadi, Gordon L. Flett, Paul L. Hewitt, Seyyed Ayatollah Razmjoo, Mohsen Rahmani Tabar, Fatemeh Chasetareh
Journal of Psychoeducational Assessment.2024; 42(6): 668. CrossRef - Antecedents of E-learning in undergraduate entrepreneurship education
Mavis SB Mensah, Keren NA Arthur, Enoch Mensah-Williams
E-Learning and Digital Media.2024; 21(5): 496. CrossRef - High-speed electric multiple unit trains and tourism in China: service quality impact on passenger satisfaction and loyalty
Bin Zhou, Qihao Xiong, Ping Li, Jianying Jin, Siyi Liu, Chirs Ryan
Tourism Recreation Research.2024; 49(5): 1140. CrossRef - Türkçe Öğrenen Yabancı Öğrencilerin Basamaklı Öğretim Yöntemiyle Üretici Dil Becerilerinin Geliştirilmesi: Bir Eylem Çalışması
Tuncay Türkben, Zahide Gül Koca
Dokuz Eylül Üniversitesi Buca Eğitim Fakültesi Dergisi.2024; (60): 1442. CrossRef - Hwa-byung (anger syndrome) as a risk factor for suicidal ideation in MZ generation: a survey study in South Korea
Chan-Young Kwon
Frontiers in Psychology.2024;[Epub] CrossRef - Saudi undergraduate students’ perceptions of plagiarism: A case of EFL research writing tasks during E-learning sessions
Najah Saad Alsaedi, Mohammad Husam Alhumsi
Heliyon.2024; 10(22): e39804. CrossRef - The Indirect Effect of Future Anxiety on the Relationship between Self-Efficacy and Depression in a Convenience Sample of Adults: Revisiting Social Cognitive Theory
Marta Szota, Aleksandra M. Rogowska, Aleksandra Kwaśnicka, Karolina Chilicka-Hebel
Journal of Clinical Medicine.2024; 13(16): 4897. CrossRef - How does eco-anxiety among geography teachers affect their performance? Evidence from the Banja Luka region (B&H)
Mladjen Trifunovic, Vesna Rajcevic
Journal of the Geographical Institute Jovan Cvijic, SASA.2024; 74(2): 245. CrossRef - “Attrition” versus “intention to stay”: are psychological empowerment and psychological well-being viable retention strategies in the “Great Resignation” context?
Warren Stanley Patrick, Munish Thakur, Jatinder Kumar Jha
International Journal of Organizational Analysis.2024; 32(5): 800. CrossRef - Development and Validation of a Food Systems Knowledge and Attitudes Survey for College Students
Chelsea Allison, Sarah Colby, Wenjun Zhou, Chad Hellwinckel
Journal of Hunger & Environmental Nutrition.2024; 19(2): 217. CrossRef - UP150 Project: A Longitudinal Analysis of Active Lifestyles in the Complex Working System
Gabriele Signorini, Raffaele Scurati, Andrea Bosio, Chiara D’Angelo, Stefano Benedini, Cristina Tringali, Emanuele Magaldi, Marta Rigon, Pietro Luigi Invernizzi
Sports.2024; 12(8): 219. CrossRef - Multi-informant Assessment of Organizational Skills: Psychometric Characteristics of the Children’s Organizational Skills Scale (COSS)
Shannon Ryan, Thomas J. Power, Laura Pendergast, Bridget Poznanski, Jenelle Nissley-Tsiopinis, Howard Abikoff, Richard Gallagher, Katie Tremont, Jaclyn Cacia, Jennifer A. Mautone
School Mental Health.2024; 16(2): 354. CrossRef - Fatigue predicts level of community integration in people with stroke
Lily Y.W. Ho, Cynthia Y.Y. Lai, Claudia K.Y. Lai, Shamay S.M. Ng
Topics in Stroke Rehabilitation.2024; 31(5): 464. CrossRef - Love as a Commitment Device
Marta Kowal, Adam Bode, Karolina Koszałkowska, S. Craig Roberts, Biljana Gjoneska, David Frederick, Anna Studzinska, Dmitrii Dubrov, Dmitry Grigoryev, Toivo Aavik, Pavol Prokop, Caterina Grano, Hakan Çetinkaya, Derya Atamtürk Duyar, Roberto Baiocco, Carlo
Human Nature.2024; 35(4): 430. CrossRef - Effect of teachers’ teaching strategies on students’ learning engagement: moderated mediation model
Heping Zhang, Junjie Yang, Zhiyuan Liu
Frontiers in Psychology.2024;[Epub] CrossRef - I want to be safe: understanding the main drivers behind vaccination choice throughout the pandemic
Marco Marini, Alessandro Demichelis, Dario Menicagli, Giovanna Mancini, Folco Panizza, Ennio Bilancini, Gustavo Cevolani
BMC Public Health.2024;[Epub] CrossRef - Reconstructing Pinch Strength after Ulnar Nerve Injury by Transferring the Opponens Pollicis Motor Branch
Jayme Augusto Bertelli
Plastic & Reconstructive Surgery.2024; 154(2): 351. CrossRef - People Declare Lowered Levels of Sociosexual Desire in the Presence of an Attractive Audience
Michal Mikolaj Stefanczyk
Archives of Sexual Behavior.2024; 53(3): 879. CrossRef - Pathways from morphological awareness to reading fluency: the mediating role of phonological awareness and vocabulary
Sophia Giazitzidou, Angeliki Mouzaki, Susana Padeliadu
Reading and Writing.2024; 37(5): 1109. CrossRef - Associations with smartphone usage and life satisfaction among older adults: Mediating roles of depressive symptoms and cognitive function
Ha Na Jeong, Sun Ju Chang, Soyeon Kim
Geriatric Nursing.2024; 55: 168. CrossRef - The impact of parental acceptance and childhood maltreatment on mental health and physical pain in Burundian survivors of childhood sexual abuse
Julia Schneider, Anja C. Rukundo-Zeller, Manassé Bambonyé, Sarah Lust, Hervé Mugisha, Jean-Arnaud Muhoza, Thierry Ndayikengurukiye, Lydia Nitanga, Amini Ahmed Rushoza, Anselm Crombach
Child Abuse & Neglect.2024; 154: 106906. CrossRef - The Impact of Student-Centered Teaching Strategies on Educational Attainment in Econometrics: Evidence From the UK
Imran Hussain Shah, Audrey Au Yong Lyn, Guillaume Maxence Augustin Morlet, Ladina Rageth
Sage Open.2024;[Epub] CrossRef - Facial impression of trustworthiness biases statement credibility unless suppressed by facemask
Marco Marini, Fabio Paglieri, Alessandro Ansani, Fausto Caruana, Marco Viola
Current Psychology.2024; 43(14): 13072. CrossRef - The Association between Physical Frailty and Cognitive Performance in Older Adults Aged 60 to 96 Years: Data from the “Good Aging in Skåne” (GÅS) Swedish Population Study
Katrina Lundberg, Sölve Elmståhl, Lena Sandin Wranker, Henrik Ekström
Annals of Geriatric Medicine and Research.2024; 28(3): 330. CrossRef - Behavioral Disorders of Spatial Cognition in Patients with Mild Cognitive Impairment Due to Alzheimer’s Disease (The BDSC-MCI Project): Ecological Validity of the Corsi Learning Suvra-Span Test
Davide Maria Cammisuli, Gloria Marchesi, Virginia Bellocchio, Edoardo Nicolò Aiello, Barbara Poletti, Federico Verde, Vincenzo Silani, Nicola Ticozzi, Stefano Zago, Teresa Difonzo, Valeria Isella, Simone Pomati, Valentina Granese, Benedetta Vignati, Loren
Journal of Personalized Medicine.2024; 14(5): 539. CrossRef - Further psychometric validation and test–retest reproducibility of the WOUND‐Q
Nina Vestergaard Simonsen, Anne F. Klassen, Charlene Rae, Farima Dalaei, Stefan Cano, Lotte Poulsen, Andrea L. Pusic, Jens Ahm Sørensen
International Wound Journal.2024;[Epub] CrossRef - Try not to think about food: An association between fasting, binge eating and food cravings
Jônatas de Oliveira, João Ferro, Victor Hugo Dantas Guimarães, Felipe Quinto da Luz
Journal of the National Medical Association.2024; 116(5): 588. CrossRef - Exploring the relationships among fear of missing out (FoMO), sensation seeking and leisure activity participation
Mehpare Tokay Argan, Funda Koçak, Bülent Gürbüz, Metin Argan, Halime Dinç
World Leisure Journal.2024; 66(2): 165. CrossRef - Investigating the mediating role of emotional intelligence in the relationship between internet addiction and mental health among university students
Girum Tareke Zewude, Derib Gosim, Seid Dawed, Tilaye Nega, Getachew Wassie Tessema, Amogne Asfaw Eshetu, Calvin Or
PLOS Digital Health.2024; 3(11): e0000639. CrossRef - Large‐scale investigation of white matter structural differences in bilingual and monolingual children: An adolescent brain cognitive development data study
Juliana Ronderos, Jennifer Zuk, Arturo E. Hernandez, Kelly A. Vaughn
Human Brain Mapping.2024;[Epub] CrossRef - From Clicks to Credits: Examining the Influence of Online Engagement and Internet Addiction on Academic Performance in Chinese Universities
Yongzhong Jiang, Dirgha Raj Joshi, Jeevan Khanal
SSRN Electronic Journal.2024;[Epub] CrossRef - Psychometric Properties of the Strength-based Parenting Questionnaire Parent-version in Malaysia
Clarisse Roswini Kalaman, Norhayati Ibrahim, Choy Qing Cham, Meng Chuan Ho, Yan-Li Siaw, Amira Najiha Yahya, Ching Sin Siau
Pertanika Journal of Social Sciences and Humanities.2024; 32(4): 1345. CrossRef - Development of the Life-Worldly Communication Scale to Improve Quality of Life: Daily Conversation as Care for Older Adults
Yasuko Fukaya, Minato Kawaguchi, Meiko Okabe, Sachiyo Koyama, Takanori Kitamura
Health Communication.2024; 39(9): 1727. CrossRef - Students’ gender differences and scientific inquiry competencies in technical education and training institutions
Labani Kanyonga, Eugenia J. Kafanabo, Sammy K. Chumba, David Kipkasi Kessio
International Journal of Science Education.2024; : 1. CrossRef - Psychometric properties of the Motors of Mpox Vaccination Acceptance Scale among men who have sex with men
Chung-Ying Lin, Ching-Shu Tsai, Mark D. Griffiths, Chien-Wen Lin, Cheng-Fang Yen
Human Vaccines & Immunotherapeutics.2024;[Epub] CrossRef - A serial mediation model of Big 5 personality traits, emotional intelligence, and psychological capital as predictors of teachers' professional well-being
Girum Tareke Zewude, Yikunoamlak Mesfin, Fatiha Sadouki, Abate Getahun Ayele, Solomon Goraw, Tesfaye Segon, Mária Hercz
Acta Psychologica.2024; 250: 104500. CrossRef - Holistic shape variation of the rib cage in an adult population
Andrea Robinson, Bowen Zheng, B. Wade von Kleeck, Josh Tan, F. Scott Gayzik
Frontiers in Bioengineering and Biotechnology.2024;[Epub] CrossRef - Is adding resources always beneficial? Multiplicative impact of psychological capital and goal-oriented climate on Spanish public worker satisfaction and engagement
Pedro Antonio Díaz-Fúnez, Giuseppina María Cardella, Brizeida Raquel Hernández-Sánchez, José Carlos Sánchez-García, Miguel Ángel Mañas-Rodríguez
Frontiers in Psychology.2024;[Epub] CrossRef - Validation of the Internet entrepreneurial self-efficacy scale among Romanian technical students
Beatrice Adriana Balgiu, Daniela Maricica Cotoară, Andrei Simionescu-Panait, Ioana Gutu
PLOS ONE.2024; 19(10): e0312929. CrossRef - How Islamic work ethics predict work engagement: a double mediation model
Sheema Tarab
Society and Business Review.2024; 19(4): 743. CrossRef - The intention to adopt metaverse in Islamic banks: an integrated theoretical framework of TAM and religiosity intention model
Hashem Alshurafat, Omar Arabiat, Maha Shehadeh
Journal of Islamic Marketing.2024;[Epub] CrossRef - Self-guides, enjoyment, gender, and achievement: a survey of Chinese EFL high school students
Eerdemutu Liu, Junju Wang, Sachurina Bai
Journal of Multilingual and Multicultural Development.2024; 45(10): 4270. CrossRef - Çalışanların Örgütsel Bağlılık İle Örgütsel Özdeşleşme Davranışının Yeşil Örgütsel Davranış Üzerindeki Etkisinde Çevre Tutkusunun Aracı Rolü
Habibe REŞAT CİCA, Tuğba KARABULUT
Gaziantep University Journal of Social Sciences.2024; 23(1): 304. CrossRef - Accumulation of potentially toxic elements in fourfinger threadfin (Eleutheronema tetradactylum) and black pomfret (Parastromateus niger) from Selangor, Malaysia
Peggy Pei Yee Tek, Chuck Chuan Ng
Environmental Monitoring and Assessment.2024;[Epub] CrossRef - ENTREPRENEURIAL TRAITS AS CATALYSTS FOR PRIVATE ECONOMIC DEVELOPMENT: INSIGHTS FROM VIETNAM
THANG LOI NGO, QUOC DUNG NGO
Journal of Developmental Entrepreneurship.2024;[Epub] CrossRef - Engagement in sports and children's cognitive abilities: An analysis of executive functions
Nataša Buha, Bojan Dučić, Mirjana Japundža-Milisavljević
Inovacije u nastavi.2024; 37(4): 17. CrossRef - Síntomas de ansiedad y depresión en una muestra de la población general: el efecto mediador de los pensamientos negativos repetitivos, la supresión de pensamientos, la reevaluación positiva y la resistencia al malestar
Manuel González, Mario González, Anna Rovella
Diversitas.2024; 20(1): 16. CrossRef - Effect of Arogya Raksha Panchatantra (five lifestyle principles) on heart rate variability, menstrual symptoms, health-related quality of life, performance and self-efficacy in Young female adults with primary dysmenorrhea: protocol for an exploratory ran
Karishma Silwal, Prakash Babu Kodali, Vakeel Khan, Hemanshu Sharma, Gulab Rai Tewani, Pradeep M. K. Nair
CCRYN Indian Journal of Yoga & Naturopathy.2024; 1(1): 15. CrossRef - Development and Validation of a Short Form of the German Self-Consciousness Scale for the General Population
Kyla Brophy, Matthew Emery, Adina Coroiu, Cornelia Albani, Elmar Braehler, Annett Körner
European Journal of Psychology Open.2024; 83(4): 173. CrossRef - The Relationship of Frailty with Psychopathology, Childhood Traumas and Insecure Attachment in Young Adults: A Cross-Sectional Investigation
Francesco Saverio Bersani, M. Canevelli, C. Imperatori, B. Barchielli, E. Prevete, F. Sciancalepore, R. Vicinanza, A. Maraone, M. Salzillo, L. Tarsitani, S. Ferracuti, M. Pasquini, G. Bruno
The Journal of Frailty & Aging.2024; 13(4): 448. CrossRef - İyimserlik ve kötümserlik düzeylerinin yaşam amacı ve yaşam doyumu ilişkisinde aracı rolü
Sena Daşkıran, Ayça Nur Dişkaya, Osman Tolga Arıcak
Klinik Psikoloji Dergisi.2024; 8(3): 320. CrossRef - 중학생의 운동시간이 행복감에 미치는 영향: 그릿(Grit)과 자아존중감의 순차적 매개효과
주형 김, 성호 권, 승주 이
The Korean Journal of Physical Education.2024; 63(6): 473. CrossRef - Linking Perceived Risk of Public Health Emergency to Psychological Distress among Chinese College Students: The Chain Mediation Role of Balanced Time Perspective and Negative Coping Styles
Biru Chang, Shengqiang Zhu, Qian Xie, Yanghui Dai
International Journal of Mental Health Promotion.2024; 26(8): 599. CrossRef - Assessing Antecedents of Prospective Accountant Ethical Behaviour across Demographics: The Case of Accounting Students in Ghana
Samuel Kwarteng, Israel Duodu, Charles Omane-Adjekum, Adjei Frimpong, Emmanuel Quayson
SCIENCE MUNDI.2024; 4(2): 259. CrossRef - A Structural Equation Modeling Analysis of Key Factors: Enhancing Urban Community in the Southwest China
Zai Xiaona, Sujitta Suraphee, Chom Panta, Thom Gatewongsa, Piyapatr Busababodhin
Lobachevskii Journal of Mathematics.2024; 45(12): 6440. CrossRef - Citizen perceptions of digital transformation in local municipalities: The case of South Africa
Vusani Netshirando, Willard Munyoka, Armstrong Kadyamatimba
South African Journal of Information Management.2024;[Epub] CrossRef - Internet Gaming Disorder and Mental Health of Children in China: A Latent Profile Analysis
Md Zahir Ahmed, Oli Ahmed, Lingfeng Gao, Mary C. Jobe, Weijian Li
International Journal of Mental Health Promotion.2024; 26(7): 517. CrossRef - Exploring the Interplay between Job Stress, Work Performance, and Attitudes toward Professional Psychological Help among Employees
Cong Minh Le, Son Van Huynh, Ky Luu, Quynh-Nhi Ngoc Ho, Van Thi Le Nguyen, Vinh-Long Tran-Chi
International Journal of Mental Health Promotion.2024; 26(7): 531. CrossRef - The Social Networking Addiction Scale: Translation and Validation Study among Chinese College Students
Siyuan Bi, Junfeng Yuan, Lin Luo
International Journal of Mental Health Promotion.2024; 26(1): 51. CrossRef - From Family Conflicts to Suicide Risk Through Deliberate Self-Harm Online Content in Adolescents and Young Adults
Beatriz Fuschini, Eva Duarte, Mariana P. Miranda, Maria Gouveia-Pereira
European Journal of Mental Health.2024; 19: 1. CrossRef - Comparison of the Brief Interview for Mental Status (BIMS) and Montreal Cognitive Assessment (MoCA) for identifying cognitive impairments and predicting rehabilitation outcomes in an inpatient rehabilitation facility
Erin Y. Harmon, Robert W. Gillen
PM&R.2023; 15(9): 1083. CrossRef - Real-world trial of positive youth development program “LifeMatters” with South African adolescents in a low-resource setting
Daniel Thomas Page, Stephanie Hanrahan, Lisa Buckley
Children and Youth Services Review.2023; 146: 106818. CrossRef - Cerebral blood flow and immediate and sustained executive function benefits following single bouts of passive and active exercise
Benjamin Tari, Joshua Ahn, Connor Dalton, Sun Young Choo, Matthew Heath
Brain and Cognition.2023; 166: 105953. CrossRef - School Demands and Resources as Predictors of Student Burnout Among High School Students
Balázs Jagodics, Katalin Nagy, Szilvia Szénási, Ramóna Varga, Éva Szabó
School Mental Health.2023; 15(1): 90. CrossRef - Factors Associated With Patient Satisfaction Measured Using an Iterative Scale
Yvonne Versluijs, Amirreza Fatehi, Amanda I. Gonzalez, Lee Reichel, David Laverty, David Ring
Quality Management in Health Care.2023; 32(2): 69. CrossRef - Students’ perceptions of pedagogy for 21st century learning instrument (S-POP-21): Concept, validation, and initial results
Dr Aibhín Bray, Dr Carina Girvan, Eilís Ní Chorcora
Thinking Skills and Creativity.2023; 49: 101319. CrossRef - Group Belonging and Social Identities in the Transition of Asylum-Seekers in Greece: Longitudinal Pathways to Adjustment
Angelos Panagiotopoulos, Vassilis Pavlopoulos
Healthcare.2023; 12(1): 55. CrossRef - Enablers for Adopting Restriction of Hazardous Substances Directives by Electronic Manufacturing Service Providers
Jeng-Chieh Cheng, Jeen-Fong Li, Chi-Yo Huang
Sustainability.2023; 15(16): 12341. CrossRef - Longitudinal Association between Maternal Autonomy Support and Controlling Parenting and Adolescents’ Depressive Symptoms
Ayumi Tanaka, Ayame Tamura, Ryo Ishii, Shin-ichi Ishikawa, Naoki Nakazato, Kazuhiro Ohtani, Michiko Sakaki, Takashi Suzuki, Kou Murayama
Journal of Youth and Adolescence.2023; 52(5): 1058. CrossRef - Dietary trends among young adults during the COVID-19 lockdown: socioeconomic and gender disparities
Jennifer Parker, Simranpreet Kaur, John Marlo Medalla, Anairobi Imbert-Sanchez, Jeanette Bautista
BMC Nutrition.2023;[Epub] CrossRef - A Prospective Study to Examine Responsiveness and Minimally Important Differences (MIDs) for the CLEFT-Q Scales Following Three Cleft-Specific Operations
A Miroshnychenko, C Rae, K Wong Riff, CR Forrest, T Goodacre, MC Swan, R Slator, J Goldstein, A Thoma, K Harman, A Klassen
The Cleft Palate Craniofacial Journal.2023; 60(4): 413. CrossRef - Clinimetrics of the cognitive section of the Italian ALS Cognitive Behavioral Screen (ALS-CBS™)
Edoardo Nicolò Aiello, Lucia Catherine Greco, Antonino La Tona, Federica Solca, Silvia Torre, Laura Carelli, Debora Pain, Alice Radici, Andrea Lizio, Jacopo Casiraghi, Federica Cerri, Agostino Brugnera, Angelo Compare, Susan Woolley, Jennifer Murphy, Luci
Neurological Sciences.2023; 44(4): 1243. CrossRef - Is Activation the Active Ingredient of Transdiagnostic Therapies? A Randomized Clinical Trial of Behavioral Activation, Acceptance and Commitment Therapy, and Transdiagnostic Cognitive-Behavioral Therapy for Emotional Disorders
Concepción Fernández-Rodríguez, Rocio Coto-Lesmes, Victor Martínez-Loredo, Sonia González-Fernández, Marcelino Cuesta
Behavior Modification.2023; 47(1): 3. CrossRef - Promoting pro‐environmental behavior through organizational identity and green organizational climate
Hina Zafar, Jo Ann Ho, Jun‐Hwa Cheah, Rosmah Mohamed
Asia Pacific Journal of Human Resources.2023; 61(2): 483. CrossRef - “So, Why Were You Late Again?”: Social Account’s Influence on the Behavioral Transgression of Being Late to a Meeting
Joseph A. Allen, Emilee Eden, Katherine C. Castro, McKaylee Smith, Joseph E. Mroz
Merits.2023; 3(3): 459. CrossRef - Exploring the attitude of youth towards adventure tourism as a driver for post-pandemic era tourism experiences
Nicolae Al. Pop, Felicia A. Stăncioiu, Lucian-Florin Onișor, Cristina Andrada Baba, Raluca Năstase Anysz
Current Issues in Tourism.2023; 26(7): 1147. CrossRef - Association between childhood trauma, intimate partner violence, and perceived parental competence among women abusing amphetamine-type stimulant
Suzaily Wahab, Rubini Sivarajah, Amirul Danial Azmi, Norliza Chemi, Raynuha Mahadevan
Frontiers in Psychiatry.2023;[Epub] CrossRef - Technology integration in emergency remote teaching: teachers’ self-efficacy and sense of success
Arnon Hershkovitz, Ella Daniel, Yasmin Klein, Malka Shacham
Education and Information Technologies.2023; 28(10): 12433. CrossRef - US college student mental health and COVID-19: Comparing pre-pandemic and pandemic timepoints
Patricia Frazier, Yuchen Liu, Alexa Asplund, Liza Meredith, Viann N. Nguyen-Feng
Journal of American College Health.2023; 71(9): 2686. CrossRef - Psychometric validation of the sibling inventory of behavior in three- to six-year-old Chinese children
Huiyan Xu, Zhenlin Wang, Xiaozi Gao, Xiaoying Wang, Qiong Wu
Frontiers in Psychology.2023;[Epub] CrossRef - Dissociative experiences of compartmentalization are associated with food addiction symptoms: results from a cross‐sectional report
Giuseppe Alessio Carbone, Elena De Rossi, Elisabeth Prevete, Lorenzo Tarsitani, Ornella Corazza, Chiara Massullo, Benedetto Farina, Massimo Pasquini, Ines Taddei, Massimo Biondi, Claudio Imperatori, Francesco Saverio Bersani
Eating and Weight Disorders - Studies on Anorexia, Bulimia and Obesity.2023;[Epub] CrossRef - Improving stress management, anxiety, and mental well-being in medical students through an online Mindfulness-Based Intervention: a randomized study
Teresa Fazia, Francesco Bubbico, Andrea Nova, Chiara Buizza, Herald Cela, Davide Iozzi, Beril Calgan, Federica Maggi, Valentina Floris, Irene Sutti, Salvatore Bruno, Alberto Ghilardi, Luisa Bernardinelli
Scientific Reports.2023;[Epub] CrossRef - Parental overcontrol is associated with dysmorphic concern severity: A cross-sectional study
Elena De Rossi, Benedetto Farina, Mauro Adenzato, Giuseppe Alessio Carbone, Rita B. Ardito, Claudio Imperatori
Journal of Affective Disorders.2023; 343: 96. CrossRef - Enhancing Consumer Confidence and Response Efficacy in Tourism: Typology and Effectiveness of the Hotel Industry’s Responses to COVID-19
Hyunsu Kim, Jing Li, Kevin Kam Fung So
Journal of Travel Research.2023; 62(4): 907. CrossRef - Assessment of Cardiovascular Risk and Arterial Stiffness in Patients With Human Immunodeficiency Virus
Mariana Freitas, Clarisse Neves, Helena Sarmento, Pedro Cunha, Jorge Cotter
Cureus.2023;[Epub] CrossRef - Sleep characteristics and pain in middle-aged and older adults: Sex-specific impact of physical and sitting activity
Amy N. Costa, Adriana Coman, Madison Musich, Jeeeun Park, David Q. Beversdorf, Christina S. McCrae, Ashley F. Curtis
Sleep Medicine.2023; 111: 180. CrossRef - Psychometric Analysis and Validation of the Italian Bergen Facebook Addiction Scale
Paolo Soraci, Ambra Ferrari, Nadia Barberis, Giuseppe Luvarà, Antonino Urso, Elena Del Fante, Mark D. Griffiths
International Journal of Mental Health and Addiction.2023; 21(1): 451. CrossRef - Moderators of the cost-effectiveness of transdiagnostic CBT for anxiety disorders over an 8-month time horizon using a net-benefit regression framework
Alexandra Chapdelaine, Helen-Maria Vasiliadis, Martin D. Provencher, Peter J. Norton, Pasquale Roberge
BMC Health Services Research.2023;[Epub] CrossRef - Autonomous learning and the use of digital technologies in online English classrooms in higher education
Damar Isti Pratiwi, Budi Waluyo
Contemporary Educational Technology.2023; 15(2): ep423. CrossRef - Development and Validation of a Patient-Reported Outcome Measure for Fingernail and Toenail Conditions: The NAIL-Q
Anne Klassen, Charlene Rae, Maureen O'Malley, Trisia Breitkopf, Leah Algu, Jasmine Mansouri, Claire Brown, Yi Wang, Shari Lipner
Clinical, Cosmetic and Investigational Dermatology.2023; Volume 16: 3091. CrossRef - Time-frequency analysis of differences between coordinates of three permanent GNSS stations in Krakow
Wiesław Kosek, Zbigniew Siejka
Reports on Geodesy and Geoinformatics.2023; 116(1): 61. CrossRef - University teachers’ profiles based on digital innovativeness and instructional adaptation to COVID-19: Association with learning patterns and teacher demographics
Tahani Z. Aldahdouh, Mari Murtonen, Jere Riekkinen, Henna Vilppu, Trang Nguyen, Petri Nokelainen
Education and Information Technologies.2023; 28(11): 14473. CrossRef - Self-criticism and self-compassion as mediators of the relationship between alexithymia and postpartum depressive symptoms
Ana-Maria Andrei, Rebecca Webb, Violeta Enea
Psihologija.2023; 56(2): 145. CrossRef - Effect of Family Cohesion on Depression of Chinese College Students in the COVID-19 Pandemic: Chain Mediation Effect of Perceived Social Support and Intentional Self-Regulation
Jingjing Wang, Xiangli Guan, Yue Zhang, Yang Li, Md Zahir Ahmed, Mary C. Jobe, Oli Ahmed
International Journal of Mental Health Promotion.2023; 25(2): 223. CrossRef - Ideal L2 Self, Self-Efficacy, and Pragmatic Production: The Mediating Role of Willingness to Communicate in Learning English as a Foreign Language
He Yang, Zheyu Lian
Behavioral Sciences.2023; 13(7): 597. CrossRef - Coach perceptions of child safeguarding policy in New Zealand’s youth sport sector
Blake Bennett, Shengnan Wang, Glenn Fyall
Sports Coaching Review.2023; : 1. CrossRef - Risk factors for Internet Gaming Disorder: Testing the contribution of metacognitions, stress, and coping
Hui Zhou, Le Dang, Adrian Wells, Anise M.S. Wu
Addictive Behaviors.2023; 147: 107836. CrossRef - Examining promotive and protective effects of ethnic identity on alcohol and cannabis use among Black young adults
Tamika C.B. Zapolski, Venessannah A. Deppermann
Journal of Substance Use and Addiction Treatment.2023; 153: 209009. CrossRef - Factors influencing construction workers’ intention to transfer occupational health and safety training
Thanh Tung Pham, Helen Lingard, Rita Peihua Zhang
Safety Science.2023; 167: 106288. CrossRef - Photovoltaic Cell Panels Soiling Inspection Using Principal Component Thermal Image Processing
A. Sriram, T. D. Sudhakar
Computer Systems Science and Engineering.2023; 45(3): 2761. CrossRef - Characteristics and Outcomes of COVID-19 Survivors Requiring Inpatient Rehabilitation
Sergo Gabunia, Erin Y. Harmon, Matthew B. Sonagere, Amy E. Teale
American Journal of Physical Medicine & Rehabilitation.2023; 102(3): 206. CrossRef - Attitude and behaviour of soft contact lens wearers toward compliance in Gauteng, South Africa
Tania B. Noach, Thokozile I. Metsing, Dirk Booysen
African Vision and Eye Health.2023;[Epub] CrossRef - Profiles of historical loss and childhood trauma as predictors of mental and cardiometabolic health in American Indian adults
Neha A. John-Henderson, Annie T. Ginty
SSM - Mental Health.2023; 4: 100252. CrossRef - Development of a Novel Ground Test Facility for Aircraft Environmental Control System
Shafayat Hasan Chowdhury, Fakhre Ali, Ian K. Jennions
Journal of Thermal Science and Engineering Applications.2023;[Epub] CrossRef - #ProblematicInstaUser: Motivations and the mediating role of fear of missing out among young adults
Juhyung Sun
Current Psychology.2023; 42(17): 14919. CrossRef - The effects of cannabidiol on worry and anxiety among high trait worriers: a double-blind, randomized placebo controlled trial
L. Riley Gournay, Morgan L. Ferretti, Sarah Bilsky, Emily Vance, Anna Marie Nguyen, Eric Mann, Parker Williams, Ellen W. Leen-Feldner
Psychopharmacology.2023; 240(10): 2147. CrossRef - A methodological comparison of discriminant function analysis and binary logistic regression for estimating sex in forensic research and case-work
Deepika Rani, Kewal Krishan, Tanuj Kanchan
Medicine, Science and the Law.2023; 63(3): 227. CrossRef - Translating spatial navigation evaluation from experimental to clinical settings: The virtual environments navigation assessment (VIENNA)
Sophia Rekers, Carsten Finke
Behavior Research Methods.2023; 56(3): 2033. CrossRef - Rational or emotional? A study on Chinese tourism boycotts on social media during international crisis situations
Xueting Zhai, Qiuju Luo
Tourism Management Perspectives.2023; 45: 101069. CrossRef - An Empirical Investigation on Healthcare Professionals' Work Ethic and Ethical Attitudes: The Impact of Leadership Qualities on Ethics Construct and Professional Behaviors
Dr. Dhakshayini K. N, Ms. Priyanka G
International Journal of Advanced Research in Science, Communication and Technology.2023; : 190. CrossRef - The relationship between biophilia levels of preschoolers and social-emotional well-being and psychological resilience in the context of age and gender
İlknur Tarman, Filiz Erbay, Neslihan Durmusoglu-Saltali
Early Child Development and Care.2023; 193(8): 1041. CrossRef - The construction and preliminary validation of a new Pictorial Materialism Test for 4–6-year-old children
Agata Trzcińska, Karolina Kubicka, Wojciech Podsiadłowski, Rizwan Ahmed Laar
PLOS ONE.2023; 18(8): e0290512. CrossRef - Antecedents of Behavioral Intentions for Purchasing Hybrid Cars Using Sustainability Theory of Planned Behavior Integrated with UTAUT2
Ardvin Kester S. Ong, Josephine D. German, Anak Agung Ngurah Perwira Redi, Lara Nicole Z. Cordova, Franscine Althea B. Longanilla, Neallo L. Caprecho, Rocksel Andry V. Javier
Sustainability.2023; 15(9): 7657. CrossRef - Effects of Expert Modeling Videos on the Development of Nursing Students' Clinical Competence
Tracy M. Dodson
Journal of Nursing Education.2023; 62(8): 454. CrossRef - The Effect of Pre-Service Teachers’ Family Adaptation on Anxiety: A Moderated Mediating Effect
Xuejiao Li, Xiangli Guan, Jingjing Wang, Yaqi Zhang, Miqi Ma, Tong Pu, Mary C. Jobe, Md Zahir Ahmed
Sustainability.2023; 15(14): 10796. CrossRef - Hopelessness in caregivers of children with attention-deficit/hyperactivity disorder: Associations with depression and anxiety and multidimensionally related factors
Tai-Ling Liu, Ray C. Hsiao, Wen-Jiun Chou, Cheng-Fang Yen
Journal of the Formosan Medical Association.2023; 122(11): 1158. CrossRef - Standardization of the Italian ALS-CBS™ Caregiver Behavioral Questionnaire
Edoardo Nicolò Aiello, Federica Solca, Lucia Catherine Greco, Antonino La Tona, Silvia Torre, Laura Carelli, Claudia Morelli, Alberto Doretti, Eleonora Colombo, Stefano Messina, Debora Pain, Alice Radici, Andrea Lizio, Jacopo Casiraghi, Federica Cerri, Ag
Frontiers in Psychology.2023;[Epub] CrossRef - Exploring Effective Relationships Between Visual-Audio Channels in Data Visualization
Sadia Rubab, Lingyun Yu, Junxiu Tang, Yingcai Wu
Journal of Visualization.2023; 26(4): 937. CrossRef - Moderate Alcohol Consumption and Depression: A Marginal Structural Model Approach Promoting Causal Inference
Rachel Visontay, Louise Mewton, Tim Slade, Izzuddin M. Aris, Matthew Sunderland
American Journal of Psychiatry.2023; 180(3): 209. CrossRef - Examination of the relationship between information and communication technology competencies and communication skills
Olga V. Sergeeva, Marina R. Zheltukhina, Goliya I. Bikbulatova, Ekaterina G. Sokolova, Olesya Yu Digtyar, Alexey I. Prokopyev, Zhanna M. Sizova
Contemporary Educational Technology.2023; 15(4): ep483. CrossRef - Motivations for Proactive and Reactive Trolling on Social Media: Developing and Validating a Four-Factor Model
Yuanyi Mao, Tianyi Xu, Ki Joon Kim
Social Media + Society.2023;[Epub] CrossRef - Risk factors associated with occupational noise-induced hearing loss in the Hispanic community health study/study of Latinos: A cross-sectional epidemiologic investigation
Michelle L. Arnold, Victoria A. Sanchez, Danielle Nichole Carrasco, Diane Martinez, Sumitrajit Dhar, Ariana Stickel, Krista M. Perreira, Tsalatsanis Athanasios, David J. Lee
Journal of Occupational and Environmental Hygiene.2023; 20(12): 586. CrossRef - Yönetici Nezaketsizliğinin Örgütsel Vatandaşlık Davranışına Etkisi: Psikolojik Sözleşme İhlali ve Ahlaki Çözülmenin Aracılık Rolü
Selen Doğan, Fatma Gül Karaçelebi
İş ve İnsan Dergisi.2023; 10(2): 125. CrossRef - Physical accessibility in Malaysian higher educational institutions: Voices of students with disabilities
Cheong Chong Chan, Yusmarhaini Yusof, Fatimah Zailly Ahmad Ramli, Azlin Hilma Hillaluddin, Zarina Mat Saad
International Social Work.2023; 66(6): 1669. CrossRef - Citizens' intentions to use e-government during the COVID-19 pandemic: integrating the technology acceptance model and perceived risk theory
Thi Thanh Truc Nguyen
Kybernetes.2023; 52(7): 2329. CrossRef - A Screening Tool for Exercise Addiction: The Psychometric Properties of the Italian Exercise Addiction Inventory
Alessio Gori, Eleonora Topino, Mark D. Griffiths
International Journal of Mental Health and Addiction.2023; 21(3): 1618. CrossRef - Academic word difficulty and multidimensional lexical sophistication: An English‐for‐academic‐purposes‐focused conceptual replication of Hashimoto and Egbert (2019)
Joseph P. Vitta, Christopher Nicklin, Simon W. Albright
The Modern Language Journal.2023; 107(1): 373. CrossRef - Prevalence and determinants of language impairment in non‐demented amyotrophic lateral sclerosis patients
Federica Solca, Edoardo Nicolò Aiello, Silvia Torre, Laura Carelli, Roberta Ferrucci, Federico Verde, Nicola Ticozzi, Vincenzo Silani, Alessia Monti, Barbara Poletti
European Journal of Neurology.2023; 30(3): 606. CrossRef - Career flexibility and its relation to time perspective: a study with college students in the Portuguese context
Juliana Frainer, Isabel N. Janeiro
Frontiers in Psychology.2023;[Epub] CrossRef - The development and validation of the assessment engagement scale
Carol Evans, Xiaotong Zhu
Frontiers in Psychology.2023;[Epub] CrossRef - Psychodiagnostics of Value Orientations of Adolescents: the Results of Standardization of the Methodology "Hierarchy of Life Values" by G.V. Rezapkina
O.A. Ulyanina, N.P. Radchikova, E.V. Borisenko, Z.R. Khayrova
Social Psychology and Society.2023; 14(3): 154. CrossRef - The role of country of origin image, brand image and eWOM in the intention to receive the Sinopharm vaccine
Davood Ghorbanzadeh, Muhammad Salman Shabbir
Journal of Social Marketing.2023; 13(2): 172. CrossRef - Power-law initialization algorithm for convolutional neural networks
Kaiwen Jiang, Jian Liu, Tongtong Xing, Shujing Li, Shunyao Wu, Fengjing Shao, Rencheng Sun
Neural Computing and Applications.2023; 35(30): 22431. CrossRef - Perceptions of the Benefits and Barriers to Vegetarian Diets and the Environmental Impact of Meat-Eating
Ashley Rattenbury, Matthew B. Ruby
Sustainability.2023; 15(21): 15522. CrossRef - Revisiting the relationships of n-gram measures to L2 writing proficiency: Comparisons between genres and connections to vocabulary levels
Lingmin Huang, Yuanke Li
System.2023; 118: 103136. CrossRef - Din Öğretimi Öğretmen Adaylarının Bilişsel Esneklik Düzeyleri ile Eleştirel Düşünme Eğilimlerinin İncelenmesi
Zeynep DEMİRTAŞ, Mithat TAKUNYACI, Rüştü YEŞİL
Hitit İlahiyat Dergisi.2023; 22(2): 723. CrossRef - Household smoking impact on the oral health of 5- to 7-years-old children
Abla Arafa
BMC Oral Health.2023;[Epub] CrossRef - Psychophysiological fidelity: A comparative study of stress responses to real and simulated clinical emergencies
Russell Peek, Lee Moore, Rachel Arnold
Medical Education.2023; 57(12): 1248. CrossRef - Soft skills and knowledge required for a professional accountant: Evidence from Jordan
Sally Abu Asabeh, Raneem Alzboon, Rahaf Alkhalaileh, Hashem Alshurafat, Hamzeh Al Amosh
Cogent Education.2023;[Epub] CrossRef - How human-automation interaction experiences, trust propensity and dynamic trust affect drivers’ physiological responses in conditionally automated driving: Moderated moderated-mediation analyses
Binlin Yi, Haotian Cao, Xiaolin Song, Jianqiang Wang, Wenfeng Guo, Zhi Huang
Transportation Research Part F: Traffic Psychology and Behaviour.2023; 94: 133. CrossRef - Affective touch in anorexia nervosa: Exploring the role of social anhedonia and lifespan experiences
Sofia Tagini, Ilaria Bastoni, Valentina Villa, Leonardo Mendolicchio, Gianluca Castelnuovo, Alessandro Mauro, Federica Scarpina
Journal of Affective Disorders.2023; 324: 607. CrossRef - Mother-child and father-child “serve and return” interactions at 9 months: Associations with children’s language skills at 18 and 24 months
Yu Chen, Natasha J. Cabrera, Stephanie M. Reich
Infant Behavior and Development.2023; 73: 101894. CrossRef - Person-environment fit and task performance: exploring the role(s) of grit as a personal resource
Llewellyn E. van Zyl, H. A. van Vuuren, Lara C. Roll, Marius W. Stander
Current Psychology.2023; 42(27): 23560. CrossRef - Clinimetrics and feasibility of the Italian version of the Frontal Assessment Battery (FAB) in non-demented Parkinson’s disease patients
Edoardo Nicolò Aiello, Alfonsina D’Iorio, Federica Solca, Silvia Torre, Ruggero Bonetti, Francesco Scheveger, Eleonora Colombo, Alessio Maranzano, Luca Maderna, Claudia Morelli, Alberto Doretti, Marianna Amboni, Carmine Vitale, Federico Verde, Roberta Fer
Journal of Neural Transmission.2023; 130(5): 687. CrossRef - Aging With Incarceration Histories: An Intersectional Examination of Incarceration and Health Outcomes Among Older Adults
Kenzie Latham-Mintus, Monica M Deck, Elizabeth Nelson, Jessica Kelley
The Journals of Gerontology: Series B.2023; 78(5): 853. CrossRef - The inverse U-shaped relationship between challenge stressors and workplace learning outcomes: a study of young employees in Japan
Megumi Ikeda
Journal of Workplace Learning.2023; 35(4): 359. CrossRef - Investigation of Real Estate Tax Leakage Loss Rates with ANNs
Mehmet Yılmaz, Bülent Bostancı
Buildings.2023; 13(10): 2464. CrossRef - Do Mobile Mental Health Applications Increase Access to University Mental Health Supports? Lessons Learned During the COVID-19 Pandemic
Deborah Ann Cohen, Brittany P. Boyer, Laura Stevens, Katie McCormick, Erin Morpeth, Norian A. Caporale-Berkowitz, Chris Brownson, Stephen M. Strakowski
Journal of Technology in Human Services.2023; 41(4): 259. CrossRef - How do childhood abuse and neglect affect prosocial behavior? The mediating roles of different empathic components
Peiyi Chen, Qiaofen Zhang, Xiyuan Sun, Xiaoyang Ye, You Wang, Xueling Yang
Frontiers in Psychology.2023;[Epub] CrossRef - Genetic Risk Scores for the Determination of Type 2 Diabetes Mellitus (T2DM) in North India
Lisa Mitsuko Shitomi-Jones, Liz Akam, David Hunter, Puneetpal Singh, Sarabjit Mastana
International Journal of Environmental Research and Public Health.2023; 20(4): 3729. CrossRef - Association of Affiliate Stigma with Parenting Stress and Its Moderators among Caregivers of Children with Attention-Deficit/Hyperactivity Disorder
Pei-Yun Lin, Wen-Jiun Chou, Ray C. Hsiao, Tai-Ling Liu, Cheng-Fang Yen
International Journal of Environmental Research and Public Health.2023; 20(4): 3192. CrossRef - COVID-19 PANDEMİSİ SÜRECİNDE SAĞLIK PROFESYONELLERİNDE ÇALIŞAN SADAKATİNİ ETKİLEYEN ORGANİZASYONEL FAKTÖRLERİN İNCELENMESİ: BİR ÜNİVERSİTE HASTANESİ ÖRNEĞİ
Meltem SAYGILI, Miraç ATASEVEN, Büşranur YILDIRIM
Hacettepe Sağlık İdaresi Dergisi.2023; 26(4): 1069. CrossRef - Açıköğretim Sisteminde öğrenenlerin canlı derslere ilişkin görüşleri
Öznur ÖZTÜRK, Özlem ERORTA, Emel GÜLER, Yusuf Zafer Can UĞURHAN
Açıköğretim Uygulamaları ve Araştırmaları Dergisi.2023; 9(1): 337. CrossRef - Üniversite Öğrencilerinin Web3 Teknolojileri Farkındalığının Çeşitli Değişkenler Açısından İncelenmesi
Ahmet ÇELİK, Mutlu Tahsin ÜSTÜNDAĞ, Onur CERAN, Mevlüt UYSAL, Mustafa TANRIVERDİ, Zafer AYAZ
Türk Eğitim Bilimleri Dergisi.2023; 21(3): 1710. CrossRef - Monitoring chest compressions using finger photoplethysmography in out-of-hospital cardiac arrest
Jon Urteaga, Elisabete Aramendi, Andoni Elola, Mohamud R. Daya, Ahamed H. Idris
Biomedical Signal Processing and Control.2023; 86: 105144. CrossRef - Italian validation of the Clinical Outcomes in Routine Evaluation 10 (CORE-10): a short measure for routine outcome monitoring in clinical practice
Antonino La Tona, Sofia Tagini, Agostino Brugnera, Barbara Poletti, Edoardo Nicolò Aiello, Gianluca Lo Coco, Lidia Del Piccolo, Angelo Compare
Research in Psychotherapy: Psychopathology, Process and Outcome.2023;[Epub] CrossRef - The Vocal Priorities of College Students With and Without Self-Reported Voice Problems
McKenna Hooper, Brittany L. Perrine, Rachel L. Carroll
Journal of Voice.2023;[Epub] CrossRef - Assessment of Psychometric Properties of the Malay Version of the Brief Resilience Scale (BRS-M) among Non-Academic Staff Working from Home during COVID-19 in Malaysia
Zuraida Ahmad Sabki, Lee Hui Kim, Mahmoud Danaee, Ahmad Hatim Sulaiman, Khairul Arif Razali, Ong Hui Koh, Sharmilla Kanagasundram, Manveen Kaur, Fatin Liyana Azhar, Benedict Francis
Healthcare.2023; 11(8): 1146. CrossRef - Beyond the Clinic: Maximum Free-Living Stepping as a Potential Measure of Physical Performance
Craig Speirs, Mark D. Dunlop, Marc Roper, Malcolm Granat
Sensors.2023; 23(14): 6555. CrossRef - Cultural Values: Their Correlations with Attitudes and Behaviors towards Senior Citizens
P.C. Siah, X.H. Ong, S.H. Tan, S.M. Tan
Cultural-Historical Psychology.2023; 19(4): 100. CrossRef - The Moderating Role of Entrepreneurial Self-Efficacy and Locus of Control on the Effect of the University Environment and Program on Entrepreneurial Intention and Attitudes
Aigerim Sekerbayeva, Saltanat Tamenova, Bulent Tarman, Servet Demir, Uldana Baizyldayeva, Saule Yussupova
European Journal of Educational Research.2023; volume-12-(volume-12-): 1539. CrossRef - Psychometric testing of the 10-item perceived stress scale for Chinese nurses
Xiaoyu Du, Xiqin Liu, Yajun Zhao, Song Wang
BMC Nursing.2023;[Epub] CrossRef - Exploration and optimization of extraction, analysis and data normalization strategies for mass spectrometry-based DNA adductome mapping and modeling
Marilyn De Graeve, Emma Van de Walle, Thomas Van Hecke, Stefaan De Smet, Lynn Vanhaecke, Lieselot Y. Hemeryck
Analytica Chimica Acta.2023; 1274: 341578. CrossRef - Modernization, collectivism, and gender equality predict love experiences in 45 countries
Piotr Sorokowski, Marta Kowal, Robert J. Sternberg, Toivo Aavik, Grace Akello, Mohammad Madallh Alhabahba, Charlotte Alm, Naumana Amjad, Afifa Anjum, Kelly Asao, Chiemezie S. Atama, Derya Atamtürk Duyar, Richard Ayebare, Daniel Conroy-Beam, Mons Bendixen,
Scientific Reports.2023;[Epub] CrossRef - Development and psychometric evaluation of an occupational health and safety performance tool for manufacturing companies
Abolfazl Ghahramani, Mahboub Ebrahimi, Mohammad Hajaghazadeh
Heliyon.2023; 9(6): e17343. CrossRef - Impact of Sodium Hypochlorite Applied as Nutrient Solution Disinfectant on Growth, Nutritional Status, Yield, and Consumer Safety of Tomato (Solanum lycopersicum L.) Fruit Produced in a Soilless Cultivation
Maira Lykogianni, Eleftheria Bempelou, Ioannis Karavidas, Christos Anagnostopoulos, Konstantinos A. Aliferis, Dimitrios Savvas
Horticulturae.2023; 9(3): 352. CrossRef - Diagnostic properties of the Italian ECAS Carer Interview (ECAS-CI)
Barbara Poletti, Edoardo Nicolò Aiello, Federica Solca, Silvia Torre, Laura Carelli, Roberta Ferrucci, Federico Verde, Nicola Ticozzi, Vincenzo Silani
Neurological Sciences.2023; 44(3): 941. CrossRef - Modeling Bankfull Channel Geometry Based on Watershed and Precipitation Characteristics Using Dimensionless Parameters
Hridaya Bastola, Panayiotis Diplas
Water Resources Research.2023;[Epub] CrossRef - From transgressors to authors: promoting EFL writing through academic integrity integrated instruction
Özgür Çelik, Salim Razı
System.2023; 117: 103101. CrossRef - Factors determining antenatal care utilization among mothers of deceased perinates in Ethiopia
Neamin Tesfay, Mandefro Kebede, Negga Asamene, Muse Tadesse, Dumesa Begna, Fitsum Woldeyohannes
Frontiers in Medicine.2023;[Epub] CrossRef - Cloud adoption in Indian SMEs – an empirical analysis
Jayalaxmi Padmanabha Shetty, Rajesh Panda
Benchmarking: An International Journal.2023; 30(4): 1345. CrossRef - After one year in university; a robust decrease in autistic traits reporting among autistic students
Gil Zukerman, Gili Yahav, Ester Ben-Itzchak
Frontiers in Psychiatry.2023;[Epub] CrossRef - Variables that influence teachers’ practice of differentiated instruction in Chinese classrooms: A study from teachers’ perspectives
Meijie Bi, Katrien Struyven, Chang Zhu
Frontiers in Psychology.2023;[Epub] CrossRef - Untroubled pullers: An examination of nonclinical hair-pulling
Meghan K. Flannery, Martha J. Falkenstein, Megan Boyd, David A.F. Haaga
Journal of Obsessive-Compulsive and Related Disorders.2023; 38: 100821. CrossRef - The effect of childhood trauma on suicide risk: the chain mediating effects of resilience and mental distress
Kaimin Yao, Peiyi Chen, Hui Zhou, Jiajia Ruan, Dan Chen, Xueling Yang, You Zhou
BMC Psychiatry.2023;[Epub] CrossRef - Green HRM, green innovation and environmental performance: The moderating role of servant leadership
Ella Mittal, Parvinder Kaur
Human Systems Management.2023; 42(1): 27. CrossRef - Relationship Between FoMO, Problematic Social Media Use, Self-esteem, Negative Affectivity, and Physical Exercise: A Structural Equation Model
Anastasios Dadiotis, Petros Roussos
Journal of Technology in Behavioral Science.2023; 9(2): 313. CrossRef - Are Demographic Characteristics Able to Predict Risky Behaviors of Pedestrians?
Anahita Abbaspour, Khadijeh Hajimiri, Shirazeh Arghami
Journal of Human Environment and Health Promotion.2023; 9(1): 47. CrossRef - Synergistic Interactions of Insufficient Physical Activity and a High Systemic Immune-Inflammation Index on Psychological Problems in Indonesians With Type 2 Diabetes Mellitus
Yohanes Andy Rias, Hsiu Ting Tsai, Ratsiri Thato, Bagus Sholeh Apriyanto, Kuei Ru Chou, Shu Chuan Ho, Chia Hsuan Sun
Biological Research For Nursing.2023; 25(4): 516. CrossRef - XFilter: An Extension of the Integrity Measurement Architecture Based on Fine-Grained Policies
Alan Litchfield, Weihua Du
Applied Sciences.2023; 13(10): 6046. CrossRef - Examining the Role of Student Responsiveness in Treatment Effects of a Tier 2 Program Targeting Reductions in Problem Behavior
Kevin S. Sutherland, Kristen Granger, Maureen A. Conroy, Bryce D. McLeod, Michael Broda, Natalie Vallarta, Albert Rosas
Prevention Science.2023; 24(5): 974. CrossRef - Cognitive function in recovered COVID-19 Lebanese patients with schizophrenia
Chadia Haddad, Angela Chamoun, Hala Sacre, Souheil Hallit, Pascale Salameh, Benjamin Calvet
Annals of General Psychiatry.2023;[Epub] CrossRef - Self-Reports Do Not Tell the Whole Story: A Study of Candidates for Bariatric Surgery Using A Multimethod Approach
Maíra Stivaleti Colombarolli, Luciano Giromini, Sonia Regina Pasian
Psychological Injury and Law.2023; 16(3): 249. CrossRef - A retrospective examination of changes in drinking motives during the early COVID-19 pandemic
Nichea S. Spillane, Melissa R. Schick, Tessa Nalven, Michael C. Crawford, Anika S. Martz
The International Journal of Psychiatry in Medicine.2023; 58(2): 102. CrossRef - Geochemistry and contamination of sediments and water in rivers affected by the rupture of tailings dams (Brumadinho, Brazil)
Fernando António Leal Pacheco, Renato Farias do Valle Junior, Maytê Maria Abreu Pires de Melo Silva, Teresa Cristina Tarlé Pissarra, Glauco de Souza Rolim, Marília Carvalho de Melo, Carlos Alberto Valera, João Paulo Moura, Luís Filipe Sanches Fernandes
Applied Geochemistry.2023; 152: 105644. CrossRef - Faster Walking Speeds Require Greater Activity from the Primary Motor Cortex in Older Adults Compared to Younger Adults
Lisa Alcock, Rodrigo Vitório, Samuel Stuart, Lynn Rochester, Annette Pantall
Sensors.2023; 23(15): 6921. CrossRef - Examining the Factors Related to the Technological Pedagogical and Content Knowledge Levels of Preservice Social Studies Teachers
Alpay Aksin
Sage Open.2023;[Epub] CrossRef - Income and Oral and General Health-Related Quality of Life: The Modifying Effect of Sense of Coherence, Findings of a Cross-Sectional Study
Mehrsa Zakershahrak, Sergio Chrisopoulos, Liana Luzzi, Lisa Jamieson, David Brennan
Applied Research in Quality of Life.2023; 18(5): 2561. CrossRef - Exploring the impact of envy and admiration on social media fatigue: Social media loneliness and anxiety as mediators
Qiang Yan, Yepeng Chen, Yuxian Jiang, Hejie Chen
Current Psychology.2023; 42(20): 16830. CrossRef - Exploring and Deepening the Facets of Mentalizing: The Integration of Network and Factorial Analysis Approaches to Verify the Psychometric Properties of the Multidimensional Mentalizing Questionnaire (MMQ)
Alessio Gori, Eleonora Topino
International Journal of Environmental Research and Public Health.2023; 20(6): 4744. CrossRef - İlişkisel Pazarlama Kapsamında Freelance Çalışanların Müşteri İlişkilerinin Çalışma Performanslarına Etkisi
Emine Pınar SAYGIN, Gökmen ÖNAL
Kahramanmaraş Sütçü İmam Üniversitesi Sosyal Bilimler Dergisi.2023; 20(2): 683. CrossRef - Family Experiences and Feedback: An Examination of Attrition in Parent-Child Interaction Therapy
Brittany K. Liebsack, Amy D. Herschell, Jonathan A. Hart, David J. Kolko, Carrie B. Jackson
Evidence-Based Practice in Child and Adolescent Mental Health.2023; 8(1): 10. CrossRef - Do proactive students benefit more from university support for entrepreneurship when it comes to choosing entrepreneurship as a career choice? An examination of Ghanian and Malaysian students
Michael J. Mustafa, Jia Wei Chin, Melati Nungsari, Kwami Justina Morris
The International Journal of Management Education.2023; 21(3): 100868. CrossRef - Feasibility of implementing patient-reported outcome measures into routine breast cancer care delivery using a novel collection and reporting platform
Elena Tsangaris, Colby Hyland, George Liang, Joanna O’Gorman, Dany Thorpe Huerta, Ellen Kim, Maria Edelen, Andrea Pusic
JAMIA Open.2023;[Epub] CrossRef - Probabilistic Assessment of Conservation Voltage Reduction Using Static Load Model Parameter in the Presence of Uncertainties
Mir Toufikur Rahman, Kazi N. Hasan, Peter Sokolowski, Hazlie Mokhlis
IEEE Transactions on Industry Applications.2023; 59(3): 2675. CrossRef - TURKISH ADAPTATION OF THE PROSOCIAL ORGANIZATIONAL BEHAVIORS SCALE: A VALIDITY AND RELIABILITY STUDY
Dilara Altunok, Faruk Kerem Şentürk
Elektronik Sosyal Bilimler Dergisi.2023; 22(85): 118. CrossRef - The pharmacokinetics of 38% silver diamine fluoride in healthy children with dental caries: a quasi-experimental study
S. P. Lim, N. Zainal Aalam, Z. Chik, S. Musa
European Archives of Paediatric Dentistry.2023; 24(6): 737. CrossRef - Real-World Intake of Dietary Sugars Is Associated with Reduced Cortisol Reactivity Following an Acute Physiological Stressor
Nicola Di Polito, Anthea A. Stylianakis, Rick Richardson, Kathryn D. Baker
Nutrients.2023; 15(1): 209. CrossRef - Breastfeeding and the quality of the sibling relationship
Gemma López-Fernández, Maite Barrios, Juana Gómez-Benito
Midwifery.2023; 125: 103778. CrossRef - The effect of customer incivility on employees' work effort and intention to quit: Mediating role of job satisfaction
Ali Doğantekin, Erhan Boğan, Bekir Bora Dedeoğlu
Tourism Management Perspectives.2023; 45: 101071. CrossRef - Relationship between stair ascent gait speed, bone density and gait characteristics of postmenopausal women
Ali Dostan, Catherine A. Dobson, Natalie Vanicek, John Leicester Williams
PLOS ONE.2023; 18(3): e0283333. CrossRef - Measuring loneliness: Psychometric properties of the three-item loneliness scale among community-dwelling adults
Fernanda Daniel, Helena Espírito-Santo, Laura Lemos, Sónia Guadalupe, Isabel Barroso, Alexandre Gomes da Silva, Pedro Lopes Ferreira
Heliyon.2023; 9(5): e15948. CrossRef - Impact of public service motivation on work evaluation and counterproductive work behaviour
Phakane M. Masukela, Petronella Jonck, Petrus A. Botha
SA Journal of Human Resource Management.2023;[Epub] CrossRef - Phase I test development for a brief assessment of transactional success in aphasia: methods and preliminary findings of main concepts in non-aphasic participants
Jacquie Kurland, Anna Liu, Polly Stokes
Aphasiology.2023; 37(1): 39. CrossRef - Relationship between emotional intelligence and learning motivation among college students during the COVID-19 pandemic: A serial mediation model
Yuxi Tang, Weiguang He
Frontiers in Psychology.2023;[Epub] CrossRef - The Impact of Executive Green Incentives and Top Management Team Characteristics on Corporate Value in China: The Mediating Role of Environment, Social and Government Performance
Yujuan Wu, Jacquline Tham
Sustainability.2023; 15(16): 12518. CrossRef - Canopy reflectance spectra’s variability, physical traits’ uniqueness and the prediction of rubber clones (Hevea brasiliensis)
Mohd Hafiz Mohd Hazir, Rashidi Daud, Muhamad Sufiy Shahabudin, Muhamad Faizal Othman, Nurmi Rohayu Abdul Hamid
Industrial Crops and Products.2023; 201: 116930. CrossRef - The Influence of Individual and Contextual Factors on the Vocational Choices of Adolescents and Their Impact on Well-Being
Stefania Fantinelli, Ciro Esposito, Leonardo Carlucci, Pierpaolo Limone, Francesco Sulla
Behavioral Sciences.2023; 13(3): 233. CrossRef - Functional Recovery of COVID-19 Patients Admitted to a Cardiopulmonary Inpatient Rehabilitation Unit
Amy Comley Steele, Heather McKenna, Amy Teale
COVID.2023; 3(9): 1310. CrossRef - Trace element contamination in soils surrounding the open-cast coal mines of eastern Raniganj basin, India
Prasenjeet Chakraborty, David A. Wood, Siddharth Singh, Bodhisatwa Hazra
Environmental Geochemistry and Health.2023; 45(10): 7275. CrossRef - Linking authentic leadership and employee turnover intention: the influences of sense of calling and job satisfaction
Ziyu Liu, Hung Wong
Leadership & Organization Development Journal.2023; 44(5): 585. CrossRef - Challenging behaviors among students with severe developmental disabilities in Saudi Arabia: Impact of socio-demographic differences
Rashed Aldabas
International Journal of Developmental Disabilities.2023; 69(2): 304. CrossRef - An intergroup contact approach for understanding attitudes and behaviours towards deaf students among hearing students in Malaysia
Poh Chua Siah, Chee Seng Tan, Wan Ying Lee, Mah Ngee Lee
Equality, Diversity and Inclusion: An International Journal.2023; 42(7): 927. CrossRef - Adolescents’ Out-of-School Physical Activity Levels and Well-Being during the COVID-19 Restrictions in Greece: A Longitudinal Study
Alexandros Lazaridis, Ioannis Syrmpas, Themistoklis Tsatalas, Charalampos Krommidas, Nikolaos Digelidis
Journal of Functional Morphology and Kinesiology.2023; 8(2): 55. CrossRef - Exploring the influence of tourists’ happiness on revisit intention in the context of Traditional Chinese Medicine cultural tourism
Jiamin Peng, Xiaoyun Yang, Senhui Fu, Tzung-Cheng (T.C.) Huan
Tourism Management.2023; 94: 104647. CrossRef - The relationship between reading skills and fine motor abilities in younger school-age children
Nataša Buha, Slobodan Banković, Milica Gligorović
Specijalna edukacija i rehabilitacija.2023; 22(2): 149. CrossRef - Writing Quality Predictive Modeling: Integrating Register-Related Factors
Heqiao Wang, Gary A. Troia
Written Communication.2023; 40(4): 1070. CrossRef - Financial Literacy of Workers in the Tourism Industry in Mexico in 2023: a Structural Equations Approach
Arturo García-Santillán, Francisco Venegas-Martínez, Ricardo Jacob Mendoza-Rivera
Revista Mexicana de Economía y Finanzas.2023; 19(1): 1. CrossRef - The links between grammar learning strategies and language mindsets among L2 and L3 learners: examining the role of gender
Nourollah Zarrinabadi, Mohsen Rezazadeh, Abdollah Chehrazi
International Journal of Multilingualism.2023; 20(2): 347. CrossRef - The impact of social capital on the resilience of flood-prone communities: The case study of northern Iran
Mousa Pazhuhan (Panahandeh Khah), Melika Amirzadeh, Rando Värnik, Marcin Pietrzykowski, David Lopez-Carr, Hossein Azadi
Environmental Development.2023; 48: 100902. CrossRef - Construction and validation of a questionnaire to study engagement in informal second language learning
Henriette L. Arndt
Studies in Second Language Acquisition.2023; 45(5): 1456. CrossRef - Reduction of drive for thinness and body dissatisfaction in people with self-reported dysregulated eating behaviors after intermittent theta burst stimulation (iTBS) of the left dorsolateral prefrontal cortex
Jennifer Barone, Massimiliamo Oliveri, Rosario Emanuele Bonaventura, Giuseppa Renata Mangano
Frontiers in Human Neuroscience.2023;[Epub] CrossRef - Impact of workplace safety on well-being: the mediating role of thriving at work
Norberth Okros, Delia Virga
Personnel Review.2023; 52(7): 1861. CrossRef - Mental well-being and test anxiety among students preparing for the university admission exam during the pandemic
Eleyza Yatkin, Neriman Aral, Lugen Ceren Gunes, Selim Tosun
Frontiers in Psychology.2023;[Epub] CrossRef - Cardiac Vagal Control Among Community Cigarette Smokers with Low to Moderate Depressive Symptoms
Hannah R. Brinkman, Danielle L. Hoyt, Erick J. Fedorenko, Wendy Berry Mendes, Teresa M. Leyro
Applied Psychophysiology and Biofeedback.2023; 48(2): 159. CrossRef - Definition and Criteria for the Assessment of Expertise in Psychotherapy: Development of the Psychotherapy Expertise Questionnaire (PEQ)
Alessio Gori, Eleonora Topino, Marco Cacioppo, Adriano Schimmenti, Vincenzo Caretti
European Journal of Investigation in Health, Psychology and Education.2023; 13(11): 2478. CrossRef - Enhancing meaningful work through meaning in life: Mediating effect of prosocial organizational and individual behaviors
Faruk Kerem ŞENTÜRK, Dilara ALTUNOK
Ege Akademik Bakis (Ege Academic Review).2023;[Epub] CrossRef - When Shooting for the Stars Becomes Aiming for Asterisks: P-Hacking in Family Business Research
Jasper Brinkerink
Entrepreneurship Theory and Practice.2023; 47(2): 304. CrossRef - Students’ Psychological Perceptions Toward Online Learning Engagement and Outcomes during the COVID-19 Pandemic: A Comparative Analysis of Students in Three Different Countries
Natalia Zapata-Cuervo, Maricela I. Montes-Guerra, Hyejo Hailey Shin, Miyoung Jeong, Mi-Hea Cho
Journal of Hospitality & Tourism Education.2023; 35(2): 108. CrossRef - Does workplace violence affect healthcare workers' turnover intention?
Leilei Liang, Zhi Wang, Yueyang Hu, Tongshuang Yuan, Junsong Fei, Songli Mei
Japan Journal of Nursing Science.2023;[Epub] CrossRef - Development and Psychometric Evaluation of the Ischemic Stroke Distress Scale (ISDS)
Jaejin Kang, Yang-Sook Yoo
Journal of Korean Academy of Nursing.2023; 53(1): 12. CrossRef - Development of a measure of kindness
Donna E. Youngs, Miroslava A. Yaneva, David V. Canter
Current Psychology.2023; 42(7): 5428. CrossRef - Studies of EEG Asymmetry and Depression: To Normalise or Not?
Christopher F. Sharpley, Wayne M. Arnold, Ian D. Evans, Vicki Bitsika, Emmanuel Jesulola, Linda L. Agnew
Symmetry.2023; 15(9): 1689. CrossRef - Evaluation of the Opinions of the Parents with Disabled and Healthy Children about Third Hand Smoke
Serkan Köksoy, Belkıs Can
Bağımlılık Dergisi.2023; 24(4): 487. CrossRef - The flipped classroom approach in an English for specific purposes (ESP) course: A quasi-experimental study on learners’ self-efficacy, study process, and learning performances
I-Chun Vera Hsiao, Shao-Ting Alan Hung, Heng-Tsung Danny Huang
Journal of Research on Technology in Education.2023; 55(3): 507. CrossRef - Adaptation of communication styles inventory to Russian context
Marina R. Zheltukhina, Natalia N. Kislitsyna, Olga V. Sergeeva, Roza M. Ignateva, Yuliya P. Kosheleva, Larisa Yu. Lutskovskaia
Contemporary Educational Technology.2023; 15(4): ep455. CrossRef - Effects of Cabri 3D Activities Blended into the 5E Model on Geometry Success
Burcu CEYLAN ELİYEŞİL, Gürkan TUNA
Abant İzzet Baysal Üniversitesi Eğitim Fakültesi Dergisi.2023; 23(4): 1987. CrossRef - Examining the influence of L2 grit and English proficiency on learning approaches: a mediation analysis through expectancy of success and perceived task difficulty
Mu-Hsuan Chou
Educational Psychology.2023; 43(9): 1102. CrossRef - Simulated window views from different building floors: How roof types of surrounding buildings associate with subjective restoration
Fei Wang, Jun Munakata
Urban Forestry & Urban Greening.2023; 89: 128096. CrossRef - Stature estimation by semi-automatic measurements of 3D CT images of the femur
Kei Kira, Fumiko Chiba, Yohsuke Makino, Suguru Torimitsu, Rutsuko Yamaguchi, Shigeki Tsuneya, Ayumi Motomura, Maiko Yoshida, Naoki Saitoh, Go Inokuchi, Yumi Hoshioka, Hisako Saitoh, Daisuke Yajima, Hirotaro Iwase
International Journal of Legal Medicine.2023; 137(2): 359. CrossRef - Prevalence and associated factors of alexithymia among people living with HIV/AIDS in China: a cross-sectional study
Huan Liu, Yisi Yang, Yingnan Tian, Shanshan Gao, Yunxia Ma, Yuxuan Wang, Ling Xin, Nana Luo, Xinyu Wang, Nan Meng, Ruiqian Zhuge, Qunkai Wang, Qunhong Wu, Baohua Liu
BMC Psychiatry.2023;[Epub] CrossRef - Examining environmentally responsible behaviour, environmental beliefs and conservation commitment of tourists: a path towards responsible consumption and production in tourism
Ataul Karim Patwary
Environmental Science and Pollution Research.2023; 30(3): 5815. CrossRef - Men’s Physical Attractiveness Predicts Women’s Ratings of Sexual Intent through Sexual Arousal: Implications for Sexual (Mis)Communication
Tyler N. Livingston, Peter O. Rerick
Sexes.2023; 4(3): 327. CrossRef - IS LEADERSHIP POSITION RELATED TO MORE SOCIAL INCLUSION, HAPPINESS, AND SATISFACTION WITH LIFE? THE IMPORTANCE OF POWER DISTANCE INDEX
Aurelija Stelmokienė, Gabija Jarašiūnaitė-Fedosejeva
Business: Theory and Practice.2023; 24(1): 148. CrossRef - Cumulative Risk and Mental Health of Left-behind Children in China: A Moderated Mediation Model
Junmei Xiong, Weiwei Xie, Tong Zhang
International Journal of Environmental Research and Public Health.2023; 20(2): 1105. CrossRef - Factors associated with perceived resilience among undergraduate nursing students: findings of the first cross-sectional study in Palestine
Aidah Alkaissi, Nizar B. Said, Shorooq Qadous, Mahdia Alkony, Omar Almahmoud
BMC Nursing.2023;[Epub] CrossRef - Attitudes toward pre-symptomatic screening for Alzheimer’s dementia in five European countries: a comparison of family members of people with Alzheimer’s dementia versus non-family members
Ioanna A. Angelidou, Marina Makri, Konrad Beyreuther, Mercè Boada Rovira, Akyllina Despoti, Sebastiaan Engelborghs, Andrea Miguel, Isabel Rodríguez, Hannah Stocker, Joke Temmerman, Magda Tsolaki, Görsev Yener, Deniz Yerlikaya, Birgit Teichmann
Frontiers in Genetics.2023;[Epub] CrossRef - Are Demographic Characteristics Able to Predict Risky Behaviors of Pedestrians?
Anahita Abbaspour, Khadijeh Hajimiri, Shirazeh Arghami
Journal of Human Environment and Health Promotion.2023; 9(1): 48. CrossRef - Construct Validity of the Autism Classification System of Functioning: Social Communication (ACSF:SC) Across Childhood and Adolescence
Diana Tajik-Parvinchi, Peter Rosenbaum, Mary Jo Cooley Hidecker, Eric Duku, Lonnie Zwaigenbaum, Caroline Roncadin, Stelios Georgiades, Stephen Gentles, Hanna Fang, Briano Di Rezze
Journal of Autism and Developmental Disorders.2023; 53(8): 3246. CrossRef - Relationship between Reaction Times and Post-COVID-19 Symptoms Assessed by a Web-Based Visual Detection Task
Natale Vincenzo Maiorana, Edoardo Nicolò Aiello, Barbara Poletti, Fabrizio Carusi, Angelica De Sandi, Matteo Guidetti, Roberto Prandin, Sara Marceglia, Nicola Ticozzi, Vincenzo Silani, Alberto Priori, Roberta Ferrucci
Healthcare.2023; 11(3): 284. CrossRef - Longitudinal associations between sleep and weight status in infants and toddlers
Agnes G. Bucko, Bridget Armstrong, Kerry L. McIver, Alexander C. McLain, Russell R. Pate
Pediatric Obesity.2023;[Epub] CrossRef - Emotional activation in video conferences equals that in in person meetings
Michelle Jerkku, Jonas Nordin, Niclas Kaiser
DIGITAL HEALTH.2023;[Epub] CrossRef - Gönüllü Çocuksuzluğa İlişkin Tutumların Çelişik Duygulu Cinsiyetçilik, Genel Muhafazakarlık ve Sosyal Onay İhtiyacı ile İlişkisi
Dilan YAR, Sinem ULAŞ, Yılmaz MUALLA
Uluslararası İnsan Çalışmaları Dergisi.2023; 6(11): 45. CrossRef - Cohesion and conflict for mothers during the pandemic: Results of the Portuguese version of the COVID‐19 Household Environment Scale
Joana Arsénio, Gabriela Fonseca, Alda Portugal, Carla Crespo
Family Process.2023; 62(4): 1592. CrossRef - The relationship between digital solution selling and value-based selling: a motivation-opportunity-ability (MOA) perspective
Paolo Guenzi, Edwin J. Nijssen
European Journal of Marketing.2023; 57(3): 745. CrossRef - Determinants of Technopreneurial Intention Among University Students: Individual Entrepreneurial Orientation (IEO) as Mediator
Wei-Loon Koe, Mohd Rusydi Abdul Rahim, Mohd Halim Mahphoth
Marketing and Management of Innovations.2023; 14(2): 185. CrossRef - Pandemi Döneminde Üniversite Öğrencilerinin İyilik Halleri
Fidan KORKUT OWEN, Deniz ALBAYRAK KAYMAK
Milli Eğitim Dergisi.2023; 52(240): 2441. CrossRef - Does older mean flexible? Psychological flexibility and illness cognitions in chronic medical conditions - the moderating effect of age
Gil Zukerman, Maya Maor, Tamar Reichard, Shulamit Ben-Itzhak
Psychology, Health & Medicine.2023; 28(7): 1844. CrossRef - Psychometric evaluation of the Chinese version of the Positive Health Behaviours Scale for clinical nurses: a cross-sectional translation
Linghui Kong, Tingting Lu, Chen Zheng, Huijun Zhang
BMC Nursing.2023;[Epub] CrossRef - Teacher Support and Chinese EFL Students’ Intention to Continue Online Learning: The Mediating Role of Negative Emotions
Yuanyuan Zuo
Modern English Education.2023; 24(1): 238. CrossRef - Resolving the complexity in Gen Z's envy occurrence: A cross‐cultural perspective
Nazan Colmekcioglu, Bekir Bora Dedeoglu, Fevzi Okumus
Psychology & Marketing.2023; 40(1): 48. CrossRef - The power of employee exchange belief: How psychological contract strength mediates the relationship of HR practice consistency and organizational commitment
Jin Feng Uen, Shu-Yuan Chen, David Ahlstrom, Meng-Chun Yang
Current Psychology.2023; 42(25): 21746. CrossRef - Association of loneliness with suicide risk and depression in individuals with schizophrenia: moderating effects of self-esteem and perceived support from families and friends
Yi-Lung Chen, Cian-Ruei Jian, Yu-Ping Chang, Shu-Ru Chao, Cheng-Fang Yen
Schizophrenia.2023;[Epub] CrossRef - Validation of the motion sickness severity scale: Secondary analysis of a randomized, double-blind, placebo-controlled study of a treatment for motion sickness
Mark É. Czeisler, Justina M. Pruski, Pan Wang, Jingyuan Wang, Changfu Xiao, Mihael H. Polymeropoulos, Vasilios M. Polymeropoulos, Alice Coles-Aldridge
PLOS ONE.2023; 18(1): e0280058. CrossRef - The effect of parenting styles on depressive symptoms among Chinese college students: The role of subjective well-being and Taq1A polymorphism
Yiqiu Hu, Zihao Zeng, Liyi Peng, Qin Yang
Current Psychology.2023; 42(23): 19573. CrossRef - Satisfaction and anxiety level during clinical training among nursing students
Faransa A. Ahmed, Nojoud Alrashidi, Rasha A. Mohamed, Abdulaziz Asiri, Amer Al Ali, Khaled H. Aly, Wael G. Nouh, Nehal A. Demerdash, Salwa Ali Marzouk, Ayat M. Omar, Marzouk M. Marzouk, Safa H. Alkalash, Shimaa M. Moursy, Doaa E. Fadila, Samar S. Eldin, A
BMC Nursing.2023;[Epub] CrossRef - The Impact of Chinese Primary School Teachers’ Sense of Work Meaningfulness on Organizational Commitment: A Chain Mediation Model
Sumei Yin, Xiangli Guan, Yaqi Zhang, Yang Li, Mary C Jobe, Md Zahir Ahmed
Psychology Research and Behavior Management.2023; Volume 16: 3477. CrossRef - Effect of cryotherapy on paclitaxel‐induced peripheral neuropathy of the hand in female breast cancer patients: A prospective self‐controlled study
Ting‐Ting Yang, Hsiang‐Chu Pai, Chiung‐Yao Chen
International Journal of Nursing Practice.2023;[Epub] CrossRef - Listen to the heart or mind first? Examining sequential coping mechanisms among Indians during the COVID-19 pandemic
Sanchita Srivastava, Puja Upadhaya, Renuka Jain
Frontiers in Psychology.2023;[Epub] CrossRef - Correlates of severity in a clinical staging model of schizophrenia: a cross-sectional study among 158 subjects
Fatima Hamieh, Souheil Hallit, Chadia Haddad, Sahar Obeid, Francois Kazour
BMC Psychiatry.2023;[Epub] CrossRef - Social media use and abuse: Different profiles of users and their associations with addictive behaviours
Deon Tullett-Prado, Vasileios Stavropoulos, Rapson Gomez, Jo Doley
Addictive Behaviors Reports.2023; 17: 100479. CrossRef - The chain mediating role of psychological resilience and neuroticism between intolerance of uncertainty and perceived stress among medical university students in Southwest China
Xiaoxiao Xu, Xiaofan Yan, Qianhui Zhang, Chen Xu, Min Li
BMC Psychiatry.2023;[Epub] CrossRef - The mediating role of openness to experience and curiosity in the relationship between mindfulness and meaning in life: evidence from four countries
Chee-Seng Tan, Intan Hashimah Mohd Hashim, Kai-Shuen Pheh, Chris Pratt, Min-Huey Chung, Anggi Setyowati
Current Psychology.2023; 42(1): 327. CrossRef - Exploring the factors influencing online civic engagement in a smart city: The mediating roles of ICT self-efficacy and commitment to community
Guosheng Deng, Shuo Fei
Computers in Human Behavior.2023; 143: 107682. CrossRef - Psychological distress and quality of life among Opioid Agonist Treatment service users with a history of injecting and non-injecting drug use: A cross-sectional study in Kathmandu, Nepal
Sagun Ballav Pant, Suraj Bahadur Thapa, John Howard, Saroj Prasad Ojha, Lars Lien, Eleni Petkari
PLOS ONE.2023; 18(2): e0281437. CrossRef - A Comparative Analysis of Management Education Quality of Public- and Private-funded Technology-enabled Learning Platforms in India
Priyadeep Dhouchak, Naresh Kumar
Global Business Review.2023;[Epub] CrossRef - Implementing Flanders System in the Quantification of the Emotional Aspects of Teacher-Student Discourse
Ilyes Gouider
SSRN Electronic Journal.2023;[Epub] CrossRef - The Relationship Between Teacher’s Autonomy-Supportive Behavior and Learning Strategies Applied by Students: The Role of Teacher Support and Equity
Agne Brandisauskiene, Loreta Buksnyte-Marmiene, Jurate Cesnaviciene, Gabija Jarasiunaite-Fedosejeva
Sage Open.2023;[Epub] CrossRef - Assessment of macronutrients status using digital soil mapping techniques: a case study in Maru’ak area in Lorestan Province, Iran
Anahid Salmanpour, Mohammad Jamshidi, Shahrokh Fatehi, Moradali Ghanbarpouri, Jahanbakhsh Mirzavand
Environmental Monitoring and Assessment.2023;[Epub] CrossRef - Young people’s perceptions of the challenges and opportunities during the Mainland China–Hong Kong convergence
T. Wing Lo, Gloria Hongyee Chan, Gabriel Kwun Wa Lee, Xin Guan, Sharon Ingrid Kwok
Humanities and Social Sciences Communications.2023;[Epub] CrossRef - Efficacy and mechanisms of 4-week MBSR on psychological distress in lung cancer patients: A single-center, single-blind, longitudinal, randomized controlled trial
Xu Tian, Zhongli Liao, Lijuan Yi, Ling Tang, Guihua Chen, María F. Jiménez Herrera
Asia-Pacific Journal of Oncology Nursing.2023; 10(1): 100151. CrossRef - How physical activity and passion color the passage of time: A response with ultra-trail runners
Quentin Hallez, Marine Paucsik, Guillaume Tachon, Rebecca Shankland, Fanny Marteau-Chasserieau, Mathilde Plard
Frontiers in Psychology.2023;[Epub] CrossRef - Higher Sedentary Behaviors and Lower Levels of Specific Knowledge Are Risk Factors for Physical Activity-Related Injuries in Saudi Adolescents
Mohamed Ahmed Said, Amnah Ahmed Almatar, Mohammed Shaab Alibrahim
International Journal of Environmental Research and Public Health.2023; 20(5): 4610. CrossRef - The boosting of the total quality management on corporate green growth in emerging markets: the mediating roles of corporate social responsibility and customer loyalty
Thanh Tiep Le
Benchmarking: An International Journal.2023; 30(9): 3554. CrossRef - Survey data assessing the junior high school students’ learning attitudes toward home-based education amidst the Covid-19 pandemic
Dr. Saniya G. Abirin
Data in Brief.2023; 48: 109241. CrossRef - The Relation Between Autism Spectrum Disorder Traits, Attention-Deficit/Hyperactivity Disorder Traits, and Emotional Problems in Japanese University Students
Aya Saito, Satoko Matsumoto, Yukina Sakata, Masumi Sugawara
Advances in Neurodevelopmental Disorders.2023; 7(4): 525. CrossRef - Effects of shift work schedules, compensatory sleep, and work–family conflict on fatigue of shift‐working nurses in Chinese intensive care units
Shanshan Chen, Huihui Wu, Mimi Sun, Qing Wei, Qixia Zhang
Nursing in Critical Care.2023; 28(6): 948. CrossRef - A validation of the Pseudoscience Endorsement Scale and assessment of the cognitive correlates of pseudoscientific beliefs
Marta N. Torres, Itxaso Barberia, Javier Rodríguez-Ferreiro
Humanities and Social Sciences Communications.2023;[Epub] CrossRef - Lessons from the Pandemic: Analyzing the Experience of Distant Learning in Secondary Schools
E.A. Alenina, K.V. Bartseva, O.V. Lee, M.S. Zaleshin, M.V. Likhanov, Yu.V. Kovas
Psychological Science and Education.2023; 27(6): 84. CrossRef - Liver-X-receptor agonists rescue axonal degeneration in SPG11-deficient neurons via regulating cholesterol trafficking
Eric Chai, Zhenyu Chen, Yongchao Mou, Gitika Thakur, Weihai Zhan, Xue-Jun Li
Neurobiology of Disease.2023; 187: 106293. CrossRef - Academic distress among undergraduate students during COVID-19: the relevance of SES and help-seeking behaviors
Liat Korn, Avi Zigdon, Nitza Davidovitch
Frontiers in Psychology.2023;[Epub] CrossRef - There is more to attraction than meets the eye: Studying decoy‐induced attention allocation without eye tracking
Marco Marini, Alessandro Sapienza, Fabio Paglieri
Journal of Behavioral Decision Making.2023;[Epub] CrossRef - The influence of upright posture on craniospinal, arteriovenous, and abdominal pressures in a chronic ovine in-vivo trial
Anthony Podgoršak, Nina Eva Trimmel, Markus Florian Oertel, Margarete Arras, Miriam Weisskopf, Marianne Schmid Daners
Fluids and Barriers of the CNS.2023;[Epub] CrossRef - Effects of dietary synbiotics and biofloc meal on the growth, tissue histomorphology, whole-body composition and intestinal microbiota profile of Nile tilapia (Oreochromis niloticus) cultured at different salinities
Mursal Abdulkadir Hersi, Ercument Genc, Atakan Pipilos, Emre Keskin
Aquaculture.2023; 570: 739391. CrossRef - The Mediating Role of Procrastination in the Relationship between Fear of Missing Out and Internet Addiction in University Students
Abdullah Manap, Amelia Rizzo, Abdullah Yıldırmaz, Ümit Dilekçi, Murat Yıldırım
International Journal of Environmental Research and Public Health.2023; 21(1): 49. CrossRef - The involvement of inhibition in word and sentence reading
Margot De Rom, Arnaud Szmalec, Marie Van Reybroeck
Reading and Writing.2023; 36(5): 1283. CrossRef - Professional Identity of Medical Students of Malaysia: Influence of Demographic Factors
Ashok Kumar Jeppu, S.M. Ferdous Azam, Kavitha Ashok Kumar
Malaysian Journal of Medicine and Health Sciences.2023; 19(3): 196. CrossRef - A hybrid scoring system for prioritization of software vulnerabilities
Abhishek Sharma, Sangeeta Sabharwal, Sushama Nagpal
Computers & Security.2023; 129: 103256. CrossRef - Pain-Related Anxiety in Spanish-Speaking Mexican Americans Who Report Chronic Pain: Psychometric Evaluation of a New Spanish Adaptation of the 20-Item Pain Anxiety Symptom Scale (PASS-20)
Cristian Garcia-Alcaraz, Scott C. Roesch, Rosa Cobian Aguilar, Sara Gombatto, Kristen J. Wells
The Journal of Pain.2023; 24(8): 1434. CrossRef - An integrated perspective of the demand–control and effort–reward imbalance models on burnout among sport coaches: The moderating role of over-commitment and coaching efficacy
Changliang Yan, Dojin Jang, Sungho Kwon, Qingyun Jin
International Journal of Sports Science & Coaching.2023; 18(6): 1929. CrossRef - Mindfulness and Imagery Enhanced Behavioral Parenting: Effectiveness Pilot of the Confident Carers Cooperative Kids Program
Mark O. Donovan, Kathryn Briscoe-Hough, Emma Barkus, Jane S. Herbert, Leonie Miller, Greg Konza, Judy A. Pickard
Journal of Child and Family Studies.2023; 32(5): 1504. CrossRef - How Motivation and Digital Affordances Shape User Behavior in a Virtual World
Joomi Lee, Allison Eden
Media Psychology.2023; 26(5): 551. CrossRef - Mediating factors explain anxiety experienced by women with obesity during the Covid-19 pandemic
Isabel Urdapilleta, Lionel El Khoury, Jean-Marc Catheline, Saadi Lahlou, Samuel Demarchi, Ali B. Mahmoud
PLOS ONE.2023; 18(12): e0295034. CrossRef - The Impact of Autonomous and Controlled Sexting Motivations on Subjective Well-being and Relationship Quality
Lily Le, Lauren D. Goegan, Lia M. Daniels
Archives of Sexual Behavior.2023; 52(1): 243. CrossRef - Psychometric Evaluation of the Bangla Version of the Self-Compassion Scale-Short Form (SCS-SF)
Md. Musfikur Rahman, Md. Monimul Huq, Shadman Shakib, Mohd. Ashik Shahrier
Mindfulness.2023; 14(11): 2795. CrossRef - Professional engagement and professional values among teachers in Turkish primary schools: Examining the mediating effect of professional efficacy
Betül Balkar, Sedat Alev
Psychology in the Schools.2023; 60(3): 638. CrossRef - The role of culture in the association between racial discrimination and alcohol use among North American Indigenous adolescents reporting recent drinking
Melissa R. Schick, Tessa Nalven, Alana Egan, Nichea S. Spillane
Alcohol: Clinical and Experimental Research.2023; 47(6): 1109. CrossRef - An extended theory of planned behavior to explain the intention to use carsharing: a multi-group analysis of different sociodemographic characteristics
Leiming Li, Yu Zhang
Transportation.2023; 50(1): 143. CrossRef - Metacognitive Awareness and the Hot Hand: When Winning, No Amount of Awareness Will Have Strong Believers Avoid the Heuristic
Yeonho Choi, Lisa K. Son
Journal of Intelligence.2023; 11(7): 149. CrossRef - Implicit and explicit racial prejudice and stereotyping toward Black (vs. White) Americans: The prevalence and variation among genetic counselors in North America
Nao Hagiwara, Conor Duffy, John Quillin
Journal of Genetic Counseling.2023; 32(2): 397. CrossRef - The effect of covert narcissism on workplace incivility: The mediating role of self-esteem and norms for respect
Chanki Moon, Catarina Morais
Current Psychology.2023; 42(21): 18108. CrossRef - Relationship between gender equality, employees‘ perception of distributive justice and wellbeing in EU: The effect of gender and management position
Aurelija Stelmokienė, Gabija Jarašiūnaitė-Fedosejeva, Karina Kravčenko
Economics & Sociology.2023; 16(1): 138. CrossRef - Self-Transcendent Positive Emotions as a Potential Mechanism Underpinning the Effects of Meaningful Psychedelic Experiences on Connectedness to Nature
Katie Newton, Sam G. Moreton
Ecopsychology.2023; 15(2): 142. CrossRef - Emotional eating – A response to or one of the causes of paranoia-like thoughts? The bidirectional mediating role of avoidant coping
Paulina Bagrowska, Łukasz Gawęda
Psychiatry Research Communications.2023; 3(4): 100141. CrossRef - Development and Validation of the Gay-Specific Intraminority Stigma Inventory (G-SISI): Initial Evidence Underpinned by Intraminority Stress Theory
Benjamin F. Shepherd, Justin L. Maki, David G. Zelaya, Şeniz Warner, Adriana Wilson, Paula M. Brochu
European Journal of Investigation in Health, Psychology and Education.2023; 13(1): 170. CrossRef - Do the innovation and digital transformation strategies induce sme performances In new normal era? Structrual & confirmatory analysis models
Hosam Azat Elsaman, Tamadher Aldabbagh, Dina Sabry Said, Suriya Kumaran Kousihan, Genaro V. Japos
Acta Innovations.2023; (47): 41. CrossRef - Provisional drivers intend to speed less: The positive outcome for young drivers of a safe-driving app randomised trial
Daniel Vankov, Ronald Schroeter, Andry Rakotonirainy
Transportation Research Interdisciplinary Perspectives.2023; 21: 100877. CrossRef - Translation and Validation of the German Personal Growth Initiative Scale – II
Arne Weigold, Ingrid K. Weigold, Emily T. Ethridge, Yun Kai Chong
The Counseling Psychologist.2023; 51(7): 906. CrossRef - Psikolojik Güçlendirme Yaklaşımı ile Öğretmenlerin Proaktif Davranış Düzeyleri Arasındaki İlişkinin İncelenmesi
Selçuk DEMİR
Abant İzzet Baysal Üniversitesi Eğitim Fakültesi Dergisi.2023; 23(2): 839. CrossRef - Enhancing reading capability of young Thai students with augmented reality technology: Design-based research
Jaitip Nasongkhla, Siridej Sujiva
Contemporary Educational Technology.2023; 15(1): ep403. CrossRef - Examining the impact of perceived psychological distances of quitting and continuing tobacco smoking on antismoking intention: a cross-sectional study
Domonkos File, Beáta Bőthe, Zsolt Demetrovics
Scientific Reports.2023;[Epub] CrossRef - A 3-year longitudinal investigation of the overlap and stability of English and French word reading difficulties in French immersion children
Sharry Shakory, Klaudia Krenca, Stefka H. Marinova-Todd, Xi Chen
Annals of Dyslexia.2023; 73(1): 53. CrossRef - The Nepean Belief Scale (NBS) as a tool to investigate the intensity of beliefs in anorexia nervosa: psychometric properties of the Italian version
Arianna Sciarrillo, Francesco Bevione, Marta Lepora, Federica Toppino, Maria Carla Lacidogna, Nadia Delsedime, Matteo Panero, Matteo Martini, Giovanni Abbate Daga, Antonio Preti
Eating and Weight Disorders - Studies on Anorexia, Bulimia and Obesity.2023;[Epub] CrossRef - Comorbidity burden and health-related quality of life in men with advanced prostate cancer
Roberto M. Benzo, Patricia I. Moreno, Rina S. Fox, Carlos A. Silvera, Emily A. Walsh, Betina Yanez, Raymond R. Balise, Laura B. Oswald, Frank J. Penedo
Supportive Care in Cancer.2023;[Epub] CrossRef - Self-directed learning skills and motivation during distance learning in the COVID-19 pandemic (case study: The university of Jordan)
Laith M. Almomani, Niveen Halalsheh, Hanadi Al-Dreabi, Leena Al-Hyari, Raed Al-Quraan
Heliyon.2023; 9(9): e20018. CrossRef - Teacher-student relationships and smartphone addiction: the roles of achievement goal orientation and psychological resilience
Zifu Shi, Jinliang Guan, Huohong Chen, Chengzhen Liu, Jing Ma, Zhihao Zhou
Current Psychology.2023; 42(20): 17074. CrossRef - Investigating the Impacts of Adolescents’ Computer and Internet Use on Their Social Anxiety and Peer Relationships
Aleyna Yalçınkaya, Rahime İmamoğlu, Ece Tecim, Hilal Uymaz, Ebru Uysal, Lügen Ceren Güneş, Neriman Aral, Selim Tosun
Turkish Journal of Child and Adolescent Mental Health.2023; 30(3): 206. CrossRef - Mediating effect of resilience on the relationship between perceived social support and burnout among Chinese palliative nurses
Yalin Zhang, Chang Guan, Jianjun Jiang, Chuanmei Zhu, Xiaolin Hu
Journal of Clinical Nursing.2023; 32(13-14): 3887. CrossRef - Plasma metabolomic profiles associated with mortality and longevity in a prospective analysis of 13,512 individuals
Fenglei Wang, Anne-Julie Tessier, Liming Liang, Clemens Wittenbecher, Danielle E. Haslam, Gonzalo Fernández-Duval, A. Heather Eliassen, Kathryn M. Rexrode, Deirdre K. Tobias, Jun Li, Oana Zeleznik, Francine Grodstein, Miguel A. Martínez-González, Jordi Sa
Nature Communications.2023;[Epub] CrossRef - Quality of energy intake in Malaysian adolescents: prevalence, characteristics, determinants and impact of implausible reporters
Mohamed S Zulfarina, Razinah Sharif, Ahmad Mohd Sharkawi, Sabarul Afian Mokhtar, Ahmad Nazrun Shuid, Isa Naina-Mohamed
Public Health Nutrition.2023; 26(1): 122. CrossRef - Alexithymia and Fetal Attachment in Expectant Fathers
Duygu GÜLEÇ ŞATIR, Oya KAVLAK
Artuklu International Journal of Health Sciences.2023; 3(2): 123. CrossRef - Using a Back Exoskeleton During Industrial and Functional Tasks—Effects on Muscle Activity, Posture, Performance, Usability, and Wearer Discomfort in a Laboratory Trial
Tessy Luger, Mona Bär, Robert Seibt, Monika A. Rieger, Benjamin Steinhilber
Human Factors: The Journal of the Human Factors and Ergonomics Society.2023; 65(1): 5. CrossRef - PSİKOLOJİK SAĞLAMLIĞIN PSİKİYATRİK SEMPTOMLAR SAĞLIK KAYGISI VE SİBERKONDRİA İLİŞKİSİNDE ARACILIK ROLÜNÜN İNCELENMESİ
Duygu Yücel, Hilal Aslan, Osman Arıcak
İnönü Üniversitesi Sağlık Hizmetleri Meslek Yüksek Okulu Dergisi.2023; 11(3): 1684. CrossRef - The perception of affective touch in women affected by obesity
Sofia Tagini, Massimo Scacchi, Alessandro Mauro, Federica Scarpina
Frontiers in Psychology.2023;[Epub] CrossRef - Bullying in professional sports: psychological needs of athletes
Shi Y. JIE
The Journal of Sports Medicine and Physical Fitness.2023;[Epub] CrossRef - A novel 3D printed personalised insole for improvement of flat foot arch compression and recoil – preliminary study
Che-Wei Hu, Canh Toan Nguyen, Dominik Hölbling, Toh Yen Pang, Arnold Baca, Peter Dabnichki
Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications.2023; 237(2): 329. CrossRef - The digital skills divide: evidence from the European tourism industry
Sheena Carlisle, Stanislav Ivanov, Corné Dijkmans
Journal of Tourism Futures.2023; 9(2): 240. CrossRef - Is Endocervical Glandular Involvement Related to The Depth of Cone Biopsy?
Serkan Akis, Esra Keles, Sefik Eser Ozyurek, Yunus Emre Purut, Ugur Kemal Ozturk, Canan Kabaca, Murat Api, Handan Cetiner
International Journal of Surgical Pathology.2023; 31(1): 11. CrossRef - Predicting formative feedback practices: improving learning and minimising a tendency to ignore feedback
Gavin T. L. Brown, Catarina Andersson, Mikael Winberg, Torulf Palm
Frontiers in Education.2023;[Epub] CrossRef - Accuracy and Bias in Facial Trustworthiness Appraisals in Borderline Personality Disorder
Annemarie Miano, Sophia Lustig, Luca Meyerding, Sven Barnow
Journal of Personality Disorders.2023; 37(5): 525. CrossRef - Press Play to Feel: The Role of Attachment Styles and Alexithymic Features in Problematic Gaming
Andrea Scalone, Gianluca Santoro, Josephin Cavallo, Alessandra Melita, Alessio Gori, Adriano Schimmenti
International Journal of Environmental Research and Public Health.2023; 20(20): 6910. CrossRef - Online Game Speculative Experiences and Problem Gambling among Adolescents in South Korea: Dual Mediation Effects of Irrational Beliefs and Gambling Attitude
Jae-Kyoung Lee, Soo-Bi Lee
Healthcare.2023; 11(9): 1226. CrossRef - Goal Orientation and Adolescent Social Competence: Ubuntu as a Mediator Among Black American Adolescents
Husain Lateef, Dominique Horton, Laura Brugger, Mansoo Yu, Francine C. Jellesma, Baffour Boaten Boahen-Boaten, Ellie Borgstrom
Journal of Prevention.2023; 44(3): 325. CrossRef - Effects of Lentil Flour on the Quality of Gluten-free Muffins
Meltem Ece GÜLHAN, Aslı CAN KARAÇA
Deu Muhendislik Fakultesi Fen ve Muhendislik.2023; 25(74): 287. CrossRef - Psychometric validation of the Chinese version of the desire thinking questionnaire in adolescent mobile phone users
Lingfeng Gao, Xiaomin Wang, Gabriele Caselli, Weijian Li, Qingqi Liu, Xiaowei Chu, Haide Chen
Addictive Behaviors.2023; 142: 107651. CrossRef - Predictors of pretraumatic stress during the COVID-19 pandemic in Poland
Agnieszka E. Łyś, Mirosława Huflejt-Łukasik, Małgorzata Gambin, Anna Studzińska, Kamilla Bargiel-Matusiewicz, Tomasz Oleksy, Anna Wnuk, Daniel Pankowski, Sohaib Mustafa
PLOS ONE.2023; 18(8): e0290151. CrossRef - A longitudinal examination of school-related and mental health mediators linking emotion regulation to academic achievement
Tracy K.Y. Wong, Tyler Colasante, Tina Malti
Journal of School Psychology.2023; 101: 101253. CrossRef - Buckling behavior of Dendrocalamus sericeus Munro bamboo bars: Experiments and application
Worathep Sae-Long, Thanakorn Chompoorat, Suchart Limkatanyu, Chayanon Hansapinyo, Nattapong Damrongwiriyanupap, Piti Sukontasukkul, Tanan Chub-Uppakarn, Pannipa Chaowana
Journal of Building Engineering.2023; 80: 108027. CrossRef - Factors Related to Patients' Self-care and Self-care Confidence in Korean Patients With Heart Failure and Their Caregivers
Seongkum Heo, Mi-Seung Shin, Mee Ok Lee, Sangsuk Kim, Sun Hwa Kim, Justus Randolph, Se-Ran Jun, Minjeong An, Songthip Ounpraseuth, JinShil Kim
Journal of Cardiovascular Nursing.2023; 38(2): 140. CrossRef - Feasibility and diagnostics of the Frontal Assessment Battery (FAB) in amyotrophic lateral sclerosis
Edoardo Nicolò Aiello, Federica Solca, Silvia Torre, Laura Carelli, Roberta Ferrucci, Alberto Priori, Federico Verde, Nicola Ticozzi, Vincenzo Silani, Barbara Poletti
Neurological Sciences.2023; 44(2): 587. CrossRef - Multidecadal summer monsoon rainfall trend reversals in South Peninsular India: A new approach to examining long-term rainfall dataset
Swagatika Chakra, Akash Ganguly, Harsh Oza, Virendra Padhya, Amit Pandey, R.D. Deshpande
Journal of Hydrology.2023; 624: 129975. CrossRef - The combined impact of social networks and connectedness on anxiety, stress, and depression during COVID-19 quarantine: a retrospective observational study
Huiting Luo, Dan Luo, Qiao Tang, Zhiang Niu, Jiajun Xu, Jing Li
Frontiers in Public Health.2023;[Epub] CrossRef - Evaluation of uranium content and annual ingestion dose in the surface and ground water bodies of Chittorgarh, Rajasthan, India
Tejpal Menaria, Shailesh Nath Tiwari, Akshay Kumar Patra, Inampudi Vijaya Saradhi, A Vinod Kumar, Rama Kanwar Khangarot, Devendra Singh Rathore
Environmental Monitoring and Assessment.2023;[Epub] CrossRef - Childbirth fear in the USA during the COVID-19 pandemic: key predictors and associated birth outcomes
Z M Thayer, S A Geisel-Zamora, G Uwizeye, T E Gildner
Evolution, Medicine, and Public Health.2023; 11(1): 101. CrossRef - Rotational Set Up Uncertainly in Non-6D Couch and its Effects in Clinical Target Volume- Planning Target Volume Margin Calculation for Different Sites
Ngangom Robert, Tinish Sehgal, Ranjit Singh, Arun Oinam, Gaurav Trivedi, Budhi Singh, Amit Bahl, Renu Madan, Bhavana Rai
Journal of Medical Physics.2023; 48(1): 43. CrossRef - Exploring the Relations of Morphological Awareness with Phonological Awareness and Vocabulary: The Case of the Greek Language
Sophia Giazitzidou, Ioannis Grigorakis, Angeliki Mouzaki, Susana Padeliadu
Journal of Psycholinguistic Research.2023; 52(6): 2621. CrossRef - Assessment of diversity in anti-nutrient profile, resistant starch, minerals and carbohydrate components in different ricebean (Vigna umbellata) accessions
Paras Sharma, Giridhar Goudar, Anil Kumar Chandragiri, R. Ananthan, K. Subhash, Anitha Chauhan, T. Longvah, Mohar Singh, Rakesh Bhardwaj, Swarup Kumar Parida, Amit Kumar Singh, Gayacharan, Debasis Chattopadhyay
Food Chemistry.2023; 405: 134835. CrossRef - The role of parental rejection and poverty in the development of prosocial behavior among left-behind adolescents in rural China
Ling He, Chee-Seng Tan, Pit-Wan Pung, Jie Hu, Hai-Bo Tang, Siew-May Cheng
Children and Youth Services Review.2023; 155: 107143. CrossRef - The Association of Asthma with Anxiety, Depression, and Mild Cognitive Impairment among Middle-Aged and Elderly Individuals in Saudi Arabia
Sameera Abuaish, Huda Eltayeb, Asmatanzeem Bepari, Syed Arif Hussain, Raneem Saad Alqahtani, Waad Saeed Alshahrani, Amjad Hayf Alqahtani, Nada Saad Almegbil, Wafa Nedal Alzahrani
Behavioral Sciences.2023; 13(10): 842. CrossRef - There is more to cluttering than meets the eye: The prevalence of cluttering and association with psychological well‐being indices in an undergraduate sample
Michal Icht, Gil Zukerman, Avi Zigdon, Liat Korn
International Journal of Language & Communication Disorders.2023; 58(6): 2022. CrossRef - High-definition transcranial direct current stimulation (HD-tDCS) of the left middle temporal gyrus (LMTG) improves mathematical reasoning
Mengyi Li, Dazhi Cheng, Chuansheng Chen, Xinlin Zhou
Brain Topography.2023; 36(6): 890. CrossRef - Geochemical Modeling of Copper Mineralization Using Geostatistical and Machine Learning Algorithms in the Sahlabad Area, Iran
Aref Shirazi, Ardeshir Hezarkhani, Adel Shirazy, Amin Pour
Minerals.2023; 13(9): 1133. CrossRef - Investigating students’ attitudes towards translation technology: The status quo and structural relations with translation mindsets and future work self
Sha Tian, Lingxiao Jia, Zhining Zhang
Frontiers in Psychology.2023;[Epub] CrossRef - The effect of tourism live streaming information quality and source credibility on users’ continuous viewing intention: an application of elaboration likelihood model
Wenyuan Sang, Siyu Ji, Bo Pu, Ian Phau
Asia Pacific Journal of Tourism Research.2023; 28(3): 177. CrossRef - The effect of digital game-based learning on secondary level students’ learning of Internet literacy
Hakan Tüzün, Sedef Sert, Ömer Demir
Education and Information Technologies.2023; 28(7): 8837. CrossRef - An Examination of Cardiac Vagal Control Indices and Cognitive Stress Appraisal in Cigarette Smokers
Hannah R. Brinkman, Danielle E. McCarthy, Wendy B. Mendes, Teresa M. Leyro
Applied Psychophysiology and Biofeedback.2023; 48(1): 97. CrossRef - The State of Rest Break Practices Among 12-Hour Shift Hospital Nurses in the United States
Knar Sagherian, Hyeonmi Cho, Linsey M. Steege
JONA: The Journal of Nursing Administration.2023; 53(5): 277. CrossRef - The attitude of healthcare providers towards medication self‐management in hospitalized patients diagnosed with schizophrenia or bipolar disorders
Elke Loots, Tinne Dilles, Sarah Hadouchi, Bart Van Rompaey, Manuel Morrens
Journal of Psychiatric and Mental Health Nursing.2023; 30(4): 761. CrossRef - Frontal lobe-related cognition in the context of self-disgust
Vasileia Aristotelidou, Paul G. Overton, Ana B. Vivas, Alexandra Kavushansky
PLOS ONE.2023; 18(8): e0289948. CrossRef - Are tourists neophobic against offal meals?
Aliye Akin, Adnan Akin, Hakan Tahiri Mutlu
International Journal of Gastronomy and Food Science.2023; 31: 100684. CrossRef - Reliability and validity of the Turkish version of the teachers’ basic ICT competence beliefs scale
Pınar KORUKLUOĞLU, Bülent ALCI, Charlott RUBACH
International Journal of Assessment Tools in Education.2023; 10(1): 29. CrossRef - Examining the Effects of “Small Private Online Course and Flipped-Classroom”-Based Blended Teaching Strategy on First-Year English-Major Students’ Achievements
Luyan Zheng, Keok Cheong Lee
Sustainability.2023; 15(21): 15349. CrossRef - Assessing non‐right‐handedness and atypical cerebral lateralisation as predictors of paediatric mental health difficulties
Zubin A. Irani, Andrew M. C. Sheridan, Nicholas A. Badcock, Allison Fox
European Journal of Neuroscience.2023; 58(10): 4195. CrossRef - Transit Usage in Social Shocks: A Case Study of Station-Level Metro Ridership in Anti-Extradition Protests in Hong Kong
Ho-Yin Chan, Hanxi Ma, Jiangping Zhou
Transportation Research Record: Journal of the Transportation Research Board.2023; 2677(1): 1197. CrossRef - Investigating digital skills among Russian higher education students
Fatima K. Urakova, Izida I. Ishmuradova, Nataliia A. Kondakchian, Roza Sh. Akhmadieva, Julia V. Torkunova, Irina N. Meshkova, Nikolay A. Mashkin
Contemporary Educational Technology.2023; 15(1): ep398. CrossRef - Factors affecting domestic tourists’ repeat purchase intention towards accommodation in Malaysia
Charles Ramendran SPR, Hui Nee Au Yong, Maryam Kalhoro, Kamarulzaman Bin Mohd Dahari, Farhan Bashir Shaikh
Frontiers in Psychology.2023;[Epub] CrossRef - The Effect of Self-Investment on Hoarding Tendency of Chinese College Students: Role of Psychological Connections
Xiangli Guan, Yue Zhang, Yang Li, Yaqi Zhang, Jingjing Wang, Xuejiao Li, Mary C. Jobe, Md Zahir Ahmed, Oli Ahmed
International Journal of Mental Health Promotion.2023; 25(6): 755. CrossRef - Psychometrics and diagnostics of the Italian version of the Beck Depression Inventory-II (BDI-II) in Parkinson’s disease
Gianpaolo Maggi, Alfonsina D’Iorio, Edoardo Nicolò Aiello, Barbara Poletti, Nicola Ticozzi, Vincenzo Silani, Marianna Amboni, Carmine Vitale, Gabriella Santangelo
Neurological Sciences.2023; 44(5): 1607. CrossRef - Sense of Relational Entitlement and Couple Outcomes: The Mediating Role of Couple Negotiation Tactics
Octav-Sorin Candel
Behavioral Sciences.2023; 13(6): 467. CrossRef - Variations in Women’s Attribution of Blame for Sexual Assault
Sierra Strickler, Laura N. Martin, Kathleen Khong, Lauren Cattaneo
Journal of Interpersonal Violence.2023; 38(19-20): 10947. CrossRef - Enhancing spatial skills of young children with special needs using the Osmo Tangram based on tangible technology versus a Tangram card game
Orly Lahav, Ana Wolfson
Virtual Reality.2023; 27(1): 451. CrossRef - Clinimetrics of the Italian version of the Montreal Cognitive Assessment (MoCA) in adult-onset idiopathic focal dystonia
Alfonsina D’Iorio, Edoardo Nicolò Aiello, Assunta Trinchillo, Vincenzo Silani, Nicola Ticozzi, Andrea Ciammola, Barbara Poletti, Marcello Esposito, Gabriella Santangelo
Journal of Neural Transmission.2023; 130(12): 1571. CrossRef - The effect of research on the perceived quality of teaching: a cross-sectional study among university students in Lebanon
Hala Sacre, Marwan Akel, Chadia Haddad, Rony M. Zeenny, Aline Hajj, Pascale Salameh
BMC Medical Education.2023;[Epub] CrossRef - Investigating autistic traits, social phobia, fear of COVID-19, and internet use disorder variables in the context of videoconference fatigue
Yingying Zhang, Shuxia Yao, Cornelia Sindermann, Dmitri Rozgonjuk, Menghan Zhou, René Riedl, Christian Montag
Telematics and Informatics Reports.2023; 11: 100067. CrossRef - Factors influencing farmers' forestland-use changes over 15 years (2005–2020) in Thua Thien Hue province, Vietnam
T.P.T. Pham, N.T. Tran, C.A. Kull, R.T. Shackleton, R. Cochard, T.H.M. Nguyen, T.D. Ngo, T.H.V. Nguyen, Q.C. Tran, T.T.T. Vu
International Forestry Review.2023; 25(1): 71. CrossRef - Validity of the Greek NMP-Q and Sociodemographic Determinants of Nomophobia Among University Students
Charalambos Gnardellis, Venetia Notara, Elissavet Vagka, Vasilis Gialamas, Areti Lagiou
International Journal of Human–Computer Interaction.2023; 39(4): 842. CrossRef - Associations between attentional biases to fearful faces and social-emotional development in infants with and without an older sibling with autism
Jennifer B. Wagner, Brandon Keehn, Helen Tager-Flusberg, Charles A. Nelson
Infant Behavior and Development.2023; 71: 101811. CrossRef - The role of demographic factors on religious beliefs: Evidence from five countries
Walton Wider, Jem Cloyd M. Tanucan, Xiaole Wu, Christine Mutua, Nicholas Tze Ping Pang, Gabriel Hoh Teck Ling, Charoline Cheisviyanny
F1000Research.2023; 12: 372. CrossRef - Association between Migraine and Workplace Social Support in the Social Context of China: Using a Validated Chinese Version of the DCSQ
Du Wei, Yue Chang, Xiaolong Lu, Xingying Fan, Jiaqi Hu, Otilia Manta, Mohammed K. A. Kaabar
Healthcare.2023; 11(2): 171. CrossRef - The mediating roles of coping styles and academic burnout in the relationship between stressors and depressive symptoms among Chinese postgraduates
Hong Shi, Hanfang Zhao, Minfu He, Zheng Ren, Shixun Wang, Li Cui, Jieyu Zhao, Wenjun Li, Yachen Wei, Wenjing Zhang, Ziqiang Chen, Hongjian Liu, Xiumin Zhang
PeerJ.2023; 11: e16064. CrossRef - Clinical usability of the Story-Based Empathy Task (SET) in non-demented ALS patients
Edoardo Nicolò Aiello, Federica Solca, Silvia Torre, Eleonora Colombo, Alessio Maranzano, Marco Olivero, Francesco Scheveger, Claudia Morelli, Alberto Doretti, Federico Verde, Roberta Ferrucci, Sergio Barbieri, Francesca Mameli, Alberto Priori, Vincenzo S
Neurological Sciences.2023; 44(9): 3181. CrossRef - Prediction of Early Recurrence Following CRS/HIPEC in Patients With Disseminated Appendiceal Cancer
Gopika SenthilKumar, Jennifer Merrill, Ugwuji N. Maduekwe, Jordan M. Cloyd, Keith Fournier, Daniel E. Abbott, Nabeel Zafar, Sameer Patel, Fabian Johnston, Sean Dineen, Joel Baumgartner, Travis E. Grotz, Shishir K. Maithel, Mustafa Raoof, Laura Lambert, Ry
Journal of Surgical Research.2023; 292: 275. CrossRef - Social anxiety and interpersonal risk for suicidal ideation: A longitudinal daily diary analysis
Bradley A. Brown, Jonathan Rottenberg, Fallon R. Goodman
Suicide and Life-Threatening Behavior.2023; 53(6): 968. CrossRef - Modern homophobia among heterosexual Romanian adults: the roles of sexual orientation beliefs, religiosity, perceived social roles, and social media use
Georgiana Lăzărescu, Adina Karner-Hutuleac, Alexandra Maftei
Frontiers in Psychology.2023;[Epub] CrossRef - Sense of belonging in engineering and identity centrality among undergraduate students at Hispanic‐Serving Institutions
Anita Patrick, Madison Andrews, Catherine Riegle‐Crumb, Meagan R. Kendall, John Bachman, Vignesh Subbian
Journal of Engineering Education.2023; 112(2): 316. CrossRef - Analysis of radon concentration in ground water and estimation of associated health risks in Purulia Municipality, West Bengal, India
Joydeep Mukherjee, Sayantan Mitra, Sushanta Sutradhar, Saheli Chowdhury, Sonjoy Mondal, Argha Deb, Chiranjib Barman
Arabian Journal of Geosciences.2023;[Epub] CrossRef - Validity and diagnostics of the Italian version of the Montreal Cognitive Assessment (MoCA) in non-demented Parkinson’s disease patients
Alfonsina D’Iorio, Edoardo Nicolò Aiello, Marianna Amboni, Carmine Vitale, Federico Verde, Vincenzo Silani, Nicola Ticozzi, Andrea Ciammola, Barbara Poletti, Gabriella Santangelo
Aging Clinical and Experimental Research.2023; 35(10): 2157. CrossRef - Students’ perception of written, audio, video and face-to-face reflective approaches for holistic competency development
Cecilia KY Chan, Hannah YH Wong
Active Learning in Higher Education.2023; 24(3): 239. CrossRef - Teleneuropsychology: normative data for the assessment of memory in online settings
Ezia Rizzi, Michela Vezzoli, Sara Pegoraro, Alessio Facchin, Veronica Strina, Roberta Daini
Neurological Sciences.2023; 44(2): 529. CrossRef - Institutional anomie theory and gambling-related crime: An empirical test in Macau
Mengliang Dai, Xiaoyu Zhuang, Ting Kin Ng
Journal of Criminology.2023; 56(2-3): 335. CrossRef - Hidden in Plain Sight: Gender Bias and Heteronormativity in Dutch Textbooks
Tessa M. van de Rozenberg, Marleen G. Groeneveld, Daudi P. van Veen, Lotte D. van der Pol, Judi Mesman
Educational Studies.2023; 59(3): 299. CrossRef - The good, the bad, and the utilitarian: attitudes towards genetic testing and implications for disability
Alexandra Maftei, Oana Dănilă
Current Psychology.2023; 42(16): 13589. CrossRef - Association Between Illness Perception and Adherence to Treatment in Slovak Patients With Hypertension
Mária Sováriová Soósová, Renáta Suchanová, Valéria Parová, Antónia Ulbrichtová, Olívia Kopčová, Kvetoslava Rimárová
Journal of Cardiovascular Nursing.2023; 38(5): 433. CrossRef - The conditional effect of family resilience on family quality of life during the Covid-19 pandemic
Tery Setiawan, Ria Wardani, Ellen Theresia
F1000Research.2023; 11: 1279. CrossRef - Women with more severe premenstrual syndrome have an enhanced anticipatory reward processing: a magnetoencephalography study
Lulu Hou, Yao Meng, Jiahong Gao, Ming Li, Renlai Zhou
Archives of Women's Mental Health.2023; 26(6): 803. CrossRef - Genome-wide association study for temperature response and photo-thermal interaction of flowering time in soybean using a panel of cultivars with diverse maturity groups
Tingting Wu, Huiwen Wen, Xinyue Zhang, Hongchang Jia, Cailong Xu, Wenwen Song, Bingjun Jiang, Shan Yuan, Shi Sun, Cunxiang Wu, Tianfu Han
Theoretical and Applied Genetics.2023;[Epub] CrossRef - Measuring Vulnerability in Grief: The Psychometric Properties of the Italian Adult Attitude to Grief Scale
Alessio Gori, Eleonora Topino, Pierluigi Imperatore, Alessandro Musetti, Julius Sim, Linda Machin
European Journal of Investigation in Health, Psychology and Education.2023; 13(6): 975. CrossRef - The effect of abdominal bracing on respiration during a lifting task: a cross-sectional study
Martin Sembera, Andrew Busch, Alena Kobesova, Barbora Hanychova, Jan Sulc, Pavel Kolar
BMC Sports Science, Medicine and Rehabilitation.2023;[Epub] CrossRef - Sustainable plastics waste management framework based on the analysis of people’s awareness, knowledge, attitude, skills, and action: development of sustainable plastics waste management approaches
R. Y. Paquibut, M. C. Legion, A. R. M. Islam, I. S. Chaudhry, L. Gernal
International Journal of Environmental Science and Technology.2023; 20(9): 10217. CrossRef - Psychometric and clinical evaluation of schizophrenia remission criteria in outpatients with psychotic disorders
Karolina Sakinyte, Christopher Holmberg
BMC Psychiatry.2023;[Epub] CrossRef - Resource loss, coping strategies and post-traumatic stress disorder symptoms in survivors of the 2020 Croatia earthquake
Ajana Löw, Martina Lotar Rihtarić, Ivana Vrselja
BMC Psychology.2023;[Epub] CrossRef - Analysis of Non-Destructive Indicating Properties for Predicting Compressive Strengths of Dendrocalamus sericeus Munro Bamboo Culms
Panumat Tangphadungrat, Chayanon Hansapinyo, Chinnapat Buachart, Teewara Suwan, Suchart Limkatanyu
Materials.2023; 16(4): 1352. CrossRef - Examining the influential components of tourists' intention to use travel apps: the importance–performance map analysis
Pipatpong Fakfare, Noppadol Manosuthi
Journal of Hospitality and Tourism Insights.2023; 6(3): 1144. CrossRef - Role limitations in mothers living with depression: Links with children's academic achievement
Kevin M. Wagner, Carmen R. Valdez
Journal of Applied Developmental Psychology.2023; 86: 101536. CrossRef - Physical Fitness Among Adolescents Who are Hispanic With Overweight or Obesity
Roberto M. Benzo, Sara M. St. George, Sarah E. Messiah, Padideh Lovan, Rafael Leite, Anmol Patel, Tae K. Lee, Guillermo J. Prado
Pediatric Physical Therapy.2023; 35(2): 252. CrossRef - Moderating effects of suicide resilience and meaning in life on the association between entrapment and suicidal ideation in Chinese patients with ovarian cancer: a cross-sectional study
Yinying Zhang, Xiaoping Ding, Jie Chen, Yilan Liu, Gang Wang, Deying Hu
BMC Psychiatry.2023;[Epub] CrossRef - Effects of oxytocin pathway gene polymorphisms and adverse childhood experiences on emotion recognition in schizophrenia spectrum disorders
M.V. Alfimova, V.A. Mikhailova, M.V. Gabaeva, V.V. Plakunova, T.V. Lezheiko, V.E. Golimbet
S.S. Korsakov Journal of Neurology and Psychiatry.2023; 123(9): 90. CrossRef - Chinese version of comprehensive early childhood parenting questionnaire (CECPAQ-CV): Factor structure, reliability, and validity
Shuyang Dong, Judith Semon Dubas, Maja Deković, Zhengyan Wang
Current Psychology.2023; 42(19): 16082. CrossRef - REKLAM GÜVENİRLİĞİ VE REKLAMA YÖNELİK TUTUM BAĞLAMINDA SOSYAL MEDYA OKURYAZARLIK BECERİLERİNİN İNCELENMESİ
Betül ÇEPNİ ŞENER, Engin COŞKUN
Intermedia International E-journal.2023; 10(19): 332. CrossRef - Does heart rate variability mediate the association between chronic stress, cardiorespiratory fitness, and working memory in young adults?
Vera Nina Looser, Sebastian Ludyga, Markus Gerber
Scandinavian Journal of Medicine & Science in Sports.2023; 33(5): 609. CrossRef - The involvement of the semantic neural network in rule identification of mathematical processing
Mengyi Li, Yujie Lu, Xinlin Zhou
Cortex.2023; 164: 11. CrossRef - Ideological Mate-guarding: Sexual Jealousy and Mating Strategy Predict Support for Female Honor
Tom R. Kupfer, Pelin Gul
Evolutionary Psychology.2023;[Epub] CrossRef - Social jetlag longitudinally predicts internalizing and externalizing behavior for adolescent females, but not males
Anne Conway, Alison L. Miller
Chronobiology International.2023; 40(10): 1404. CrossRef - The Effect of Trait Anxiety on Bedtime Procrastination: the Mediating Role of Self-Control
Chengwei Zhang, Dexin Meng, Liwei Zhu, Xiaohan Ma, Jing Guo, Yiming Fu, Ying Zhao, Haiyan Xu, Li Mu
International Journal of Behavioral Medicine.2023; 30(2): 260. CrossRef - Celebrity involvement and film tourist loyalty: Destination image and place attachment as mediators
Bin Zhou, Qihao Xiong, Ping Li, Siyi Liu, Ling-en Wang, Chris Ryan
Journal of Hospitality and Tourism Management.2023; 54: 32. CrossRef - Health anxiety, death anxiety and coronaphobia: Predictors of postpartum depression symptomatology during the COVID-19 pandemic
Ana-Maria Andrei, Rebecca Webb, Violeta Enea
Midwifery.2023; 124: 103747. CrossRef - Prevalence and determinants of Italian physicians’ burnout in the “post-COVID-19” era
Elena Fiabane, Simona Margheritti, Edoardo Nicolò Aiello, Stefano Magnone, Massimo Miglioretti, Paola Gabanelli, Ines Giorgi
International Archives of Occupational and Environmental Health.2023; 96(3): 377. CrossRef - Beyond illness perception: the effects of psychological flexibility when coping with a chronic medical condition
Gil Zukerman, Maya Maor, Tamar Reichard, Shulamit Ben-Itzhak
Psychology, Health & Medicine.2023; 28(7): 1795. CrossRef - Cross-cultural translation, adaptation, and validation of the stroke-specific quality of life (SSQOL) scale 2.0 into Amharic language
Dechasa Imiru Wayessa, Mulugeta Bayisa Chala, Solomon Fasika Demissie, Abey Bekele Abebe, Balamurugan Janakiraman, Sisay Deme, Moges Gashaw
Health and Quality of Life Outcomes.2023;[Epub] CrossRef - A Multi-Informant Approach Testing an Expanded Home Numeracy Mode
Paola Bonifacci, Diego Compiani, Viola Ravaldini, Benedetta Peri, Alexandra Affranti, Valentina Tobia
Education Sciences.2023; 13(3): 278. CrossRef - Entrepreneurial role models and college students’ entrepreneurial calling: A moderated mediation model
Dongmei Jin, Xiaomeng Liu, Fuqin Zhang, Zhiyi Wen
Frontiers in Psychology.2023;[Epub] CrossRef - Gender and age differences in the anticipated acceptance of automated vehicles: insights from a questionnaire study and potential for application
Klemens Weigl, Marco Steinhauser, Andreas Riener
Gender, Technology and Development.2023; 27(1): 88. CrossRef - A cross-sectional nationwide survey of guideline based syncope units in the Netherlands: the SU-19 score—a novel validation for best practices
Steven van Zanten, Jelle S Y de Jong, Mike G Scheffer, Evert C A Kaal, Joris R de Groot, Frederik J de Lange
Europace.2023;[Epub] CrossRef - Clima escolar y acción docente para intervenir en eventos de violencia escolar, resultados del Programa Nacional de Convivencia Escolar en el Noroeste de México
Cesar Alan Flores Partida, José Ángel Vera Noriega, Jesús Tánori Quintana
Revista de Estudios y Experiencias en Educación.2023; 22(48): 12. CrossRef - Beliefs about medication after hospital discharge in geriatric patients with polypharmacy
Laura Mortelmans, Eva Goossens, Tinne Dilles
Geriatric Nursing.2022; 43: 280. CrossRef - Young children’s voices in an unlocked Sweden during the COVID-19 pandemic
M. Jenholt Nolbris, S. Ragnarsson, A.-L. Brorsson, M. Garcia de Avila, M. Forsner, I. Kull, A. L. Olinder, J. Mattson, S. Nilsson, A.-C. Rullander, L.-L. Rydström, P. Olaya-Contreras, M. Berghammer
Scandinavian Journal of Public Health.2022; 50(6): 693. CrossRef - Assessing the Mediating Role of Safety Communication Between Safety Culture and Employees Safety Performance
Gehad Mohammed Ahmed Naji, Ahmad Shahrul Nizam Isha, Abdulsamad Alazzani, Muhammad Shoaib Saleem, Mohammed Alzoraiki
Frontiers in Public Health.2022;[Epub] CrossRef - Applying ICD-11 criteria of Gaming Disorder to identify problematic video streaming in adolescents: Conceptualization of a new clinical phenomenon
Kerstin Paschke, Ann-Kathrin Napp, Rainer Thomasius
Journal of Behavioral Addictions.2022;[Epub] CrossRef - A novel approach based on combining deep learning models with statistical methods for COVID-19 time series forecasting
Hossein Abbasimehr, Reza Paki, Aram Bahrini
Neural Computing and Applications.2022; 34(4): 3135. CrossRef - Teacher burnout and demographic variables as predictors of teachers’ enthusiasm
Gamze KASALAK, Miray DAĞYAR
Participatory Educational Research.2022; 9(2): 280. CrossRef - Diferencias de actividad electromiográfica abdominal en el entrenamiento de core
Fares Silhi-Vargas, José Bruneau-Chávez, Victor Rifo-Contreras, Roberto Lagos-Hernández
Salud UIS.2022;[Epub] CrossRef - Attachment styles and their association with aggression, hostility, and anger in Lebanese adolescents: a national study
Elise Maalouf, Pascale Salameh, Chadia Haddad, Hala Sacre, Souheil Hallit, Sahar Obeid
BMC Psychology.2022;[Epub] CrossRef - Comparison of frontal QRS-T angle in patients with schizophrenia and healthy volunteers
Atilla Tekin, Zülkif Tanrıverdi, Yaşar Kapıcı, Bulut Güc, Oğuz Karamustafalıoğlu
Journal of Psychiatric Research.2022; 149: 76. CrossRef - Virtual Reality Greenspaces: Does Level of Immersion Affect Directed Attention Restoration in VR Environments?
Denise Dillon, Jiaying Cai
J.2022; 5(3): 334. CrossRef - Examining broad intellectual abilities obtained within an mTurk internet sample
Zachary C. Merz, John W. Lace, Alexander M. Eisenstein
Current Psychology.2022; 41(4): 2241. CrossRef - Sex differences in blushing and eye contact in mixed versus same-sex dyads
Peter D. Drummond
Journal of Behavioral and Cognitive Therapy.2022; 32(2): 145. CrossRef - Postural-respiratory function of the diaphragm assessed by M-mode ultrasonography
Martin Sembera, Andrew Busch, Alena Kobesova, Barbora Hanychova, Jan Sulc, Pavel Kolar, Yaodong Gu
PLOS ONE.2022; 17(10): e0275389. CrossRef - Yoga at Every Size: A Preliminary Evaluation of a Brief Online Size-Inclusive Yoga and Body Gratitude Journaling Intervention to Enhance Positive Embodiment in Higher Weight College Women
Jennifer B. Webb, Meagan P. Padro, Erin Vinoski Thomas, Alexandria E. Davies, Lena Etzel, Courtney B. Rogers, Natalia I. Heredia
Frontiers in Global Women's Health.2022;[Epub] CrossRef - Regional Differences in the Perception of Daylit Scenes across Europe Using Virtual Reality. Part II: Effects of Façade and Daylight Pattern Geometry
K. Chamilothori, J. Wienold, C. Moscoso, B. Matusiak, M. Andersen
LEUKOS.2022; 18(3): 316. CrossRef - Exploratory and Confirmatory Factor Analysis for Disposition Levels of Computational Thinking Instrument Among Secondary School Students
Saralah Sovey, Kamisah Osman, Mohd Effendi Ewan Mohd-Matore
European Journal of Educational Research.2022; volume-11-(volume-11-): 639. CrossRef - The Mental Health of Health Care Workers in the UK During COVID-19: The Prevalence of Anxiety, Depression, and Stress
Ravi Chotalia, Mohammed J. Abbas, Alisha Aggarwal
Indian Journal of Occupational and Environmental Medicine.2022; 26(4): 273. CrossRef - The relationship between responsibility attribution and session outcomes: Two‐dimension attribution and two‐person perspective
Lizu Lai, Qiwu Sun, Wenzhen Zhu, Zhihong Ren
Clinical Psychology & Psychotherapy.2022; 29(6): 1928. CrossRef - Can Visually Impaired Use Gestures to Interact With Computers? A Cognitive Load Perspective
Gourav Modanwal, Shashi Bhushan Rai, Aishwarya Jaiswal, Tushar Singh, Kishor Sarawadekar
IEEE Transactions on Human-Machine Systems.2022; 52(2): 267. CrossRef - The structure and correlates of the 20-item Maternal-Fetal Attachment Scale in a population-based sample of Hungarian expectant women
Melinda Pohárnok, Krisztina Kopcsó, Petra Ibolya Polgár
Midwifery.2022; 112: 103422. CrossRef - Do different cognitive domains mediate the association between moderate‐to‐vigorous physical activity and adolescents’ off‐task behaviour in the classroom?
Sebastian Ludyga, Markus Gerber, Serge Brand, Wenke Möhring, Uwe Pühse
British Journal of Educational Psychology.2022;[Epub] CrossRef - Measuring and Validating the Factors Influenced the SME Business Growth in Germany—Descriptive Analysis and Construct Validation
Hosam Azat Elsaman, Nourhan El-Bayaa, Suriyakumaran Kousihan
Data.2022; 7(11): 158. CrossRef - The effect of childhood maltreatment on college students’ depression symptoms: The mediating role of subjective well-being and the moderating role of MAOA gene rs6323 polymorphism
Yiqiu Hu, Zihao Zeng, Liyi Peng, Lin Zhan, Shuangjin Liu, Xiaoyou Ouyang, Daoqun Ding, Zhihua Li
European Journal of Developmental Psychology.2022; 19(3): 438. CrossRef - Exploratory Structural Equation Modeling: Practical Guidelines and Tutorial With a Convenient Online Tool for Mplus
Llewellyn E. van Zyl, Peter M. ten Klooster
Frontiers in Psychiatry.2022;[Epub] CrossRef - An analysis of age-standardized suicide rates in Muslim-majority countries in 2000-2019
Bob Lew, David Lester, Kairi Kõlves, Paul S. F. Yip, Ying-Yeh Chen, Won Sun Chen, M. Tasdik Hasan, Harold G. Koenig, Zhi Zhong Wang, Muhamad Nur Fariduddin, Emek Yuce Zeyrek-Rios, Caryn Mei Hsien Chan, Feisul Mustapha, Mimi Fitriana, Housseini Dolo, Burak
BMC Public Health.2022;[Epub] CrossRef - Impact of inlet and outlet opening height variation on the air quality and ventilation efficiency in the on-top wind catcher buildings: A CFD simulation
Ali Akbar Heidari, Hamid Eskandari
Science and Technology for the Built Environment.2022; 28(10): 1420. CrossRef - Criminal Justice Students’ Perceptions of Human Trafficking Victims: Assessing Bias and Helping Behavior
Temilola Salami, Jeeva Babu, Cayla Hari
Journal of Criminal Justice Education.2022; 33(1): 93. CrossRef - Factorial Validity and Internal Consistency of The Sports Imagery Ability Questionnaire (SIAQ) Malaysian Version
Amir Rifaat Abdul Rahman, Hairul Anuar Hashim, Garry Kuan, Adam Abdul Malik
Annals of Applied Sport Science.2022;[Epub] CrossRef - The Influence of Body Investment on Depression in Chinese College Students: A Moderated Mediating Effect
Jingjing Wang, Xiangli Guan, Sumei Yin, Sha Shen, Xuejiao Li, Md Zahir Ahmed, Mary C. Jobe, Oli Ahmed
International Journal of Mental Health Promotion.2022; 24(1): 39. CrossRef - Collective Efficacy as the Conditional Effect of the Relationship between Religiocentrism and Support for Interreligious Violence
Bagus Takwin, Tery Setiawan
Religions.2022; 14(1): 56. CrossRef - Age and depressive symptoms change predict the 4‐year self‐concept trajectory for youth after anxiety treatment
Krister W. Fjermestad, Katarina Bellika, Caroline Matre, Wendy K. Silverman, Gro Janne Wergeland
Journal of Clinical Psychology.2022; 78(11): 2109. CrossRef - The clinical importance of polyp size measurement through two‐dimensional saline infusion sonohysterography prior to hysteroscopic resection in predicting premalignant and malignant endometrial lesions
Serkan Akış, Gürkan Kıran, Ahmet Göçmen
International Journal of Gynecology & Obstetrics.2022; 157(3): 582. CrossRef - Save our surgeons (SOS) – an explorative comparison of surgeons’ muscular and cardiovascular demands, posture, perceived workload and discomfort during robotic vs. laparoscopic surgery
Bernhard Krämer, Felix Neis, Christl Reisenauer, Christina Walter, Sara Brucker, Diethelm Wallwiener, Robert Seibt, Julia Gabriel, Monika A. Rieger, Benjamin Steinhilber
Archives of Gynecology and Obstetrics.2022; 307(3): 849. CrossRef -
Paradoxically protective effect of glucocorticoids on bone mass and fragility fracture in a large cohort: a cross-sectional study
Marwan Bukhari, Nicola Goodson, Maarten Boers
Rheumatology Advances in Practice.2022;[Epub] CrossRef - Unmet needs, anxiety, depression, and quality of life among caregivers of adolescents and young adults with cancer: A cross-sectional study
Qinqin Cheng, Marques S.N. Ng, Kai Chow Choi, Winnie K.W. So
Asia-Pacific Journal of Oncology Nursing.2022; 9(10): 100108. CrossRef - Historical trend and drivers of China’s CO2 emissions from 2000 to 2020
Chong Wei
Environment, Development and Sustainability.2022; 26(1): 2225. CrossRef - Exploring the Effects of Psychopathy and Emotions on Time Estimation, Intertemporal Decision-Making, and Their Neurophysiological Correlates
Diana Moreira, Andreia Azeredo, Susana Barros, Fernando Barbosa
SSRN Electronic Journal.2022;[Epub] CrossRef - Multi‐omics analysis of xylem sap uncovers dynamic modulation of poplar defenses by ammonium and nitrate
Karl Kasper, Ilka N. Abreu, Kirstin Feussner, Krzysztof Zienkiewicz, Cornelia Herrfurth, Till Ischebeck, Dennis Janz, Andrzej Majcherczyk, Kerstin Schmitt, Oliver Valerius, Gerhard H. Braus, Ivo Feussner, Andrea Polle
The Plant Journal.2022; 111(1): 282. CrossRef - ALT KÜLTÜRLER İLE HEDONİK TÜKETİM ARASINDA İLİŞKİNİN İNCELENMESİ: TÜRK TOPLUMU ÜZERİNE BİR UYGULAMA
Yusuf Öcel, Hakan Tahiri Mutlu, Enis Hiçyılmaz
Elektronik Sosyal Bilimler Dergisi.2022; 21(84): 2041. CrossRef - The impact of reminders on implementation intention: A randomized controlled trial
Léonie Messmer, Fabien Fenouillet, Eve Legrand
Applied Cognitive Psychology.2022; 36(6): 1251. CrossRef - Synchrony in Old Age: Playing the Mirror Game Improves Cognitive Performance
Shoshi Keisari, Rinat Feniger-Schaal, Yuval Palgi, Yulia Golland, Anat Gesser-Edelsburg, Boaz Ben-David
Clinical Gerontologist.2022; 45(2): 312. CrossRef - Psychometric Validation of the FACE-Q Craniofacial Module for Facial Nerve Paralysis
Anne F. Klassen, Charlene Rae, Lucas Gallo, Jonathan H. Norris, Kathleen Bogart, David Johnson, Nancy Van Laeken, Heather L. Baltzer, Dylan J. Murray, Marinka L.F. Hol, Teresa O, Karen W.Y. Wong Riff, Stefan J. Cano, Andrea L. Pusic
Facial Plastic Surgery & Aesthetic Medicine.2022; 24(1): 1. CrossRef - Development of a Questionnaire on Intentions to Engage in Dating Violence Among Puerto Rican Residents
Diana M. Padilla Medina, Ohad Gilbar, Jessica R. Williams
Journal of Family Violence.2022; 37(7): 1181. CrossRef - Retrieving Pigment Concentrations Based on Hyperspectral Measurements of the Phytoplankton Absorption Coefficient in Global Oceans
Jing Teng, Tinglu Zhang, Kunpeng Sun, Hong Gao
Remote Sensing.2022; 14(15): 3516. CrossRef - Relationships of familial sexual stigma and family support with internalized homonegativity among lesbian, gay and bisexual individuals: The mediating effect of self-identity disturbance and moderating effect of gender
Chung-Ying Lin, Mark D. Griffiths, Amir H. Pakpour, Ching-Shu Tsai, Cheng-Fang Yen
BMC Public Health.2022;[Epub] CrossRef - Eight years after the 3-3-4 curriculum reform: The current state of undergraduates’ holistic competency development in Hong Kong
Cecilia K.Y. Chan, Lillian Y.Y. Luk
Studies in Educational Evaluation.2022; 74: 101168. CrossRef - Satisfaction as a key antecedent for word of mouth and an essential mediator for service quality and brand trust in international education
Howard Stribbell, Somsit Duangekanong
Humanities and Social Sciences Communications.2022;[Epub] CrossRef - Development and evaluation of India’s first intraspecific Gossypium barbadense cotton recombinant inbred mapping population for extra-long staple fibre traits
S. ANJAN GOWDA, ISHWARAPPA S. KATAGERI, N. V. MOHAN KUMAR, RAJESH S. PATIL
Journal of Genetics.2022;[Epub] CrossRef - Reply - Letter to the editor: Methodological issues on açaí (Euterpe oleracea Mart.) and juçara (Euterpe edulis Mart.) juices improved HDL-c levels and antioxidant defense of healthy adults in a 4-week randomized cross-over study
Patricia Faria Di Pietro, Patrícia de Fragas Hinnig, Cândice Laís Knöner Copetti, Sheyla de Liz, Edson Luiz da Silva
Clinical Nutrition.2022; 41(1): 264. CrossRef - Time Perspective in the Self-regulatory Mechanism of Meaning in Life
Xiaobing Zheng, Wenjing Wang
Journal of Happiness Studies.2022; 23(2): 747. CrossRef - The Work Gratitude Scale: Development and Evaluation of a Multidimensional Measure
Carolyn M. Youssef-Morgan, Llewellyn E. van Zyl, Barbara L. Ahrens
Frontiers in Psychology.2022;[Epub] CrossRef - Association of metabolic comorbidity with myocardial infarction in individuals with a family history of cardiovascular disease: a prospective cohort study
Seokyung An, Sungji Moon, Sue K. Park
BMC Public Health.2022;[Epub] CrossRef - Black swan event small-sample transfer learning (BEST-L) and its case study on electrical power prediction in COVID-19
Chenxi Hu, Jun Zhang, Hongxia Yuan, Tianlu Gao, Huaiguang Jiang, Jing Yan, David Wenzhong Gao, Fei-Yue Wang
Applied Energy.2022; 309: 118458. CrossRef - The Relationship Between Assessment‐Related Stress, Performance, and Gender in a Class Test
Victoria Prokofieva, Svetlana Kostromina, Pascale Brandt‐Pomares, Jean‐François Hérold, Fabien Fenouillet, Jean‐Luc Velay
Mind, Brain, and Education.2022; 16(2): 112. CrossRef - Postural Control When Using an Industrial Lower Limb Exoskeleton: Impact of Reaching for a Working Tool and External Perturbation
Benjamin Steinhilber, Robert Seibt, Monika A. Rieger, Tessy Luger
Human Factors: The Journal of the Human Factors and Ergonomics Society.2022; 64(4): 635. CrossRef - Semiology and determinants of apathy across neurodegenerative motor disorders: A comparison between amyotrophic lateral sclerosis, Parkinson’s and Huntington’s disease
Barbara Poletti, Federica Solca, Sabrina Maffi, Silvia Torre, Laura Carelli, Edoardo Nicolò Aiello, Roberta Ferrucci, Alberto Priori, Alessia Monti, Federico Verde, Nicola Ticozzi, Simone Migliore, Eugenia Scaricamazza, Melissa Casella, Ferdinando Squitie
Frontiers in Aging Neuroscience.2022;[Epub] CrossRef - The Italian telephone-based Verbal Fluency Battery (t-VFB): standardization and preliminary clinical usability evidence
Edoardo Nicolò Aiello, Alice Naomi Preti, Veronica Pucci, Lorenzo Diana, Alessia Corvaglia, Chiara Barattieri di San Pietro, Teresa Difonzo, Stefano Zago, Ildebrando Appollonio, Sara Mondini, Nadia Bolognini
Frontiers in Psychology.2022;[Epub] CrossRef - Induction of A Disintegrin and Metalloproteinase with Thrombospondin motifs 1 by a rare variant or cognitive activities reduces hippocampal amyloid-β and consequent Alzheimer’s disease risk
Yunjie Qiu, Longze Sha, Xiuneng Zhang, Guanjun Li, Wanwan Zhu, Qi Xu
Frontiers in Aging Neuroscience.2022;[Epub] CrossRef - Gendered Racial Microaggressions, Psychosocial Resources, and Depressive Symptoms among Black Women Attending a Historically Black University
Christy L. Erving, Tiffany R. Williams, Whitney Frierson, Megan Derisse
Society and Mental Health.2022; 12(3): 230. CrossRef - Exploring the effect of remixing stories and games on the development of students' computational thinking
Ioannis Vourletsis, Panagiotis Politis
Computers and Education Open.2022; 3: 100069. CrossRef - Bilimsel Hikâyelerle Desteklenen Fen Öğretiminin İlkokul Öğrencilerinin Akademik Başarılarına Etkisi
İbrahim ALPTEKİN, Mutlu Pınar DEMİRCİ GÜLER
Abant İzzet Baysal Üniversitesi Eğitim Fakültesi Dergisi.2022; 22(3): 1041. CrossRef - Compassion Fatigue Among the Intimate Partner Violence and Sexual Assault Workforce: Enhancing Organizational Practice
Rachel J. Voth Schrag, Leila G. Wood, Karin Wachter, Shanti Kulkarni
Violence Against Women.2022; 28(1): 277. CrossRef - The prevalence and related factors of pre‐diabetes and diabetes among overweight and obese children in Urban schools
Kisokanth G, Indrakumar J, Arulpragasam AN, Ilankoon IMPS
National Journal of Community Medicine.2022; 13(1): 27. CrossRef - Emotional resilience and social network site addiction: The mediating role of emotional expressivity and the moderating role of type D personality
Jia Nie, Wendi Li, Jie Long, Pan Zeng, Pengcheng Wang, Li Lei
Current Psychology.2022; 41(4): 2264. CrossRef - Tourist scams, moral emotions and behaviors: impacts on moral emotions, dissatisfaction, revisit intention and negative word of mouth
Jianan Ma, Fangxuan (Sam) Li, Yuanyuan Shang
Tourism Review.2022; 77(5): 1299. CrossRef - Role of resilience in healthcare workers’ distress and somatization during the COVID‐19 pandemic: A cross‐sectional study across Flanders, Belgium
Erik Franck, Eva Goossens, Filip Haegdorens, Nina Geuens, Michael Portzky, Tinneke Tytens, Tinne Dilles, Katrien Beeckman, Olaf Timmermans, Stijn Slootmans, Bart Van Rompaey, Peter Van Bogaert
Nursing Open.2022; 9(2): 1181. CrossRef - Parametric modelling of a wire electrical discharge machining process using path analysis approach
Baneswar Sarker, Shankar Chakraborty
International Journal of Modelling and Simulation.2022; 42(6): 902. CrossRef - Comparison of Stationarity on Ljung Box Test Statistics for Forecasting
Jayeola Dare, Aye O. Patrick, David O. Oyewola
Earthline Journal of Mathematical Sciences.2022; : 325. CrossRef - Exploring Preservice STEM Teachers’ Smartphone Addiction
Alfiya R. Masalimova, Elmira R. Khairullina, Natalya I. Lapidus, Natalia A. Orekhovskaya, Marina R. Zheltukhina, Ekaterina A. Baranova
Contemporary Educational Technology.2022; 14(3): ep371. CrossRef - Nurse students’ competences in interprofessional pharmaceutical care in Europe: Cross-sectional evaluation
Elyne De Baetselier, Nienke E. Dijkstra, Luis M. Batalha, Paulo A. Carvalho Ferreira, Izabela Filov, Vigdis A. Grøndahl, Jana Heczkova, Ann K. Helgesen, Jo Hirdle, Sue Jordan, Petros Kolovos, Gero Langer, Sabina Ličen, Manuel Lillo-Crespo, Alba Malara, Ha
Nurse Education in Practice.2022; 65: 103485. CrossRef - The Reading the Mind in the Eyes Test, Iowa Gambling Task and Interpersonal Reactivity Index: Normative Data in an Italian Population Sample
Ottavia Maddaluno, Edoardo Nicolò Aiello, Camilla Roncoroni, Antonio Prunas, Nadia Bolognini
Archives of Clinical Neuropsychology.2022; 37(5): 929. CrossRef - A database of water chemistry in eastern Siberian rivers
Shiqi Liu, Ping Wang, Qiwei Huang, Olga I. Gabysheva, Zehong Li, Jialing Zhang, Ekaterina S. Kazak, Yu Liu, Tcogto Zh. Bazarzhapov, Raisa N. Shpakova, Viktor A. Gabyshev, Sergey P. Pozdniakov, Natalia L. Frolova
Scientific Data.2022;[Epub] CrossRef - Body Dissatisfaction and Binge Eating: The Moderating Roles of Sweet Taste Reward Sensitivity and Dietary Restraint among Tobacco Product Users
Tyler B. Mason, Anna Dolgon-Krutolow, Kathryn E. Smith, Adam M. Leventhal
International Journal of Environmental Research and Public Health.2022; 19(23): 15523. CrossRef - Examining the Relationship between Sales Force Proactiveness, Network Capability and Sales Performance: Evidence from International Trade Shows
Pedro Mendonça Silva, Victor Ferreira Moutinho, Vera Teixeira Vale
Journal of Promotion Management.2022; 28(5): 559. CrossRef - Redefining luxury service with technology implementation: the impact of technology on guest satisfaction and loyalty in a luxury hotel
Hyejo Hailey Shin, Miyoung Jeong
International Journal of Contemporary Hospitality Management.2022; 34(4): 1491. CrossRef - Teacher judgment (in)accuracy: Differential relations with student progress in writing
Kane Meissel, Esther S. Yao, Frauke Meyer
Contemporary Educational Psychology.2022; 69: 102067. CrossRef - EFL learners’ confidence, attitudes, and practice towards learning pronunciation
Asma Almusharraf
International Journal of Applied Linguistics.2022; 32(1): 126. CrossRef - “The stress can be unbearable, but the good times are like finding gold”: A phase one modelling survey to inform the development of a self-help positive reappraisal coping intervention for caregivers of those with autism spectrum disorder
Deborah Lancastle, Joanna Hill, Susan Faulkner, Alecia L. Cousins, Eric J. Moody
PLOS ONE.2022; 17(3): e0264837. CrossRef - Gender differences in quality of life and exercise motivation of adolescents of average and increased body mass
Miroljub Ivanović, Uglješa Ivanović
Sport - nauka i praksa.2022; 12(2): 49. CrossRef - Using latent profile analysis to uncover the combined role of anxiety sensitivity and test anxiety in students’ state anxiety
Audrey-Ann Journault, Isabelle Plante, Sandrine Charbonneau, Claudia Sauvageau, Charlotte Longpré, Charles-Édouard Giguère, Carolanne Labonté, Kassandra Roger, Rebecca Cernik, Kathryn Everhart Chaffee, Laurence Dumont, Réal Labelle, Sonia J. Lupien
Frontiers in Psychology.2022;[Epub] CrossRef - Preservice Physics Teachers’ Development of Physics Identities: the Role of Multiple Representations
Nuril Munfaridah, Lucy Avraamidou, Martin Goedhart
Research in Science Education.2022; 52(6): 1699. CrossRef - A comprehensive assessment of time overruns in Ghanaian telecom cell site construction
Ernest Marfo Asiedu, Marcia Mkansi, D T Pham
Cogent Engineering.2022;[Epub] CrossRef - Intuitive assessment of spatial navigation beyond episodic memory: Feasibility and proof of concept in middle-aged and elderly individuals
Sophia Rekers, Michael Niedeggen, Amir-Homayoun Javadi
PLOS ONE.2022; 17(9): e0270563. CrossRef - Resource-Strengthening Training for Parents of Adolescents with Problematic Gaming (Res@t-P): A Clinical Pilot Study
Joel Hülquist, Nicole Fangerau, Rainer Thomasius, Kerstin Paschke
International Journal of Environmental Research and Public Health.2022; 19(15): 9495. CrossRef - The modulation of acute stress on model-free and model-based reinforcement learning in gambling disorder
Florent Wyckmans, Nilosmita Banerjee, Mélanie Saeremans, Ross Otto, Charles Kornreich, Laetitia Vanderijst, Damien Gruson, Vincenzo Carbone, Antoine Bechara, Tony Buchanan, Xavier Noël
Journal of Behavioral Addictions.2022; 11(3): 831. CrossRef - Analysis of Particulate Matter (PM10) Behavior in the Caribbean Area Using a Coupled SARIMA-GARCH Model
Esdra Alexis, Thomas Plocoste, Silvere Paul Nuiro
Atmosphere.2022; 13(6): 862. CrossRef - Italian adaptation of the Beaumont Behavioral Inventory (BBI): psychometric properties and clinical usability
Barbara Iazzolino, Debora Pain, Peotta Laura, Edoardo N. Aiello, Marcello Gallucci, Alice Radici, Francesca Palumbo, Antonio Canosa, Cristina Moglia, Andrea Calvo, Gabriele Mora, Adriano Chiò
Amyotrophic Lateral Sclerosis and Frontotemporal Degeneration.2022; 23(1-2): 81. CrossRef - Narsisistik Özellikler ile Empati, Çocukluk Çağı Travmaları ve Utancın İlişkisi
Bengisu Nehir AYDIN
MANAS Sosyal Araştırmalar Dergisi.2022; 11(4): 1615. CrossRef - Developing a Personalised Learning Model Based on Interactive Novels to Improve the Quality of Mathematics Education
Elena V. Soboleva, Khurshidzhon K. Zhumakulov, Kayumzhon P. Umurkulov, Gasanguseyn I. Ibragimov, Lyubov V. Kochneva, Maria O. Timofeeva
Eurasia Journal of Mathematics, Science and Technology Education.2022; 18(2): em2078. CrossRef - Cognition and motor phenotypes in ALS: a retrospective study
Edoardo Nicolò Aiello, Debora Pain, Alice Radici, Kalliopi Marinou Aktipi, Riccardo Sideri, Ildebrando Appollonio, Gabriele Mora
Neurological Sciences.2022; 43(9): 5397. CrossRef - Relationships between anxiety induced by COVID-19 and perceived social support among Iranian pregnant women
Vahideh Behmard, Narjes Bahri, Fatemeh Mohammadzadeh, Ali Delshad Noghabi, Nasrin Bahri
Journal of Psychosomatic Obstetrics & Gynecology.2022; 43(3): 307. CrossRef - Students’ Perceptions in Online Physical Education Learning: Comparison Study of Autonomy, Competence, and Relatedness in Saudi Students during the COVID-19 Lockdown
Mohamed Frikha, Nesrine Chaâri, Nourhen Mezghanni, Majed M. Alhumaid, Mohammed S. Alibrahim
International Journal of Environmental Research and Public Health.2022; 19(22): 15288. CrossRef - The Testamentary Capacity Assessment Tool (TCAT): validation and normative data
Nadia Bolognini, Chiara Gramegna, Antonella Esposito, Edoardo Nicolò Aiello, Teresa Difonzo, Stefano Zago
Neurological Sciences.2022; 43(4): 2831. CrossRef - Validity and reliability of the Turkish version of the Glasgow Sleep Effort Scale
Omer Faruk Uygur, Hilal Uygur, Seockhoon Chung, Oli Ahmed, Dudu Demiroz, Esat Fahri Aydin, Onur Hursitoglu
Sleep Medicine.2022; 98: 144. CrossRef - Travel medicine meets conservation medicine in St. Kitts: Disinhibition, cognitive‐affective inconsistency, and disease risk among vacationers around green monkeys (Chlorocebus sabaeus)
Michael P. Muehlenbein, Kerry M. Dore, Jeffrey Gassen, Vy Nguyen, O. Grace Jolley, Christa Gallagher
American Journal of Primatology.2022;[Epub] CrossRef - Disclosure Recipients’ Perceptions Related to Helping Victims of Dating and Sexual Violence
Victoria A. Mauer, Katie M. Edwards, Emily A. Waterman, Christina M. Dardis, Emily R. Dworkin, Lindsey M. Rodriguez, Sarah E. Ullman
Journal of Interpersonal Violence.2022; 37(23-24): NP21525. CrossRef - Diagnostic properties of the Frontal Assessment Battery (FAB) in Italian healthy adults
Edoardo Nicolò Aiello, Antonella Esposito, Ildebrando Appollonio, Nadia Bolognini
Aging Clinical and Experimental Research.2022; 34(5): 1021. CrossRef - Enrolment in workplace multimodal training programmes: The weight of trainee reactions to previous training experiences
Rachel Chauvin, Nora Yennek, Pauline Laurent, Sonia Lôrant, Fabien Fenouillet
International Journal of Training and Development.2022; 26(2): 315. CrossRef - Feasibility and Usability of Kegel Exercise Pregnancy Training App (KEPT App) among Pregnant Women with Urinary Incontinence
Aida Jaffar, Noor Muhammad, Sherina Mohd Sidik, Novia Admodisastro, Rosliza Abdul Manaf, Chai Foo, Nazhatussima Suhaili
International Journal of Environmental Research and Public Health.2022; 19(6): 3574. CrossRef - Teacher ratings and adolescent students’ perceived social behaviours and gender-role orientations
Shanel Quenneville, Victoria Talwar, Sandra Bosacki
Journal of Gender Studies.2022; 31(4): 444. CrossRef - Eine Kurzversion des Fragebogens zur Beurteilung des eigenen Körpers (FBeK): Ergebnisse aus klinischen und bevölkerungsrepräsentativen Stichproben
Bjarne Schmalbach, Uwe Altmann, Helena Peitsch-Vuorilehto, Elmar Brähler, Bernhard Strauß
PPmP - Psychotherapie · Psychosomatik · Medizinische Psychologie.2022; 72(02): 68. CrossRef - Stigma and Quality of Life in Women With Breast Cancer: Mediation and Moderation Model of Social Support, Sense of Coherence, and Coping Strategies
Hadi Zamanian, Mohammadali Amini-Tehrani, Zahra Jalali, Mona Daryaafzoon, Fatemeh Ramezani, Negin Malek, Maede Adabimohazab, Roghayeh Hozouri, Fereshteh Rafiei Taghanaky
Frontiers in Psychology.2022;[Epub] CrossRef - Psychometric Assessment of the 18-Item Bangla Mental Health Inventory (Bangla MHI-18)
Oli Ahmed, Mark D. Griffiths, Muhammad Alamgir Hossain
Psychological Studies.2022; 67(1): 110. CrossRef - Assaultive trauma, alcohol use, and alcohol‐related consequences among American Indian adolescents
Nichea S. Spillane, Tessa Nalven, Silvi C. Goldstein, Melissa R. Schick, Katelyn T. Kirk‐Provencher, Aayma Jamil, Nicole H. Weiss
Alcoholism: Clinical and Experimental Research.2022; 46(5): 815. CrossRef - Depression and work–family conflict mediating the effects of job stress on chronic pain: a structural equation modelling approach
Maryam Shaygan, Maryam Yazdanpanah
International Journal of Occupational Safety and Ergonomics.2022; 28(4): 2551. CrossRef - Sleeve gastrectomy with transit bipartition in a series of 883 patients with mild obesity: early effectiveness and safety outcomes
Muzaffer Al, Halit Eren Taskin
Surgical Endoscopy.2022; 36(4): 2631. CrossRef - COVID-19 anxiety and quality of life among Iranian nurses
Zohreh Mohamadzadeh Tabrizi, Fatemeh Mohammadzadeh, Arezoo Davarinia Motlagh Quchan, Narjes Bahri
BMC Nursing.2022;[Epub] CrossRef - Trusting COVID-19 vaccines as individual and social goal
Rino Falcone, Alessandro Ansani, Elisa Colì, Marco Marini, Alessandro Sapienza, Cristiano Castelfranchi, Fabio Paglieri
Scientific Reports.2022;[Epub] CrossRef - Cyberstalking Victimization: An Empirical Assessment of RAT Among Female Iranian College Students
Saeed Kabiri, Jaeyong Choi, Seyyedeh Masoomeh (Shamila) Shadmanfaat, Julak Lee
Journal of Interpersonal Violence.2022; 37(9-10): NP8088. CrossRef - Status and related factors of burnout among palliative nurses in China: a cross-sectional study
Yalin Zhang, Jianjun Jiang, Chuanmei Zhu, Chunhua Liu, Chang Guan, Xiaolin Hu
BMC Nursing.2022;[Epub] CrossRef - Measuring Strengths, Opportunities, Aspirations, and Results: Psychometric Properties of the 12-Item SOAR Scale
Matthew L. Cole, Jacqueline M. Stavros, John Cox, Alexandra Stavros
Frontiers in Psychology.2022;[Epub] CrossRef - Analytical Modeling and Empirical Analysis of Binary Options Strategies
Gurdal Ertek, Aysha Al-Kaabi, Aktham Issa Maghyereh
Future Internet.2022; 14(7): 208. CrossRef - The Relationship Between Early Maladaptive Schema and Problematic Mobile Phone Use Among Adolescent Female
Büşra YAĞMUR, Osman ARICAK
Research on Education and Psychology.2022; 6(2): 101. CrossRef - Psychometric evaluation of the Persian version of the Heart Disease Fact Questionnaire (HDFQ) in people with diabetes in Iran
Sedigheh Khanjari, Fereshteh Javaheri Tehrani, Richard Feinn, Julie A. Wagner, Sima Hashemi, Zahra Abedini
Diabetes & Metabolic Syndrome: Clinical Research & Reviews.2022; 16(7): 102563. CrossRef - Psychometric properties of the Persian version of abridged Connor-Davidson Resilience Scale 10 (CD-RISC-10) among older adults
Hassan Rezaeipandari, Asghar Mohammadpoorasl, Mohammad Ali Morowatisharifabad, Abdolreza Shaghaghi
BMC Psychiatry.2022;[Epub] CrossRef - Second Wave of the Study of Taiwanese Caregivers of Children with ADHD in the COVID-19 Pandemic: Intentions to Vaccinate Their Children for COVID-19, and Related Factors
Ching-Shu Tsai, Liang-Jen Wang, Ray C. Hsiao, Cheng-Fang Yen
Vaccines.2022; 10(5): 753. CrossRef - The influence of resilience on social creativity: Chain mediation effects of sense of humor and positive mood
Yadan Li, Chunyu Liu, Yilong Yang, Ying Du, Cong Xie, Shuoqi Xiang, Haijun Duan, Weiping Hu
Psychology in the Schools.2022; 59(8): 1609. CrossRef - The Role of Impulsivity and Reward Deficiency in “Liking” and “Wanting” of Potentially Problematic Behaviors and Substance Uses
Domonkos File, Beáta Bőthe, Bálint File, Zsolt Demetrovics
Frontiers in Psychiatry.2022;[Epub] CrossRef - The Influence of Sociodemographic Characteristics and the Experience of Recreational Divers on the Preference for Diving Sites
Ke Zhang, Anson T. H. Ma, Theresa W. L. Lam, Wei Fang, Lewis T. O. Cheung
Sustainability.2022; 15(1): 447. CrossRef - Validation and Psychometric Properties of the Minnesota Living With Heart Failure Questionnaire in Individuals With Coronary Artery Disease in Lithuania
Julija Gecaite-Stonciene, Julius Burkauskas, Adomas Bunevicius, Vesta Steibliene, Jurate Macijauskiene, Julija Brozaitiene, Narseta Mickuviene, Nijole Kazukauskiene
Frontiers in Psychology.2022;[Epub] CrossRef - Psychometric assessment of the Bangla version of the Bergen Social Media Addiction Scale
Lutfun Naher, Fatema Akhter Hiramoni, Najifa Alam, Oli Ahmed
Heliyon.2022; 8(7): e09929. CrossRef - Local Residents’ Attitudes Toward Reopening Inbound Tourism Amid COVID-19: A Study in Vietnam
Bình Nghiêm-Phú, Hồng Long Phạm
Sage Open.2022;[Epub] CrossRef - How does group-buying website quality for social commerce affect repurchase intention? Evidence from Chinese online users
Zhuo Sun, Hong Zhao, Zongshui Wang
Asia Pacific Journal of Marketing and Logistics.2022; 34(10): 2109. CrossRef - Psychological distress in parents of children with autism spectrum disorder: A cross-sectional study based on 683 mother-father dyads
Fēi Li, Yun Tang, Fei Li, Shuanfeng Fang, Xin Liu, Minyi Tao, Danping Wu, Liping Jiang
Journal of Pediatric Nursing.2022; 65: e49. CrossRef - Clinical features and cognitive sequelae in COVID-19: a retrospective study on N=152 patients
Marina Rita Manera, Elena Fiabane, Debora Pain, Edoardo Nicolò Aiello, Alice Radici, Marcella Ottonello, Mariacristina Padovani, Barbara Ann Wilson, Jessica Fish, Caterina Pistarini
Neurological Sciences.2022; 43(1): 45. CrossRef - Examining Individual Differences in Social Reward Valuation: a Person-Based Approach
Danique Smeijers, Kasia Uzieblo, Jeffrey C. Glennon, Josi M. A. Driessen, Inti A. Brazil
Journal of Psychopathology and Behavioral Assessment.2022; 44(2): 312. CrossRef - Times Are Harsh, Be Kind to Yourself! Anxiety, Life Satisfaction, and the Mediating Role of Self-Compassion
Alexandra Maftei, Georgiana Lãzãrescu
Frontiers in Psychology.2022;[Epub] CrossRef - Disentangling motivation and engagement: Exploring the role of effort in promoting greater conceptual and methodological clarity
Robin P. Nagy, Andrew J. Martin, Rebecca J. Collie
Frontiers in Psychology.2022;[Epub] CrossRef - Sarcasm use in Turkish: The roles of personality, age, gender, and self-esteem
Natalia Banasik-Jemielniak, Piotr Kałowski, Büşra Akkaya, Aleksandra Siemieniuk, Yasemin Abayhan, Duygu Kandemirci-Bayız, Ewa Dryll, Katarzyna Branowska, Anna Olechowska, Melanie Glenwright, Maria Zajączkowska, Magdalena Rowicka, Penny M. Pexman, Peter Ka
PLOS ONE.2022; 17(11): e0276073. CrossRef - How to “Read” a Destination from Images? Machine Learning and Network Methods for DMOs’ Image Projection and Photo Evaluation
Zeya He, Ning Deng, Xiang (Robert) Li, Huimin Gu
Journal of Travel Research.2022; 61(3): 597. CrossRef - Physical activity questionnaire for older children (PAQ-C): Arabic translation, cross-cultural adaptation, and psychometric validation in school-aged children in Saudi Arabia
Mohamed Sherif Sirajudeen, Mohamed Waly, Md. Dilshad Manzar, Mazen Alqahtani, Msaad Alzhrani, Ahmad Alanazi, Radhakrishnan Unnikrishnan, Hariraja Muthusamy, Rashmi Saibannavar, Wafa Alrubaia
PeerJ.2022; 10: e13237. CrossRef - Car Ownership and the Built Environment: A Spatial Modeling Approach
Jerome Laviolette, Catherine Morency, Owen D. Waygood, Konstadinos G. Goulias
Transportation Research Record: Journal of the Transportation Research Board.2022; 2676(3): 125. CrossRef - Developing and validating a university needs instrument to measure the psychosocial needs of university students
Richard Tindle, Paola Castillo, Natalie Doring, Leigh Grant, Royce Willis
British Journal of Educational Psychology.2022; 92(4): 1550. CrossRef - The contribution of bio-psycho-social dimensions on sexual satisfaction in people with spinal cord injury and their partners: an explorative study
Elia Zanin, Sara Salizzato, Edoardo Nicolò Aiello, Carl Froilan D. Leochico, Reynaldo R. Rey-Matias, Paolo Pauletto, Stefano Masiero, Humberto A. Cerrel Bazo
Spinal Cord Series and Cases.2022;[Epub] CrossRef - Readiness for advance care planning and its relationship to coping style in patients with chronic diseases in communities: A cross‐sectional study
Xinru Wang, Yu Sheng
Nursing Open.2022; 9(2): 1332. CrossRef - Psychometric Validation of the Internet Disorder Scale–Short Form in an Italian Adult Sample
Paolo Soraci, Ambra Ferrari, Enrico Bonanno, De Pace Rosanna, Emanuela Repice, Mark D. Griffiths
International Journal of Mental Health and Addiction.2022; 20(5): 2571. CrossRef - Meta-Analysis of Randomized Clinical Trials Evaluating Effectiveness of a Multivitamin Supplementation against Oxidative Stress in Healthy Subjects
Seoyoung Lee, Iksoo Huh, Seunghee Kang, Yea-eun Nam, Youngseo Cho, Md Kamruzzaman, Jina Hong, Oran Kwon, Taesung Park
Nutrients.2022; 14(6): 1170. CrossRef - Okul Öncesi Çalışanlarının Olumsuz Çocukluk Yaşantılarına Dair Farkındalık Düzeyleri ve Müdahale Stratejileri
Aydın OLCAY, Özkan ÖZGÜN
Ege Eğitim Dergisi.2022; 23: 40. CrossRef - Community Mobility and COVID-19 Dynamics in Jakarta, Indonesia
Ratih Oktri Nanda, Aldilas Achmad Nursetyo, Aditya Lia Ramadona, Muhammad Ali Imron, Anis Fuad, Althaf Setyawan, Riris Andono Ahmad
International Journal of Environmental Research and Public Health.2022; 19(11): 6671. CrossRef - Home mirror therapy: a randomized controlled pilot study comparing unimanual and bimanual mirror therapy for improved arm and hand function post-stroke
Daniel Geller, Dawn M. Nilsen, Lori Quinn, Stephen Van Lew, Claribell Bayona, Glen Gillen
Disability and Rehabilitation.2022; 44(22): 6766. CrossRef - Why do Social Workers Leave? A Moderated Mediation of Professionalism, Job Satisfaction, and Managerialism
Ziyu Liu, Hung Wong, Jifang Liu
International Journal of Environmental Research and Public Health.2022; 20(1): 230. CrossRef - Psychometric properties and validation of the English version Giessen Subjective Complaints List (GBB-8)
Katja Petrowski, Markus Zenger, Bjarne Schmalbach, Christina Diane Bastianon, Bernhard Strauss
BMC Psychology.2022;[Epub] CrossRef - Comparison of Normality Tests in Terms of Sample Sizes under Different Skewness and Kurtosis Coefficients
Süleyman DEMİR
International Journal of Assessment Tools in Education.2022; 9(2): 397. CrossRef - Multicomponent Intervention Associated with Improved Emotional and Cognitive Outcomes of Marginalized Unemployed Youth of Latin America
Cristina Crespo-Andrade, Ana Francisca Trueba, María Sol Garcés, Graham Pluck
Social Sciences.2022; 11(4): 155. CrossRef - Replication analysis of the COVID-19 Worry Scale
Rajib Ahmed Faisal, Mary C. Jobe, Oli Ahmed, Tanima Sharker
Death Studies.2022; 46(3): 574. CrossRef - The Effectiveness of Inquiry Based Activities Based on Authentic Learning Approach on 5th Grade Students' Academic Achievement and Creative Problem Solving Skills
İlknur GÜVEN, Cansu NAS
Academy Journal of Educational Sciences.2022; 6(1): 52. CrossRef - Beliefs about food quality attributes, food-related goals and satisfaction with food-related life among the elderly in China: A means-end approach
Rongduo Liu, Marija Banovic, Klaus G. Grunert
Food Quality and Preference.2022; 95: 104367. CrossRef - Predicting hand washing, mask wearing and social distancing behaviors among older adults during the covid-19 pandemic: an integrated social cognition model
Yanping Duan, Borui Shang, Wei Liang, Zhihua Lin, Chun Hu, Julien Steven Baker, Yanping Wang, Jiali He
BMC Geriatrics.2022;[Epub] CrossRef - YETERSİZLİĞE EBEVEYN TEPKİLERİ ÖLÇEĞİ: GELİŞTİRME VE PSİKOMETRİK ÖZELLİKLERİ
Avşar ARDIÇ, Mustafa BALOĞLU, Seray OLÇAY, Şahin KESİCİ
Mehmet Akif Ersoy Üniversitesi Eğitim Fakültesi Dergisi.2022; (63): 333. CrossRef - Dementia is (not) a natural part of ageing: a cross-sectional study on dementia knowledge and misconceptions in Swiss and Italian young adults, adults, and older adults
Deborah Pacifico, Maddalena Fiordelli, Marta Fadda, Sabatini Serena, Giovanni Piumatti, Fabio Carlevaro, Francesca Magno, Giovanni Franscella, Emiliano Albanese
BMC Public Health.2022;[Epub] CrossRef - Autistic traits heighten sensitivity to rejection‐induced social pain
Xinxin Lin, Shiwei Zhuo, Zhouan Liu, Junsong Fan, Weiwei Peng
Annals of the New York Academy of Sciences.2022; 1517(1): 286. CrossRef - Psychological factors in adherence to COVID-19 public health restrictions in Italy: A path model testing depressed mood, anxiety, and co-rumination via cellphone
Michela Balsamo, Karla Klein Murdock, Leonardo Carlucci, Tauseef Ahmad
PLOS ONE.2022; 17(12): e0278628. CrossRef - Validity and diagnostics of the Reading the Mind in the Eyes Test (RMET) in non-demented amyotrophic lateral sclerosis (ALS) patients
Edoardo Nicolò Aiello, Laura Carelli, Federica Solca, Silvia Torre, Roberta Ferrucci, Alberto Priori, Federico Verde, Vincenzo Silani, Nicola Ticozzi, Barbara Poletti
Frontiers in Psychology.2022;[Epub] CrossRef - Assessment of dry eye disease in N95 versus surgical face mask wearers during COVID-19
Shirin Hamed Azzam, Amir Nama, Hanan Badarni, Helena Asael, Wadie Abu Dahoud, Michael Mimouni, Hiba Zayyad
Indian Journal of Ophthalmology.2022; 70(3): 995. CrossRef - Tracking of menstrual cycles and prediction of the fertile window via measurements of basal body temperature and heart rate as well as machine-learning algorithms
Jia-Le Yu, Yun-Fei Su, Chen Zhang, Li Jin, Xian-Hua Lin, Lu-Ting Chen, He-Feng Huang, Yan-Ting Wu
Reproductive Biology and Endocrinology.2022;[Epub] CrossRef - Problematic internet usage: the impact of objectively Recorded and categorized usage time, emotional intelligence components and subjective happiness about usage
Sameha Alshakhsi, Khansa Chemnad, Mohamed Basel Almourad, Majid Altuwairiqi, John McAlaney, Raian Ali
Heliyon.2022; 8(10): e11055. CrossRef - 63 K and 50 K SNP array based high-density genetic mapping and QTL analysis for productivity and fiber quality traits in cotton
S. Anjan Gowda, Ishwarappa S. Katageri, Rajesh S. Patil, P. Sharat Kumar, Gopal J. Tiwari, Satya N. Jena, Samir V. Sawant
Euphytica.2022;[Epub] CrossRef - Psychological distress, depression symptoms and fatigue among Quebec nursing staff during the COVID‐19 pandemic: A cross‐sectional study
José Côté, Marilyn Aita, Maud‐Christine Chouinard, Julie Houle, Mélanie Lavoie‐Tremblay, Lily Lessard, Geneviève Rouleau, Céline Gélinas
Nursing Open.2022; 9(3): 1744. CrossRef - Establishing the Prevalence of Osteomalacia in Arab Adolescents Using Biochemical Markers of Bone Health
Nasser M. Al-Daghri, Sobhy Yakout, Shaun Sabico, Kaiser Wani, Syed Danish Hussain, Naji Aljohani, Suma Uday, Wolfgang Högler
Nutrients.2022; 14(24): 5354. CrossRef - Is pro-environmentalism a privilege? Country development factors as moderators of socio-psychological drivers of pro-environmental behavior
Öykü H. Aral, Jordi López-Sintas
Environmental Sociology.2022; 8(2): 211. CrossRef - Exchange Rate Volatility Effect on Economic Growth under Different Exchange Rate Regimes: New Evidence from Emerging Countries Using Panel CS-ARDL Model
Karim Ameziane, Bouchra Benyacoub
Journal of Risk and Financial Management.2022; 15(11): 499. CrossRef - Peer Victimization, Resilience and Mental Well-Being Among Left-Behind Children: Dose Gender Make a Difference?
Zhiyou Wang, Xinwen Zhang
Psychological Reports.2022; 125(5): 2357. CrossRef - Examining the Role of Source Evaluation in Athlete Advocacy: How Can Advocate Athletes Inspire Public Involvement in Racial Issues?
Waku Ogiso, Hiroaki Funahashi, Yoshiyuki Mano
Social Sciences.2022; 11(8): 372. CrossRef - Gamma Band Oscillations Reflect Sensory and Affective Dimensions of Pain
Yuanyuan Lyu, Francesca Zidda, Stefan T. Radev, Hongcai Liu, Xiaoli Guo, Shanbao Tong, Herta Flor, Jamila Andoh
Frontiers in Neurology.2022;[Epub] CrossRef - Lifestyle indices of body composition and obesity risk and prevalence among multi-ethnic adolescents in Malaysia
Mohamed S. Zulfarina, Razinah Sharif, Sabarul Afian Mokhtar, Ahmad Nazrun Shuid, Isa Naina-Mohamed
Frontiers in Pediatrics.2022;[Epub] CrossRef - Methods and reference data for middle ear transfer functions
M. Koch, T. M. Eßinger, H. Maier, J. H. Sim, L. Ren, N. T. Greene, T. Zahnert, M. Neudert, M. Bornitz
Scientific Reports.2022;[Epub] CrossRef - Evaluating the psychometric properties of the German adaptation of the client attachment to therapist scale
Katja Petrowski, Bjarne Schmalbach, Joram Ronel, Ileana Schmalbach, Elisabeth Olliges
BMC Medical Research Methodology.2022;[Epub] CrossRef - Cerebral laterality of writing in right‐ and left‐handers: A functional transcranial Doppler ultrasound study
Marietta Papadatou‐Pastou, Panagiotis Sampanis, Ioannis Koumzis, Sofia Stefanopoulou, Dionysia Sousani, Athina Tsigkou, Nicholas A. Badcock
European Journal of Neuroscience.2022; 56(2): 3921. CrossRef - Drinking to Fit in: The Effects of Drinking Motives and Self-Esteem on Alcohol Use among Female College Students
Melissa R. Schick, Tessa Nalven, Nichea S. Spillane
Substance Use & Misuse.2022; 57(1): 76. CrossRef - The HAND-Q: Psychometrics of a New Patient-reported Outcome Measure for Clinical and Research Applications
Kyra L. Sierakowski, Nicola R. Dean, Kathleen Evans Sanchez, Philip A. Griffin, Justin C.R. Wormald, Jeremy N. Rodrigues, Olivier Mares, Jussi P. Repo, Sina M. Hulkkonen, Neil V. Shah, Steven Koehler, Gregory I. Bain, Stefan J. Cano, Andrea L. Pusic, Don
Plastic and Reconstructive Surgery - Global Open.2022; 10(1): e3998. CrossRef - The contribution of positive affect and loneliness on readiness and self-efficacy to quit smoking among Spanish-speaking Mexican American smokers
Tatiana Londoño, John R. Moore, Zully C. Guerra, Nazanin M. Heydarian, Yessenia Castro
The American Journal of Drug and Alcohol Abuse.2022; 48(1): 110. CrossRef - Attachment relationships and psychological distress in young adults: The mediating role of self-esteem
Somia Imran, Sophie Jackson
Journal of Affective Disorders Reports.2022; 8: 100328. CrossRef - Problematic Smartphone Use and Its Associations with Sexual Minority Stressors, Gender Nonconformity, and Mental Health Problems among Young Adult Lesbian, Gay, and Bisexual Individuals in Taiwan
Mei-Feng Huang, Yu-Ping Chang, Wei-Hsin Lu, Cheng-Fang Yen
International Journal of Environmental Research and Public Health.2022; 19(9): 5780. CrossRef - Work Ethics and Ethical Attitudes among Healthcare Professionals: The Role of Leadership Skills in Determining Ethics Construct and Professional Behaviors
Fouad Sakr, Chadia Haddad, Rony M. Zeenny, Hala Sacre, Marwan Akel, Katia Iskandar, Aline Hajj, Pascale Salameh
Healthcare.2022; 10(8): 1399. CrossRef - Traditional and Modern Convenience Samples: An Investigation of College Student, Mechanical Turk, and Mechanical Turk College Student Samples
Arne Weigold, Ingrid K. Weigold
Social Science Computer Review.2022; 40(5): 1302. CrossRef - The impacts of conditions and person-organization fit on alliances performance: And the moderating role of intermediary
Hui Sun, You-Yu Dai, Chaochen Zhang, Rok Lee, Su-Sung Jeon, Jin-Hua Chu, María del Carmen Valls Martínez
PLOS ONE.2022; 17(12): e0275863. CrossRef - Caregivers’ Difficulty in Managing Smartphone Use of Children with Attention-Deficit/Hyperactivity Disorder during the COVID-19 Pandemic: Relationships with Caregiver and Children Factors
Jia-In Lee, Ray C. Hsiao, Ching-Shu Tsai, Cheng-Fang Yen
International Journal of Environmental Research and Public Health.2022; 19(9): 5194. CrossRef - The Developmental Crisis Questionnaire (DCQ-12): Psychometric Development and Validation
Nikolay Petrov, Oliver C. Robinson, Jeffrey J. Arnett
Journal of Adult Development.2022; 29(4): 265. CrossRef - Interindividuelle Leistungsdifferenzierung von Musiklehrkräften in Lerngruppen als Voraussetzung für Adaptivität im Musikunterricht
Johannes Hasselhorn, Friedrich Platz, Christian Harnischmacher
Zeitschrift für Erziehungswissenschaft.2022; 25(3): 519. CrossRef - The perceived invalidation of emotion scale (PIES) in a Portuguese sample: a psychometric evaluation and an item response theory analysis
Tânia Brandão, Rute Brites, João Hipólito, Odete Nunes
Current Psychology.2022; 41(11): 7657. CrossRef - Does bait type and bait container configuration influence the performance of remote underwater video systems in temperate freshwater lakes for assessing fish community structure?
D. M. Glassman, A. Chhor, J. C. Vermaire, J. R. Bennett, S. J. Cooke
Hydrobiologia.2022; 849(9): 1981. CrossRef - Measuring physical, cognitive, and emotional aspects of exhaustion with the BOSS II-short version – results from a representative population-based study in Germany
Antonia M. Werner, Bjarne Schmalbach, Markus Zenger, Elmar Brähler, Andreas Hinz, Johannes Kruse, Hanna Kampling
BMC Public Health.2022;[Epub] CrossRef - Structural Anomalies Detection from Electrocardiogram (ECG) with Spectrogram and Handcrafted Features
Hongzu Li, Pierre Boulanger
Sensors.2022; 22(7): 2467. CrossRef - Exposure to Online Racial Discrimination and Traumatic Events Online in Black Adolescents and Emerging Adults
Ashley D. Maxie‐Moreman, Brendesha M. Tynes
Journal of Research on Adolescence.2022; 32(1): 254. CrossRef - Relating Phonological Awareness and Rapid Automatized Naming to Phonological and Orthographic Processing of Written Words: Cross‐sequential Evidence from French
Caroline Vander Stappen, Marie Van Reybroeck
Reading Research Quarterly.2022; 57(3): 1065. CrossRef - Poor Sleep in Inflammatory Bowel Disease Is Reflective of Distinct Sleep Disorders
Jessica K. Salwen-Deremer, Michael T. Smith, Hannah G. Haskell, Colleen Schreyer, Corey A. Siegel
Digestive Diseases and Sciences.2022; 67(7): 3096. CrossRef - Examining Pride Cups as a health promotion resource to address homophobia in Australian men’s sport
Justen O’Connor, Ruth Jeanes, Erik Denison, Karen Lambert, Nadia Bevan
Health Promotion International.2022;[Epub] CrossRef - Assessment of the Resilience of Schools to Disasters in Kermanshah, Iran in 2020
hamed rahimi, Hamed Mohammadi, Khadijeh Hajimiri
Journal of Human, Environment, and Health Promotion.2022; 8(2): 89. CrossRef - Psychometric Testing of the Traditional Chinese Version of the Fear of Progression Questionnaire-Short Form in Cancer Survivors
Hui Lin Cheng, Man Chung Li, Doris Yin Ping Leung
Journal of Nursing Measurement.2022; 30(4): 707. CrossRef - Effects of a Passive Back-Support Exoskeleton on Knee Joint Loading during Simulated Static Sorting and Dynamic Lifting Tasks
Mona Bär, Tessy Luger, Robert Seibt, Julia Gabriel, Monika A. Rieger, Benjamin Steinhilber
International Journal of Environmental Research and Public Health.2022; 19(16): 9965. CrossRef - Digital Health Apps in the Context of Dementia: Questionnaire Study to Assess the Likelihood of Use Among Physicians
Markus Schinle, Christina Erler, Mayumi Kaliciak, Christopher Milde, Simon Stock, Marius Gerdes, Wilhelm Stork
JMIR Formative Research.2022; 6(6): e35961. CrossRef - Internal consistency and convergent validity of the International Spinal Cord Injury Quality of Life Basic Data Set at discharge from first rehabilitation
Maren Westphal, Simon Kunz, Anke Scheel-Sailer, Christine Fekete, Peter Lude, Marcel W. M. Post, Valerie Carrard
Spinal Cord.2022; 60(3): 261. CrossRef - Exploring Residents’ Perceptions towards Tourism Development—A Case Study of the Adjara Mountain Area
Giorgi Gogitidze, Nana Nadareishvili, Rezhen Harun, Iulia D. Arion, Iulia C. Muresan
Sustainability.2022; 15(1): 492. CrossRef - SOCIAL SUPPORT AND STUDENTS’ ATTITUDE TOWARD HOME-BASED EDUCATION
Saniya G. Abirin
Docens Series in Education.2022; 3: 53. CrossRef - Assessing mood and cognitive functioning in acute stroke: clinical usability of a Visual Analogue Mood Scale (VAMS)
Fabrizio Pasotti, Sabrina Serranò, Edoardo Nicolò Aiello, Chiara Gramegna, Matteo Querzola, Marcello Gallucci, Giuseppe Micieli, Allesandra Bollani, Elio Clemente Agostoni, Gabriella Bottini
Neurological Sciences.2022; 43(3): 1741. CrossRef - Attitude, Self-Control, and Prosocial Norm to Predict Intention to Use Social Media Responsibly: From Scale to Model Fit towards a Modified Theory of Planned Behavior
Md Shahzalal, Hamedi Mohd Adnan
Sustainability.2022; 14(16): 9822. CrossRef - Comparing the psychometric properties of two primary school Computational Thinking (CT) assessments for grades 3 and 4: The Beginners' CT test (BCTt) and the competent CT test (cCTt)
Laila El-Hamamsy, María Zapata-Cáceres, Pedro Marcelino, Barbara Bruno, Jessica Dehler Zufferey, Estefanía Martín-Barroso, Marcos Román-González
Frontiers in Psychology.2022;[Epub] CrossRef - Validation of The Scale on Pre-Service Teachers’ Digital Competence to Assist Students with Functional Diversity
Alfiya R. Masalimova, Klavdiya G. Erdyneeva, Anatoly S. Kislyakov, Zhanna M. Sizova, Elena Kalashnikova, Elmira R. Khairullina
Contemporary Educational Technology.2022; 14(4): ep382. CrossRef - Narcissistic grandiosity and risky health behaviors in college students
Sulamunn R. M. Coleman, Michael J. Bernstein, Jacob A. Benfield, Joshua M. Smyth
Journal of American College Health.2022; 70(2): 634. CrossRef - Statistical Assessment of Some Water Quality and Rainfall Data in Ciliwung River, Indonesia
S Aisyah, H Hidayat, D Verawati
IOP Conference Series: Earth and Environmental Science.2022; 1062(1): 012035. CrossRef - Analysing Dynamics of Plant Height of Standard Chysanthemum ‘Baekma’ Using Non-linear Regression Models
Jeong Hyun Lee, Gyu Hyeon Park, Min-Soo Kim
Horticultural Science and Technology.2022; 40(5): 513. CrossRef - Subject matter specific curriculum integration: a quantitative study of finnish student teachers’ integrative content knowledge
Mikko Niemelä
Journal of Education for Teaching.2022; 48(2): 228. CrossRef - A Serdülő Reziliencia Kérdőív (READ) magyar nyelvű adaptációja
Kitti Kóródi, Erzsébet Szél, Éva Szabó
Magyar Pszichológiai Szemle.2022; 77(4): 483. CrossRef - Psychometric Validation of the Athens Insomnia Scale Among Nurses: A Robust Approach Using Both Classical Theory and Rating Scale Model Parameters
Md Dilshad Manzar, Abdulrhman Albougami, Hamid Yimam Hassen, Mohamed Yacin Sikkandar, Seithikurippu R Pandi-Perumal, Ahmed S Bahammam
Nature and Science of Sleep.2022; Volume 14: 725. CrossRef - Death anxiety and burnout in intensive care unit specialists facing the COVID-19 outbreak: The mediating role of obsession with COVID-19 and coronaphobia
Violeta Enea, Octav Sorin Candel, Simona Alexandra Zancu, Andreea Scrumeda, Mariana Bărbuşelu, Alexandra Maria Largu, Carmen Manciuc
Death Studies.2022; 46(10): 2306. CrossRef - Assessing the digital maturity of micro and small enterprises: a focus on an emerging market
Lais Santiago da Costa, Igor Polezi Munhoz, Luciana Pereira, Alessandra Cristina Santos Akkari
Procedia Computer Science.2022; 200: 175. CrossRef - An Experimental Investigation of the Impact of Blame Appraisals and Moral Injury Beliefs on Psychological Outcomes
Joel Hoffman, Angela Nickerson
Cognitive Therapy and Research.2022; 46(2): 319. CrossRef - The impact of communication on consumer knowledge of environmentally sustainable apparel
Jitong Li, Karen K. Leonas
Journal of Fashion Marketing and Management: An International Journal.2022; 26(4): 622. CrossRef - Psychiatric symptoms subsequent to COVID-19 and their association with clinical features: A retrospective investigation
Elena Fiabane, Debora Pain, Edoardo Nicolò Aiello, Alice Radici, Marina Rita Manera, Federica Grossi, Marcella Ottonello, Caterina Pistarini
Psychiatry Research.2022; 316: 114757. CrossRef - A Synergetic Framework for Green and Lean Manufacturing Practices in SMEs: Saudi Arabia Perspective
Wadhah Abualfaraa, Mohammed AlManei, Rashmeet Kaur, Ahmed Al-Ashaab, Patrick McLaughlin, Konstantinos Salonitis
Sustainability.2022; 15(1): 596. CrossRef - Parental practices under the perspective of incarcerated fathers
Sabrina Daiana Cúnico, Damião Soares de Almeida-Segundo, Adolfo Pizzinato
Psico-USF.2022; 27(4): 751. CrossRef - The Frontal Assessment Battery 20 years later: normative data for a shortened version (FAB15)
Ciro Rosario Ilardi, Sergio Chieffi, Chiara Scuotto, Nadia Gamboz, Filomena Galeone, Maria Sannino, Elisabetta Garofalo, Marco La Marra, Bruno Ronga, Alessandro Iavarone
Neurological Sciences.2022; 43(3): 1709. CrossRef - Evaluation of cardiotoxicity and other adverse effects associated with concomitant administration of artemether/lumefantrine and atazanavir/ritonavir-based antiretroviral regimen in patients living with HIV
Sikiru Olatunji Usman, Ibrahim Adekunle Oreagba, AbdulWasiu Busari, Akinwumi Akinyede, Ololade Adewumi, Michael Rotimi Kadri, Olayinka Hassan, Yinka Adeyemi Fashina, Esther Oluwatoyin Agbaje, Sulaimon Alani Akanmu
Saudi Pharmaceutical Journal.2022; 30(5): 605. CrossRef - ALS Cognitive Behavioral Screen-Phone Version (ALS-CBS™-PhV): norms, psychometrics, and diagnostics in an Italian population sample
Edoardo Nicolò Aiello, Antonella Esposito, Ilaria Giannone, Lorenzo Diana, Susan Woolley, Jennifer Murphy, Georgia Christodoulou, Lucio Tremolizzo, Nadia Bolognini, Ildebrando Appollonio
Neurological Sciences.2022; 43(4): 2571. CrossRef - A Drive for Redemption: Relationship Quality as a Mediator Linking Childhood Maltreatment to Symptoms of Social Anxiety and Depression
Michael Fitzgerald
Journal of Adult Development.2022; 29(1): 29. CrossRef - Exploring pain experience and anxiety sensitivity among Latinx adults in a federally qualified health center
Michael J. Zvolensky, Tanya Smit, Andrew H. Rogers, Cameron Matoska, Lorra Garey, Andres G. Viana, Chad Lemaire, Pamella Nizio, Monica Garza, Nubia A. Mayorga, Melissa Ochoa-Perez, Joseph Ditre
Journal of Behavioral Medicine.2022; 45(3): 404. CrossRef - Working memory development in different modalities in children and young adults
Eyal Heled, Roi Israeli, Daniella Margalit
Journal of Experimental Child Psychology.2022; 220: 105422. CrossRef - Green Consumption Values, Social Appreciation, and Purchasing Behavior
Zahide Yeşim Dikici, Metecan Çakrak, Ebru Demirci
Sustainability and Climate Change.2022; 15(3): 189. CrossRef - Influence of personality traits on online self-disclosure: Considering perceived value and degree of authenticity separately as mediator and moderator
Yuxiang Lv, Gege Fang, Xiaoxue Zhang, Yafei Wang, Yihuan Wang
Frontiers in Psychology.2022;[Epub] CrossRef - Does the perception of sustainability matter for environmentally responsible behavior? Empirical evidence from national park residents
Yi Hsien Lin, Tsung Hung Lee
International Journal of Tourism Research.2022; 24(4): 593. CrossRef - The role of religious narratives and religious orientation towards concerns for the natural environment and animal welfare
Dexon Pasaribu, Bagus Takwin, Pim Martens, Randeep Singh
PLOS ONE.2022; 17(8): e0271515. CrossRef - Burnout and psychological symptoms in healthcare workers during the COVID-19 pandemic: Comparisons of different medical professions in a regional hospital in Turkey
Eser Sagaltici, Reyhan Bahçivan Saydam, Mustafa Cetinkaya, Şengül Kocamer Şahin, Suat Hayri Küçük, Ahmet Yaser Müslümanoğlu
Work.2022; 72(3): 1077. CrossRef - Sex estimation in a Turkish population using Purkait’s triangle: a virtual approach by 3-dimensional computed tomography (3D-CT)
Julieta G. García-Donas, Suna Ors, Ercan Inci, Elena F. Kranioti, Oguzhan Ekizoglu, Negahnaz Moghaddam, Silke Grabherr
Forensic Sciences Research.2022; 7(2): 97. CrossRef - Predictors of psychological and physiological measures of graduate student health during COVID-19
Maryam Marashi, Jennifer J. Heisz
Frontiers in Education.2022;[Epub] CrossRef - Osteoporosis knowledge, health beliefs, and self-efficacy in Hong Kong Chinese men
Sue Seen Tsing Lo, Wai Ming Kok
Archives of Osteoporosis.2022;[Epub] CrossRef - ¿Cómo entender la justicia organizacional en tiempos de pandemia? Relación con la disposición al cambio
Mónica García-Rubiano, Ronald Alberto Toro-Tobar, Julián Camilo Sarmiento López, María Constanza Aguilar-Bustamante, Segundo Gonzalo Pasmay Ramos
Acta Colombiana de Psicología.2022; 26(1): 151. CrossRef - Charismatic Tour-Guiding: Scale Development and Validation
Hsiu-Yu Teng, Sheng-Hshiung Tsaur
Journal of Travel Research.2022; 61(7): 1495. CrossRef - Diagnostic properties of the Frontal Assessment Battery (FAB) in Huntington’s disease
Federica Solca, Edoardo Nicolò Aiello, Simone Migliore, Silvia Torre, Laura Carelli, Roberta Ferrucci, Alberto Priori, Federico Verde, Nicola Ticozzi, Sabrina Maffi, Consuelo Ceccarelli, Ferdinando Squitieri, Vincenzo Silani, Andrea Ciammola, Barbara Pole
Frontiers in Psychology.2022;[Epub] CrossRef - Symptom Burden of Children with Cancer and Parental Quality of Life: The Mediating Role of Parental Stress
Winsome Lam, Su-Fang Li, Yan-Zhi Yi, Ka Ho, Katherine Lam, Doris Leung, Kitty Chan, Jacqueline Ho, Stephen Chan, Hai-Xia Wang, Li Zhou, Yan Yin, Frances Wong
International Journal of Environmental Research and Public Health.2022; 19(16): 9840. CrossRef - Relationship of spirituality, health engagement, health belief and attitudes toward acceptance and willingness to pay for a COVID-19 vaccine
Sri Handayani, Yohanes Andy Rias, Maria Dyah Kurniasari, Ratna Agustin, Yafi Sabila Rosyad, Ya Wen Shih, Ching Wen Chang, Hsiu Ting Tsai, Harapan Harapan
PLOS ONE.2022; 17(10): e0274972. CrossRef - The Effect of Perceived Vaccination on Students’ Online Learning Intentions: A Moderated Mediation Model
Thi Xuan Nong, Hoai Than Nguyen, Thi Thanh Truc Nguyen, Zheng Yan
Human Behavior and Emerging Technologies.2022; 2022: 1. CrossRef - Psychological well-being and adjustment among type 2 diabetes patients: the role of psychological flexibility
Maya Maor, Gil Zukerman, Neta Amit, Tamar Richard, Shulamit Ben-Itzhak
Psychology, Health & Medicine.2022; 27(7): 1456. CrossRef - Increased trunk muscle recruitment during the golf swing is linked to developing lower back pain: A prospective longitudinal cohort study
Samantha-lynn Quinn, Benita Olivier, Warrick McKinon, Chloe Dafkin
Journal of Electromyography and Kinesiology.2022; 64: 102663. CrossRef - Quantifying demand flexibility of building energy systems under uncertainty
Ali Amadeh, Zachary E. Lee, K. Max Zhang
Energy.2022; 246: 123291. CrossRef - Influences of Meteorological Factors on Maize and Sorghum Yield in Togo, West Africa
Raïfatou Affoh, Haixia Zheng, Xuebiao Zhang, Wen Yu, Chunhong Qu
Land.2022; 12(1): 123. CrossRef - Investigating tourists’ intention toward green hotels in Malaysia: a direction on tourist sustainable consumption
Ataul Karim Patwary, Roslizawati Che Aziz, Nik Alif Amri Nik Hashim
Environmental Science and Pollution Research.2022; 30(13): 38500. CrossRef - Mediating effect of self-control in the relationship between psychological distress and food addiction among college students
Yingjie Luo, Yijie Zhang, Xiaodan Sun, Jilian Dong, Jieshu Wu, Xiaofang Lin
Appetite.2022; 179: 106278. CrossRef - Internalized Sexual Stigma among Lesbian, Gay, and Bisexual Individuals in Taiwan: Its Related Factors and Association with Mental Health Problems
Jia-In Lee, Yu-Ping Chang, Ching-Shu Tsai, Cheng-Fang Yen
International Journal of Environmental Research and Public Health.2022; 19(4): 2427. CrossRef - Dijital Hikaye Yönteminin Ortaokul 7. Sınıf Öğrencilerinin "Hücre bölünmeleri" Konusundaki Kavram Yanılgılarını Gidermeye Etkisi
Zehra KÖROĞLU, Sakine Serap AVGIN
Kahramanmaraş Sütçü İmam Üniversitesi Sosyal Bilimler Dergisi.2022; 19(3): 1087. CrossRef - The relationships between social media exposure, food craving, cognitive impulsivity and cognitive restraint
Lisa Filippone, Rebecca Shankland, Quentin Hallez
Journal of Eating Disorders.2022;[Epub] CrossRef - Gait stability in ambulant children with cerebral palsy during dual tasks
Sophie Wist, Lena Carcreff, Sjoerd M. Bruijn, Gilles Allali, Christopher J. Newman, Joel Fluss, Stéphane Armand, Yury Ivanenko
PLOS ONE.2022; 17(6): e0270145. CrossRef - Exploring the impact of lexical context on word association responses
Peter Thwaites
International Journal of Corpus Linguistics.2022; 27(3): 321. CrossRef - An exploratory study; the gap between real reference interval and currently used reference interval of RBC AChE activities in South Korea
Yeonji Seong, Jeongmi Moon, Byeongjo Chun, Yongsoo Cho
Journal of Toxicology and Environmental Health, Part A.2022; 85(18): 739. CrossRef - Association between Self-Stigma and Suicide Risk in Individuals with Schizophrenia: Moderating Effects of Self-Esteem and Perceived Support from Friends
Cian-Ruei Jian, Peng-Wei Wang, Huang-Chi Lin, Mei-Feng Huang, Yi-Chun Yeh, Tai-Ling Liu, Cheng-Sheng Chen, Ya-Ping Lin, Shu-Ying Lee, Ching-Hua Chen, Yun-Chi Wang, Yu-Ping Chang, Yi-Lung Chen, Cheng-Fang Yen
International Journal of Environmental Research and Public Health.2022; 19(22): 15071. CrossRef - Manipulating Stress Responses during Spaceflight Training with Virtual Stressors
Tor Finseth, Michael C. Dorneich, Nir Keren, Warren D. Franke, Stephen B. Vardeman
Applied Sciences.2022; 12(5): 2289. CrossRef - Is the Australian nursing workforce ready to embrace prescribing under supervision? A cross‐sectional survey
Amanda Fox, Fiona Crawford‐Williams, Joseph Ria, Cardiff Lynda, Thoms Debra, Yates Patsy, Nissen Lisa, Raymond Javan Chan
Journal of Advanced Nursing.2022; 78(12): 4082. CrossRef - Water Infrastructure Performance in Sub-Saharan Africa: An Investigation of the Drivers and Impact on Economic Growth
Kokou Dangui, Shaofeng Jia
Water.2022; 14(21): 3522. CrossRef - The relationship between the therapeutic alliance in psychotherapy and suicidal experiences: A systematic review
Charlotte Huggett, Patricia Gooding, Gillian Haddock, Jody Quigley, Daniel Pratt
Clinical Psychology & Psychotherapy.2022; 29(4): 1203. CrossRef - Influence of fish attractant on hooking location of Lutjanus carponotatus and Epinephelus quoyanus caught with soft plastic and hard‐bodied lures
Ben K. Diggles, Ingo Ernst, Stephen Wesche, Katie Scutt
Fisheries Management and Ecology.2022; 29(6): 880. CrossRef - Factors influencing tourists’ shared bicycle loyalty in Hangzhou, China
Bin Zhou, Qihao Xiong, Ping Li, Ling-en Wang, Hu Yu, Jianying Jin
Frontiers in Psychology.2022;[Epub] CrossRef - Effects of the Gratitude Letter and Positive Attention Bias Modification on Attentional Deployment and Emotional States
Bryant M. Stone, John D. Lindt, Norka E. Rabinovich, David G. Gilbert
Journal of Happiness Studies.2022; 23(1): 3. CrossRef - Personality traits and income inequalities in self‐rated oral and general health
Mehrsa Zakershahrak, David Brennan
European Journal of Oral Sciences.2022;[Epub] CrossRef - Trajectories of MMSE and MoCA scores across the healthy adult lifespan in the Italian population
Edoardo Nicolò Aiello, Fabrizio Pasotti, Ildebrando Appollonio, Nadia Bolognini
Aging Clinical and Experimental Research.2022; 34(10): 2417. CrossRef - The development and validation of scales to measure the presence of a teachable moment following a cardiovascular disease event
Michelle Brust, Winifred A. Gebhardt, Nadine A.E. van der Voorde, Mattijs E. Numans, Jessica C. Kiefte-de Jong
Preventive Medicine Reports.2022; 28: 101876. CrossRef - Disinformation Sharing Thrives with Fear of Missing Out among Low Cognitive News Users: A Cross-national Examination of Intentional Sharing of Deep Fakes
Saifuddin Ahmed
Journal of Broadcasting & Electronic Media.2022; 66(1): 89. CrossRef - Plasma metabolite profiles related to plant-based diets and the risk of type 2 diabetes
Fenglei Wang, Megu Y. Baden, Marta Guasch-Ferré, Clemens Wittenbecher, Jun Li, Yanping Li, Yi Wan, Shilpa N. Bhupathiraju, Deirdre K. Tobias, Clary B. Clish, Lorelei A. Mucci, A. Heather Eliassen, Karen H. Costenbader, Elizabeth W. Karlson, Alberto Ascher
Diabetologia.2022; 65(7): 1119. CrossRef - How do undergraduates perceive the use of assessment? A study in higher education
Diana Pereira, Irene Cadime, Gavin Brown, Maria Assunção Flores
European Journal of Higher Education.2022; 12(1): 1. CrossRef - The mediating role of maladaptive cognitive schemas regarding the relationship between parenting styles and chronic pain in adolescents: a structural equation modelling approach
Saghar Salari, Maryam Shaygan, Giti Setoodeh
Child and Adolescent Psychiatry and Mental Health.2022;[Epub] CrossRef - Evaluation of traditional rain-fed agricultural terraces for soil erosion control through UAV observation in the middle mountain of Nepal
Chhabi Lal Chidi, Wei Zhao, Pankaj Thapa, Basanta Paudel, Suresh Chaudhary, Narendra Raj Khanal
Applied Geography.2022; 148: 102793. CrossRef - Teaching and Student Evaluation Tasks: Cross-Cultural Adaptation, Psychometric Properties and Measurement Invariance of Work Tasks Motivation Scale for Teachers
Girum Tareke Zewude, Maria Hercz, Ngan Thi Ngoc Duong, Ferenc Pozsonyi
European Journal of Educational Research.2022; volume-11-(volume-11-): 2243. CrossRef - Algılanan Ebeveynlik Biçimlerinin Kişiler Arası Döngüsel Model Üzerinde Temsili
Miray AKYUNUS, Sergen AKBAY
AYNA Klinik Psikoloji Dergisi.2022; 9(1): 160. CrossRef - Do empathy and oxytocin predict responsiveness to a crying infant simulator in expecting and non-expecting couples? A multilevel study
Maria Kaźmierczak, Marinus H. van Ijzendoorn, Marian Bakermans-Kranenburg
Attachment & Human Development.2022; 24(5): 624. CrossRef - Mental Health Help-Seeking Experience and Attitudes in Asian American, Multiracial American, and White American Emerging Adults
Lisa Nakamura, Duckhyun Jo, Akihiko Masuda
International Journal for the Advancement of Counselling.2022; 44(3): 432. CrossRef - Effectiveness of an online positive psychology intervention among Tunisian healthcare students on mental health and study engagement during the Covid‐19 pandemic
Imen Krifa, Quentin Hallez, Llewellyn Ellardus van Zyl, Amel Braham, Jihene Sahli, Selma Ben Nasr, Rebecca Shankland
Applied Psychology: Health and Well-Being.2022; 14(4): 1228. CrossRef - Relationship between Different Dimensions of Workplace Spirituality and Psychological Well-Being: Measuring Mediation Analysis through Conditional Process Modeling
Rizwan Raheem Ahmed, Farwa Abbas Soomro, Zahid Ali Channar, Alharthi Rami Hashem E, Hassan Abbas Soomro, Munwar Hussain Pahi, Nor Zafir Md Salleh
International Journal of Environmental Research and Public Health.2022; 19(18): 11244. CrossRef - Humans modulate arm stiffness to facilitate motor communication during overground physical human-robot interaction
Sambad Regmi, Devin Burns, Yun Seong Song
Scientific Reports.2022;[Epub] CrossRef - Memory of Conflicts and Perceived Threat as Relevant Mediators of Interreligious Conflicts
Tery Setiawan, Jacqueline Mariae Tjandraningtyas, Christina Maria Indah Soca Kuntari, Kristin Rahmani, Cindy Maria, Efnie Indrianie, Indah Puspitasari, Meta Dwijayanthy
Religions.2022; 13(3): 250. CrossRef - Normative data for the Brief Symptom Inventory for patients with Crohn's disease
Shirley Regev, Shmuel Odes, Vered Slonim-Nevo, Ganit Goren, Michael Friger, Dan Greenberg, Hillel Vardi, Doron Schwartz, Ruslan Sergienko, Orly Sarid
Psychology & Health.2022; 37(2): 246. CrossRef - Craving for carbs: food craving and disordered eating in low-carb dieters and its association with intermittent fasting
Maíra Stivaleti Colombarolli, Jônatas de Oliveira, Táki Athanássios Cordás
Eating and Weight Disorders - Studies on Anorexia, Bulimia and Obesity.2022; 27(8): 3109. CrossRef - Psychological processes connecting team identification and social well-being for middle-aged and older adults: moderated mediation of subjective and objective on-field performance
Yuhei Inoue, Daniel Lock, Mikihiro Sato, Daniel C. Funk
Sport Management Review.2022; 25(2): 207. CrossRef - Assessing the prevalence and severity of smartphone addiction in postsecondary students: a brief report
Anna Rudkovska, Wuyou Sui, Jennifer D. Irwin
Journal of American College Health.2022; 70(5): 1292. CrossRef - Brazilian version of Positive Oral Health and Well-Being: cross-cultural adaptation and psychometric analysis
Matheus França Perazzo, Fernanda Ruffo Ortiz, Pablo Alejandro Pérez-Díaz, Georgios Tsakos, Avraham Zini, Arndt Büssing, Yuval Vered, Paulo Antônio Martins Júnior, Ana Flávia Granville-Garcia, Saul Martins Paiva
Brazilian Oral Research.2022;[Epub] CrossRef - Quality of life in young men with androgenetic alopecia: A mixed methods study
Josip Razum, Tena Vukasović Hlupić
Journal of Cosmetic Dermatology.2022; 21(2): 794. CrossRef - Reverse Logistics Strategies and Their Effect on the Competitiveness of Fast-Moving Consumer Goods Firms in South Africa
Mpho Sharon Makgedi Makaleng, Progress Hove-Sibanda
Logistics.2022; 6(3): 56. CrossRef - Ülke, Ürün ve Lider İmajı Ekseninde Türk Vatandaşlarının Rusya ve ABD Algısı: Karşılaştırmalı Bir Saha Çalışması
İbrahim Halil YAŞAR, Yusuf Zafer Can UĞURHAN
İletişim ve Diplomasi.2022; (7): 47. CrossRef - Changes in residents’ attitudes toward tourism and perceptions of tourism contribution pre- and peri-Covid-19 pandemic: role of perceived gratitude and damage
Jing Yin, Eun Joo Kim, Yeong-Hyeon Hwang
Asia Pacific Journal of Tourism Research.2022; 27(6): 637. CrossRef - Borderline Personality Traits and Emotion Regulation Strategies in Adolescents: The Role of Implicit Theories
Jane McLachlan, Mani Mehdikhani, Beth Larham, Luna C. Muñoz Centifanti
Child Psychiatry & Human Development.2022; 53(5): 899. CrossRef - Associations among Perceived Sexual Stigma from Family and Peers, Internalized Homonegativity, Loneliness, Depression, and Anxiety among Gay and Bisexual Men in Taiwan
Huang-Chi Lin, Chih-Cheng Chang, Yu-Ping Chang, Yi-Lung Chen, Cheng-Fang Yen
International Journal of Environmental Research and Public Health.2022; 19(10): 6225. CrossRef - A multi-component, adaptive Working Memory Assessment Battery (WoMAB): validation and norms in an Italian population sample
Fabrizio Pasotti, Giulia De Luca, Edoardo Nicolò Aiello, Chiara Gramegna, Marco Di Gangi, Giuseppe Foderaro, Marcello Gallucci, Elena Biglia, Gabriella Bottini
Neurological Sciences.2022; 43(2): 985. CrossRef - Factors influencing faculty’s online teaching decisions
Gulinna A, Jingrong Xie, Nilufer Korkmaz
Distance Education.2022; 43(3): 426. CrossRef - Measuring health insurance literacy in the Netherlands – First results of the HILM-NL questionnaire
Laurens Holst, Jany J.D.J.M. Rademakers, Anne E.M. Brabers, Judith D. de Jong
Health Policy.2022; 126(11): 1157. CrossRef - Swedish High School Students’ Drug and Alcohol Use Habits throughout 2020
Anis Sfendla, Kourosh Bador, Michela Paganelli, Nóra Kerekes
International Journal of Environmental Research and Public Health.2022; 19(24): 16928. CrossRef - Adaptation of higher education students’ digital skills survey to Russian universities
Nina I. Kryukova, Alexey A. Chistyakov, Tatiana I. Shulga, Leyla B. Omarova, Tatiana V. Tkachenko, Alexey K. Malakhovsky, Nigina S. Babieva
Eurasia Journal of Mathematics, Science and Technology Education.2022; 18(11): em2183. CrossRef - YETİŞKİNLER İÇİN DİJİTAL OYUN BAĞIMLILIĞI ÖLÇEĞİ: TÜRKÇE UYARLAMA, GEÇERLİK VE GÜVENİRLİK ÇALIŞMASI
Levent GÖLLER, Metin PİŞKİN
Trakya Üniversitesi Sosyal Bilimler Dergisi.2022; 24(1): 67. CrossRef - Standing with our hometowns? The relationship between residents' perceived threat from COVID-19 and intention to support tourism recovery in their hometown
Yan Liu, XinYue Cao, Xavier Font, XingPing Cao
Journal of Destination Marketing & Management.2022; 25: 100726. CrossRef - Psychometric Qualities of the Performance Failure Appraisal Inventory–Short Form for Malaysian Undergraduate Students
Chee-Seng Tan, Anna Wen-Huey Ong, Soon-Aun Tan, Su-Wan Gan, Shue-Ling Chong, Sew-Kim Low, Sarvarubini Nainee
Trends in Psychology.2022; 32(3): 839. CrossRef - National identification, social dominance orientation, and attitudes towards Black Pete in the Netherlands: Person- and variable-centered analyses
Daudi van Veen, Rosanneke A. G. Emmen, Judi Mesman
Social Psychological Bulletin.2022;[Epub] CrossRef - Central sensitization in axial spondyloarthritis: An explorative study with quantitative sensory testing and clinical scales
Feyza Nur Yücel, Mehmet Tuncay Duruöz
Modern Rheumatology.2022; 32(6): 1137. CrossRef - Measuring Hispanic Optimism and Personal Expectancy
Richard C. Cervantes, Rosa M. Gonzalez-Guarda, Brian E. McCabe, Gabriela A. Nagy
Hispanic Journal of Behavioral Sciences.2022; 44(4): 267. CrossRef - Psychometric Properties of the Interpersonal Needs Questionnaire-15 in Spanish Adolescents
Sandra Pérez Rodríguez, Joaquín García-Alandete, Blanca Gallego Hernández de Tejada, Verónica Guillén, Jose Heliodoro Marco
Frontiers in Psychiatry.2022;[Epub] CrossRef - Shifting to tele-creative arts therapies during the COVID-19 pandemic: An international study on helpful and challenging factors
Rinat Feniger-Schaal, Hod Orkibi, Shoshi Keisari, Nisha L. Sajnani, Jason D. Butler
The Arts in Psychotherapy.2022; 78: 101898. CrossRef - Free-water diffusion MRI detects structural alterations surrounding white matter hyperintensities in the early stage of cerebral small vessel disease
Carola Mayer, Felix L Nägele, Marvin Petersen, Benedikt M Frey, Uta Hanning, Ofer Pasternak, Elina Petersen, Christian Gerloff, Götz Thomalla, Bastian Cheng
Journal of Cerebral Blood Flow & Metabolism.2022; 42(9): 1707. CrossRef - Reliability and validity assessment of the Mental Health Continuum – Short Form for Bangladeshi adults
Fatema Akhter Hiramoni, Oli Ahmed
Heliyon.2022; 8(1): e08814. CrossRef - The Relationship between Word Difficulty and Frequency: A Response to Hashimoto (2021)
Jeffrey Stewart, Joseph P. Vitta, Christopher Nicklin, Stuart McLean, Geoffrey G. Pinchbeck, Brandon Kramer
Language Assessment Quarterly.2022; 19(1): 90. CrossRef - One‐year cognitive follow‐up of COVID‐19 hospitalized patients
Roberta Ferrucci, Michelangelo Dini, Chiara Rosci, Antonella Capozza, Elisabetta Groppo, Maria R. Reitano, Elisa Allocco, Barbara Poletti, Agostino Brugnera, Francesca Bai, Alessia Monti, Nicola Ticozzi, Vincenzo Silani, Stefano Centanni, Antonella D’Armi
European Journal of Neurology.2022; 29(7): 2006. CrossRef - With or Without You: Beneficial and Detrimental Associations Between Companion Dogs and Human Psychological Adjustment During a COVID-19 Lockdown Phase
Mariely Lima, Teresa Letra Mateus, Karine Silva
Anthrozoös.2022; 35(5): 713. CrossRef - Effects of a multimodal approach to food art therapy on people with mild cognitive impairment and mild dementia
Hyojin Lee, Eunjoo Kim, Ju Young Yoon
Psychogeriatrics.2022; 22(3): 360. CrossRef - Optimized Feature Selection Based on a Least-Redundant and Highest-Relevant Framework for a Solar Irradiance Forecasting Model
Najiya Omar, Hamed Aly, Timothy Little
IEEE Access.2022; 10: 48643. CrossRef - Mathematics Related Belief System and Word Problem-Solving in the Indonesian Context
Achmad Hidayatullah, Csaba Csíkos
Eurasia Journal of Mathematics, Science and Technology Education.2022; 18(4): em2094. CrossRef - Will catering employees’ job dissatisfaction lead to brand sabotage behavior? A study based on conservation of resources and complexity theories
Jiamin Peng, Xiaoyun Yang, Xinhua Guan, Lian Zhou, Tzung-Cheng Huan
International Journal of Contemporary Hospitality Management.2022; 34(5): 1882. CrossRef - Longitudinal Measurement of Empathy in Student Pharmacists
Paul C. Walker, Vincent D. Marshall, Burgunda V. Sweet, Sarah E. Vordenberg
American Journal of Pharmaceutical Education.2022; 86(7): 8752. CrossRef - Mental Health Literacy, Help-Seeking, and Mental Health Outcomes in Women Rugby Players
Shakiba Oftadeh-Moghadam, Paul Gorczynski
Women in Sport and Physical Activity Journal.2022; 30(1): 1. CrossRef - The effect of simultaneous exposure on the attention selection and integration of segments and lexical tones by Urdu-Cantonese bilingual speakers
Jinghong Ning, Gang Peng, Yi Liu, Yingnan Li
Frontiers in Psychology.2022;[Epub] CrossRef - Risk factors in body image dissatisfaction: gender, maladaptive perfectionism, and psychological wellbeing
Richard E. Hicks, Bridget Kenny, Simone Stevenson, Daisy M. Vanstone
Heliyon.2022; 8(6): e09745. CrossRef - The Role of Perceived Servant Leadership in Schools in Predicting Loyalty to Supervisor
Selçuk Demir
European Journal of Educational Management.2022; volume-5-2(volume-5-i): 77. CrossRef - Long-lasting, dissociable improvements in working memory and long-term memory in older adults with repetitive neuromodulation
Shrey Grover, Wen Wen, Vighnesh Viswanathan, Christopher T. Gill, Robert M. G. Reinhart
Nature Neuroscience.2022; 25(9): 1237. CrossRef - Distribution and controlling factors of microplastics in surface sediments of typical deep-sea geomorphological units in the northern South China Sea
Xiaodong Zhang, Zhifei Liu, Yulong Zhao, Pengfei Ma, Christophe Colin, Andrew Tien-Shun Lin
Frontiers in Marine Science.2022;[Epub] CrossRef - Cross-cultural adaptation and validation of the Amharic version of Roland Morris Disability Questionnaire in people with low back pain in Ethiopia
Mulugeta Bayisa Chala, Catherine Donnelly, Yemataw Wondie, Setareh Ghahari, Jordan Miller
Disability and Rehabilitation.2022; 44(19): 5638. CrossRef - Rappresentazioni e atteggiamenti degli insegnanti verso le diagnosi di DSA: costruzione e validazione preliminare di un questionario
Eleonora Florio, Letizia Caso, Ilaria Castelli
RICERCHE DI PSICOLOGIA.2022; (1): 1. CrossRef - Key determinants of quality in the pharmaceutical supply chain
Muhammad Tayyab, Muhammad Usman Awan, Nadeem Irfan Bukhari, Ehsan Sabet
International Journal of Quality & Reliability Management.2022; 39(2): 345. CrossRef - Sense of Coherence and Health-Related Quality of Life in Patients with Multiple Sclerosis: The Role of Physical and Neurological Disability
Joanna Dymecka, Rafał Gerymski, Rafał Tataruch, Mariola Bidzan
Journal of Clinical Medicine.2022; 11(6): 1716. CrossRef - Association between COVID-19 Anxiety and Cognitive Failure and Temperament Components in the Personnel of an Iranian Hospital, Iran, 2021
Rohollah Fallah Madvari, Mohammad Javad Zare Sakhvidi, Fatemeh Kargar Shouroki, Reyhane Sefidkar, Fatemeh Babaee, Mahdi Jafari Nodoushan
Journal of Occupational Health and Epidemiology.2022; 11(3): 187. CrossRef - Short quality of life scale: A cross-cultural validation in Iranian patients with multiple sclerosis
Samira Zarrabi-Ajami, Hadi Zamanian, Mohammadali Amini-Tehrani, Zahra Farhadidanaloo, Razieh Janati Razavi, Azam Abbasi, Saeideh Darbandi, Pegah Chenari
Multiple Sclerosis and Related Disorders.2022; 58: 103411. CrossRef - Oxytocin receptor genotype moderates the association between maternal prenatal stress and infant early self-regulation
Jani Kajanoja, Saara Nolvi, Katri Kantojärvi, Linnea Karlsson, Tiina Paunio, Hasse Karlsson
Psychoneuroendocrinology.2022; 138: 105669. CrossRef - The Prevalence and Psychosocial Correlates of Ketum (Mitragyna speciosa) Use among Individuals on Methadone Maintenance Therapy Programme in Hospital Taiping, Malaysia
Ling Ling Choo, Muhammad Muhsin Ahmad Zahari, Seng Kit Choy, Naemah Abdul Rahim, Rusdi Abd Rashid
Healthcare.2022; 10(4): 746. CrossRef - Beneficial Effect of Methanolic Extract of Frankincense (Boswellia Sacra) on Testis Mediated through Suppression of Oxidative Stress and Apoptosis
Samir Abdulkarim Alharbi, Mohammed Asad, Kamal Eldin Ahmed Abdelsalam, Monjid Ahmed Ibrahim, Sunil Chandy
Molecules.2022; 27(15): 4699. CrossRef - A better but persistently low health status in women with fibromyalgia during the COVID-19 pandemic: a repeated cross-sectional data analysis
Tim Y. Koppert, Henriët van Middendorp, Rinie Geenen
Rheumatology International.2022; 42(6): 967. CrossRef - Relationship between Internet Addiction, Personality Factors, and Emotional Distress among Adolescents in Malaysia
Soh Chou Fu, Nicholas Tze Ping Pang, Walton Wider
Children.2022; 9(12): 1883. CrossRef - Self-Management of Medication on a Cardiology Ward: Feasibility and Safety of the SelfMED Intervention
Toke Vanwesemael, Laura Mortelmans, Koen Boussery, Sue Jordan, Tinne Dilles
International Journal of Environmental Research and Public Health.2022; 19(24): 16715. CrossRef - Diagnostics and clinical usability of the Montreal Cognitive Assessment (MoCA) in amyotrophic lateral sclerosis
Edoardo Nicolò Aiello, Federica Solca, Silvia Torre, Laura Carelli, Roberta Ferrucci, Alberto Priori, Federico Verde, Vincenzo Silani, Nicola Ticozzi, Barbara Poletti
Frontiers in Psychology.2022;[Epub] CrossRef - Sleep–wake patterns and disturbances in Portuguese primary school children: a comparison between 1995 and 2016
Maria Inês Clara, Vanda Clemente, Joana Abrantes, Daniel R. Marques, Maria H. P. Azevedo, Ana Allen Gomes
Sleep and Biological Rhythms.2022; 20(4): 541. CrossRef - Mental Health during COVID-19 Pandemic: The Role of Optimism and Emotional Regulation
Imen Krifa, Llewellyn Ellardus van Zyl, Amel Braham, Selma Ben Nasr, Rebecca Shankland
International Journal of Environmental Research and Public Health.2022; 19(3): 1413. CrossRef - Measuring Attitude toward Chemistry, Biology, and Math at a Hispanic-Serving Institution
Jordan Chang, Erik Jason Menke
Journal of Chemical Education.2022; 99(4): 1758. CrossRef - The impact of penalties on attack frequency in high-level judo matches
Bayram Ceylan, Şükrü Serdar Balcı, Hasan Basri Taşkın, Luis Santos
International Journal of Performance Analysis in Sport.2022; 22(6): 715. CrossRef - Cross-lagged models of health-related quality of life and breastfeeding across different body mass index groups: A three-wave prospective longitudinal study
Ying Lau, Lue Fang, Sarah Su Tin Ho-Lim, Peng Im Lim, Claudia Chi, Sai Ho Wong, Ling Jie Cheng
Midwifery.2022; 112: 103413. CrossRef - The conditional effect of family resilience on family quality of life during the Covid-19 pandemic
Tery Setiawan, Ria Wardani, Ellen Theresia
F1000Research.2022; 11: 1279. CrossRef - Can microfinance-backed entrepreneurship be a holistic empowerment tool for women? Empirical evidence from Kashmir Valley, India
Shagufta Tariq Khan, Mohd Abass Bhat, Mohi-Ud-Din Sangmi
Journal of Business and Socio-economic Development.2022; 2(2): 117. CrossRef - The mediating effect of information sharing on pharmaceutical supply chain integration and operational performance in Ethiopia: an analytical cross-sectional study
Yohannes Birhanu, Tafesse Gizaw, Dawit Teshome, Bekele Boche, Tadesse Gudeta
Journal of Pharmaceutical Policy and Practice.2022;[Epub] CrossRef - Effects of Cultural Intelligence and Imposter Syndrome on School Belonging through Academic Resilience among University Students with Vocational Backgrounds
Shiyong Wu, Wenxin Chen, Wei Chen, Wen Zheng
International Journal of Environmental Research and Public Health.2022; 19(13): 7944. CrossRef - Plasma Protein Levels Analysis in Multiple Sclerosis Sardinian Families Identified C9 and CYP24A1 as Candidate Biomarkers
Andrea Nova, Teresa Fazia, Ashley Beecham, Valeria Saddi, Marialuisa Piras, Jacob L. McCauley, Carlo Berzuini, Luisa Bernardinelli
Life.2022; 12(2): 151. CrossRef - Perceived attitudes of family and peers toward same-sex marriage as a distal sexual minority stressor for gay and bisexual men in Taiwan
Chih-Cheng Chang, Hsin-Yu Lu, Yu-Ping Chang, Ching-Shu Tsai, Cheng-Fang Yen
BMC Public Health.2022;[Epub] CrossRef - A methodology for preprocessing structured big data in the behavioral sciences
Paul A. Brown, Ricardo A. Anderson
Behavior Research Methods.2022; 55(4): 1818. CrossRef - Predictors of intention to receive cervical cancer screening among commercial sex workers in Gondar city, northwest Ethiopia: application of the theory of planned behavior
Habitu Birhan Eshetu, Kegnie Shitu, Simegnew Handebo
BMC Women's Health.2022;[Epub] CrossRef - Why do growth mindsets make you feel better about learning and your selves? The mediating role of adaptability
Nourollah Zarrinabadi, Mohsen Rezazadeh, Mina Karimi, Nigel Mantou Lou
Innovation in Language Learning and Teaching.2022; 16(3): 249. CrossRef - Development and validation of the leadership learning agility scale
Sophie I. M. Bouland-van Dam, Janneke K. Oostrom, Paul G. W. Jansen
Frontiers in Psychology.2022;[Epub] CrossRef - Perceptions of ideal grief and continuing bonds: Undergraduate student survey on persistent complex bereavement disorder
Kaori Wada, Lauren C. Buote, Shizuka Kawamoto
Death Studies.2022; 46(5): 1111. CrossRef - Preschool predictors of learning to read and spell in an additional language: a two-wave longitudinal study in a multilingual context
Cyril Wealer, Silke Fricke, Ariana Loff, Pascale M. J. Engel de Abreu
Reading and Writing.2022; 35(5): 1265. CrossRef - Measuring Guanxi Quality in the Workplace
MiaoHua Chen, Olwen Bedford
Journal of Business and Psychology.2022; 37(3): 581. CrossRef - Relationships between Depression and Executive Functioning in Adolescents: The Moderating Role of Unpredictable Home Environment
Marie L. Gillespie, Uma Rao
Journal of Child and Family Studies.2022; 31(9): 2518. CrossRef - Exploring psychopathy traits on intertemporal decision-making, neurophysiological correlates, and emotions on time estimation in community adults
Diana Moreira, Andreia Azeredo, Susana Barros, Fernando Barbosa
Heliyon.2022; 8(7): e09792. CrossRef - Psychological well-being in US veterans with non-fatal suicide attempts: A multi-cohort population-based study
Bradley A. Brown, Fallon R. Goodman, Robert H. Pietrzak, Jonathan Rottenberg
Journal of Affective Disorders.2022; 314: 34. CrossRef - COVID-19 Stress and Teachers Well-Being: The Mediating Role of Sense of Coherence and Resilience
Girum Tareke Zewude, Sisay Demissew Beyene, Belayneh Taye, Fatiha Sadouki, Maria Hercz
European Journal of Investigation in Health, Psychology and Education.2022; 13(1): 1. CrossRef - Impacts of knowledge expectations on recipients’ continuous cross-project learning intention
Dali Zhao, Yuan Jiang, Chunpei Lin, Xianyue Liu, Yenchun Jim Wu
International Journal of Project Management.2022; 40(2): 120. CrossRef - Translation and Validation of a Brief Health Literacy Instrument for School-Age Children in a Danish Context
Ane H. Bonde, Nanna W. Stjernqvist, Charlotte D. Klinker, Helle T. Maindal, Olli Paakkari, Peter Elsborg
HLRP: Health Literacy Research and Practice.2022;[Epub] CrossRef - The Frontal Assessment Battery (FAB) and its sub-scales: validation and updated normative data in an Italian population sample
Edoardo Nicolò Aiello, Antonella Esposito, Chiara Gramegna, Valentina Gazzaniga, Stefano Zago, Teresa Difonzo, Ildebrando Marco Appollonio, Nadia Bolognini
Neurological Sciences.2022; 43(2): 979. CrossRef - Disembodying language: Actionality does not account for verb processing deficits in Parkinson's disease
Edoardo Nicolò Aiello, Margherita Grosso, Asia Di Liberto, Adele Andriulo, Simona Buscone, Claudia Caracciolo, Monica Ottobrini, Claudio Luzzatti
Journal of Neurolinguistics.2022; 61: 101040. CrossRef - When The New Normal Is Not That New, Why Not Follow? Optimising e-Tourism and e-Marketplaces for Business Events
Ying Ying Tiong, Jamie, Yiee Chiu Suet
International Journal of Business Events and Legacies.2022; : 69. CrossRef - Telephone-based Frontal Assessment Battery (t-FAB): standardization for the Italian population and clinical usability in neurological diseases
Edoardo Nicolò Aiello, Veronica Pucci, Lorenzo Diana, Aida Niang, Alice Naomi Preti, Adriana Delli Ponti, Gaia Sangalli, Stefano Scarano, Luigi Tesio, Stefano Zago, Teresa Difonzo, Ildebrando Appollonio, Sara Mondini, Nadia Bolognini
Aging Clinical and Experimental Research.2022; 34(7): 1635. CrossRef - Thriving or surviving at work: how workplace learning opportunities and subjective career success are connected with job satisfaction and turnover intention?
Eija Elina Lehtonen, Petri Nokelainen, Heta Rintala, Ilmari Puhakka
Journal of Workplace Learning.2022; 34(1): 88. CrossRef - Country Life in the Digital Era: Comparison of Technology Use and Cybercrime Victimization between Residents of Rural and Urban Environments in Slovenia
Igor Bernik, Kaja Prislan, Anže Mihelič
Sustainability.2022; 14(21): 14487. CrossRef - Fostering quality customer service during Covid-19: The role of managers’ oral language, employee work engagement, and employee resilience
Md Karim Rabiul, Pornpisanu Promsivapallop, Rashed Al Karim, Md Ariful Islam, Ataul Karim Patwary
Journal of Hospitality and Tourism Management.2022; 53: 50. CrossRef - Public Stigmatization of People With Intellectual Disability During the COVID-19 Pandemic
Maria R. Dekker, Alexander H. C. Hendriks, Noud Frielink, Petri J. C. M. Embregts
American Journal on Intellectual and Developmental Disabilities.2022; 127(6): 485. CrossRef - Coping strategies among children and adolescents: validity and reliability of the Arabic version of the Kidcope scale
Reham I. Abdelmageed, Yasmine I. Elhenawy, Dalia K. Zaafar, Asmaa W. Abdelaziz
Heliyon.2022; 8(1): e08706. CrossRef - Mental health of US undergraduate and graduate students before and during the COVID-19 pandemic: Differences across sociodemographic groups
Yuchen Liu, Patricia A. Frazier, Carolyn M. Porta, Katherine Lust
Psychiatry Research.2022; 309: 114428. CrossRef - Influence of caring for COVID‐19 patients on nurse's turnover, work satisfaction and quality of care
Mélanie Lavoie‐Tremblay, Céline Gélinas, Thalia Aubé, Eric Tchouaket, Dominique Tremblay, Marie‐Pierre Gagnon, José Côté
Journal of Nursing Management.2022; 30(1): 33. CrossRef - Psychometric Properties of the Bangla Version of the Stress and Anxiety to Viral Epidemics-6 Items Scale Among the General Population in Bangladesh
Oli Ahmed, Kazi Nur Hossain, Fatema Akhter Hiramoni, Rumana Ferdousi Siddique, Seockhoon Chung
Frontiers in Psychiatry.2022;[Epub] CrossRef - The conditional effect of family resilience on family quality of life during the Covid-19 pandemic
Tery Setiawan, Ria Wardani, Ellen Theresia
F1000Research.2022; 11: 1279. CrossRef - “I Can Learn How to Communicate Appropriately in This Language” Examining the Links between Language Mindsets and Understanding L2 Pragmatic Behaviours
Nourollah Zarrinabadi, Mohsen Rezazadeh, Salva Shirinbakhsh
Journal of Intercultural Communication Research.2022; 51(3): 309. CrossRef - Measuring Personality through Images: Validating a Forced-Choice Image-Based Assessment of the Big Five Personality Traits
Airlie Hilliard, Emre Kazim, Theodoros Bitsakis, Franziska Leutner
Journal of Intelligence.2022; 10(1): 12. CrossRef - Reliability and Validity of the Urdu Version of Psychosomatic Symptoms Scale in Pakistani Patients
S. Mudasser Shah, Muhammad Jahangir, Wei Xu, Yonggui Yuan
Frontiers in Psychology.2022;[Epub] CrossRef - Practical Considerations for Clinical Laboratories in Top-down Approach for Assessing the Measurement Uncertainty of Clinical Chemistry Analytes
Hyunjung Gu, Juhee Lee, Jinyoung Hong, Woochang Lee, Yeo-Min Yun, Sail Chun, Woo-In Lee, Won-Ki Min
Annals of Laboratory Medicine.2022; 42(6): 630. CrossRef - Validation and adaptation of the questionnaire on science motivation in the Russian context
Sergei P. Zhdanov, Alfia M. Ishmuradova, Valeria L. Zakharova, Svetlana V. Belous, Elena E. Grishnova
Eurasia Journal of Mathematics, Science and Technology Education.2022; 18(8): em2136. CrossRef - Effect of food cues on time perception: influence of calories and diet control
Quentin Hallez, Lisa Filippone, Rebecca Shankland
Scientific Reports.2022;[Epub] CrossRef - The role of servant leadership, self-efficacy, high performance work systems, and work engagement in increasing service-oriented behavior
Md Karim Rabiul, Ataul Karim Patwary, IM Panha
Journal of Hospitality Marketing & Management.2022; 31(4): 504. CrossRef - Detrimental educational practices deemed as culturally acceptable: Adultcentrism and Black Pedagogy in Italian primary schools
Eleonora Florio, Letizia Caso, Ilaria Castelli
Social Psychology of Education.2022; 25(1): 313. CrossRef - "A Romanian Version of the Experiences in Close Relationship Scale – Short Form (ECR-S) Measure of Adult Attachment"
Natalia CONSTANTINESCU, Fabien BACRO, Margareta DINCĂ
Journal of Evidence-Based Psychotherapies.2022; 22(1): 103. CrossRef - Telephone Interview for Cognitive Status (TICS): Italian adaptation, psychometrics and diagnostics
Edoardo Nicolò Aiello, Antonella Esposito, Ilaria Giannone, Lorenzo Diana, Ildebrando Appollonio, Nadia Bolognini
Neurological Sciences.2022; 43(5): 3071. CrossRef - Validation of the BFI-10-R: A New BFI Scale with Strong Structural and Construct Validity
Bryant M. Stone, Emily M. Bartholomay, Amanda B. Chamberlain
Journal of Psychopathology and Behavioral Assessment.2022; 44(4): 1064. CrossRef - The Impact of Aerobic Exercise on Mood Symptoms in Trauma-Exposed Young Adults: A Pilot Study
Allison L. Mizzi, Margaret C. McKinnon, Suzanna Becker
Frontiers in Behavioral Neuroscience.2022;[Epub] CrossRef - The effect of exercise on resilience, its mediators and moderators, in a general population during the UK COVID-19 pandemic in 2020: a cross-sectional online study
Molly Rose Lancaster, Patrick Callaghan
BMC Public Health.2022;[Epub] CrossRef - Validity and Reliability of the Dental Neglect Scale among Romanian Adults
Beatrice Adriana Balgiu, Ruxandra Sfeatcu, Christina Mihai, Roxana Romanița Ilici, Ioanina Parlatescu, Laura Tribus
Journal of Personalized Medicine.2022; 12(7): 1035. CrossRef - Perfectionism and Academic Adjustment among Undergraduates: The Coping Strategy as a Mediator
P.C. Siah, S.S. Ang, K.W. Tan, C.N. Phi, P.W. Pung
Psychological Science and Education.2022; 27(5): 57. CrossRef - The private rental housing market before and during the COVID-19 pandemic: A submarket analysis in Cracow, Poland
Mateusz Tomal, Marco Helbich
Environment and Planning B: Urban Analytics and City Science.2022; 49(6): 1646. CrossRef - Perceived usefulness of yoga to maintain well-being and in relation to COVID-19 cases among Hungarian yoga practitioners
Gusztáv J. TORNÓCZKY, Sándor RÓZSA, Henriett NAGY, Miklós BÁNHIDI
The Journal of Sports Medicine and Physical Fitness.2022;[Epub] CrossRef - The Relationship between Bicultural Identity Integration, Self-Esteem, Academic Resilience, Interaction Anxiousness, and School Belonging among University Students with Vocational Qualifications
Wenxin Chen, Yi Lin, Xiaoyan Yu, Wen Zheng, Shiyong Wu, Mingxi Huang, Wei Chen, Shuyi Zhou
International Journal of Environmental Research and Public Health.2022; 19(6): 3632. CrossRef - Working memory in intact modalities among individuals with sensory deprivation
Eyal Heled, Maayan Ohayon, Or Oshri
Heliyon.2022; 8(6): e09558. CrossRef - Predicting work performance and life satisfaction of nurses and physicians: The mediating role of social capital on self‐efficacy and psychological resilience
Hilal Kuşcu Karatepe, Hanife Tiryaki Şen, Emine Türkmen
Perspectives in Psychiatric Care.2022; 58(4): 2542. CrossRef - Leadership Styles, Psychological Factors, and Employee Commitment to Service Quality in the Hotel Industry
Md Karim Rabiul, Ataul Karim Patwary, Ahmad Edwin Mohamed, Harun-or Rashid
Journal of Quality Assurance in Hospitality & Tourism.2022; 23(4): 853. CrossRef - Dancing with service robots: The impacts of employee-robot collaboration on hotel employees’ job crafting
Yue Song, Mengying Zhang, Jiajing Hu, Xingping Cao
International Journal of Hospitality Management.2022; 103: 103220. CrossRef - Recurrent pain in school-aged children: a longitudinal study focusing on the relation to academic achievement
Susanne Ragnarsson, Klara Johansson, Erik Bergström, Gunnar Sjöberg, Anna-Karin Hurtig, Solveig Petersen
Pain.2022; 163(11): 2245. CrossRef - Prevalence and correlates of joint pain among Chinese breast cancer survivors receiving aromatase inhibitor treatment
Tao Wang, Yu-Yan Huang, Xian-Liang Liu, Alex Molassiotis, Li-Qun Yao, Si-Lin Zheng, Jing-Yu Tan, Hou-Qiang Huang
Supportive Care in Cancer.2022; 30(11): 9279. CrossRef - The General Public’s Perceptions of How the COVID-19 Pandemic Has Impacted the Elderly and Individuals with Intellectual Disabilities
Maria R. Dekker, Noud Frielink, Alexander H. C. Hendriks, Petri J. C. M. Embregts
International Journal of Environmental Research and Public Health.2022; 19(5): 2855. CrossRef - The Link between Parenting Behaviors and Emerging Adults’ Relationship Outcomes: The Mediating Role of Relational Entitlement
Octav-Sorin Candel
International Journal of Environmental Research and Public Health.2022; 19(2): 828. CrossRef - Gender Differences in Oral Health: Self-Reported Attitudes, Values, Behaviours and Literacy among Romanian Adults
Ruxandra Sfeatcu, Beatrice Adriana Balgiu, Christina Mihai, Ana Petre, Mihaela Pantea, Laura Tribus
Journal of Personalized Medicine.2022; 12(10): 1603. CrossRef - Relationships Between Physical Activity, Boredom Proneness, and Subjective Well-Being Among U.K. Adults During the COVID-19 Pandemic
Ashley McCurdy, Jodie A. Stearns, Ryan E. Rhodes, Debbie Hopkins, Kerry Mummery, John C. Spence
Journal of Sport & Exercise Psychology.2022; 44(3): 189. CrossRef - Adaptive behavior and psychiatric symptoms in university students with ASD: One-year longitudinal study
Gil Zukerman, Gili Yahav, Esther Ben-Itzchak
Psychiatry Research.2022; 315: 114701. CrossRef - Genomic selection for resistance to mammalian bark stripping and associated chemical compounds in radiata pine
Judith S Nantongo, Brad M Potts, Jaroslav Klápště, Natalie J Graham, Heidi S Dungey, Hugh Fitzgerald, Julianne M O'Reilly-Wapstra, T Pyhäjärvi
G3 Genes|Genomes|Genetics.2022;[Epub] CrossRef - Brain Injury Screening Tool (BIST): test–retest reliability in a community adult sample
Nusratnaaz Shaikh, Yelda Tokhi, Natalie Hardaker, Kevin Henshall, Katherine Forch, Kris Fernando, Doug King, Mark Fulcher, Sam Jewell, Renata Bastos-Gottgtroy, Patria Hume, Alice Theadom
BMJ Open.2022; 12(8): e057701. CrossRef - The psychometric properties of the Depression Anxiety Stress Scale-21 (DASS-21) Bangla version
Oli Ahmed, Rajib Ahmed Faisal, Sheikh MD ABU HENA Mostafa Alim, Tanima Sharker, Fatema Akhter Hiramoni
Acta Psychologica.2022; 223: 103509. CrossRef - Manusia dan lingkungan alam: Analisis faktor konfirmatori terhadap Nature Relatedness Scale Bahasa Indonesia
Bartolomeus Yofana Adiwena, Ratna Djuwita
Jurnal Psikologi Sosial.2022; 20(1): 57. CrossRef - The Italian Version of the ALS Depression Inventory-12
Debora Pain, Edoardo Nicolò Aiello, Marcello Gallucci, Massimo Miglioretti, Gabriele Mora
Frontiers in Neurology.2021;[Epub] CrossRef - Within-site drivers for soil nutrient variability in plantation forests: A case study from dry sub-humid New Zealand
Serajis Salekin, Mark Bloomberg, Justin Morgenroth, Dean F. Meason, Euan G. Mason
CATENA.2021; 200: 105149. CrossRef - Modelling age-friendly environment for social connectedness: a cross-sectional study
Lein Shi Ying, Lai Ming Ming, Lau Siok Hwa
F1000Research.2021; 10: 955. CrossRef - Predicting Family and Child Physical Activity across Six-Months of a Family-Based Intervention: An Application of Theory of Planned Behaviour, Planning and Habit
Ryan Rhodes, Alison Quinlan, Patti-Jean Naylor, Darren E.R. Warburton, Chris M. Blanchard
Journal of Sports Sciences.2021; 39(13): 1461. CrossRef - An Investigation into Knowledge of the Concept of Consumption: A Case of BA Students
Mehmet Necati CİZRELİOĞULLARI, Mehmet Veysi BABAYİĞİT, Özlem ALTUN
International Journal of Kurdish Studies.2021; 7(1): 22. CrossRef - Antecedents of the Attitudes Toward Singlehood Among Young Adults in Malaysia, Japan, and India
Chee-Seng Tan, Siew-May Cheng, Tomokazu Nakayama, Sanju George
Frontiers in Psychology.2021;[Epub] CrossRef - Stepping Up versus Stepping Out: On the outcomes and drivers of two alternative climate change adaptation strategies of smallholders
Md. Mofakkarul Islam, Md. Asaduzzaman Sarker, Md. Abdullah Al Mamun, Md. Mamun-ur-Rashid, Debashis Roy
World Development.2021; 148: 105671. CrossRef - Revised Short Screening Version of the Profile of Mood States (POMS) From the German General Population
Katja Petrowski, Cornelia Albani, Markus Zenger, Elmar Brähler, Bjarne Schmalbach
Frontiers in Psychology.2021;[Epub] CrossRef - Motivational Mechanisms Underlying Second Language Achievement: A Regulatory Focus Perspective
Mostafa Papi, Gholam Hassan Khajavy
Language Learning.2021; 71(2): 537. CrossRef - The Relationship Between Prosocial and Antisocial Behaviors and Personality Traits in Team Athletes
Selman CUTUK, Zülbiye KAÇAY, Zeynep AKKUŞ ÇUTUK
Sakarya University Journal of Education.2021; 11(1): 182. CrossRef - Variation in chemistry instructors’ evaluations of student written responses and its impact on grading
Michelle Herridge, Jenna Tashiro, Vicente Talanquer
Chemistry Education Research and Practice.2021; 22(4): 948. CrossRef - Cone beam computed tomography analysis of accessory canals of the canalis sinuosus: A prevalent but often overlooked anatomical variation in the anterior maxilla
Tiantian Shan, Yang Qu, Xiangya Huang, Lisha Gu
The Journal of Prosthetic Dentistry.2021; 126(4): 560. CrossRef - ASSESSMENT OF THE AWARENESS LEVEL OF RADIATION PROTECTION AMONG RADIOGRAPHERS WORKING IN THE MEDICAL IMAGING WARDS OF THE HOSPITALS IN ZANJAN, IRAN
Parastoo Moghimi, Khadijeh Hajimiri, Franak Saghatchi, Hamed Rezaeejam
Radiation Protection Dosimetry.2021; 194(2-3): 97. CrossRef - Intrafamily relations and resilience as protectors against depressive symptoms in Mexican high school students
Héctor Rubén Bravo-Andrade
Salud mental.2021; 44(3): 127. CrossRef - Loneliness, Emotion Dysregulation, and Internalizing Symptoms During Coronavirus Disease 2019: A Structural Equation Modeling Approach
Patrizia Velotti, Guyonne Rogier, Sara Beomonte Zobel, Rosetta Castellano, Renata Tambelli
Frontiers in Psychiatry.2021;[Epub] CrossRef - Psychometric properties of the Raven's Standard Progressive Matrices in a Portuguese sample
Inês Queiroz-Garcia, Helena Espirito Santo, Catarina Pires
Revista Portuguesa de Investigação Comportamental e Social.2021; 7(1): 84. CrossRef - Psychometric properties of the Generalized Anxiety Disorder-7 Scale in Ethiopian university students
Md. Dilshad Manzar, Mohammed Salahuddin, Ahmad Alghadir, Shahnawaz Anwer, Sony Peter, Ahmed S. Bahammam, Seithikurippu R. Pandi-Perumal
Bulletin of the Menninger Clinic.2021; 85(4): 405. CrossRef - Nursing educators’ and undergraduate nursing students’ beliefs and perceptions on evidence-based practice, evidence implementation, organizational readiness and culture: An exploratory cross-sectional study
Daniela Cardoso, Manuel Rodrigues, Rui Pereira, Vítor Parola, Adriana Coelho, Lucimare Ferraz, Maria Lucília Cardoso, Mary-Anne Ramis, João Apóstolo
Nurse Education in Practice.2021; 54: 103122. CrossRef - Cross-cultural translation, adaptation, and validation of the Amharic version pain self-efficacy questionnaire in people with low back pain in Ethiopia
Mulugeta Bayisa Chala, Catherine Donnelly, Yemataw Wondie, Setareh Ghahari, Jordan Miller
BMC Musculoskeletal Disorders.2021;[Epub] CrossRef - Addictive internet behaviors: The role of trait emotional intelligence, self‐esteem, age, and gender
Cristina Sechi, Giorgia Loi, Cristina Cabras
Scandinavian Journal of Psychology.2021; 62(3): 409. CrossRef - The Development of a Measure to Assess Social Reactions to Self-Injury Disclosure
Brooke A. Ammerman, Michael S. McCloskey
Assessment.2021; 28(1): 225. CrossRef - Short report and initial evaluation of the factor structure of the Lancaster and Northgate Trauma Scales (LANTS)
Sarah Wigham, Chris Hatton, John L. Taylor
Research in Developmental Disabilities.2021; 112: 103914. CrossRef - Development and validation of a general legal moral disengagement scale
Jacqueline M. Kirshenbaum, Monica K. Miller, Tatyana Kaplan, Robert J. Cramer, Sarah A. Trescher, Tess M. S. Neal
Psychology, Crime & Law.2021; 27(8): 751. CrossRef - Knowledge, attitudes, and practices towards dengue prevention among primary school children with and without experience of previous dengue infection in southern Thailand
Charuai Suwanbamrung, Bussarawadee Saengsuwan, Thamonwan Sangmanee, Napaporn Thrikaew, Poungpen Srimoung, Sarunya Maneerattanasak
One Health.2021; 13: 100275. CrossRef - The Impact of Moral-Based Appraisals on Psychological Outcomes in Response to Analogue Trauma: An Experimental Paradigm of Moral Injury
Joel Hoffman, Angela Nickerson
Cognitive Therapy and Research.2021; 45(3): 494. CrossRef - Cortical Thickness in bilingual and monolingual children: Relationships to language use and language skill
Kelly A. Vaughn, My V.H. Nguyen, Juliana Ronderos, Arturo E. Hernandez
NeuroImage.2021; 243: 118560. CrossRef - Sensitivity to Change and Responsiveness of the Original and the Shortened Version of the Community Balance and Mobility Scale for Young Seniors
Katharina Gordt, Corinna Nerz, A. Stefanie Mikolaizak, Kristin Taraldsen, Mirjam Pijnappels, Jorunn L. Helbostad, Beatrix Vereijken, Clemens Becker, Michael Schwenk
Archives of Physical Medicine and Rehabilitation.2021; 102(11): 2102. CrossRef - The Bullshitting Frequency Scale: Development and psychometric properties
Shane Littrell, Evan F. Risko, Jonathan A. Fugelsang
British Journal of Social Psychology.2021; 60(1): 248. CrossRef - Knowledge, attitude, and use of protective measures against COVID-19 among nurses: a questionnaire-based multicenter cross-sectional study
Ramzi Shawahna
BMC Nursing.2021;[Epub] CrossRef - Early Improvement in Patient-Reported Outcome Scores After Operative Treatment of Osteochondritis Dissecans of the Humeral Capitellum
Mitchel R. Obey, Charles A. Goldfarb, J. Sam Broughton, Sandra S. Gebhart, Matthew V. Smith
The Journal of Hand Surgery.2021; 46(12): 1120.e1. CrossRef - Construct validation of leaders’ motivating language in the context of the hotel industries of Bangladesh and Malaysia
Md Karim Rabiul, Tan Fee Yean, Ataul Karim Patwary, Ahmad Edwin Mohamed, Haim Hilman
International Journal of Contemporary Hospitality Management.2021; 33(8): 2695. CrossRef - Depression predicts emotion acceptance beliefs in early adolescence: A longitudinal investigation
Lauren J. Harvey, Fiona A. White, Claire E. McAulay
British Journal of Clinical Psychology.2021; 60(4): 513. CrossRef - International study to develop the WOUND‐Q patient‐reported outcome measure for all types of chronic wounds
Anne F. Klassen, Emiel L. W. G. van Haren, Tert C. van Alphen, Stefan Cano, Karen M. Cross, Anne‐Margreet van Dishoeck, Kenneth L. Fan, Maarten Michael Hoogbergen, Dennis Orgill, Lotte Poulsen, Jens Ahm Sørensen, Lee Squitieri, Elena Tsangaris, Dalibor Va
International Wound Journal.2021; 18(4): 487. CrossRef - Understanding confidentiality breach in adolescent mental health sessions: an integrated model of culture and parenting
Elvin Yao, Yuhua Li, Chunhui Wang, Jianwen Hui
Ethics & Behavior.2021; 31(4): 245. CrossRef - Hunger games: Associations between core eating disorder symptoms and responses to rejection by peers during competition
Sarah E. Schell, Iulia Banica, Anna Weinberg, Sarah E. Racine
International Journal of Eating Disorders.2021; 54(5): 802. CrossRef - Computation of sales performance score and key cross-functional factors: a performance dynamics in IT/ITES
Sumit Saha, Subhasree Kar
American Journal of Business.2021; 36(1): 3. CrossRef - Measuring the effectiveness of psychoeducation on adherence, depression, anxiety and stress among patients with diagnosis of schizophrenia. a control trial
Apostolia Alizioti, Georgios Lyrakos
Current Psychology.2021; 40(8): 3639. CrossRef - Tumor diameter as a predictor of lymph node involvement in endometrioid type endometrial adenocarcinomas
Serkan Akış, Canan Kabaca, Esra Keleş, Uğur Kemal Öztürk, Eser Özyürek, Murat Api, Handan Çetiner, Evrim Bostancı
Journal of Obstetrics and Gynaecology Research.2021; 47(11): 3968. CrossRef - Influence of Resilience and Optimism on Distress and Intention to Self-Isolate: Contrasting Lower and Higher COVID-19 Illness Risk Samples From an Extended Health Belief Model
Sergio Cervera-Torres, Susana Ruiz-Fernández, Hendrik Godbersen, Lena Massó, David Martínez-Rubio, Sheila Pintado-Cucarella, Rosa M. Baños
Frontiers in Psychology.2021;[Epub] CrossRef - Sustainable Consumer Behavior in Purchasing, Using and Disposing of Clothes
Mirella Soyer, Koen Dittrich
Sustainability.2021; 13(15): 8333. CrossRef - Distance education amid a pandemic: Which psycho‐demographic variables affect students in higher education?
İdris Göksu, Naif Ergün, Zafer Özkan, Halis Sakız
Journal of Computer Assisted Learning.2021; 37(6): 1539. CrossRef - High Olfactory Receptor-Rich 11q11 Copy Number in Girls and African American Children
Megan Phillips, Vaithinathan Selvaraju, Anna Fouty, Jeganathan Ramesh Babu, Maninder Sandey, Thangiah Geetha
Genes.2021; 12(12): 1943. CrossRef - Latent profile analysis of blood marker phenotypes and their relationships with clinical pain and interference reports in people with acute musculoskeletal trauma
Joshua Y. Lee, David M. Walton
Canadian Journal of Pain.2021; 5(1): 30. CrossRef - Autistic Traits and Attention-Deficit Hyperactivity Disorder Symptoms Associated With Greater Pain Interference and Depression, and Reduced Health-Related Quality of Life in Children With Chronic Pain
Camilla Wiwe Lipsker, Tatja Hirvikoski, Leonie J. T. Balter, Sven Bölte, Mats Lekander, Linda Holmström, Rikard K. Wicksell
Frontiers in Neuroscience.2021;[Epub] CrossRef - Dijital İletişim Mecralarında Dezavantajlı Türlerin Sesi Olmak: Hayvanseverlerin Siyasal Katılım Faaliyetleri Üzerinde Empati ve Grup Bilincinin Rolü
Şakir GÜLER
İletişim Kuram ve Araştırma Dergisi.2021; 2021(56): 142. CrossRef - Influence of Leader Mindfulness on the Emotional Exhaustion of University Teachers: Resources Crossover Effect
Beini Liu, Zehui Zhang, Qiang Lu
Frontiers in Psychology.2021;[Epub] CrossRef - The vulnerability of insecure minds: The mediating role of mentalization in the relationship between attachment styles and psychopathology
Gianluca Santoro, Laura Rosa Midolo, Antonino Costanzo, Adriano Schimmenti
Bulletin of the Menninger Clinic.2021; 85(4): 358. CrossRef - Evaluation of Usability of the Tiger Full Foot 3D Scanner for the Measurements of Basic Foot Dimensions in Clinical Practice
Ondřej Laštovička, Roman Cuberek, Miroslav Janura, Tomáš Klein
Journal of the American Podiatric Medical Association.2021;[Epub] CrossRef - The Relationship between the Therapeutic Alliance and Suicidal Experiences in People with Psychosis Receiving Therapy
Charlotte Huggett, Patricia Gooding, Gillian Haddock, Daniel Pratt
International Journal of Environmental Research and Public Health.2021; 18(20): 10706. CrossRef - Determinants of digital commerce repeat-purchase behaviour in South Africa: A rural citizen perspective
Vusani Netshirando, Willard Munyoka, Armstrong Kadyamatimba
African Journal of Science, Technology, Innovation and Development.2021; 13(6): 701. CrossRef - Theory of Mind Ability and Socioeconomic Status, a Study of Street-Connected Children and Adolescents in Ecuador
Graham Pluck
Psych.2021; 3(2): 72. CrossRef - An extension of the Thermodynamics Conceptual Reasoning Inventory (TCRI): measuring undergraduate students’ understanding of introductory thermodynamics concepts
Carla M. Firetto, Peggy N. Van Meter, Alexa M. Kottmeyer, Stephen R. Turns, Thomas A. Litzinger
International Journal of Science Education.2021; 43(15): 2555. CrossRef - The Roles of Self-Concealment and Perceived Racial and Ethnic Discrimination in General Psychological Distress among Racial and Ethnic Minority College Students in the United States
Akihiko Masuda, G. E. Kawika Allen, Charles Liu, Erin C. Tully
International Journal for the Advancement of Counselling.2021; 43(4): 472. CrossRef - Smoking-Cessation Acceptance Via Mobile Health and Quick Response Code Technologies: Empirical Evidence of a Pilot Study from China and Pakistan
Rahib Ali, Ziqiong Zhang, Muhammad Bux Soomro
Current Psychology.2021; 40(12): 6085. CrossRef - Spirituality as a Mediator Between Depressive Symptoms and Subjective Well-being in Older Adults
Mária Sováriová Soósová, Vladimíra Timková, Lucia Dimunová, Boris Mauer
Clinical Nursing Research.2021; 30(5): 707. CrossRef - Psychological Resilience of Healthcare Professionals During COVID-19 Pandemic
Faruk Bozdağ, Naif Ergün
Psychological Reports.2021; 124(6): 2567. CrossRef - Same room - different windows? A systematic review and meta-analysis of the relationship between self-report and neuropsychological tests of cognitive flexibility in healthy adults
Caitlin A. Howlett, Michael A. Wewege, Carolyn Berryman, Annika Oldach, Elizabeth Jennings, Emily Moore, Emma L. Karran, Kimberley Szeto, Leander Pronk, Stephanie Miles, G. Lorimer Moseley
Clinical Psychology Review.2021; 88: 102061. CrossRef - Investigation of the Impact of Deicer Materials on Thermodynamic Parameters and Its Relationship with Moisture Susceptibility in Modified Asphalt Mixtures by Carbon Nanotube
Vahid Najafi Moghaddam Gilani, Seyed Mohsen Hosseinian, Daniel Safari, Mojtaba Bagheri Movahhed
Arabian Journal for Science and Engineering.2021; 46(5): 4489. CrossRef - Immune challenges increase network centrality in a queenless ant
Giacomo Alciatore, Line V. Ugelvig, Erik Frank, Jérémie Bidaux, Asaf Gal, Thomas Schmitt, Daniel J. C. Kronauer, Yuko Ulrich
Proceedings of the Royal Society B: Biological Sciences.2021;[Epub] CrossRef - Determinants of Fitness App Usage and Moderating Impacts of Education-, Motivation-, and Gamification-Related App Features on Physical Activity Intentions: Cross-sectional Survey Study
Yanxiang Yang, Joerg Koenigstorfer
Journal of Medical Internet Research.2021; 23(7): e26063. CrossRef - Risky Casual Sex and Posttraumatic Stress in College Females: An Examination of Assault History, Self-Esteem, and Social Support
Seigie Kennedy, Christina Balderrama-Durbin
Violence Against Women.2021; 27(15-16): 3074. CrossRef - Development and Psychometric Validation of BREAST-Q Scales Measuring Cancer Worry, Fatigue, and Impact on Work
Anne F. Klassen, Manraj N. Kaur, Elena Tsangaris, Claire E. E. de Vries, Louise Bordeleau, Toni Zhong, Stefan J. Cano, Trisia Breitkopf, Andrea L. Pusic
Annals of Surgical Oncology.2021; 28(12): 7410. CrossRef - Poor Mental Health in Caregivers of Children with Attention-Deficit/Hyperactivity Disorder and Its Relationships with Caregivers’ Difficulties in Managing the Children’s Behaviors and Worsened Psychological Symptoms during the COVID-19 Pandemic
Hui-Wen Tseng, Ching-Shu Tsai, Yu-Min Chen, Ray C. Hsiao, Fan-Hao Chou, Cheng-Fang Yen
International Journal of Environmental Research and Public Health.2021; 18(18): 9745. CrossRef - Association Between Communicative Participation and Psychosocial Factors in Patients With Voice Disorders
Viann N. Nguyen-Feng, Alexa Asplund, Patricia A. Frazier, Stephanie Misono
JAMA Otolaryngology–Head & Neck Surgery.2021; 147(3): 245. CrossRef - The Relationship between Adolescent's Free Verses Enforced Decision to Enroll in an out-of- Home Boarding School and Later Well-being
Rachel Lev-Wiesel, Rotem Dar, Yael Paz, Anat Arazi-Aviram, Efrat Yosef, Gali Sonego, Susan Weinger, Hadas Doron, Vered Shenaar-Golan
European Journal of Educational Research.2021; volume-10-(volume-10-): 1. CrossRef - Healthcare utilization and costs associated with persistent post-concussive symptoms
Sabrina Agnihotri, Melanie Penner, Kylie D. Mallory, Lucy Xie, Andrea Hickling, Nicholas Joachimides, Elaine Widgett, Shannon E. Scratch
Brain Injury.2021; 35(11): 1382. CrossRef - Gender as a Moderator of the Relationship Between Parental Anxiety and Adolescent Anxiety and Depression
Rachel M. Ranney, Evelyn Behar, Katherine M. Zinsser
Journal of Child and Family Studies.2021; 30(5): 1247. CrossRef - Musical aptitude, working memory, general intelligence and plurilingualism: When adults learn to read fluently in a foreign language
M.C Fonseca-Mora, Francisco H. Machancoses, Olena Gryb, Susanne Reiterer, Abbas Pourhosein Gilakjani
Cogent Education.2021;[Epub] CrossRef - Development and Psychometric Validation of the BREAST-Q Sensation Module for Women Undergoing Post-Mastectomy Breast Reconstruction
Elena Tsangaris, Anne F. Klassen, Manraj N. Kaur, Sophocles Voineskos, Louise Bordeleau, Toni Zhong, Justin Broyles, Andrea L. Pusic
Annals of Surgical Oncology.2021; 28(12): 7842. CrossRef - Self-esteem and perceived social competence protect adolescent students against ostracism and loneliness
Halis Sakız, Abdullah Mert, Hakan Sarıçam
Journal of Psychologists and Counsellors in Schools.2021; 31(1): 94. CrossRef - The Role of Need for Closure and Need for Cognition in Writing-Specific Psychological Factors
Mohsen Rezazadeh, Nourollah Zarrinabadi
Discourse Processes.2021; 58(10): 869. CrossRef - Development of the Oral Health Literacy Profile (OHLP)—Psychometric properties of the oral health and dental health system knowledge scales
Kristin Spinler, Richelle Valdez, Ghazal Aarabi, Demet Dingoyan, Daniel Ralph Reissmann, Guido Heydecke, Olaf von dem Knesebeck, Christopher Kofahl
Community Dentistry and Oral Epidemiology.2021; 49(6): 609. CrossRef - Relating outdoor play to sedentary behavior and physical activity in youth - results from a cohort study
Carina Nigg, Claudia Niessner, Claudio R. Nigg, Doris Oriwol, Steffen C. E. Schmidt, Alexander Woll
BMC Public Health.2021;[Epub] CrossRef - Xenophobia in the Time of a Pandemic: Social Media Use, Stereotypes, and Prejudice against Immigrants during the COVID-19 Crisis
Saifuddin Ahmed, Vivian Hsueh Hua Chen, Arul Indrasen Chib
International Journal of Public Opinion Research.2021; 33(3): 637. CrossRef - Translational cultural adaptation and psychometric study of the Persian version of pediatric inventory for parents
Sedigheh Khanjari, Fereshteh Javaheri Tehrani, Shabnam Shariat Panahi, Ahmad Saidee
Journal of Education and Health Promotion.2021;[Epub] CrossRef - Nutrition Supports Deconstructed and Disrupted: An Evaluation of a Multilevel School-Based Intervention during the Time of COVID
Rachael D. Dombrowski, Bree Bode, Kathryn A. G. Knoff, James Mallare, E. Whitney G. Moore, Noel Kulik
International Journal of Environmental Research and Public Health.2021; 18(21): 11006. CrossRef - Experimental investigation and multi-objective optimization of fracture properties of asphalt mixtures containing nano-calcium carbonate
Ahmad Ghasemzadeh Mahani, Payam Bazoobandi, Seyed Mohsen Hosseinian, Hassan Ziari
Construction and Building Materials.2021; 285: 122876. CrossRef - Self-Control at Meals in Order Not to Gain Weight and Its Relationship with Food Cravings in Low-Carb Dieters
Jônatas Oliveira, Táki Athanássios Cordás
Obesities.2021; 1(3): 200. CrossRef - The effects of psychodrama groups on feelings of inferiority, flourishing, and self-compassion in research assistants
Gamze Ülker Tümlü, Bircan Kırlangıç Şimşek
The Arts in Psychotherapy.2021; 73: 101763. CrossRef - Effect of leader mindfulness on hindrance stress in nurses: The social mindfulness information processing path
Beini Liu, Haizhu Zhao, Qiang Lu
Journal of Advanced Nursing.2021; 77(11): 4414. CrossRef - Predictive factors of quality of life among the elderly in Iran: Application of Andersen's behavioral model
Soghra Nazari, Koorosh Kamali, Khadijeh Hajimiri
Journal of Education and Health Promotion.2021;[Epub] CrossRef - Translation of the Fear of COVID-19 Scale into French-Canadian and English-Canadian and Validation in the Nursing Staff of Quebec
Céline Gélinas, Christine Maheu, Mélanie Lavoie-Tremblay, Mélissa Richard-Lalonde, Maria Cecilia Gallani, Émilie Gosselin, Maude Hébert, Eric Tchouaket Nguemeleu, José Côté
Science of Nursing and Health Practices.2021; 4(1): 1. CrossRef - Coping associated with compulsive buying tendency
Lee M. Lawrence, Bradley Elphinstone
Stress and Health.2021; 37(2): 263. CrossRef - Öğretmenler İçin Yenilikçi Pedagoji Uygulamaları Ölçeği: Geçerlik ve Güvenirlik Çalışması
Sedef SÜER, Behçet ORAL
Mersin Üniversitesi Eğitim Fakültesi Dergisi.2021; 17(1): 132. CrossRef - Could Modifying the Skin Microbiome, Diet, and Lifestyle Help with the Adverse Skin Effects after Stopping Long-Term Topical Steroid Use?
Christopher Wallen-Russell, Anja Gijsberts-Veens, Samuel Wallen-Russell
Allergies.2021; 2(1): 1. CrossRef - The impact of student perception surveys on teachers’ practice: Teacher resistance and struggle in student voice-based assessment initiatives of effective teaching
Ilana Finefter-Rosenbluh, Tracii Ryan, Melissa Barnes
Teaching and Teacher Education.2021; 106: 103436. CrossRef - Private health insurance customer satisfaction. A consumer behavior exploratory study based on structural equation modeling
Adina Rotileanu, Lucian-Florin Onişor
Proceedings of the International Conference on Business Excellence.2021; 15(1): 650. CrossRef - Quality of life and its association with psychiatric disorders in outpatients with trauma history in a tertiary hospital in Kathmandu, Nepal: a cross-sectional study
Saraswati Dhungana, Rishav Koirala, Saroj Prasad Ojha, Suraj Bahadur Thapa
BMC Psychiatry.2021;[Epub] CrossRef - Therapist Attachment and the Working Alliance: The Moderating Effect of Emotional Regulation
Desireé Ruiz-Aranda, Sara Cardoso-Álvarez, Javier Fenollar-Cortés
Frontiers in Psychology.2021;[Epub] CrossRef - POZİTİF PSİKOLOJİ TEMELLİ PERMA GRUPLA PSİKOLOJİK DANIŞMA UYGULAMASININ ÜNİVERSİTE ÖĞRENCİLERİNİN İYİ OLUŞLARINA ETKİSİ: BİR PİLOT ÇALIŞMA
İbrahim DEMİRCİ
Abant İzzet Baysal Üniversitesi Eğitim Fakültesi Dergisi.2021; 21(2): 453. CrossRef - Effects of crude oil prices on copper and maize prices
Byrne Kaulu
Future Business Journal.2021;[Epub] CrossRef - The Montreal Cognitive Assessment (MoCA): updated norms and psychometric insights into adaptive testing from healthy individuals in Northern Italy
Edoardo Nicolò Aiello, Chiara Gramegna, Antonella Esposito, Valentina Gazzaniga, Stefano Zago, Teresa Difonzo, Ottavia Maddaluno, Ildebrando Appollonio, Nadia Bolognini
Aging Clinical and Experimental Research.2021; 34(2): 375. CrossRef - The Role of Coping Behavior in Healthcare Workers' Distress and Somatization During the COVID-19 Pandemic
Erik Franck, Filip Haegdorens, Eva Goossens, Yannic van Gils, Michael Portzky, Francis Somville, Majed Abuawad, Stijn Slootmans, Peter Van Bogaert
Frontiers in Psychology.2021;[Epub] CrossRef - Impact of Supplemental Nutrition Assistance Program Benefit Reduction or Loss on Food-at-Home Acquisitions and Community Food Program Use
Namrata Sanjeevi
International Journal of Environmental Research and Public Health.2021; 18(22): 12004. CrossRef - Travelers’ motivations to adopt augmented reality (AR) applications in a tourism destination
Hyejo Hailey Shin, Miyoung Jeong
Journal of Hospitality and Tourism Technology.2021; 12(2): 389. CrossRef - Gender Differences in Psychological Impact of the Confinement During the COVID-19 Outbreak in Spain: A Longitudinal Study
Javier Fenollar-Cortés, Óliver Jiménez, Antonio Ruiz-García, Davinia M. Resurrección
Frontiers in Psychology.2021;[Epub] CrossRef - Validation of the professional identity questionnaire among medical students
Daan Toben, Marianne Mak-van der Vossen, Anouk Wouters, Rashmi A. Kusurkar
BMC Medical Education.2021;[Epub] CrossRef - Socio-interactive practices and personality within an EFL online learning environments
Asma Almusharraf, Norah Almusharraf
Education and Information Technologies.2021; 26(4): 3947. CrossRef - Which Domains of Social Support Better Predict Quality of Life of Women with Breast Cancer? A Cross-Sectional Study
Hadi Zamanian, Mona Daryaafzoon, Sahar Foroozanfar, Zinat Fakhri, Tina Jalali, Amene Ghotbi, Mohammadali Amini-Tehrani
Asia-Pacific Journal of Oncology Nursing.2021; 8(2): 211. CrossRef - Mediating Role of Sense of Coherence in the Relationship of Perceived Stress with Fatigue and Pain in Multiple Sclerosis Patients
Samira Zarrabi-Ajami, Hadi Zamanian, Adis Kraskian Mujembari, Sara Pashang
Qom Univ Med Sci J.2021; 14(11): 38. CrossRef - Linking Health Literacy to Self-Care in Hypertensive Patients with Physical Disabilities: A Path Analysis Using a Multi-Mediation Model
Hye Jin Nam, Ju Young Yoon
International Journal of Environmental Research and Public Health.2021; 18(7): 3363. CrossRef - Effects of brief stress management interventions on distress and leukocyte nuclear factor kappa B expression during primary treatment for breast cancer: A randomized trial
Alain Diaz, Chloe J. Taub, Marc E. Lippman, Michael H. Antoni, Bonnie B. Blomberg
Psychoneuroendocrinology.2021; 126: 105163. CrossRef - Creative Adaptability: Conceptual Framework, Measurement, and Outcomes in Times of Crisis
Hod Orkibi
Frontiers in Psychology.2021;[Epub] CrossRef - Prevalence and correlates of unmet palliative care needs in dyads of Chinese patients with advanced cancer and their informal caregivers: a cross-sectional survey
Tao Wang, Alex Molassiotis, Jing-Yu Tan, Betty Pui Man Chung, Hou-Qiang Huang
Supportive Care in Cancer.2021; 29(3): 1683. CrossRef - Exploring Resilience in Undergraduate and Early Career Paramedics
Katie Leigh Mann, Shannon Delport, Robert Stanton, Danielle Every
Australasian Journal of Paramedicine.2021; 18: 1. CrossRef - What Happens after Hospital Discharge? Deficiencies in Medication Management Encountered by Geriatric Patients with Polypharmacy
Laura Mortelmans, Elyne De Baetselier, Eva Goossens, Tinne Dilles
International Journal of Environmental Research and Public Health.2021; 18(13): 7031. CrossRef - Relationships between Heavy Metals and Their Connection to Amorphous and Total Iron in a Frequently Subsampled Clay Pit Core Sample
Josip Jurković, Senad Murtić, Fejzo Bašić, Teofil Gavrić, Emina Sijahović, Sabrija Čadro
ACS Earth and Space Chemistry.2021; 5(7): 1726. CrossRef - Association between Participation Activities, Pain Severity, and Psychological Distress in Old Age: A Population-Based Study of Swedish Older Adults
Elena Dragioti, Björn Gerdle, Lars-Åke Levin, Lars Bernfort, Huan-Ji Dong
International Journal of Environmental Research and Public Health.2021; 18(6): 2795. CrossRef - The Impact of Interactivity on User Satisfaction in Digital Social Reading: Social Presence as a Mediator
Wu Li, Yuanyi Mao, Liuning Zhou
International Journal of Human–Computer Interaction.2021; 37(17): 1636. CrossRef - Impact of adding palatal rugae to complete dentures on patient satisfaction and oral health–related quality of life: A randomized crossover clinical trial
Motasum Abu-Awwad, Nadia Ereifej, Mais Al-Hattab, Dima Abu Baker, Haralampos Petridis
The Journal of Prosthetic Dentistry.2021; 126(5): 646. CrossRef - Tour leader likeability and tourist citizenship behaviours: mediating effect of perceived value
Sheng-Hshiung Tsaur, Tsung-Lin Yang, Cheng-Hsien Tsai
Current Issues in Tourism.2021; 24(18): 2628. CrossRef - Do religious beliefs influence concerns for animal welfare? the role of religious orientation and ethical ideologies in attitudes toward animal protection amongst Muslim teachers and school staff in East Java, Indonesia
Dexon Pasaribu, Pim Martens, Bagus Takwin, Anima Nanda
PLOS ONE.2021; 16(7): e0254880. CrossRef - Validation of the COVID-19 Transmission Misinformation Scale and Conditional Indirect Negative Effects on Wearing a Mask in Public
Stephen Bok, Daniel E. Martin, Erik Acosta, Maria Lee, James Shum
International Journal of Environmental Research and Public Health.2021; 18(21): 11319. CrossRef - The role of fragrance and self-esteem in perception of body odors and impressions of others
Ilja Croijmans, Daniel Beetsma, Henk Aarts, Ilse Gortemaker, Monique Smeets, Maria Serena Panasiti
PLOS ONE.2021; 16(11): e0258773. CrossRef - Hybrid Model for Assessing the Influence of Safety Management Practices on Labor Productivity in Multistory Building Projects
Argaw Tarekegn Gurmu
Journal of Construction Engineering and Management.2021;[Epub] CrossRef - Öğretmenlerde Çözüm Odaklı Düşünme İle Mutluluk İlişkisinde Sürekli Umut ve Yaşam Doyumunun Aracı Rolü
Fuat AYDOĞDU
Psikiyatride Güncel Yaklaşımlar.2021; 13(Ek 1): 337. CrossRef - Significant association of nicotine reinforcement and cue reactivity: a translational study in humans and rats
Kevin Butler, Benoît Forget, Stephen J. Heishman, Bernard Le Foll
Behavioural Pharmacology.2021; 32(2&3): 212. CrossRef - Significant Life Events and Career Sustainability: A Three-Wave Study
Shagini Udayar, Leandro Ivan Canzio, Ieva Urbanaviciute, Jonas Masdonati, Jérôme Rossier
Sustainability.2021; 13(23): 13129. CrossRef - Mother-child interactions during feeding: A study on maternal sensitivity in dyads with underweight and normal weight toddlers
Giulia Ballarotto, Luca Cerniglia, Laura Bozicevic, Silvia Cimino, Renata Tambelli
Appetite.2021; 166: 105438. CrossRef - Public stigmatisation of people with intellectual disabilities: a mixed-method population survey into stereotypes and their relationship with familiarity and discrimination
Hannah A. Pelleboer-Gunnink, Jaap van Weeghel, Petri J. C. M. Embregts
Disability and Rehabilitation.2021; 43(4): 489. CrossRef - Prognostic impact of iron deficiency in acute coronary syndromes
Carina Silva, Juliana Martins, Isabel Campos, Carina Arantes, Carlos Galvão Braga, Nuno Salomé, António Gaspar, Pedro Azevedo, Miguel Álvares Pereira, Jorge Marques, Catarina Vieira
Revista Portuguesa de Cardiologia (English Edition).2021; 40(8): 525. CrossRef - Improving malaria preventive practices and pregnancy outcomes through a health education intervention: A randomized controlled trial
Ahmed Dahiru Balami, Salmiah Md. Said, Nor Afiah Mohd Zulkefli, Bachok Norsa’adah, Bala Audu
Malaria Journal.2021;[Epub] CrossRef - Travel behaviour after the pandemic: the case of Bulgaria
Maya Ivanova, Ivan Krasimirov Ivanov, Stanislav Ivanov
Anatolia.2021; 32(1): 1. CrossRef - Comparison of the Psychometric Properties of Three Fatigue Scales in Persian-Speaking Patients with Multiple Sclerosis
Shabnam Behrangrad, Amin Kordi Yoosefinejad
International Journal of MS Care.2021; 23(1): 8. CrossRef - Psychometric Properties of the German Version of the Self-Regulation of Eating Behavior Questionnaire
Ileana Schmalbach, Bjarne Schmalbach, Markus Zenger, Katja Petrowski, Manfred Beutel, Anja Hilbert, Elmar Brähler
Frontiers in Psychology.2021;[Epub] CrossRef - Organizational Trust Perception and Innovative Behaviours of Teachers
Selcuk Demir
European Journal of Educational Management.2021; volume-4-2(volume-4-i): 25. CrossRef - Intensive Care Nurses’ Knowledge, Attitude, and Practice of Pressure Injury Prevention in China: A Cross-Sectional Study
Li Hu, Wipa Sae-Sia, Luppana Kitrungrote
Risk Management and Healthcare Policy.2021; Volume 14: 4257. CrossRef - Validation of corporate environmental citizenship measurement in Malaysia
Lee Chin Tay, Fee Yean Tan, Khulida Kirana Yahya, Amran Rasli
European Business Review.2021; 33(2): 345. CrossRef - Understanding the relationship between parenting style and chronic pain in adolescents: a structural equation modelling approach
Maryam Shaygan, Pardis Bostanian, Mina Zarmehr, Hamidreza Hassanipour, Maryam Mollaie
BMC Psychology.2021;[Epub] CrossRef - Black Beauty: Womanist Consciousness as a Protective Factor in Black Women’s Body Image Satisfaction
Speshál Walker Gautier
Journal of Black Psychology.2021; 47(8): 631. CrossRef - Applying Mamdani’s method to categorize mathematical literacy of public middle school students in Kupang
D W Fointuna
Journal of Physics: Conference Series.2021; 1957(1): 012009. CrossRef - Predicting early reading fluency based on preschool measures of low‐level visual temporal processing: A possible mediation by high‐level visual temporal processing skills
Ningyu Liu, Jing Zhao, Chen Huang, Xiaopei Xing, Shan Lu, Zhengyan Wang
Infant and Child Development.2021;[Epub] CrossRef - Effect of the radiation balance on warming occurrence over West Africa
O.S. Ojo, I. Emmanuel, B. Adeyemi, E.O. Ogolo
Scientific African.2021; 11: e00700. CrossRef - An Analysis of the Influencing Factors of Study Engagement and Its Enlightenment to Education: Role of Perceptions of School Climate and Self-Perception
Aibao Zhou, Xiangli Guan, Md Zahir Ahmed, Oli Ahmed, Mary C. Jobe, Fatema Akhter Hiramoni
Sustainability.2021; 13(10): 5475. CrossRef - Age moderates the associations between TRAbs, free T3 and outcomes of Graves’ disease patients with radioactive iodine treatment
Lusi Lu, Chenlu Gao, Nan Zhang
Clinical Endocrinology.2021; 94(2): 303. CrossRef - Vietnamese Students’ Satisfaction toward Higher Education Service: The Relationship between Education Service Quality and Educational Outcomes
Hong-Van Thi Dinh, Quynh Anh Thi Nguyen, Mai-Huong Thi Phan, Kien The Pham, Tham Nguyen, Hung Thanh Nguyen
European Journal of Educational Research.2021; volume-10-(volume-10-): 1397. CrossRef - Critical Determinants of Household Electricity Consumption in a Rapidly Growing City
Sharif Shofirun Sharif Ali, Muhammad Rizal Razman, Azahan Awang, M. R. M. Asyraf, M. R. Ishak, R. A. Ilyas, Roderick John Lawrence
Sustainability.2021; 13(8): 4441. CrossRef - Impacto prognóstico do défice de ferro nas síndromes coronárias agudas
Carina Silva, Juliana Martins, Isabel Campos, Carina Arantes, Carlos Galvão Braga, Nuno Salomé, António Gaspar, Pedro Azevedo, Miguel Álvares Pereira, Jorge Marques, Catarina Vieira
Revista Portuguesa de Cardiologia.2021; 40(8): 525. CrossRef - The Development and Psychometric Assessment of Malaysian Youth Adversity Quotient Instrument (MY-AQi) by Combining Rasch Model and Confirmatory Factor Analysis
Mohd Effendi Ewan Mohd Matore, Mohammed Afandi Zainal, Muhamad Firdaus Mohd Noh, Ahmad Zamri Khairani, Nordin Abd Razak
IEEE Access.2021; 9: 13314. CrossRef - ROMANTİK İLİŞKİSİ OLAN KADINLARDA ALGILANAN PARTNER DEĞİŞİMİ, YAKINLIK VE YAŞAM DOYUMU
Duygu DİNÇER
International Journal of Social Inquiry.2021; 14(2): 569. CrossRef - Modernising tactile acuity assessment; clinimetrics of semi-automated tests and effects of age, sex and anthropometry on performance
Nick A. Olthof, Michel W. Coppieters, G Lorimer Moseley, Michele Sterling, Dylan J. Chippindall, Daniel S. Harvie
PeerJ.2021; 9: e12192. CrossRef - Does the Brief Resilience Scale actually measure resilience and succumbing? Comparing artefactual and substantive models
Samuel McKay, Jason L. Skues, Ben J. Williams
Advances in Mental Health.2021; 19(2): 192. CrossRef - Factors associated with bone health status of Malaysian pre-adolescent children in the PREBONE-Kids Study
Chung Yuan Chang, Kanimolli Arasu, Soon Yee Wong, Shu Hwa Ong, Wai Yew Yang, Megan Hueh Zan Chong, Meenal Mavinkurve, Erwin Jiayuan Khoo, Karuthan Chinna, Connie Marie Weaver, Winnie Siew Swee Chee
BMC Pediatrics.2021;[Epub] CrossRef - COVID-19 Sürecinde Önleyici Davranışlar ile Yaşam Kalitesi Arasındaki İlişkinin İncelenmesi
Naif ERGÜN, Halis SAKIZ
Anemon Muş Alparslan Üniversitesi Sosyal Bilimler Dergisi.2021; 9(6): 1679. CrossRef - FACE-Q craniofacial module: Part 2 Psychometric properties of newly developed scales for children and young adults with facial conditions
Anne F Klassen, Charlene Rae, Wong Riff, Rafael Denadai, Dylan J Murray, Shirley Bracken, Douglas J Courtemanche, Neil Bulstrode, Justine O'Hara, Daniel Butler, Jesse Goldstein, Ali Tassi, Marinka LF Hol, David Johnson, Ingrid M. Ganske, Lars Kölby, Susan
Journal of Plastic, Reconstructive & Aesthetic Surgery.2021; 74(9): 2330. CrossRef - Öğrencilerin Türk Müziği Makamlarına ve Usullerine İlişkin Özyeterlik Algıları
Burcu Avcı Akbel
İnönü Üniversitesi Eğitim Fakültesi Dergisi.2021; 22(1): 68. CrossRef - Motivation and Intention Toward Physical Activity During the COVID-19 Pandemic: Perspectives From Integrated Model of Self-Determination and Planned Behavior Theories
Dojin Jang, Inwoo Kim, Sungho Kwon
Frontiers in Psychology.2021;[Epub] CrossRef - Assessing and solving multicollinearity in sediment transport prediction models using principal component analysis
Mohd Sofiyan Sulaiman, Manal Mohsen Abood, Shanker Kumar Sinnakaudan, Mohd Rizal Shukor, Goh Qiu You, Xiang Zhi Chung
ISH Journal of Hydraulic Engineering.2021; 27(sup1): 343. CrossRef - Predicting energy demand of residential buildings: A linear regression-based approach for a small sample size
Soufiane Boukarta
Selected Scientific Papers - Journal of Civil Engineering.2021; 16(2): 67. CrossRef - 3-7 Yaş Çocukların Depresif Belirtileri İle Annelerinin Kapsayıcı İşlevleri Arasındaki İlişki
Neslihan ZABCI, Elif EROL
AYNA Klinik Psikoloji Dergisi.2021; 8(3): 510. CrossRef - An analysis of note-taking strategies: The effect of translanguaging on content comprehension and knowledge retention
Xinyi Wang
Journal of Language Teaching.2021; 1(1): 18. CrossRef - The Role of Emotional Distress Tolerance on Fear Responding in a Heights-Fearful Sample: Perceived Versus Actual Behavior
Amber L. Billingsley, Shari A. Steinman
Behavior Therapy.2021; 52(4): 945. CrossRef - Development and preliminary psychometric investigation of the German Satisfaction with Comprehensive Cancer Care (SCCC) Questionnaire
Peter Esser, Leon Sautier, Susanne Sarkar, Georgia Schilling, Carsten Bokemeyer, Uwe Koch, Michael Friedrich, Gautier Defossez, Anja Mehnert-Theuerkauf
Health and Quality of Life Outcomes.2021;[Epub] CrossRef - Psychometric Properties of a Brief Metamemory and Metaconcentration Scale in Substance Use Problem
Md. Dilshad Manzar, Mohammed Salahuddin, Tufail Ahmad Khan, Showkat Ahmad Shah, Nymathullah Sharief Mohammad, Dejen Nureye, Habtamu Acho Addo, Wakuma Wakene Jifar, Abdulrhman Albougami
International Journal of Mental Health and Addiction.2021; 19(5): 1690. CrossRef - Autonomy support predicts language mindsets: Implications for developing communicative competence and willingness to communicate in EFL classrooms
Nourollah Zarrinabadi, Nigel Mantou Lou, Maryam Shirzad
Learning and Individual Differences.2021; 86: 101981. CrossRef - Teacher expectation effects in Chinese junior high schools: Exploring links between teacher expectations and student achievement using a hierarchical linear modelling approach
Shengnan Wang, Kane Meissel, Christine M. Rubie-Davies
Social Psychology of Education.2021; 24(5): 1305. CrossRef - Profiles of Expectations regarding Aging after Relocation to Assisted Living
Evan Plys, Ronald Smith
Journal of Aging and Environment.2021; 35(3): 319. CrossRef - Exploration of a Multi-Parameter Technology for Pain Assessment in Postoperative Patients After Cardiac Surgery in the Intensive Care Unit: The Nociception Level Index (NOL)TM
Céline Gélinas, Shiva Shahiri T, Melissa Richard-Lalonde, Denny Laporta, Jean-François Morin, Madalina Boitor, Catherine E Ferland, Patricia Bourgault, Philippe Richebé
Journal of Pain Research.2021; Volume 14: 3723. CrossRef - The psychometric properties of Social Anxiety Scale for Adolescents (SAS-A) short form-Bangla
Najifa Alam, Oli Ahmed, Lutfun Naher, Fatema Akhter Hiramoni
Heliyon.2021; 7(8): e07801. CrossRef - The Young and the Prejudiced? Millennial Men, “Dude Bro” Disposition, and LGBTQ Negativity in a US National Sample
Meredith G. F. Worthen
Sexuality Research and Social Policy.2021; 18(2): 290. CrossRef - The influence of team mindfulness on nurses' presenteeism: A cross‐sectional study from the perspective of sensemaking
Beini Liu, Haizhu Zhao, Yang Wang, Qiang Lu
Journal of Nursing Management.2021; 29(6): 1668. CrossRef - Early-life adversities and adult attachment in depression and alexithymia
Jani Kajanoja, Max Karukivi, Noora M. Scheinin, Hanna Ahrnberg, Linnea Karlsson, Hasse Karlsson
Development and Psychopathology.2021; 33(4): 1428. CrossRef - Reducing Objectification Could Tackle Stigma in the COVID-19 Pandemic: Evidence From China
Youli Chen, Jiahui Jin, Xiangyang Zhang, Qi Zhang, Weizhen Dong, Chun Chen
Frontiers in Psychology.2021;[Epub] CrossRef - ICD-11-Based Assessment of Social Media Use Disorder in Adolescents: Development and Validation of the Social Media Use Disorder Scale for Adolescents
Kerstin Paschke, Maria Isabella Austermann, Rainer Thomasius
Frontiers in Psychiatry.2021;[Epub] CrossRef - The impact of entrepreneurs’ prior experience and communication networks on perceived knowledge access
Wei Shi, Matthew Weber
Journal of Knowledge Management.2021; 25(5): 1406. CrossRef - Dyadic trust as a mediator in the association between posttraumatic stress symptoms and relationship distress in community couples
Eileen P. Barden, Binghuang A. Wang, Julia A. Sternberg, Leanna Z. Poole, Christina M. Balderrama-Durbin
Journal of Social and Personal Relationships.2021; 38(3): 950. CrossRef - Spanish Adaptation of the Overall Anxiety and Depression Severity and Impairment Scales in University Students
Jorge Osma, Víctor Martínez-Loredo, Amanda Díaz-García, Alba Quilez-Orden, Óscar Peris-Baquero
International Journal of Environmental Research and Public Health.2021; 19(1): 345. CrossRef - Tourists’ satisfaction with and intentions toward a nature-themed festival: The contribution of destination attributes, festival events, place attachment and life satisfaction
Bình Nghiêm-Phú, Thu Hương Kiều, Thị Thu Trang Hoàng
Journal of Convention & Event Tourism.2021; 22(3): 221. CrossRef - Elite athletes’ mental well-being and life satisfaction: a study of elite athletes’ resilience and social support from an Asian unrecognised National Olympic Committee
Angus C. H. Kuok, David K. I. Chio, Alan C. H. Pun
Health Psychology Report.2021;[Epub] CrossRef - Does Internal branding effect on Employee Performance? An Empirical Evidence from Services Sector of Pakistan.
Irfan Sabir, Agha Husna, Muhammad Bilal Majid, Mohd Sadad Mahmud, Naila Sabir
Journal of Public Value and Administrative Insight.2021; 4(1): 11. CrossRef - Shared-decision-making Behavior in Hospitalized Patients: Investigating the Impact of Patient's Trust in Physicians, Emotional Support, Informational Support, and Tendency to Excuse Using a Structural Equation Modeling Approach
Zahra Chegini, Sheikh Mohammed Shariful Islam
Journal of Patient Experience.2021;[Epub] CrossRef - Foreign language speaking competence and self‐regulated speaking motivation
Mehmet Sercan Uztosun
Foreign Language Annals.2021; 54(2): 410. CrossRef - Influence of culture on social representation of wines produced by various methods: Natural, organic and conventional
Isabel Urdapilleta, Samuel Demarchi, Wendy V. Parr
Food Quality and Preference.2021; 87: 104034. CrossRef - The relationship among factors of organizational justice, organizational citizenship behavior, job satisfaction, and ease of work among Japanese nurses.
Misako Shimamura, Mayumi Fukutake, Mineko Namba, Tetsuya Ogino
Applied Nursing Research.2021; 61: 151479. CrossRef - The role of passion and emotions in academic procrastination during a pandemic (COVID-19)
Sonia Rahimi, Robert J. Vallerand
Personality and Individual Differences.2021; 179: 110852. CrossRef - Foraging for New Ideas: Search and Research in Divergent Thinking Tasks
Ramón Martín-Brufau, Javier Corbalán Berná
Creativity Research Journal.2021; 33(3): 246. CrossRef - High‐involvement HRM and innovative behaviour: The mediating roles of nursing staff's autonomy and affective commitment
Maarten Renkema, Jan Leede, Llewellyn E. Van Zyl
Journal of Nursing Management.2021; 29(8): 2499. CrossRef - How does involvement affect attendees’ aboriginal tourism image? Evidence from aboriginal festivals in Taiwan
Tsung Hung Lee, Fen-Hauh Jan
Current Issues in Tourism.2021; 24(17): 2421. CrossRef - Characterizing change in students' self-assessments of understanding when engaged in instructional activities
Jenna Tashiro, Daniela Parga, John Pollard, Vicente Talanquer
Chemistry Education Research and Practice.2021; 22(3): 662. CrossRef - Impact of tourists’ psychological ownership of an eco-friendly trail on their behavior intention: an empirical investigation of Jeju Olle Trail in South Korea
Jihee Kim, Hyejo Hailey Shin, Miyoung Jeong, Won Seok Lee
Asia Pacific Journal of Tourism Research.2021; 26(10): 1097. CrossRef - Biochar restructures plant–soil–microbe relationships in a woody cropping system
Jake A. Nash, Jessica R. Miesel, Gregory M. Bonito, Monique L. Sakalidis, Han Ren, Daniel Warnock, Lisa K. Tiemann
Soil Science Society of America Journal.2021; 85(6): 2019. CrossRef - Predicting the physical activity of new parents who participated in a physical activity intervention
Ryan E. Rhodes, Mark R. Beauchamp, Alison Quinlan, Danielle Symons Downs, Darren E.R. Warburton, Chris M. Blanchard
Social Science & Medicine.2021; 284: 114221. CrossRef - Reply to: Misinterpretation of solid sphere equivalent refractive index measurements and smallest detectable diameters of extracellular vesicles by flow cytometry
George C. Brittain, Marc-André Langlois, Sergei Gulnik
Scientific Reports.2021;[Epub] CrossRef - Interplay between state anxiety, heart rate variability, and cognition: An ex-Gaussian analysis of response times
Derek P. Spangler, Katherine R. Cox, Julian F. Thayer, Justin R. Brooks, Bruce H. Friedman
International Journal of Psychophysiology.2021; 159: 60. CrossRef - The Strengths Use Scale: Psychometric Properties, Longitudinal Invariance and Criterion Validity
Llewellyn E. van Zyl, Diane Arijs, Matthew L. Cole, Aldona Gliíska-Newes, Lara C. Roll, Sebastiaan Rothmann, Rebecca Shankland, Jacqueline M. Stavros, Nicolas B. Verger
Frontiers in Psychology.2021;[Epub] CrossRef - Experience of Sexual Orientation Microaggression among Young Adult Lesbian, Gay, and Bisexual Individuals in Taiwan: Its Related Factors and Association with Mental Health Problems
Ching-Shu Tsai, Yu-Te Huang, Cheng-Fang Yen
International Journal of Environmental Research and Public Health.2021; 18(22): 11744. CrossRef - Higher Risk of Depression After Total Mastectomy Versus Breast Reconstruction Among Adult Women With Breast Cancer: A Systematic Review and Metaregression
Sriyani Padmalatha, Yi-Tseng Tsai, Han-Chang Ku, Yi-Lin Wu, Tsung Yu, Su-Ying Fang, Nai-Ying Ko
Clinical Breast Cancer.2021; 21(5): e526. CrossRef - Competitive Recovery–Stress and Mood States in Mexican Youth Athletes
Luis Felipe Reynoso-Sánchez, Germán Pérez-Verduzco, Miguel Ángel Celestino-Sánchez, Jeanette M. López-Walle, Jorge Zamarripa, Blanca Rocío Rangel-Colmenero, Hussein Muñoz-Helú, Germán Hernández-Cruz
Frontiers in Psychology.2021;[Epub] CrossRef - Developing and validating the Japanese version of professional attitude scale for nurses
N. Takada, K. Asakura, S. Sugiyama
International Nursing Review.2021; 68(1): 24. CrossRef - Covid-19 Pandemi Sürecinde Üniversite Öğrencilerinin İşlemsel Uzaklık Algısı İle Bilişötesi Farkındalığı Arasındaki İlişkinin İncelenmesi
Ahmet Berk USTUN
Bilgi ve İletişim Teknolojileri Dergisi.2021; 3(2): 175. CrossRef - Validation of the Death and Dying Distress Scale in patients with advanced cancer
Gilla K. Shapiro, Kenneth Mah, Madeline Li, Camilla Zimmermann, Sarah Hales, Gary Rodin
Psycho-Oncology.2021; 30(5): 716. CrossRef - A Validation Study of the Rainbow Model of Integrated Care-Measurement Tool for Patients in China
Xin Wang, Stephen Birch, Lijin Chen, Yixiang Huang, Pim Valentijn
International Journal of Integrated Care.2021;[Epub] CrossRef - How can socio-psychological factors be related to water-efficiency intention and behaviors among Iranian residential water consumers?
Seyyed Ahmadreza Shahangian, Massoud Tabesh, Masoud Yazdanpanah
Journal of Environmental Management.2021; 288: 112466. CrossRef - Traffic collision avoidance system: false injection viability
John Hannah, Robert Mills, Richard Dill, Douglas Hodson
The Journal of Supercomputing.2021; 77(11): 12666. CrossRef - Factors associated with coach–athlete conversations about mental health in intercollegiate sport
Jessica Murphy, Philip Sullivan
International Journal of Sports Science & Coaching.2021; 16(3): 509. CrossRef - Validation of Pictorial Mood Assessment with Ottawa Mood Scales and the Positive and Negative Affect Scale for Young Adults
Mei-Yi Wong, Paul E. Croarkin, Chen Kang Lee, Poh Foong Lee
Community Mental Health Journal.2021; 57(3): 529. CrossRef - Mediating effect of Maternal and Paternal Family Relationship between Neuroticism and Postpartum Depression: The Actor-Partner Interdependence Mediation Model
Hye Gyeong Seo, Suk-Sun Kim
Journal of Korean Academy of psychiatric and Mental Health Nursing.2021; 30(4): 400. CrossRef - The interacting roles and relative importance of climate, topography, soil properties and mineralogical composition on soil potassium variations at a national scale in China
Ting Li, Junjie Liang, Xiaoqin Chen, Huoyan Wang, Shirong Zhang, Yulin Pu, Xiaoxun Xu, Hao Li, Jingwen Xu, Xiaobo Wu, Xiaojing Liu
CATENA.2021; 196: 104875. CrossRef - Hungarian Version of the Family Relationship Questionnaire (FRQ)
Dora Csilla Kovács, Veronika Mészáros, Zsuzsanna Tanyi, Edit Jakubovits, Máté Smohai, Andrea Hübner, Wei Wang, Zsuzsanna Kövi
Interpersona: An International Journal on Personal Relationships.2021; 15(1): 36. CrossRef - Macro Patterns and Trends of U.S. Consumer Technological Innovation Diffusion Rates
Albert Joseph Parvin, Mario G. Beruvides
Systems.2021; 9(1): 16. CrossRef - Retrospective analysis of hemispheric structural network change as a function of location and size of glioma
Shawn D’Souza, Lisa Hirt, David R Ormond, John A Thompson
Brain Communications.2021;[Epub] CrossRef - Relationship between the fear of COVID-19 disease and sleep quality: the mediating role of stress
Rumana Ferdousi Siddique, Oli Ahmed, Kazi Nur Hossain
Heliyon.2021; 7(5): e07033. CrossRef - Proactive inhibition is not modified by deep brain stimulation for Parkinson's disease: An electrical neuroimaging study
Michael De Pretto, Michael Mouthon, Ines Debove, Claudio Pollo, Michael Schüpbach, Lucas Spierer, Ettore A. Accolla
Human Brain Mapping.2021; 42(12): 3934. CrossRef - Compulsive Internet Use Scale: Psychometric Properties and Associations With Sleeping Patterns, Mental Health, and Well-Being in Lithuanian Medical Students During the Coronavirus Disease 2019 Pandemic
Egle Milasauskiene, Julius Burkauskas, Aurelija Podlipskyte, Orsolya Király, Zsolt Demetrovics, Laurynas Ambrasas, Vesta Steibliene
Frontiers in Psychology.2021;[Epub] CrossRef - High School Students With Emotional and Behavioral Disorders Perceptions of School Climate
Nicholas A. Gage, Dennis A. Kramer, Kaci Ellis
Journal of Disability Policy Studies.2021; 32(2): 83. CrossRef - Kinematics of direct reaching in head-mounted and stereoscopic widescreen virtual environments
Chiuhsiang J. Lin, Betsha T. Abreham, Bereket H. Woldegiorgis
Virtual Reality.2021; 25(4): 1015. CrossRef - Trustworthiness in Higher Education: The Role of Professor Benevolence and Competence
Silvia Di Battista, Heather J. Smith, Chiara Berti, Monica Pivetti
Social Sciences.2021; 10(1): 18. CrossRef - Activity‐induced secretion of semaphorin 3A mediates learning
Aoi Jitsuki‐Takahashi, Susumu Jitsuki, Naoya Yamashita, Meiko Kawamura, Manabu Abe, Kenji Sakimura, Akane Sano, Fumio Nakamura, Yoshio Goshima, Takuya Takahashi
European Journal of Neuroscience.2021; 53(10): 3279. CrossRef - Conversion of PROMIS global health to EQ-5D health state values in patients undergoing lumbar spine surgery: A psychometric evaluation
Justin Turcotte, Maura Callanan, Brooke Buckley, Sohail Zaidi, Chad Patton
Journal of Orthopaedics.2021; 23: 67. CrossRef - The mediating role of problematic social media use in the relationship between social avoidance/distress and self-esteem
Oli Ahmed, Syeda Jannatun Nayeem Siddiqua, Najifa Alam, Mark D. Griffiths
Technology in Society.2021; 64: 101485. CrossRef - The Associations Between Computational Thinking and Creativity: The Role of Personal Characteristics
Rotem Israel-Fishelson, Arnon Hershkovitz, Andoni Eguíluz, Pablo Garaizar, Mariluz Guenaga
Journal of Educational Computing Research.2021; 58(8): 1415. CrossRef - Scaling the peak and steady-state aerobic power of running and walking humans
Heather M. Bowes, Catriona A. Burdon, Gregory E. Peoples, Sean R. Notley, Nigel A. S. Taylor
European Journal of Applied Physiology.2021; 121(10): 2925. CrossRef - The Utilization of National Tobacco Cessation Services among Female Smokers and the Need for a Gender-Responsive Approach
Ahnna Lee, Kang-Sook Lee, Dahyeon Lee, Hyeju Ahn, Hyun-Kyung Lee, Hyekyeong Kim, Jakyoung Lee, Hong-Gwan Seo
International Journal of Environmental Research and Public Health.2021; 18(10): 5313. CrossRef - The motivations of visiting upscale restaurants during the COVID-19 pandemic: The role of risk perception and trust in government
Bekir Bora Dedeoğlu, Erhan Boğan
International Journal of Hospitality Management.2021; 95: 102905. CrossRef - The Relationship between the Transformational Leadership, the Cultural Intelligence of Teachers and the Skills of Principals’ Diversity Management
Necati Cobanoglu
European Journal of Educational Management.2021; volume-4-2(volume-4-i): 35. CrossRef - Long-Wavelength–Filtered Light Transiently Inhibits Negative Lens-Induced Axial Eye Growth in the Chick Myopia Model
Nina Riddell, Sheila G. Crewther, Melanie J. Murphy, Yuki Tani
Translational Vision Science & Technology.2021; 10(9): 38. CrossRef - Adolescent Attachment to Parents and Peers and the Use of Instagram: The Mediation Role of Psychopathological Risk
Giulia Ballarotto, Barbara Volpi, Renata Tambelli
International Journal of Environmental Research and Public Health.2021; 18(8): 3965. CrossRef - Muscle strength and executive function in children and adolescents with autism spectrum disorder
Sebastian Ludyga, Uwe Pühse, Markus Gerber, Manuel Mücke
Autism Research.2021; 14(12): 2555. CrossRef - Development of the ‘SNS older adults measure’ (SNS-OA) to examine social network site use in older adults
Loveday Newman, Charlotte Stoner, Anne Corbett, Maria Megalogeni, Zunera Khan, Aimee Spector
Aging & Mental Health.2021; 25(1): 68. CrossRef - Adolescent gaming and social media usage before and during the COVID-19 pandemic
Kerstin Paschke, Maria Isabella Austermann, Kathrin Simon-Kutscher, Rainer Thomasius
SUCHT.2021; 67(1): 13. CrossRef - Spontaneous Self-Distancing Mediates the Association Between Working Memory Capacity and Emotion Regulation Success
T. H. Stanley Seah, Lindsey M. Matt, Karin G. Coifman
Clinical Psychological Science.2021; 9(1): 79. CrossRef - Comparing the Effect of Product-Based Metrics on the Translation Process
Bram Vanroy, Moritz Schaeffer, Lieve Macken
Frontiers in Psychology.2021;[Epub] CrossRef - The Mediating Role of Employee Innovativeness on the Nexus between Internet Banking and Employee Performance: Evidence from the Republic of Congo
Jean Baptiste Bernard Pea-Assounga, Hongxing Yao, Raffaele Carli
Mathematical Problems in Engineering.2021; 2021: 1. CrossRef - Using Contemporary Psychometric Methods to Construct and Validate Scores on a Short-Form Version of the Psychological Strain Scales
Jenny Mei Yiu Huen, Jie Zhang, Augustine Osman, Bob Lew, Paul Siu Fai Yip
Journal of Affective Disorders.2021; 281: 1. CrossRef - Socio‐economic status, executive functions, and theory of mind ability in adolescents: Relationships with language ability and cortisol
Graham Pluck, Marco A. Córdova, Christine Bock, Izan Chalen, Ana F. Trueba
British Journal of Developmental Psychology.2021; 39(1): 19. CrossRef - Enhancing Planning Behavior during Retirement: Effects of a Time Perspective Based Training Intervention
Anna Mooney, Cindy E. Tsotsoros, Joanne K. Earl, Douglas A. Hershey, Carl H. Mooney
Social Sciences.2021; 10(8): 306. CrossRef - Associated factors to the consumption of ultra-processed foods and its relation with dietary sources in Portugal
Vânia Magalhães, Milton Severo, Daniela Correia, Duarte Torres, Renata Costa de Miranda, Fernanda Rauber, Renata Levy, Sara Rodrigues, Carla Lopes
Journal of Nutritional Science.2021;[Epub] CrossRef - Preliminary investigation of interactive associations of sleep and pain with cognition in sedentary middle-aged and older adults
Ashley F. Curtis, Joseph M. Dzierzewski, Matthew P. Buman, Peter R. Giacobbi, Beverly L. Roberts, Adrienne T. Aiken-Morgan, Michael Marsiske, Christina S. McCrae
Journal of Clinical Sleep Medicine.2021; 17(2): 233. CrossRef - Confirming Profiles of Comorbid Psychological Symptoms in Urban Youth: Exploring Gender Differences and Trait Mindfulness
Lindsey Webb, Erica Sibinga, Rashelle Musci, Laura K. Clary, Tamar Mendelson
Journal of Youth and Adolescence.2021; 50(11): 2249. CrossRef - Patients’ health outcomes after an implementation intervention targeting the physiotherapists’ clinical behaviour
Johanna Fritz, Lena Almqvist, Anne Söderlund, Lars Wallin, Maria Sandborgh
Archives of Physiotherapy.2021;[Epub] CrossRef - Image-Based Machine Learning Algorithms for Disease Characterization in the Human Type 1 Diabetes Pancreas
Xiaohan Tang, Irina Kusmartseva, Shweta Kulkarni, Amanda Posgai, Stephan Speier, Desmond A. Schatz, Michael J. Haller, Martha Campbell-Thompson, Clive H. Wasserfall, Bart O. Roep, John S. Kaddis, Mark A. Atkinson
The American Journal of Pathology.2021; 191(3): 454. CrossRef - Network organisation and the dynamics of tubules in the endoplasmic reticulum
Hannah T. Perkins, Victoria J. Allan, Thomas A. Waigh
Scientific Reports.2021;[Epub] CrossRef - On Linear and Circular Approach to GPS Data Processing: Analyses of the Horizontal Positioning Deviations Based on the Adriatic Region IGS Observables
Davor Šakan, Serdjo Kos, Biserka Drascic Ban, David Brčić
Data.2021; 6(2): 9. CrossRef - Characteristics and neuropsychological impact of traumatic brain injury in female prisoners
Michelle O’Sullivan, Steven Fitzsimons, Sara da Silva Ramos, Michael Oddy, Annette Sterr
Brain Injury.2021; 35(1): 72. CrossRef - Community awareness towards coastal hazard and adaptation strategies in Pahang coast of Malaysia
Md. Mahfuzul Islam, A. Aldrie Amir, Rawshan Ara Begum
Natural Hazards.2021; 107(2): 1593. CrossRef - Investigation of Depression, Anxiety, and Stress and their Determinants of University Students during an Early Stage of COVID19 Pandemic, Zanjan, Iran 2020
Khadijeh Hajimiri, Zarintaj Hosseinzadeh-Shanjani, Mohammad Masoud Vakili, Fatemeh Jafari, Bahram Rostami
Journal of Human, Environment, and Health Promotion.2021; 7(3): 159. CrossRef - The influence of physiologic and atmospheric variables on spasticity after spinal cord injury
Anastasia Zarkou, Edelle C. Field-Fote
NeuroRehabilitation.2021; 48(3): 353. CrossRef - The Burnout Assessment Tool (BAT): A Contribution to Italian Validation with Teachers’
Giacomo Angelini, Ilaria Buonomo, Paula Benevene, Piermarco Consiglio, Luciano Romano, Caterina Fiorilli
Sustainability.2021; 13(16): 9065. CrossRef - The Feasibility of Using Instagram Data to Predict Exercise Identity and Physical Activity Levels: Cross-sectional Observational Study
Sam Liu, Megan Perdew, Alexander Lithopoulos, Ryan E Rhodes
Journal of Medical Internet Research.2021; 23(4): e20954. CrossRef - The impact of smart tourism technology and domestic travelers' technology readiness on their satisfaction and behavioral intention: A cross‐country comparison
Hyejo Hailey Shin, Miyoung Jeong, Mi‐Hea Cho
International Journal of Tourism Research.2021; 23(5): 726. CrossRef - An Adaptable, Open-Access Test Battery to Study the Fractionation of Executive-Functions in Diverse Populations
Gislaine A. V. Zanini, Monica C. Miranda, Hugo Cogo-Moreira, Ali Nouri, Alberto L. Fernández, Sabine Pompéia
Frontiers in Psychology.2021;[Epub] CrossRef - Reconstruction of the Denonvillier's fascia and posterior ligament of the external urethral sphincter: Assessment of its effect on urinary continence after laparoscopic radical prostatectomy
Pedro Sousa Passos, Sara Teixeira Anacleto, Rui Simeão Versos, Mário Cerqueira Alves, Paulo Oliveira Mota
Archivio Italiano di Urologia e Andrologia.2021; 93(3): 274. CrossRef - The pathways from perceived discrimination to self-rated health among the Chinese diaspora during the COVID-19 pandemic: investigation of the roles of depression, anxiety, and social support
Youli Chen, Zicong Wang, Weizhen Dong, Jia Huei Chen Xu, Sizhe Ji Wu, Xiangyang Zhang, Chun Chen
International Journal for Equity in Health.2021;[Epub] CrossRef - Cognitive Gain or Handicap: Magical Ideation and Self-Absorption in Clinical and Non-clinical Participants
János Kállai, Gábor Vincze, Imre András Török, Rita Hargitai, Sándor Rózsa, István Hartung, István Tamás, András Láng, Róbert Herold
Frontiers in Psychology.2021;[Epub] CrossRef - Tinder blue, mental flu? Exploring the associations between Tinder use and well-being
Yu-Chin Her, Elisabeth Timmermans
Information, Communication & Society.2021; 24(9): 1303. CrossRef - How to choose and interpret a statistical test? An update for budding researchers
Ahmad Najmi, Balakrishnan Sadasivam, Avik Ray
Journal of Family Medicine and Primary Care.2021; 10(8): 2763. CrossRef - Short-Term Effectiveness of the Youth Gambling Prevention Program “Who Really Wins?”—Results from the First National Implementation
Dora Dodig Hundric, Sabina Mandic, Neven Ricijas
International Journal of Environmental Research and Public Health.2021; 18(19): 10100. CrossRef - Factor Structure and Psychometric Properties of the Family Communication Scale in the Chinese Population
Ningyuan Guo, Henry C. Y. Ho, Man Ping Wang, Agnes Y. Lai, Tzu Tsun Luk, Kasisomayajula Viswanath, Sophia S. Chan, Tai Hing Lam
Frontiers in Psychology.2021;[Epub] CrossRef - Gender differences in predictors of technology threat avoidance
Andrew R. Gillam, Alina M. Waite
Information & Computer Security.2021; 29(3): 393. CrossRef - The effect of alcohol on mood among males drinking with a platonic friend
Molly A. Bowdring, Michael A. Sayette
Alcoholism: Clinical and Experimental Research.2021; 45(10): 2160. CrossRef - The scaling of human basal and resting metabolic rates
Heather M. Bowes, Catriona A. Burdon, Nigel A. S. Taylor
European Journal of Applied Physiology.2021; 121(1): 193. CrossRef - Personality Characteristics and Emotional Distress Among Chinese Pregnant Women: A Moderated Mediation Model
Wenjiao Yang, Yanfei Hou, Yu Chen, Wenting Liu, Fan Fang, Julan Xiao, Jing Wang
Frontiers in Psychiatry.2021;[Epub] CrossRef - Associations of the pre-pregnancy weight status with anaemia and the erythropoiesis-related micronutrient status
Noor Rohmah Mayasari, Tzu-Yu Hu, Jane C-J Chao, Chyi-Huey Bai, Yi Chun Chen, Ya Li Huang, Chun-Chao Chang, Fan-Fen Wang, Hamam Hadi, Esti Nurwanti, Jung-Su Chang
Public Health Nutrition.2021; 24(18): 6247. CrossRef - Re-examination of the Latent Structure of the Distress Intolerance Index
Keith P. Klein, Emily M. Bartholomay, Kimberly T. Stevens, Eva K. Harris, Thröstur Björgvinsson, Sarah J. Kertz
International Journal of Cognitive Therapy.2021; 14(2): 305. CrossRef - Positive emotional intensity and substance use: the underlying role of positive emotional avoidance in a community sample of military veterans
Melissa R. Schick, Nicole H. Weiss, Ateka C. Contractor, Emmanuel D. Thomas, Nichea S. Spillane
The American Journal of Drug and Alcohol Abuse.2021; 47(3): 373. CrossRef - Impact of bisphenol-A and synthetic estradiol on brain, behavior, gonads and sex hormones in a sexually labile coral reef fish
Jose A. Gonzalez, Abigail R. Histed, Ewelina Nowak, Dominica Lange, Sarah E. Craig, Coltan G. Parker, Achint Kaur, Supriya Bhuvanagiri, Kevin J. Kroll, Christopher J. Martyniuk, Nancy D. Denslow, Cheryl S. Rosenfeld, Justin S. Rhodes
Hormones and Behavior.2021; 136: 105043. CrossRef - Effect of leader-member exchange on construction worker safety behavior: Safety climate and psychological capital as the mediators
Changquan He, Brenda McCabe, Guangshe Jia
Safety Science.2021; 142: 105401. CrossRef - Entrepreneurial education exposure: a comparative investigation between technical and nontechnical higher education
Ayotunde Adetola Adelaja
Journal of Small Business and Enterprise Development.2021; 28(5): 711. CrossRef - Reading Struggle Stories of Role Models Can Improve Students' Growth Mindsets
Xu Du, Sheng Yuan, Ying Liu, Xuejun Bai
Frontiers in Psychology.2021;[Epub] CrossRef - Association between reported medication adherence and health-related quality of life in adult patients with haemophilia
Martina Bago, Ana Butkovic, Irena Preloznik Zupan, Barbara Faganel Kotnik, Ivana Prga, Vesna Bacic Vrca, Silva Zupancic Salek
International Journal of Clinical Pharmacy.2021; 43(6): 1500. CrossRef - Being Creative Makes You Happier: The Positive Effect of Creativity on Subjective Well-Being
Cher-Yi Tan, Chun-Qian Chuah, Shwu-Ting Lee, Chee-Seng Tan
International Journal of Environmental Research and Public Health.2021; 18(14): 7244. CrossRef - Predictors of Depressive Symptoms in Caregivers of Children with Attention-Deficit/Hyperactivity Disorder: A One-Year Follow-Up Study
Wen-Jiun Chou, Ray C. Hsiao, Chih-Cheng Chang, Cheng-Fang Yen
International Journal of Environmental Research and Public Health.2021; 18(16): 8835. CrossRef - European Portuguese Version of the User Satisfaction Evaluation Questionnaire (USEQ): Transcultural Adaptation and Validation Study
Célia Domingos, Patrício Soares Costa, Nadine Correia Santos, José Miguel Pêgo
JMIR mHealth and uHealth.2021; 9(6): e19245. CrossRef - Impact of CYP2A6 Activity on Nicotine Reinforcement and Cue-Reactivity in Daily Smokers
Kevin Butler, Meghan J Chenoweth, Ahmed El-Boraie, Haidy Giratallah, William J Kowalczyk, Stephen J Heishman, Rachel F Tyndale, Bernard Le Foll
Nicotine & Tobacco Research.2021; 23(10): 1735. CrossRef - Twelve Years of Postgraduate Palliative Medicine Training in Finland: How International Guidelines Are Implemented
Aija Vanhanen, Leila Niemi-Murola, Reino Pöyhiä
Palliative Medicine Reports.2021; 2(1): 242. CrossRef - Relationships between resilience, empathy, compassion fatigue, work engagement and turnover intention in haemodialysis nurses: A cross‐sectional study
Xiaoyi Cao, Lin Chen
Journal of Nursing Management.2021; 29(5): 1054. CrossRef - Investigation of the Turkish Cultural Adaptation of International Students Living in Turkey
Murat Gökalp, Khanım Eynullayeva, Bedri Yavuz Hatunoglu
The European Educational Researcher.2021; 4(2): 167. CrossRef - Psychometric Rigor of the Brief Religious Coping Measure (RCOPE) in Persian-Speaking Older Adults
Hassan Rezaeipandari, Mohammad Ali Morowatisharifabad, Asghar Mohammadpoorasl, Abdolreza Shaghaghi
Journal of Religion and Health.2021; 60(5): 3484. CrossRef - Learning or Leaving? Individual and Environmental Factors Related to Job Satisfaction and Turnover Intention
Ilmari J. A. Puhakka, Petri Nokelainen, Laura Pylväs
Vocations and Learning.2021; 14(3): 481. CrossRef - Do job insecurity, anxiety and depression caused by the COVID-19 pandemic influence hotel employees’ self-rated task performance? The moderating role of employee resilience
Teresa Aguiar-Quintana, Thi Hong Hai Nguyen, Yasmina Araujo-Cabrera, José M. Sanabria-Díaz
International Journal of Hospitality Management.2021; 94: 102868. CrossRef - Development and Psychometric Validation of the BREAST-Q Animation Deformity Scale for Women Undergoing an Implant-Based Breast Reconstruction After Mastectomy
Elena Tsangaris, Andrea L. Pusic, Manraj N. Kaur, Sophocles Voineskos, Louise Bordeleau, Toni Zhong, Raghavan Vidya, Justin Broyles, Anne F. Klassen
Annals of Surgical Oncology.2021; 28(9): 5183. CrossRef - Neurocognitive processes mediate the relation between children’s motor skills, cardiorespiratory fitness and response inhibition: Evidence from source imaging
Sebastian Ludyga, Wenke Möhring, Henning Budde, Nick Hirt, Uwe Pühse, Markus Gerber
Psychophysiology.2021;[Epub] CrossRef - The Gap Between Cognition and Adaptive Behavior in Students with Autism Spectrum Disorder: Implications for Social Anxiety and the Moderating Effect of Autism Traits
Gil Zukerman, Gili Yahav, Esther Ben-Itzchak
Journal of Autism and Developmental Disorders.2021; 51(5): 1466. CrossRef - The impact of technology usage on love and intimacy satisfaction among Portuguese adults
Mara Gomes, José Vasconcelos-Raposo, Carla M. Teixeira
Computers in Human Behavior Reports.2021; 4: 100084. CrossRef - Influence of Metacognition on Academic Achievement and Learning Style of Undergraduate Students in Tezpur University
Sradhanjali Pradhan, Parismita Das
European Journal of Educational Research.2021; volume-10-(volume-10-): 381. CrossRef - Mediating Role of Self-Disclosure in the Relationship between Attitudes towards Online Counselling and Perception of Social Stigma due to Receiving Psychological Help
Arzu Buyruk-Genc, Ece Kara
European Journal of Educational Research.2021; volume-10-(volume-10-): 919. CrossRef - Psychometric Evaluation of the Malay Version of the Multidimensional Beck Youth Inventories-2 (BYI-2 Malay): Measuring Self-Concept, Anxiety, Depression, Anger, and Disruptive Behaviour among Adolescents in Sheltered Homes
Wai-Eng Ding, Kit-Aun Tan, Jia-Yuin Fam, Firdaus Mukhtar, Munn-Sann Lye, Hamidin Awang, Khadeeja Munawar
Pertanika Journal of Social Sciences and Humanities.2021;[Epub] CrossRef - Social worldviews and social attitudes: Examining the psychological correlates for other-concern
Tosin Tunrayo Olonisakin, Sulaiman Olanrewaju Adebayo, Erhabor Sunday Idemudia
Journal of Culture and Values in Education.2021;[Epub] CrossRef - Psychological Distress Among HIV Healthcare Providers During the COVID-19 Pandemic in China: Mediating Roles of Institutional Support and Resilience
Cheuk Chi Tam, Shufang Sun, Xueying Yang, Xiaoming Li, Yuejiao Zhou, Zhiyong Shen
AIDS and Behavior.2021; 25(1): 9. CrossRef - Relationship between leader–member exchange and construction worker safety behavior: the mediating role of communication competence
Changquan He, Guangshe Jia, Brenda McCabe, Jide Sun
International Journal of Occupational Safety and Ergonomics.2021; 27(2): 371. CrossRef - Regression Modeling of the Effect of Chip Slenderness Ratio and Cutting Parameters on Vibration
Oktay ADIYAMAN
Gazi Üniversitesi Fen Bilimleri Dergisi Part C: Tasarım ve Teknoloji.2021; 9(4): 661. CrossRef - Self-Rated Aversion to Taste Qualities and the PROP Taster Phenotype Associate with Alcoholic Beverage Intake and Preference
Gary J. Pickering, Margaret K. Thibodeau
Beverages.2021; 7(2): 37. CrossRef - Introducing the Tactual Span: A New Task for Assessing Working Memory in the Teactile Modality
Eyal Heled, Shulamit Rotberg, Roman Yavich, A. Dan Hoofien
Assessment.2021; 28(3): 1018. CrossRef - Preventive strategy of flatfoot deformity using fully automated procedure
Che-Wei Hu, Peter Dabnichki, Arnold Baca, Canh Toan Nguyen, Toh Yen Pang
Medical Engineering & Physics.2021; 95: 15. CrossRef - The Consequences of Intrapreneurship in Exporting Firms: A Structural-model Approach
Gonçalo Bras, Miguel Torres Preto
SSRN Electronic Journal.2021;[Epub] CrossRef - Development and Psychometric Validation of a Patient-Reported Outcome Measure for Arm Lymphedema: The LYMPH-Q Upper Extremity Module
Anne F. Klassen, Elena Tsangaris, Manraj N. Kaur, Lotte Poulsen, Louise M. Beelen, Amalie Lind Jacobsen, Mads Gustaf Jørgensen, Jens Ahm Sørensen, Dalibor Vasilic, Joseph Dayan, Babak Mehrara, Andrea L. Pusic
Annals of Surgical Oncology.2021; 28(9): 5166. CrossRef - Differentiated Instruction between Application and Constraints: Teachers’ Perspective
Yousef Al-Shaboul, Manar Al-Azaizeh, Nasser Al-Dosari
European Journal of Educational Research.2021; volume-10-(volume-10-): 127. CrossRef - Validation of the Critical-Care Pain Observation Tool-Neuro in brain-injured adults in the intensive care unit: a prospective cohort study
Céline Gélinas, Mélanie Bérubé, Kathleen A. Puntillo, Madalina Boitor, Melissa Richard-Lalonde, Francis Bernard, Virginie Williams, Aaron M. Joffe, Craig Steiner, Rebekah Marsh, Louise Rose, Craig M. Dale, Darina M. Tsoller, Manon Choinière, David L. Stre
Critical Care.2021;[Epub] CrossRef - BAĞLANMA TÜRLERİ İLE YİYECEK NEOFOBİSİ (YENİLİKTEN KORKMA) VE YİYECEK NEOFİLİSİ (YENİLİK ARAMA) ARASINDAKİ İLİŞKİ
Burçin BOZ, Bayram ŞAHİN, Erdoğan KOÇ
Yönetim ve Ekonomi Araştırmaları Dergisi.2021; 19(4): 456. CrossRef - Mammography Image-Based Diagnosis of Breast Cancer Using Machine Learning: A Pilot Study
Maha M. Alshammari, Afnan Almuhanna, Jamal Alhiyafi
Sensors.2021; 22(1): 203. CrossRef - Self-rated familiarity with autism spectrum disorders among practicing nurses: a cross-sectional study in the palestinian nursing practice
Ramzi Shawahna
BMC Nursing.2021;[Epub] CrossRef - Associations between previous sport and exercise experience and physical literacy elements among physically inactive Danes
Peter Elsborg, Clara Heinze, Paulina S. Melby, Glen Nielsen, Peter Bentsen, Knud Ryom
BMC Public Health.2021;[Epub] CrossRef - Couple-Based Physical Activity Planning for New Parents: A Randomized Trial
Ryan E. Rhodes, Chris M. Blanchard, Alison Quinlan, Danielle Symons Downs, Darren E.R. Warburton, Mark R. Beauchamp
American Journal of Preventive Medicine.2021; 61(4): 518. CrossRef - ‘Feeling fat,’ eating pathology, and eating pathology-related impairment in young men and women
Adrienne Mehak, Sarah E. Racine
Eating Disorders.2021; 29(5): 523. CrossRef - Relationships between ICT competencies related to work, self-esteem, and self-regulated learning with engineering competencies
Buratin Khampirat, Yuriy Bilan
PLOS ONE.2021; 16(12): e0260659. CrossRef - Geostatistical Distribution of Net Radiation at Different Sky Conditions over West Africa
Olusola Samuel Ojo, Babatunde Adeyemi, Emmanuel Omonigho Ogolo
Earth Systems and Environment.2021; 5(1): 43. CrossRef - The Leiden Index of Depression Sensitivity-Revised (LEIDS-R) and its revision (LEIDS-RR): An investigation of the internal structure and conceptual validity in a Norwegian sample
Aslak E. Himle, Odd E. Havik, Jens C. Thimm
Nordic Psychology.2020; 72(4): 331. CrossRef - RETRACTED ARTICLE: Psychometric properties of a short version of the Job Anxiety Scale
Bjarne Schmalbach, Andreas Kalkbrenner, Markus Bassler, Andreas Hinz, Katja Petrowski
BMC Medical Research Methodology.2020;[Epub] CrossRef - Self‐medication Hypothesis and Family Socialization Theory: Examining Independent and Common Mechanisms Responsible for Binge Drinking
Kristy L. Soloski
Family Process.2020; 59(1): 288. CrossRef - Gender differences for theory-based determinants of muscle-strengthening physical activity in college-aged students: a moderation analysis
Grace Fairchild Saidi, Paul Branscum
Translational Behavioral Medicine.2020; 10(3): 781. CrossRef - Transfer of motor skill between virtual reality viewed using a head-mounted display and conventional screen environments
Julia M. Juliano, Sook-Lei Liew
Journal of NeuroEngineering and Rehabilitation.2020;[Epub] CrossRef - Factors Associated With Patient Satisfaction Measured Using a Guttman-Type Scale
Yvonne Versluijs, Laura E Brown, Mauna Rao, Amanda I Gonzalez, Matthew D Driscoll, David Ring
Journal of Patient Experience.2020; 7(6): 1211. CrossRef - Altıncı Sınıf Öğrencilerinin Bilişsel Stillerinin Cinsiyetlere ve Akademik Başarılarına Göre İncelenmesi
Zafer GÜNEY
Erzincan Üniversitesi Eğitim Fakültesi Dergisi.2020; 22(1): 276. CrossRef - Assessing ICD-11 Gaming Disorder in Adolescent Gamers: Development and Validation of the Gaming Disorder Scale for Adolescents (GADIS-A)
Kerstin Paschke, Maria Isabella Austermann, Rainer Thomasius
Journal of Clinical Medicine.2020; 9(4): 993. CrossRef - Exploring the Importance of Players’ Characteristics and Performance on Serve and Return of Serve in Winning the Women’s Singles Grand Slam Tennis Tournaments
A W Zainan Abidin, N A S Ruslan
Journal of Physics: Conference Series.2020; 1496(1): 012008. CrossRef - Differences in Distress and Utilization of Mental Health Services between 2005 and 2018: a Potential Trend?
Kristen Haeberlein, Luke Evans, Britanie Champaigne, Paul J. Handal
Psychiatric Quarterly.2020; 91(1): 11. CrossRef - Psychological mindedness as a mediator in the relationship between dysfunctional coping styles and depressive symptoms in caregivers of children with autism spectrum disorder
Nicholas Tze Ping Pang, Ruziana Masiran, Kit‐Aun Tan, Aminah Kassim
Perspectives in Psychiatric Care.2020; 56(3): 649. CrossRef - Selected psychometric aspects of the Polish version of the Liverpool Self-efficacy Scale
Joanna Dymecka, Rafał Gerymski, Mariola Bidzan
Current Issues in Personality Psychology.2020; 8(4): 339. CrossRef - Is the Arrhenius-correction of biodegradation rates, as recommended through REACH guidance, fit for environmentally relevant conditions? An example from petroleum biodegradation in environmental systems
David M. Brown, Louise Camenzuli, Aaron D. Redman, Chris Hughes, Neil Wang, Eleni Vaiopoulou, David Saunders, Alex Villalobos, Susannah Linington
Science of The Total Environment.2020; 732: 139293. CrossRef - Illness Perceptions, Coping Strategies, and Quality of Life in People With Multiple Chronic Conditions
Cheng Cheng, Cong‐Yan Yang, Kerry Inder, Sally Wai-Chi Chan
Journal of Nursing Scholarship.2020; 52(2): 145. CrossRef - Assessment of Person-Centered Care in Gerontology Services: A new tool for healthcare professionals
Teresa Martínez, Victor Martínez-Loredo, Marcelino Cuesta, José Muñiz
International Journal of Clinical and Health Psychology.2020; 20(1): 62. CrossRef - Electronic government adoption in voluntary environments – a case study of Zimbabwe
Willard Munyoka
Information Development.2020; 36(3): 414. CrossRef - Confirmation of a measurement model for manufacturing flexibility development practices
Ruchi Mishra
International Journal of Quality & Reliability Management.2020; 38(1): 317. CrossRef - Relationships between Trait Emotional Intelligence, mood states, and future orientation among female Italian victims of Intimate Partner Violence
Cristina Cabras, Marina Mondo, Angelica Diana, Cristina Sechi
Heliyon.2020; 6(11): e05538. CrossRef - A Comprehensive Model to Explain Europeans’ Environmental Behaviors
Öykü Hazal Aral, Jordi López-Sintas
Sustainability.2020; 12(10): 4307. CrossRef - Tunable Q wavelet transform based emotion classification in Parkinson’s disease using Electroencephalography
Murugappan Murugappan, Waleed Alshuaib, Ali K. Bourisly, Smith K. Khare, Sai Sruthi, Varun Bajaj, Subash C. B. Gopinath
PLOS ONE.2020; 15(11): e0242014. CrossRef - Autonomic cardiovascular adaptations to acute head-out water immersion, head-down tilt and supine position
Florian Chouchou, Vincent Pichot, Frédéric Costes, Mailys Guillot, Jean-Claude Barthélémy, Laurent Bertoletti, Frédéric Roche
European Journal of Applied Physiology.2020; 120(2): 337. CrossRef - The Role of Motor Competences in Predicting Working Memory Maintenance and Preparatory Processing
Sebastian Ludyga, Manuel Mücke, Keita Kamijo, Christian Andrä, Uwe Pühse, Markus Gerber, Christian Herrmann
Child Development.2020; 91(3): 799. CrossRef - Psychometric Properties of the Chinese Version of Short-Form Community Attitudes Toward Mentally Illness Scale in Medical Students and Primary Healthcare Workers
Yan Tong, Zhizhong Wang, Yan Sun, Shulan Li
Frontiers in Psychiatry.2020;[Epub] CrossRef - Personal resilience factors protect against distressing auditory hallucinations: A study comparing psychotic patients with auditory hallucinations, non-patients with auditory hallucinations, and healthy controls
Julien Laloyaux, Alberto Collazzoni, Marco Hirnstein, Isabella Kusztrits, Frank Larøi
Psychiatry Research.2020; 290: 113058. CrossRef - Do higher-class individuals feel more entitled? The role of system-justifying belief
Bu-Xiao Xu, Shen-Long Yang, Jing Li, Ye Li, Yong-Yu Guo
The Journal of Social Psychology.2020; 160(4): 445. CrossRef - Distinct Routes to Understand the Relationship Between Dispositional Optimism and Life Satisfaction: Self-Control and Grit, Positive Affect, Gratitude, and Meaning in Life
Xavier Oriol, Rafael Miranda, César Bazán, Estefany Benavente
Frontiers in Psychology.2020;[Epub] CrossRef - The Concerns, Difficulties, and Stressors of Caring for Pets during COVID-19: Results from a Large Survey of U.S. Pet Owners
Jennifer W. Applebaum, Camie A. Tomlinson, Angela Matijczak, Shelby E. McDonald, Barbara A. Zsembik
Animals.2020; 10(10): 1882. CrossRef - Differential associations of neurobehavioral traits and cognitive ability to academic achievement in higher education
Graham Pluck, Patricia Bravo Mancero, Paola Alexandra Ortíz Encalada, Angélica María Urquizo Alcívar, Claudio E. Maldonado Gavilanez, Paola Chacon
Trends in Neuroscience and Education.2020; 18: 100124. CrossRef - Accelerometer based assessment of daily physical activity and sedentary time in adolescents with idiopathic scoliosis
Swati Chopra, A. Noelle Larson, Kenton R. Kaufman, Todd A. Milbrandt, Patrick Bergman
PLOS ONE.2020; 15(9): e0238181. CrossRef - Morale in Old Age and Its Association with Sociodemographic, Social, and Health-Related Factors in Different Age Groups
Marina Näsman, Johan Niklasson, Jan Saarela, Mikael Nygård, Birgitta Olofsson, Yngve Gustafson, Fredrica Nyqvist
Journal of Aging Research.2020; 2020: 1. CrossRef - Application of standardised effect sizes to hospital discharge outcomes for people with diabetes
Tim Robbins, Sarah N. Lim Choi Keung, Sailesh Sankar, Harpal Randeva, Theodoros N. Arvanitis
BMC Medical Informatics and Decision Making.2020;[Epub] CrossRef - Homogeneity of thermal tasters and implications for mechanisms and classification
Margaret Thibodeau, Martha Bajec, Anthony Saliba, Gary Pickering
Physiology & Behavior.2020; 227: 113160. CrossRef - Development and Validation of a Measure of Responsive Sexual Desire
Julia Velten, Samantha J. Dawson, Kelly Suschinsky, Lori A. Brotto, Meredith L. Chivers
Journal of Sex & Marital Therapy.2020; 46(2): 122. CrossRef - Finding the missing Einsteins: Expanding the breadth of cognitive and noncognitive measures used in academic services
Jonathan Wai, Joni M. Lakin
Contemporary Educational Psychology.2020; 63: 101920. CrossRef - Letter to the Editor regarding article, “Shenfu injection for improving cellular immunity and clinical outcome in patients with sepsis or septic shock”
Shuai Zhao, Shuling Liu, Qiuping Huang, Zhishang Li, Jing Zeng, Hairong Cai, Xingui Cai, Sicong Luo, Weizhang Zhang, Bojun Chen
The American Journal of Emergency Medicine.2020; 38(4): 841. CrossRef - Translation, Validation, and Psychometric Properties of Breastfeeding Self-Efficacy Scale—Short Form Among Iranian Women
Azadeh Asgarian, Maryam Hashemi, Mansoureh Pournikoo, Tayebe-Sadat Mirazimi, Hadi Zamanian, Mohammadali Amini-Tehrani
Journal of Human Lactation.2020; 36(2): 227. CrossRef - The Effect of an 8 Week Prescribed Exercise and Low-Carbohydrate Diet on Cardiorespiratory Fitness, Body Composition and Cardiometabolic Risk Factors in Obese Individuals: A Randomised Controlled Trial
Maria Perissiou, Erika Borkoles, Kent Kobayashi, Remco Polman
Nutrients.2020; 12(2): 482. CrossRef - Predicting milk mid-infrared spectra from first-parity Holstein cows using a test-day mixed model with the perspective of herd management
P. Delhez, F. Colinet, S. Vanderick, C. Bertozzi, N. Gengler, H. Soyeurt
Journal of Dairy Science.2020; 103(7): 6258. CrossRef - Infants’ gaze exhibits a fractal structure that varies by age and stimulus salience
Isabella C. Stallworthy, Robin Sifre, Daniel Berry, Carolyn Lasch, Tim J. Smith, Jed T. Elison
Scientific Reports.2020;[Epub] CrossRef - Premovement Suppression of Corticospinal Excitability may be a Necessary Part of Movement Preparation
J Ibáñez, R Hannah, L Rocchi, J C Rothwell
Cerebral Cortex.2020; 30(5): 2910. CrossRef - Theory of Mind, Self-Knowledge, and Perceptions of Loneliness in Emerging Adolescents
Sandra Bosacki, Flavia Pissoto Moreira, Valentina Sitnik, Katherine Andrews, Victoria Talwar
The Journal of Genetic Psychology.2020; 181(1): 14. CrossRef - Parenting Style and Emotional Distress Among Chinese College Students: A Potential Mediating Role of the Zhongyong Thinking Style
Yanfei Hou, Rong Xiao, Xueling Yang, Yu Chen, Fei Peng, Shegang Zhou, Xihua Zeng, Xiaoyuan Zhang
Frontiers in Psychology.2020;[Epub] CrossRef - Plasticity induced by pairing brain stimulation with motor-related states only targets a subset of cortical neurones
Jaime Ibáñez, L. Fu, L. Rocchi, M. Spanoudakis, D. Spampinato, D. Farina, John C. Rothwell
Brain Stimulation.2020; 13(2): 464. CrossRef - Perfectionism and foreign language achievement: The mediating role of emotions and achievement goals
Elyas Barabadi, Gholam Hassan Khajavy
Studies in Educational Evaluation.2020; 65: 100874. CrossRef - Facing obesity in pain rehabilitation clinics: Profiles of physical activity in patients with chronic pain and obesity—A study from the Swedish Quality Registry for Pain Rehabilitation (SQRP)
Huan-Ji Dong, Britt Larsson, Marcelo Rivano Fischer, Björn Gerdle, Adewale L. Oyeyemi
PLOS ONE.2020; 15(9): e0239818. CrossRef - Impact of the caregiver burden on the effectiveness of a home-based palliative care program: A mediation analysis
Angela J. Pereira-Morales, Luis Enrique Valencia, Luis Rojas
Palliative and Supportive Care.2020; 18(3): 332. CrossRef - Social-Ecological measure of resilience: an adapted measure forPersian-speaking university students
Mohammadali Amini-Tehrani, Mohammad Nasiri, Raheleh Sadeghi, Elahe-Sadat Hoseini, Tina Jalali, Hadi Zamanian
Health Promotion Perspectives.2020; 10(3): 207. CrossRef - Correlates of Perceived Physical Activity Transitions during the COVID‐19 Pandemic among Canadian Adults
Ryan E. Rhodes, Sam Liu, Alexander Lithopoulos, Chun‐Qing Zhang, Mauricio A. Garcia‐Barrera
Applied Psychology: Health and Well-Being.2020; 12(4): 1157. CrossRef - Psychological Factors that Lessen the Impact of COVID-19 on the Self-Employment Intention of Business Administration and Economics’ Students from Latin America
Brizeida Raquel Hernández-Sánchez, Giuseppina Maria Cardella, José Carlos Sánchez-García
International Journal of Environmental Research and Public Health.2020; 17(15): 5293. CrossRef - Developmental fitness curves: assessing sprint acceleration relative to age and maturity status in elite junior tennis players
Gillian K. Myburgh, Sean P. Cumming, Manuel Coelho-e-Silva, Robert M. Malina
Annals of Human Biology.2020; 47(4): 336. CrossRef - Team Emotional Intelligence in Working Contexts: Development and Validation of the Team-Trait Meta Mood Scale (T-TMMS)
Aitor Aritzeta, Rosa Mindeguia, Goretti Soroa, Nekane Balluerka, Arantxa Gorostiaga, Unai Elorza, Jone Aliri
Frontiers in Psychology.2020;[Epub] CrossRef - Exploring Cognitive Frailty: Prevalence and Associations with Other Frailty Domains in Older People with Different Degrees of Cognitive Impairment
Ellen E. De Roeck, Anne van der Vorst, Sebastiaan Engelborghs, G.A. Rixt Zijlstra, Eva Dierckx
Gerontology.2020; 66(1): 55. CrossRef - Development and Validation of the Krio Version of the WHOQOL-BREF for Use in Sierra Leone
Brian K. Price, John A. Conteh, Rebecca Esliker
SN Comprehensive Clinical Medicine.2020; 2(1): 42. CrossRef - Caffeine Use and Associations With Sleep in Adolescents With and Without ADHD
Caroline N Cusick, Joshua M Langberg, Rosanna Breaux, Cathrin D Green, Stephen P Becker
Journal of Pediatric Psychology.2020; 45(6): 643. CrossRef - Applicability of the social identity model of collective action in predicting support for interreligious violence in Indonesia
Tery Setiawan, Peer Scheepers, Carl Sterkens
Asian Journal of Social Psychology.2020; 23(3): 278. CrossRef - Intrinsic functional brain connectivity patterns underlying enhanced interoceptive sensibility
Xiaoqin Wang, Yafei Tan, Omer Van den Bergh, Andreas von Leupoldt, Jiang Qiu
Journal of Affective Disorders.2020; 276: 804. CrossRef - Driver Stress State Evaluation by Means of Thermal Imaging: A Supervised Machine Learning Approach Based on ECG Signal
Daniela Cardone, David Perpetuini, Chiara Filippini, Edoardo Spadolini, Lorenza Mancini, Antonio Maria Chiarelli, Arcangelo Merla
Applied Sciences.2020; 10(16): 5673. CrossRef - Identifying Different Ways People Change: A Latent Basis Growth Mixture Model Example Identifying Nonlinear Trajectories of Binge Drinking
Kristy L. Soloski, Jared A. Durtschi
Journal of Marital and Family Therapy.2020; 46(4): 638. CrossRef - İÇSEL PAZARLAMA UYGULAMALARININ ÖRGÜTSEL BAĞLILIĞA ETKİSİ: BANKACILIK SEKTÖRÜNDE BİR UYGULAMA
Ahmet SONGUR, Nazlı KARATAŞ
Bolu Abant İzzet Baysal Üniversitesi Sosyal Bilimler Enstitüsü Dergisi.2020; 20(2): 439. CrossRef - Concurrent strength and sprint training increases resting metabolic rate in masters road cyclists
Luke Delvecchio, Peter Reaburn, Jarrod Meerkin, Marko T. Korhonen, Nattai Borges, Campbell Macgregor, Mike Climstein
Movement & Sport Sciences - Science & Motricité.2020; (109): 39. CrossRef - Milli Takım Sporcularının Antrenör Davranışlarına İlişkin Görüşlerinin Bazı Değişkenlere Göre İncelenmesi
Orhan GÖK, İlyas OKAN
Gaziantep Üniversitesi Spor Bilimleri Dergisi.2020; 5(4): 486. CrossRef - Existe uma relação entre autocompaixão e adição à comida em mulheres com comportamentos alimentares disfuncionais?
Jônatas Oliveira, Samira Oskinis, Angélica Carreira dos Santos, Táki Athanássios Cordás
Jornal Brasileiro de Psiquiatria.2020; 69(4): 211. CrossRef - Can the use of government Apps shape citizen compliance? The mediating role of different perceptions of government
Ge Wang, Qiang Chen, Zengyang Xu, Xiangming Leng
Computers in Human Behavior.2020; 108: 106335. CrossRef - Atherosclerosis impacts the link between hepatocyte growth factor and cognition
Nermien N. Adly, Wessam H. El-kawaly, Hoda A. Abdelsattar
Journal of Gerontology and Geriatrics.2020; 68(1): 17. CrossRef - Multiple mediation effects of health locus of control and hope on the relationship between stroke patients’ social support and self-management
Ting-Ting Lei, Hong-Mei Han, Xiao-Jing Liu
Frontiers of Nursing.2020; 7(1): 49. CrossRef - The effect of supervisory neglect on adolescent peer victimization: Mediating role of self-esteem and internalizing problems
Seunghee Baeg, Boram Lee, Hye Jun Park
Children and Youth Services Review.2020; 111: 104839. CrossRef - Unlocking the customer engagement-brand loyalty relationship in tourism social media: The roles of brand attachment and customer trust
Ming-Way Li, Hsiu-Yu Teng, Chien-Yu Chen
Journal of Hospitality and Tourism Management.2020; 44: 184. CrossRef - Motivational Mindsets and Reasons for Studying: Development and Validation of a Classification Tool
Job Hudig, Ad W. A. Scheepers, Michaela Schippers, Guus Smeets
SSRN Electronic Journal .2020;[Epub] CrossRef - Comparison of resilience and quality of life between adolescent blood cancer survivors and those with congenital heart disease: a cross sectional study.
Sunhee Lee, Nack-Gyun Chung, Jae Young Choi
Health and Quality of Life Outcomes.2020;[Epub] CrossRef - How personality affects environmentally responsible behaviour through attitudes towards activities and environmental concern: evidence from a national park in Taiwan
Yung-Sen Chen, Yi Hsien Lin, Yueh-Jung Wu
Leisure Studies.2020; 39(6): 825. CrossRef - Guests’ perceptions of robot concierge and their adoption intentions
Hyejo Hailey Shin, Miyoung Jeong
International Journal of Contemporary Hospitality Management.2020; 32(8): 2613. CrossRef - Windkessel Model-Based Cuffless Blood Pressure Estimation Using Continuous Wave Doppler Ultrasound System
Biswabandhu Jana, Kamal Oswal, Sankar Mitra, Goutam Saha, Swapna Banerjee
IEEE Sensors Journal.2020; 20(17): 9989. CrossRef - Relationship between role stressors, job tasks and job satisfaction among health surveillance assistants in Malawi: a cross-sectional study
Simon Ntopi, Ellen Chirwa, Alfred Maluwa
BMJ Open.2020; 10(11): e037000. CrossRef - Structure and Psychometric Properties of the Penn State Worry Questionnaire for Children in Chinese Adolescents
Yixing Liu, Jie Zhong
Journal of Abnormal Child Psychology.2020; 48(11): 1499. CrossRef - The effect of digital reminiscence therapy on people with dementia: a pilot randomized controlled trial
SeolHwa Moon, Kyongok Park
BMC Geriatrics.2020;[Epub] CrossRef - Enhanced Permutation Tests via Multiple Pruning
Sangseob Leem, Iksoo Huh, Taesung Park
Frontiers in Genetics.2020;[Epub] CrossRef - A Web-Based Adaptation of the Quality of Life in Bipolar Disorder Questionnaire: Psychometric Evaluation Study
Emma Morton, Sharon HJ Hou, Oonagh Fogarty, Greg Murray, Steven Barnes, Colin Depp, Erin Michalak
JMIR Mental Health.2020; 7(4): e17497. CrossRef - The summer learning effect in writing in New Zealand
Frauke Meyer, Esther S. Yao, Kane Meissel
Reading and Writing.2020; 33(5): 1183. CrossRef - Relationship among independence of daily living, human relationships, and preparation for bereavement among healthy elderly Japanese people
Mayumi Fukutake, Misako Shimamura, Mineko Namba, Tetsuya Ogino
Psychogeriatrics.2020; 20(4): 437. CrossRef - EUPRON: nurses’ practice in interprofessional pharmaceutical care in Europe. A cross-sectional survey in 17 countries
Elyne De Baetselier, Bart Van Rompaey, Luis M Batalha, Monica Bergqvist, Bozena Czarkowska-Paczek, Alberto De Santis, Nienke E Dijkstra, Maria I Fernandes, Izabela Filov, Vigdis Abrahamsen Grøndahl, Jana Heczkova, Ann Karin Helgesen, Michael Isfort, Susan
BMJ Open.2020; 10(6): e036269. CrossRef - Creating and Validating a Shortened Version of the Community Balance and Mobility Scale for Application in People Who Are 61 to 70 Years of Age
Katharina Gordt, A Stefanie Mikolaizak, Kristin Taraldsen, Ronny Bergquist, Jeanine M Van Ancum, Corinna Nerz, Mirjam Pijnappels, Andrea B Maier, Jorunn L Helbostad, Beatrix Vereijken, Clemens Becker, Michael Schwenk
Physical Therapy.2020; 100(1): 180. CrossRef - Associations between symptoms of problematic smartphone, Facebook, WhatsApp, and Instagram use: An item-level exploratory graph analysis perspective
Dmitri Rozgonjuk, Cornelia Sindermann, Jon D. Elhai, Alexander P. Christensen, Christian Montag
Journal of Behavioral Addictions.2020; 9(3): 686. CrossRef - Relationship between multidimensional perfectionism and cognitive flexibility in university students
Zeynep Akkuş çutuk
Journal of Human Sciences.2020; 17(4): PDF. CrossRef - A Rainbow Wave? LGBTQ Liberal Political Perspectives During Trump’s Presidency: an Exploration of Sexual, Gender, and Queer Identity Gaps
Meredith G. F. Worthen
Sexuality Research and Social Policy.2020; 17(2): 263. CrossRef - Do Fellows and Faculty Share the Same Perception of Simulation Fidelity? A Pilot Study
Devika Singh, Taiki Kojima, Harshad Gurnaney, Ellen S. Deutsch
Simulation in Healthcare: The Journal of the Society for Simulation in Healthcare.2020; 15(4): 266. CrossRef - The Intergenerational Transmission of Self-Esteem in Young Elementary School Children: Focusing on Family Interactions
Suhyun Lee, Hyeeun Chung
Korean Journal of Child Studies.2020; 41(5): 73. CrossRef - Do Derivatives Hinder the Financial Contagion? A Case Study of Developed Countries’ Stock Markets
Saeed Rasekhi, Nasim Nabavi
Journal of Business Strategy Finance and Management.2020; 2(1-2): 89. CrossRef - Affect variability and emotional reactivity in generalized anxiety disorder
Rachel M. Ranney, Evelyn Behar, Alissa S. Yamasaki
Journal of Behavior Therapy and Experimental Psychiatry.2020; 68: 101542. CrossRef - Fear of Missing Out (FoMO) and social media’s impact on daily-life and productivity at work: Do WhatsApp, Facebook, Instagram, and Snapchat Use Disorders mediate that association?
Dmitri Rozgonjuk, Cornelia Sindermann, Jon D. Elhai, Christian Montag
Addictive Behaviors.2020; 110: 106487. CrossRef - Automatic Imitation in Comorbid PTSD & Alcohol Use Disorder and Controls: an RCT of Intranasal Oxytocin
Tyler E. Morrison, Lize De Coster, Christopher S. Stauffer, Jin Wen, Elnaz Ahmadi, Kevin Delucchi, Aoife O’Donovan, Josh Woolley
Psychoneuroendocrinology.2020; 120: 104787. CrossRef - Oxygen isotope homogeneity assessment for apatite U‐Th‐Pb geochronology reference materials
Qing Yang, Xiao‐Ping Xia, Le Zhang, Wanfeng Zhang, Yanqiang Zhang, Linli Chen, Yanan Yang, Miaohong He
Surface and Interface Analysis.2020; 52(5): 197. CrossRef - Data transformation: a focus on the interpretation
Dong Kyu Lee
Korean Journal of Anesthesiology.2020; 73(6): 503. CrossRef - Destination brand identity and emerging market tourists’ perceptions
Chang-Hua Yen, Hsiu-Yu Teng, Sue-Ting Chang
Asia Pacific Journal of Tourism Research.2020; 25(12): 1311. CrossRef - Urinary Volatile Terpenes Analyzed by Gas Chromatography–Mass Spectrometry to Monitor Breast Cancer Treatment Efficacy in Mice
Mark Woollam, Meghana Teli, Shengzhi Liu, Ali Daneshkhah, Amanda P. Siegel, Hiroki Yokota, Mangilal Agarwal
Journal of Proteome Research.2020; 19(5): 1913. CrossRef - A Brief Assessment of Body Image Perception: Norm Values and Factorial Structure of the Short Version of the FKB-20
Ileana Schmalbach, Bjarne Schmalbach, Markus Zenger, Hendrik Berth, Cornelia Albani, Katja Petrowski, Elmar Brähler
Frontiers in Psychology.2020;[Epub] CrossRef - Measuring the effectiveness of PBL through shape parameters and classification
Shilpa Bhaskar Mujumdar, Haridas Acharya, Shailaja Shirwaikar
Journal of Applied Research in Higher Education.2020; 13(1): 342. CrossRef - Predictors of Perceived Learning in a Distance Learning Environment from the Perspective of SIPS Model
Derya Orhan Göksün
International Journal of Human–Computer Interaction.2020; 36(10): 941. CrossRef - Emotion Differentiation as a Protective Factor Against the Behavioral Consequences of Rumination: A Conceptual Replication and Extension in the Context of Social Anxiety
T. H. Stanley Seah, Pallavi Aurora, Karin G. Coifman
Behavior Therapy.2020; 51(1): 135. CrossRef - Developing a “benefits of parental feeding behaviors” questionnaire for parents of preschoolers in urban Thailand
Chollada Jongsomjitt, Waraporn Chaiyawat, Branom Rodcumdee
Journal of Health Research.2020; 35(1): 15. CrossRef - Psychosocial intervention utilization and substance abuse treatment outcomes in a multisite sample of individuals who use opioids
Laura M. Harvey, Weihua Fan, Miguel Ángel Cano, Ellen L. Vaughan, Consuelo Arbona, Saman Essa, Helen Sanchez, Marcel A. de Dios
Journal of Substance Abuse Treatment.2020; 112: 68. CrossRef - Factors affecting risky cybersecurity behaviors by U.S. workers: An exploratory study
Andrew R. Gillam, W. Tad Foster
Computers in Human Behavior.2020; 108: 106319. CrossRef - MindMasters 2: A 3-Month Pilot Study Evaluating Grade 3 Children’s Social and Emotional Skills
Alexandre Santos, Corrine Langill
Canadian Journal of School Psychology.2020; 35(2): 123. CrossRef - Relationship between Parental Burnout Level and Perceived Social Support Levels of Parents of Children with Autism Spectrum Disorder
Avsar Ardic
International Journal of Educational Methodology.2020; 6(3): 533. CrossRef - Motivational Mindsets and Reasons for Studying: Development and Validation of a Classification Tool
Job Hudig, Ad W. A. Scheepers, Michaéla C. Schippers, Guus Smeets
Frontiers in Psychology.2020;[Epub] CrossRef - Adolescents and Body Uneasiness: the Contribution of Supportive Parenting and Trait Emotional Intelligence
Maria C. Gugliandolo, Sebastiano Costa, Francesca Cuzzocrea, Rosalba Larcan, Gabriella Martino
Journal of Child and Family Studies.2020; 29(9): 2453. CrossRef - Predicting Construction Labor Productivity Based on Implementation Levels of Human Resource Management Practices
Argaw Tarekegn Gurmu, Citra S. Ongkowijoyo
Journal of Construction Engineering and Management.2020;[Epub] CrossRef - Attempts to Limit Censoring in Measures of Patient Satisfaction
Cindy Nguyen, Joost T P Kortlever, Amanda I Gonzalez, David Ring, Laura E Brown, Jason R Somogyi
Journal of Patient Experience.2020; 7(6): 1094. CrossRef - Effect of a Diet Supplemented with the Moringa oleifera Seed Powder on the Performance, Egg Quality, and Gene Expression in Japanese Laying Quail under Heat-Stress
Reham Abou-Elkhair, Heba Abdo Basha, Walaa Slouma Hamouda Abd El Naby, Jamaan S. Ajarem, Saleh N. Maodaa, Ahmed A. Allam, Mohammed A. E. Naiel
Animals.2020; 10(5): 809. CrossRef - Hair cortisol and dehydroepiandrosterone concentrations: Associations with executive function in early childhood
Ella-Marie P. Hennessey, Olga Kepinska, Stephanie L. Haft, Megan Chan, Isabel Sunshine, Chloe Jones, Roeland Hancock, Fumiko Hoeft
Biological Psychology.2020; 155: 107946. CrossRef - Sound characterization and fine-scale spatial mapping of an estuarine soundscape in the southeastern USA
C Mueller, A Monczak, J Soueidan, B McKinney, S Smott, T Mills, Y Ji, EW Montie
Marine Ecology Progress Series.2020; 645: 1. CrossRef - Key Factors Influencing Multimodal Transportation of Natural Block Rubber in Thailand
Pimnapa Pongsayaporn, Thanwadee Chinda, Veeris Ammarapala, L. Nazarko, J.-P. Pantouvakis, B.T. Kalsaas, C.-H. Ko
MATEC Web of Conferences.2020; 312: 02008. CrossRef - Repetitive Negative Thinking outperforms loneliness and lack of social connectedness as a predictor of prospective depressive symptoms in adolescents
Filip Raes, Margot Bastin, Tina Pede, Eline Belmans, Luc Goossens, Janne Vanhalst
Scandinavian Journal of Child and Adolescent Psychiatry and Psychology.2020; 8(1): 149. CrossRef - Existence of Integrated Regulation and Its Implication on Foreign Language Teaching: A Survey Study
Jing Yu
Innovation in Language Learning and Teaching.2020; 14(1): 67. CrossRef - Effectiveness of Workshop on Hand Washing Techniques among Undergraduate Nursing Students: A Quasi Experimental Study
Noor Asikime Binti Mohamad, Kasmini Che Muda, Siti Nor Asiah Ab Khadir, Umiaziente Suchi, Regidor III Dioso
Edelweiss: Psychiatry Open Access.2020; : 10. CrossRef - Short Sexual Well-Being Scale – a cross-sectional validation among transgender and cisgender people
Rafał Gerymski
Health Psychology Report.2020; 9(3): 276. CrossRef - Cognitive Distortions in Relation to Plasma Cortisol and Oxytocin Levels in Major Depressive Disorder
Susan Jennifer Thomas, Theresa Larkin
Frontiers in Psychiatry.2020;[Epub] CrossRef - AT HIGH BACKGROUND RADIATION AREAS THE RELATIONSHIP BETWEEN IN SITU INDOOR GAMMA DOSE RATES AND BUILDING MATERIALS: A CASE STUDY FROM ARIKLI VILLAGE (AYVACIK/ÇANAKKALE/TURKEY)
Gülcan Top, Yüksel Örgün, Gürsel Karahan, Orkan Özcan, Mark Horvath, Györgyi Kampfl
Radiation Protection Dosimetry.2020; 188(2): 246. CrossRef - Effects of Spirituality, Knowledge, Attitudes, and Practices toward Anxiety Regarding COVID-19 among the General Population in INDONESIA: A Cross-Sectional Study
Yohanes Andy Rias, Yafi Sabila Rosyad, Roselyn Chipojola, Bayu Satria Wiratama, Cikra Ikhda Safitri, Shuen Fu Weng, Chyn Yng Yang, Hsiu Ting Tsai
Journal of Clinical Medicine.2020; 9(12): 3798. CrossRef - The development of intestinal dysbiosis in anemic preterm infants
Thao T. B. Ho, Ambuj Kumar, Adetola F. Louis-Jacques, Larry J. Dishaw, Alyson L. Yee, Maureen W. Groer
Journal of Perinatology.2020; 40(7): 1066. CrossRef - INFLUENCE OF DIABETIC NEUROPATHY ON GAIT COMPLEXITY
Vanessa Raquel Metz, Rodrigo Maciel Andrade, Adriana Machado-Lima, Alberto Carlos Amadio, Júlio Cerca Serrão, Julia Maria D'Andréa Greve, Angélica Castilho Alonso
Revista Brasileira de Medicina do Esporte.2020; 26(5): 431. CrossRef - Theory of medical scoring systems and a practical method to evaluate Asian elephant (Elephas maximus) foot health in European zoos
N Ertl, P Wendler, E Sós, M Flügger, F Schneeweis, C Schiffmann, J-M Hatt, M Clauss
Animal Welfare.2020; 29(2): 163. CrossRef - Effects of Peer Encouragement on Efficacy Perceptions and Physical Performance in Children
Kira L. Innes, Jeffrey D. Graham, Steven R. Bray
Journal of Sport and Exercise Psychology.2020; 42(4): 314. CrossRef - Parametric or Non-parametric: Skewness to Test Normality for Mean Comparison
Fatih ORCAN
International Journal of Assessment Tools in Education.2020; 7(2): 255. CrossRef - EEMCO Guidance for the in vivo Assessment of Biomechanical Properties of the Human Skin and Its Annexes: Revisiting Instrumentation and Test Modes
Luis Monteiro Rodrigues, Joachim W. Fluhr
Skin Pharmacology and Physiology.2020; 33(1): 44. CrossRef - Scheduling Two Identical Parallel Machines Subjected to Release Times, Delivery Times and Unavailability Constraints
Adel M. Al-Shayea, Mustafa Saleh, Moath Alatefi, Mageed Ghaleb
Processes.2020; 8(9): 1025. CrossRef - Investigation of the factorial structure and psychometrics of the German version of the Florida Shock Anxiety Scale
Desiree Ritzka, Christian Petzold, Nadine Wäßnig, Bjarne Schmalbach, Katja Petrowski
Psychology, Health & Medicine.2020; 25(3): 344. CrossRef - To what degree and how do healthcare professionals in nursing homes and homecare practice user involvement? A mixed methods study
Eline Ree, Siri Wiig, Jeffrey Braithwaite, Ingunn Aase
Tidsskrift for omsorgsforskning.2020; 6(2): 119. CrossRef - Drawing a Sample with Desired Properties from Population in R Package “drawsample”
Kübra ATALAY KABASAKAL, Tuba GÜNDÜZ
Eğitimde ve Psikolojide Ölçme ve Değerlendirme Dergisi.2020; 11(4): 405. CrossRef - Monochloramine Formation and Decay in the Presence of H2O2 after UV/H2O2 Advanced Oxidation
Chengjin Wang, Liang Zheng, Susan Andrews, Ron Hofmann
Journal of Environmental Engineering.2020;[Epub] CrossRef - Automatic segmentation of liver/kidney area with double-layered fuzzy C-means and the utility of hepatorenal index for fatty liver severity classification
Kwang Baek Kim, Gwang Ha Kim, Doo Heon Song, Hyun Jun Park, Chang Won Kim
Journal of Intelligent & Fuzzy Systems.2020; 39(1): 925. CrossRef - Neighborhood crime, socioeconomic status, and suspiciousness in adolescents and young adults at Clinical High Risk (CHR) for psychosis
Teresa Vargas, Pamela J. Rakhshan Rouhakhtar, Jason Schiffman, Denise S. Zou, Kelsey J. Rydland, Vijay A. Mittal
Schizophrenia Research.2020; 215: 74. CrossRef - An epidemiological study of sleep−wake timings in school children from 4 to 11 years old: insights on the sleep phase shift and implications for the school starting times' debate
Maria Inês Clara, Ana Allen Gomes
Sleep Medicine.2020; 66: 51. CrossRef - The Moderating Role of Hope in the Relationship Between Maladaptive Perfectionism and Anxiety Among Early Adolescents
Ali Karababa
The Journal of Genetic Psychology.2020; 181(2-3): 159. CrossRef - Why tourists engage in online collective actions in times of crisis: Exploring the role of group relative deprivation
Xueting Zhai, Qiuju Luo, Long Wang
Journal of Destination Marketing & Management.2020; 16: 100414. CrossRef - The impact of personality traits on medication adherence and self-care in patients with type 2 diabetes mellitus: The moderating role of gender and age
Zahra Hazrati-Meimaneh, Mohammadali Amini-Tehrani, Ata Pourabbasi, Zabihollah Gharlipour, Fatemeh Rahimi, Parisa Ranjbar-Shams, Ensieh Nasli-Esfahani, Hadi Zamanian
Journal of Psychosomatic Research.2020; 136: 110178. CrossRef - Obesity and cardiovascular risk among Sri Lankan adolescents: Association of adipokines with anthropometric indices of obesity and lipid profile
Thilini Abeyratne, Rasika Perera, Sharaine Fernando
Nutrition.2020; 78: 110942. CrossRef - Association Between a Functional Polymorphism in the Monoamine Oxidase A (MAOA) Gene and Both Emotional Coping Style and Neuroticism
Diego A. Forero, Ana Adan, Sandra Lopez-Leon
The Open Neurology Journal.2020; 14(1): 10. CrossRef - Enumerating the phytic acid content in maize germplasm and formulation of reference set to enhance the breeding for low phytic acid
J. Lydia Pramitha, A. John Joel, Srisaila Srinivas, R. Sreeja, Firoz Hossain, R. Ravikesavan
Physiology and Molecular Biology of Plants.2020; 26(2): 353. CrossRef - Comorbid pain experiences in young women with dysmenorrhea
Michelle M. Gagnon, Randa Elgendy
Women & Health.2020; 60(8): 946. CrossRef - Sex differences in the association between chronotype and risk of depression
Kyung Min Kim, Seung Min Han, Kyoung Heo, Won-Joo Kim, Min Kyung Chu
Scientific Reports.2020;[Epub] CrossRef - Lipid oxidation inhibition capacity of plant extracts and powders in a processed meat model system
Stina C.M. Burri, Anders Ekholm, Uko Bleive, Tõnu Püssa, Martin Jensen, Jarkko Hellström, Sari Mäkinen, Risto Korpinen, Pirjo H. Mattila, Vitalijs Radenkovs, Dalija Segliņa, Åsa Håkansson, Kimmo Rumpunen, Eva Tornberg
Meat Science.2020; 162: 108033. CrossRef - Consistent Exposure to Psychosocial Stressors and Progressive Intolerance to Stress in Individuals at Clinical High Risk for Psychosis
Ivanka Ristanovic, Teresa Vargas, Henry R Cowan, Vijay Anand Mittal
Schizophrenia Bulletin Open.2020;[Epub] CrossRef - High precision strike point control to support experiments in the DIII-D small angle slot divertor
D. Eldon, A.W. Hyatt, B. Covele, N. Eidietis, H.Y. Guo, D.A. Humphreys, A.L. Moser, B. Sammuli, M.L. Walker
Fusion Engineering and Design.2020; 160: 111797. CrossRef - The relation between religiosity dimensions and support for interreligious conflict in Indonesia
Tery Setiawan, Edwin BP De Jong, Peer LH Scheepers, Carl JA Sterkens
Archive for the Psychology of Religion.2020; 42(2): 244. CrossRef - Impact of Parents’ Knowledge about the Development of Self-Esteem in Adolescents and Their Parenting Practice on the Self-Esteem and Suicidal Behavior of Urban High School Students in Nepal
Ratna Shila Banstola, Tetsuya Ogino, Sachiko Inoue
International Journal of Environmental Research and Public Health.2020; 17(17): 6039. CrossRef - Profiles of adolescent leisure motivation and substance use in the HealthWise South Africa research trial: a person-centered approach
Elizabeth H. Weybright, Lori-Ann Palen, Linda L. Caldwell, Lisa Wegner, Joachim J. Jacobs, Edward Smith
Leisure Sciences.2020; 42(5-6): 482. CrossRef - Quality of Life in Heterogeneous Anxiety Disorders: Changes Across Cognitive-Behavioral Treatments
Julianne G. Wilner, Steven Dufour, Katherine Kennedy, Shannon Sauer-Zavala, Hannah Boettcher, Todd J. Farchione, David H. Barlow
Behavior Modification.2020; 44(3): 343. CrossRef - Psychometric analyses of the Bangla version of the Dark Triad Dirty Dozen
Oli Ahmed, Lutfun Naher, Rohmotul Islam, Moslima Akter, Shila Deb
Heliyon.2020; 6(11): e05341. CrossRef - Risk Perception on Haze Pollution and Willingness to Pay for Self-Protection and Haze Management in Chiang Mai Province, Northern Thailand
Sukanya Sereenonchai, Noppol Arunrat, Duangporn Kamnoonwatana
Atmosphere.2020; 11(6): 600. CrossRef - Synergistic Effect of Low Neutrophil–Lymphocyte Ratio With Physical Activity on Quality of Life in Type 2 Diabetes Mellitus: A Community-Based Study
Yohanes Andy Rias, Maria Dyah Kurniasari, Victoria Traynor, Shu Fen Niu, Bayu Satria Wiratama, Ching Wen Chang, Hsiu Ting Tsai
Biological Research For Nursing.2020; 22(3): 378. CrossRef - Spatial Variability of Yield and Nitrogen Indicators—A Crop Rotation Approach
Remigiusz Łukowiak, Witold Grzebisz, Jakub Ceglarek, Adam Podolski, Cezary Kaźmierowski, Jan Piekarczyk
Agronomy.2020; 10(12): 1959. CrossRef - Effects of Safety Climate and Safety Behavior on Safety Outcomes between Supervisors and Construction Workers
Changquan He, Brenda McCabe, Guangshe Jia, Jide Sun
Journal of Construction Engineering and Management.2020;[Epub] CrossRef - Validation of the care providers version of the Rainbow Model of Integrated Care-measurement tool in Chinese primary care systems
Yixiang Huang, Paiyi Zhu, Lijin Chen, Xin Wang, Pim Valentijn
BMC Health Services Research.2020;[Epub] CrossRef - A Derivation of Factors Influencing the Diffusion and Adoption of an Open Source Learning Platform
Chi-Yo Huang, Hui-Ya Wang, Chia-Lee Yang, Steven J. H. Shiau
Sustainability.2020; 12(18): 7532. CrossRef - Investigating Preservice Middle School Mathematics Teachers’ Competencies in Statistics and Probability in Terms of Various Variables
Okan KUZU, Muhammet ARICAN
Eğitimde ve Psikolojide Ölçme ve Değerlendirme Dergisi.2020; 11(1): 13. CrossRef - Morningness-eveningness, relationship quality, and quality of life among couples living together
Zsuzsanna Tanyi, Veronika Mészáros, Máté Smohai, Edit Jakubovits, Andrea Ferenczi, Ilona Szili, Dóra Kovács, Zsuzsanna Kövi
Chronobiology International.2020; 37(12): 1736. CrossRef - Norm values and psychometric properties for the German health regulatory focus scale – results of a representative survey
Bjarne Schmalbach, Markus Zenger, Elmar Brähler, Katja Petrowski
BMC Medical Research Methodology.2020;[Epub] CrossRef - An analysis of mathematical literacy of state junior high school students in Kupang
D W Fointuna, A H Kaluge, A J Fernandez
Journal of Physics: Conference Series.2020; 1422(1): 012025. CrossRef - Phonological specificity relates to phonological awareness and reading ability in English–French bilingual children
Klaudia Krenca, Eliane Segers, Xi Chen, Sharry Shakory, Jeffrey Steele, Ludo Verhoeven
Reading and Writing.2020; 33(2): 267. CrossRef - The impact of food neophobia and sensation seeking of foreign tourists on the purchase intention of traditional Turkish food
Kadri Koray Sivrikaya, Yeliz Pekerşen
International Journal of Gastronomy and Food Science.2020; 21: 100222. CrossRef - Physiological changes during prolonged standing and walking considering age, gender and standing work experience
Rudolf Wall, Gabriela Garcia, Thomas Läubli, Robert Seibt, Monika A. Rieger, Bernard Martin, Benjamin Steinhilber
Ergonomics.2020; 63(5): 579. CrossRef - Validation of a translated internet gaming disorder scale (short form) and measurement invariance across sex groups in Malaysian samples
Soo Ting T’ng, Kee Pau
Current Psychology.2020; 39(6): 1977. CrossRef - Sex differences in muscle activity and motor variability in response to a non-fatiguing repetitive screwing task
Tessy Luger, Robert Seibt, Monika A. Rieger, Benjamin Steinhilber
Biology of Sex Differences.2020;[Epub] CrossRef - Herding in human groups is related to high autistic traits
I. Z. Marton-Alper, H. Z. Gvirts-Provolovski, M. Nevat, M. Karklinsky, S. G. Shamay-Tsoory
Scientific Reports.2020;[Epub] CrossRef - Tour member fit and tour member–leader fit on group package tours: Influences on tourists’ positive emotions, rapport, and satisfaction
Shu-Yun Chang, Sheng-Hshiung Tsaur, Chang-Hua Yen, Hung-Ru Lai
Journal of Hospitality and Tourism Management.2020; 42: 235. CrossRef - Increased and More Heterogeneous Gadoxetic Acid Uptake of the Liver Parenchyma after Hepatitis C Virus Eradication by Direct Antiviral Agent
Nobuhiro Fujita, Akihiro Nishie, Yoshiki Asayama, Kousei Ishigami, Tomohiro Nakayama, Yasuhiro Ushijima, Daisuke Kakihara, Yukihisa Takayama, Koichiro Morita, Keisuke Ishimatsu, Seiichiro Takao, Tomoharu Yoshizumi, Norihiro Furusyo, Hiroshi Honda
Magnetic Resonance in Medical Sciences.2020; 19(4): 389. CrossRef - Effects of measurements on correlations of software code metrics
Md Abdullah Al Mamun, Christian Berger, Jörgen Hansson
Empirical Software Engineering.2019; 24(4): 2764. CrossRef - Empirical validation of a model predicting depression, anxiety, and stress in parents of children with autism
Scarlett Bones, Kimberley Norris, Michael Quinn
Clinical Psychologist.2019; 23(3): 249. CrossRef - Privacy, security, trust, risk and optimism bias in e-government use: The case of two Southern African Development Community countries
Willard Munyoka, Manoj S. Maharaj
SA Journal of Information Management.2019;[Epub] CrossRef - Cognitive and linguistic precursors of early first and second language reading development
Moniek M.H. Schaars, E. Segers, L. Verhoeven
Learning and Individual Differences.2019; 72: 1. CrossRef - Safety and efficacy of total intraluminal topical anaesthesia for ureteroscopy. Is success worth the pain?
J.S. Sandhu, Ajit K. Singh, Abhijit Bhatulkar, Uday Pratap, Milind Chauhan
Medical Journal Armed Forces India.2019; 75(2): 204. CrossRef - Development of a hearing help-seeking questionnaire based on the theory of planned behavior
Michelle Arnold, Brent J. Small, Kathryn Hyer, Theresa Chisolm, Melissa T. Frederick, ShienPei C. Silverman, Gabrielle H. Saunders
International Journal of Audiology.2019; 58(5): 287. CrossRef - Analyzing the influence of employee values on knowledge management in sport organizations
Vahid Delshab, Mathieu Winand, Saeed Sadeghi Boroujerdi, Do Young Pyun, Abed Mahmoudian
Journal of Science and Technology Policy Management.2019; 10(3): 667. CrossRef - Value of whole-liver apparent diffusion coefficient histogram analysis for quantification of liver fibrosis stages
Zhao-xia Yang, Xin-Xing Hu, Robert Grimm, Cai-xia Fu, Xu Yan, Meng-su Zeng, Sheng-Xiang Rao
Chinese Journal of Academic Radiology.2019; 1(1): 6. CrossRef - Self‐beliefs in organic chemistry: Evaluation of a reciprocal causation, cross‐lagged model
Rebecca E. Gibbons, Jeffrey R. Raker
Journal of Research in Science Teaching.2019; 56(5): 598. CrossRef - Can sustained attention adapt to prior cognitive effort? An evidence from experimental study
Anna Kamza, Marta Molińska, Nina Skrzypska, Piotr Długiewicz
Acta Psychologica.2019; 192: 181. CrossRef - Measurement Invariance of the Nine-Item Internet Gaming Disorder Scale (IGDS9-SF) Across Albania, USA, UK, and Italy
Valeria de Palo, Lucia Monacis, Maria Sinatra, Mark D. Griffiths, Halley Pontes, Menada Petro, Silvana Miceli
International Journal of Mental Health and Addiction.2019; 17(4): 935. CrossRef - Effects of Transparency and Controller Type on Performance in A Multi-Layer Display
Sarah C. Leibner, Alexandra Proaps, James P. Bliss
Proceedings of the Human Factors and Ergonomics Society Annual Meeting.2019; 63(1): 1772. CrossRef - Does work engagement mediate the influence of job resourcefulness on job crafting?
Chien-Yu Chen
International Journal of Contemporary Hospitality Management.2019; 31(4): 1684. CrossRef - The Impact of Web-Based Ratings on Patient Choice of a Primary Care Physician Versus a Specialist: Randomized Controlled Experiment
Siyue Li, Austin Hubner
Journal of Medical Internet Research.2019; 21(6): e11188. CrossRef - Transdiagnostic Model of Anxiety and Depression According to the Relationship with Affect, Intolerance of Uncertainly, and Anxiety Sensitivity
Ronald Alberto Toro Tobar, Bertha Lucía Avendaño-Prieto, Nancy Vargas
Revista CES Psicología.2019; 13(1): 140. CrossRef - Relationship Between Aquifer Processes and Groundwater Quality: A Case of Olbanita Aquifer System, Lower Baringo Basin, Kenya Rift
Benjamin Sosi, Albert Getabu, Samson Maobe, Justus Barongo
Air, Soil and Water Research.2019;[Epub] CrossRef - Leveraging Means-Goal Associations to Boost Children’s Water Consumption: Persuasion in a Four-School, Three-Month Field Experiment
Szu-Chi Huang, Daniella Kupor, Michal Maimaran, Andrea Weihrauch
Journal of the Association for Consumer Research.2019; 4(1): 77. CrossRef - Semantic-Pragmatic Impairment in the Narratives of Children With Autism Spectrum Disorders
Naama Kenan, Ditza A. Zachor, Linda R. Watson, Esther Ben-Itzchak
Frontiers in Psychology.2019;[Epub] CrossRef - Adolescents’ production of complex syntax in spoken and written expository and persuasive genres
Danielle Brimo, Shannon Hall-Mills
Clinical Linguistics & Phonetics.2019; 33(3): 237. CrossRef - The roles of absorptive capacity and cultural balance for exploratory and exploitative innovation in SMEs
Everist Limaj, Edward W.N. Bernroider
Journal of Business Research.2019; 94: 137. CrossRef - The prevalence, nature, and functions of non-suicidal self-injury (NSSI) in a South African student sample
Sarojini Naidoo
South African Journal of Education.2019; 39(.): 1. CrossRef - The Role of Effortful Control in Stuttering Severity in Children: Replication Study
Shelly Jo Kraft, Emily Lowther, Janet Beilby
American Journal of Speech-Language Pathology.2019; 28(1): 14. CrossRef - Importance of Wellness Concepts in the Hotel Industry: Perspectives from the Millennials
Patrick C. Lee, Myong Jae Lee, Ting-Ting Cheng
Journal of Quality Assurance in Hospitality & Tourism.2019; 20(6): 729. CrossRef - Understanding problematic eating in out-of-home care: The role of attachment and emotion regulation
Anna Norrish, Rachael Cox, Angela Simpson, Heidi Bergmeier, Lauren Bruce, Melissa Savaglio, Bengianni Pizzirani, Renee O'Donnell, Madelaine Smales, Helen Skouteris
Appetite.2019; 135: 33. CrossRef - Calibration and Statistical Performance of Al2O3:C Optically Stimulated Luminescent Dosimeters With and Without Annealing Using a 137Cs Source
Kevin Liu, Robert M. Golduber, David J. Trimas, Sara A. Abraham, Logan V. Latosz, Jasmine L. Mapes, Jonathan M. Miller, Kimberlee J. Kearfott
Health Physics.2019; 116(1): 42. CrossRef - Falling in love with a place because of a song: the transportation effects of music on place attachment
Yuanyuan Chen, Peixue Liu, Jianxin Zhang, Xiao Xiao
Asia Pacific Journal of Tourism Research.2019; 24(9): 882. CrossRef - The Impact of Deep Brain Stimulation for Parkinson’s Disease on Couple Satisfaction: An 18-Month Longitudinal Study
Marc Baertschi, Nicolas Favez, João Flores Alves Dos Santos, Michalina Radomska, François Herrmann, Pierre Burkhard, Alessandra Canuto, Kerstin Weber
Journal of Clinical Psychology in Medical Settings.2019; 26(4): 461. CrossRef - Prostate Cancer Detection using Deep Convolutional Neural Networks
Sunghwan Yoo, Isha Gujrathi, Masoom A. Haider, Farzad Khalvati
Scientific Reports.2019;[Epub] CrossRef - Psychometric properties and validation of the Polish adaptation of the Light Triad Scale
Rafał Gerymski, Dariusz Krok
Current Issues in Personality Psychology.2019; 7(4): 341. CrossRef - Repositioning sales as an influence on innovation and a source of sustainable competitive advantage
Ovidiu-Iulian Bunea
Proceedings of the International Conference on Business Excellence.2019; 13(1): 492. CrossRef - Enhancing student competency in risky clinical environments: Evaluating an online education program
Ella Graj, Jade Sheen, Amanda Dudley, Wendy Sutherland‐smith, Jane Mcgillivray
Australian Psychologist.2019; 54(1): 68. CrossRef - Late-onset hypogonadism (LOH), masculinity and relationship and sexual satisfaction: are sexual symptoms of LOH mediators of traditional masculinity on relationship and sexual satisfaction?
P. A. Costa, I. Q. Garcia, F. Pimenta, J. Marôco, I. Leal
Sexual Health.2019; 16(4): 389. CrossRef - Increased psychiatric symptoms in university students with autism spectrum disorder are associated with reduced adaptive behavior
Gil Zukerman, Gili Yahav, Ester Ben-Itzchak
Psychiatry Research.2019; 273: 732. CrossRef - Propriedades psicométricas da Frontal Assessment Battery na esclerose múltipla
Sandra Henriques, Helena Espirito-Santo, Luís Cunha, Laura Lemos, Fernanda Daniel
Revista Portuguesa de Investigação Comportamental e Social.2019; 5(2): 19. CrossRef - Knowledge of Autism for Parents of Low Income with Low Literacy: Description and Relationship to Child Development Knowledge
Jonathan M. Campbell, Daphne Greenberg, Peggy A. Gallagher, Zolinda Stoneman, Christina Simmons
Advances in Neurodevelopmental Disorders.2019; 3(1): 8. CrossRef - Multi-Scale Assessment of Relationships between Fragmentation of Riparian Forests and Biological Conditions in Streams
Yirigui Yirigui, Sang-Woo Lee, A. Pouyan Nejadhashemi
Sustainability.2019; 11(18): 5060. CrossRef - Neurophysics Assessment of the Muscle Bioenergy Generated by Transcranial Magnetic Stimulation
Fidias E. Leon-Sarmiento, Alexander Gonzalez-Castaño, Carlos V. Rizzo-Sierra, Juan Aceros, Daniel S. Leon-Ariza, Juan S. Leon-Ariza, Diddier G. Prada, William Bara-Jimenez, Zeng Y. Wang
Research.2019;[Epub] CrossRef - Assessing Developmental Environmental Risk Factor Exposure in Clinical High Risk for Psychosis Individuals: Preliminary Results Using the Individual and Structural Exposure to Stress in Psychosis-Risk States Scale
Teresa Vargas, Denise S. Zou, Rachel E. Conley, Vijay A. Mittal
Journal of Clinical Medicine.2019; 8(7): 994. CrossRef - Impact of applying different resting blood pressure cut-points to clear for maximal exercise
Elizabeth B. Yee, Alison Macpherson, Norman Gledhill, Scott Gledhill, Veronica Jamnik, Gemma S. Milligan, Sam D. Blacker, Pieter E.H. Brown, Andrew G. Siddall
Work.2019; 63(4): 635. CrossRef - Validation of a Limitations in Daily Activities Scale for Chronic Pain
Keith G. Wilson, Dyana Castillo, John Kowal, An Gie Yong, Lachlan A. McWilliams
The Journal of Pain.2019; 20(1): 68. CrossRef - Associations of Acculturation with English- and Spanish-Language Health Literacy Among Bilingual Latino Adults
Ashley J. Housten, Diana Stewart Hoover, Virmarie Correa-Fernández, Larkin L. Strong, Whitney L. Heppner, Christine Vinci, David W. Wetter, Claire A. Spears, Yessenia Castro
HLRP: Health Literacy Research and Practice.2019;[Epub] CrossRef - Is There a Relationship between Transepidermal Water Loss and Microbial Biodiversity on the Skin?
Christopher Wallen-Russell
Cosmetics.2019; 6(1): 18. CrossRef - Influence of a passive lower-limb exoskeleton during simulated industrial work tasks on physical load, upper body posture, postural control and discomfort
Tessy Luger, Robert Seibt, Timothy J. Cobb, Monika A. Rieger, Benjamin Steinhilber
Applied Ergonomics.2019; 80: 152. CrossRef - Problem-Solving Ability and Stress Mediate the Relationship Between Creativity and Happiness
Chee-Seng Tan, Soon-Aun Tan, Intan Hashimah Mohd Hashim, Mah-Ngee Lee, Anna Wen-Huey Ong, Siti nor Binti Yaacob
Creativity Research Journal.2019; 31(1): 15. CrossRef - Maladaptive beliefs as mediators of the relationship between personality traits and Borderline Personality Disorder symptoms
Renata SALDANHA-SILVA, Fabio Luiz NUNES, Helga Alessandra de REZENDE, Marcela MANSUR-ALVES
Estudos de Psicologia (Campinas).2019;[Epub] CrossRef - Esophageal feeding tube placement and the associated complications in 248 cats
Craig R. Breheny, Alisdair Boag, Alice Le Gal, Sven‐Erik Hõim, Matteo Cantatore, Davina Anderson, Tim Nuttall, Marjoie L. Chandler, Danièlle A. Gunn‐Moore
Journal of Veterinary Internal Medicine.2019; 33(3): 1306. CrossRef - Telomere length and childhood trauma in Colombians with depressive symptoms
Karen M. Jiménez, Angela J. Pereira-Morales, Ana Adan, Diego A. Forero
Brazilian Journal of Psychiatry.2019; 41(3): 194. CrossRef - Neurophysics Assessment of the Muscle Bioenergy Generated by Transcranial Magnetic Stimulation
Fidias E. Leon-Sarmiento, Alexander Gonzalez-Castaño, Carlos V. Rizzo-Sierra, Juan Aceros, Daniel S. Leon-Ariza, Juan S. Leon-Ariza, Diddier G. Prada, William Bara-Jimenez, Zeng Y. Wang
Research.2019; 2019: 1. CrossRef - The Impact of a Schoolwide Mindfulness Program on Adolescent Well-Being, Stress, and Emotion Regulation: A Nonrandomized Controlled Study in a Naturalistic Setting
Andrew J. Campbell, Richard P. Lanthier, Brandi A. Weiss, Megan D. Shaine
Journal of Child and Adolescent Counseling.2019; 5(1): 18. CrossRef - Aortic and Systemic Arterial Stiffness Responses to Acute Exercise in Patients With Small Abdominal Aortic Aneurysms
Maria Perissiou, Tom G. Bailey, Mark Windsor, Kim Greaves, Michael C.Y. Nam, Fraser D. Russell, Jill O'Donnell, Rebecca Magee, Pankaj Jha, Karl Schulze, Anthony S. Leicht, Jonathan Golledge, Christopher D. Askew
European Journal of Vascular and Endovascular Surgery.2019; 58(5): 708. CrossRef - NEDEN KULLANICILAR TWITCH TV ÜZERİNDE YAYINCILARA BAĞIŞ YAPAR? TWITCH TV KULLANICILARI ÜZERİNDE AMPİRİK BİR ARAŞTIRMA
Alper Hakan YAVAŞÇALI, Yusuf Zafer Can UĞURHAN
Gümüşhane Üniversitesi İletişim Fakültesi Elektronik Dergisi.2019; 7(2): 646. CrossRef - The reliability and validity of the Chinese Short Warwick-Edinburgh Mental Well-being Scale in the general population of Hong Kong
Yuying Sun, Tzu Tsun Luk, Man Ping Wang, Chen Shen, Sai Yin Ho, Kasisomayajula Viswanath, Sophia Siu Chee Chan, Tai Hing Lam
Quality of Life Research.2019; 28(10): 2813. CrossRef - Different predictive and accuracy models for sex and stature estimation from second- and fourth-digit lengths in the Kinnaur population of Himachal Pradesh, North India: Medico-legal and forensic implications
Bahadur Singh, Kewal Krishan, Kawaljit Kaur, Tanuj Kanchan
Medicine, Science and the Law.2019; 59(3): 149. CrossRef - In situ statistical measurement of local morphology in carbon-epoxy composites using synchrotron X-ray computed tomography
Sebastian Rosini, Mark N. Mavrogordato, Olga Egorova, Emily S. Matthews, Samuel E. Jackson, S. Mark Spearing, Ian Sinclair
Composites Part A: Applied Science and Manufacturing.2019; 125: 105543. CrossRef - Examination and Validation of Classification Schema for Determining Thermal Taste Status
Margaret Thibodeau, Anthony Saliba, Martha Bajec, Gary Pickering
Chemosensory Perception.2019; 12(2): 69. CrossRef - Lowering consumers’ price image without lowering their internal reference price: the role of pay-what-you-want pricing mechanism
Rafael Luis Wagner
Journal of Revenue and Pricing Management.2019; 18(4): 332. CrossRef - Comprehensive measurement of health system performance at district level in India: Generation of a composite index
Atul Sharma, Shankar Prinja, Arun Kumar Aggarwal
The International Journal of Health Planning and Management.2019;[Epub] CrossRef - Distinguishing soft tissue sarcomas of different histologic grades based on quantitative MR assessment of intratumoral heterogeneity
Pei Xiang, Xiaoling Zhang, Dawei Liu, Chaoyang Wang, Lei Ding, Fen Wang, Zhaohui Zhang
European Journal of Radiology.2019; 118: 194. CrossRef - In Vivo Restoration of Myocardial Conduction With Carbon Nanotube Fibers
Mark D. McCauley, Flavia Vitale, J. Stephen Yan, Colin C. Young, Brian Greet, Marco Orecchioni, Srikanth Perike, Abdelmotagaly Elgalad, Julia A. Coco, Mathews John, Doris A. Taylor, Luiz C. Sampaio, Lucia G. Delogu, Mehdi Razavi, Matteo Pasquali
Circulation: Arrhythmia and Electrophysiology.2019;[Epub] CrossRef - Response suppression, strategy application, and working memory in the prediction of academic performance and classroom misbehavior: A neuropsychological approach
Graham Pluck, David Villagomez-Pacheco, María Isabel Karolys, María Emilia Montaño-Córdova, Pamela Almeida-Meza
Trends in Neuroscience and Education.2019; 17: 100121. CrossRef - Perceived Stress as a Mediator of the Relationship between Neuroticism and Depression and Anxiety Symptoms
Angela J. Pereira-Morales, Ana Adan, Diego A. Forero
Current Psychology.2019; 38(1): 66. CrossRef - Comparing the Mullen Scales of Early Learning and the Preschool Language Scale—Fifth Edition for Young Children with Autism Spectrum Disorder
Emma Riley, Jessica Paynter, Linda Gilmore
Advances in Neurodevelopmental Disorders.2019; 3(1): 29. CrossRef - Revisiting the Relationship Between Acculturation and Smoking Cessation Among Mexican Americans
Yessenia Castro, Christine Vinci, Whitney L Heppner, Miguel Ángel Cano, Virmarie Correa-Fernández, David W Wetter
Annals of Behavioral Medicine.2019; 53(3): 211. CrossRef - FANCM, RAD1, CHEK1 and TP53I3 act as BRCA-like tumor suppressors and are mutated in hereditary ovarian cancer
Jaime L. Lopes, Sophia Chaudhry, Guilherme S. Lopes, Nancy K. Levin, Michael A. Tainsky
Cancer Genetics.2019; 235-236: 57. CrossRef - A Neurophysiological and Behavioral Assessment of Interventions Targeting Attention Bias and Sense of Control in Binge Drinking
Jessica E. Langbridge, Richard D. Jones, Juan J. Canales
Frontiers in Human Neuroscience.2019;[Epub] CrossRef - Reliability analysis and removal efficiency relationship of common effluent treatment plants of industrial clusters
A. Padalkar, S. Kaur, R. Kumar
International Journal of Environmental Science and Technology.2019; 16(3): 1379. CrossRef - Parent help-seeking behaviour: Examining the impact of parent beliefs on professional help-seeking for child emotional and behavioural difficulties
Jennah Alonso, Emma Little
The Educational and Developmental Psychologist.2019; 36(2): 60. CrossRef - Lipid Oxidation Inhibition Capacity of 11 Plant Materials and Extracts Evaluated in Highly Oxidised Cooked Meatballs
Stina C. M. Burri, Kajsa Granheimer, Marine Rémy, Anders Ekholm, Åsa Håkansson, Kimmo Rumpunen, Eva Tornberg
Foods.2019; 8(9): 406. CrossRef - Automatic detection, classification, and quantification of sciaenid fish calls in an estuarine soundscape in the Southeast United States
Agnieszka Monczak, Yiming Ji, Jamileh Soueidan, Eric W. Montie, Craig A. Radford
PLOS ONE.2019; 14(1): e0209914. CrossRef - Time-lapse imaging reveals delayed development of embryos carrying unbalanced chromosomal translocations
Hadar Amir, Shiri Barbash-Hazan, Yael Kalma, Tsvia Frumkin, Mira Malcov, Nivin Samara, Joseph Hasson, Adi Reches, Foad Azem, Dalit Ben-Yosef
Journal of Assisted Reproduction and Genetics.2019; 36(2): 315. CrossRef - Sound patterns of snapping shrimp, fish, and dolphins in an estuarine soundscape of the southeastern USA
A Monczak, C Mueller, ME Miller, Y Ji, SA Borgianini, EW Montie
Marine Ecology Progress Series.2019; 609: 49. CrossRef - Reliability and validity of a Central Kurdish version of the Dizziness Handicap Inventory
Sherko Saeed F. Zmnako, Yousif Ibrahim Chalabi
Scientific Reports.2019;[Epub] CrossRef - Sarcopenia Is Associated with Postoperative Outcome in Patients with Crohn’s Disease Undergoing Bowel Resection
Diogo Carvalho, Charlene Viana, Isabel Marques, Catarina Costa, Sandra F. Martins
Gastrointestinal Disorders.2019; 1(1): 201. CrossRef - An intervention including the national early warning score improves patient monitoring practice and reduces mortality: A cluster randomized controlled trial
Filip Haegdorens, Koenraad G. Monsieurs, Koen De Meester, Peter Van Bogaert
Journal of Advanced Nursing.2019; 75(9): 1996. CrossRef - The relations between YouTube addiction, social anxiety and parasocial relationships with YouTubers: A moderated-mediation model based on a cognitive-behavioral framework
Pierre de Bérail, Marlène Guillon, Catherine Bungener
Computers in Human Behavior.2019; 99: 190. CrossRef - Cognitive predictors of word reading in Sinhala
M. A. D. K. Wijaythilake, R. Parrila, Tomohiro Inoue, Sonali Nag
Reading and Writing.2019; 32(7): 1881. CrossRef - Creativity in the acquisition of computational thinking
Arnon Hershkovitz, Raquel Sitman, Rotem Israel-Fishelson, Andoni Eguíluz, Pablo Garaizar, Mariluz Guenaga
Interactive Learning Environments.2019; 27(5-6): 628. CrossRef - Are changes in children's communication patterns predictive of treatment outcomes for children with anxiety?
Anna Lichtwarck‐Aschoff, Marieke M.J.W. van Rooij
Clinical Psychology & Psychotherapy.2019; 26(5): 572. CrossRef - Determining the Generalizability of the PROMIS Depression Domain’s Floor Effect and Completion Time in Patients Undergoing Orthopaedic Surgery
David N. Bernstein, Joshua Atkinson, Kathleen Fear, Judith F. Baumhauer, Addisu Mesfin, Paul T. Rubery, Warren C. Hammert
Clinical Orthopaedics & Related Research.2019; 477(10): 2215. CrossRef - Small-scale postharvest practices among plantain farmers and traders: A potential for reducing losses in rivers state, Nigeria
Kwami Justina Morris, Nitty Hirawaty Kamarulzaman, Kenobi Isima Morris
Scientific African.2019; 4: e00086. CrossRef - The Association Between Diabetes and Cognitive Function in Later Life
Yadollah A. Momtaz, Tengku A. Hamid, Mohamad F. Bagat, Maryam Hazrati
Current Aging Science.2019; 12(1): 62. CrossRef - Assessing Change Over Time in Voice Handicap and Voice-Related Perceived Control Using Ecological Momentary Assessment
Viann N. Nguyen-Feng, Patricia A. Frazier, Ali Stockness, Scott Lunos, Alexis N. Hoedeman, Stephanie Misono
Annals of Otology, Rhinology & Laryngology.2019; 128(9): 829. CrossRef - Fear of Missing Out and Relational Aggression on Facebook
Loren Abell, Sarah L. Buglass, Lucy R. Betts
Cyberpsychology, Behavior, and Social Networking.2019; 22(12): 799. CrossRef - Preclinical Evidence Supporting Early Initiation of Citalopram Treatment in Machado-Joseph Disease
Sofia Esteves, Stéphanie Oliveira, Sara Duarte-Silva, Daniela Cunha-Garcia, Andreia Teixeira-Castro, Patrícia Maciel
Molecular Neurobiology.2019; 56(5): 3626. CrossRef - Comparison of surgically induced astigmatism (SIA) values using three Holladay incorporated method SIA calculators
M M Md Muziman Syah, M Nurul Adabiah, A H Noorhazayti, M Nazaryna, M Azuwan, M Noryanti, C A Mohd Zulfaezal, B Noor Ezailina
Journal of Physics: Conference Series.2019; 1366(1): 012053. CrossRef - Identification of novel urease inhibitors: pharmacophore modeling, virtual screening and molecular docking studies
Richa Arora, Upasana Issar, Rita Kakkar
Journal of Biomolecular Structure and Dynamics.2019; 37(16): 4312. CrossRef - Effect of Educational Program on Knowledge, Attitude, and Willingness of Nursing Students for Hematopoietic Stem-Cell Donation
Miok Kim, Minho Shin
International Journal of Environmental Research and Public Health.2019; 16(19): 3696. CrossRef - A Contribution to Validation of the Short Schema Mode Inventory in an Italian Clinical Versus Non-clinical Population
Marta Panzeri, Lilybeth Fontanesi, Chiara Busà, Alessandro Carmelita, Lucia Ronconi, Harold Dadomo
Journal of Rational-Emotive & Cognitive-Behavior Therapy.2019; 37(2): 149. CrossRef - Primary music teachers’ efficacy in Hong Kong’s inclusive classrooms
Marina Wai-yee Wong, Edmund Sze Shing Chan, Maria Pik-yuk Chik
Music Education Research.2019; 21(5): 517. CrossRef - Impacto na mortalidade da admissão direta versus transferência inter‐hospitalar nos doentes com enfarte agudo do miocárdio com elevação do segmento ST submetidos a intervenção coronária percutânea primária
Ana Sofia Ferreira, João Costa, Carlos Galvão Braga, Jorge Marques
Revista Portuguesa de Cardiologia.2019; 38(9): 621. CrossRef - Impact of psychological capital on construction worker safety behavior: Communication competence as a mediator
Changquan He, Guangshe Jia, Brenda McCabe, Yuting Chen, Jide Sun
Journal of Safety Research.2019; 71: 231. CrossRef - The Mediating Role of Creative Process Engagement in the Relationship between Shyness and Self‐Rated Creativity
Chee‐Seng Tan, Xiao‐Shan Lau, Ling‐Khai Lee
The Journal of Creative Behavior.2019; 53(2): 222. CrossRef - Characteristic and correlation analysis of influent and energy consumption of wastewater treatment plants in Taihu Basin
Luxi Zou, Huaibo Li, Shuo Wang, Kaikai Zheng, Yan Wang, Guocheng Du, Ji Li
Frontiers of Environmental Science & Engineering.2019;[Epub] CrossRef - Blood Pressure, Sexual Activity, and Erectile Function in Hypertensive Men: Baseline Findings from the Systolic Blood Pressure Intervention Trial (SPRINT)
Capri G. Foy, Jill C. Newman, Dan R. Berlowitz, Laurie P. Russell, Paul L. Kimmel, Virginia G. Wadley, Holly N. Thomas, Alan J. Lerner, William T. Riley
The Journal of Sexual Medicine.2019; 16(2): 235. CrossRef - Path analysis in Mplus: A tutorial using a conceptual model of psychological and behavioral antecedents of bulimic symptoms in young adults
Kheana Barbeau, Kayla Boileau, Fatima Sarr, Kevin Smith
The Quantitative Methods for Psychology.2019; 15(1): 38. CrossRef - Score Distributions of the Balance Outcome Measure for Elder Rehabilitation (BOOMER) in Community-Dwelling Older Adults With Vertebral Fracture
Zachary M. Brown, Jenna C. Gibbs, Jonathan D. Adachi, Maureen C. Ashe, Keith D. Hill, David L. Kendler, Aliya Khan, Alexandra Papaioannou, Sadhana Prasad, John D. Wark, Lora M. Giangregorio
Journal of Geriatric Physical Therapy.2019; 42(3): E87. CrossRef - Alexithymia, body mass index and gestational diabetes in pregnant women — FinnBrain birth cohort study
Jani Kajanoja, Max Karukivi, Noora M. Scheinin, Jetro J. Tuulari, Hanna Ahrnberg, Linnea Karlsson, Hasse Karlsson
Journal of Psychosomatic Research.2019; 124: 109742. CrossRef - Validation of High School Students’ Scores on the Revised Fit, Stigma, and Value Scale: Implications for School Counseling Screening
Michael Thomas Kalkbrenner, Emily Goodman-Scott, Edward Neukrug
Professional School Counseling.2019;[Epub] CrossRef - Rider factors associated with severe injury after a light motorcycle crash: A multicentre study in an emerging economy setting
Carlos Lam, Chih-Wei Pai, Chia-Chang Chuang, Yu-Chun Yen, Chia-Chieh Wu, Shih-Hsiang Yu, Kuo-Sheng Hung, Wen-Ta Chiu, Yanyong Guo
PLOS ONE.2019; 14(6): e0219132. CrossRef - Measuring the quality of dying and death in advanced cancer: Item characteristics and factor structure of the Quality of Dying and Death Questionnaire
Kenneth Mah, Sarah Hales, Isuri Weerakkody, Lucy Liu, Samantha Fernandes, Anne Rydall, Sigrun Vehling, Camilla Zimmermann, Gary Rodin
Palliative Medicine.2019; 33(3): 369. CrossRef - The Role of Motor Learning on Measures of Physical Requirements and Motor Variability During Repetitive Screwing
Tessy Luger, Robert Seibt, Monika A. Rieger, Benjamin Steinhilber
International Journal of Environmental Research and Public Health.2019; 16(7): 1231. CrossRef - Money shouts! How effective are punishments for accounting fraud?
Yang Wang, John K. Ashton, Aziz Jaafar
The British Accounting Review.2019; 51(5): 100824. CrossRef - Volunteer motivation, social problem solving,self-efficacy, and mental health: a structural equation model approach
Ying Lau, Lue Fang, Ling Jie Cheng, Ho Keung Dennis Kwong
Educational Psychology.2019; 39(1): 112. CrossRef - Cross-cultural adaptation, reliability, and validity of the Vertigo symptom scale–short form in the central Kurdish dialect
Sherko Saeed F. Zmnako, Yousif Ibrahim Chalabi
Health and Quality of Life Outcomes.2019;[Epub] CrossRef - Challenges of Research Collaboration in Ghana’s Knowledge-based Economy
Mavis Serwah Benneh Mensah, Francis Enu-Kwesi, Rosemond Boohene
Journal of the Knowledge Economy.2019; 10(1): 186. CrossRef - Stature estimation from different combinations of foot measurements using linear and multiple regression analysis in a North Indian male population
Bahadur Singh, Kewal Krishan, Kawaljit Kaur, Tanuj Kanchan
Journal of Forensic and Legal Medicine.2019; 62: 25. CrossRef - Mood rhythmicity is associated with depressive symptoms and caffeinated drinks consumption in South American young adults
Angela J. Pereira-Morales, Leandro P. Casiraghi, Ana Adan, Andrés Camargo
Chronobiology International.2019; 36(2): 225. CrossRef - Tools for Measuring Construction Materials Management Practices and Predicting Labor Productivity in Multistory Building Projects
Argaw Tarekegn Gurmu
Journal of Construction Engineering and Management.2019;[Epub] CrossRef - Illness Perception as a Predictor of Foot Care Behavior Among People With Type 2 Diabetes Mellitus in Indonesia
Sofyan Indrayana, Su-Er Guo, Ching-Lan Lin, Su-Ying Fang
Journal of Transcultural Nursing.2019; 30(1): 17. CrossRef - Usefulness of Modern Activity Trackers for Monitoring Exercise Behavior in Chronic Cardiac Patients: Validation Study
Cyrille Herkert, Jos Johannes Kraal, Eline Maria Agnes van Loon, Martijn van Hooff, Hareld Marijn Clemens Kemps
JMIR mHealth and uHealth.2019; 7(12): e15045. CrossRef - Infant Food Security in New Zealand: A Multidimensional Index Developed from Cohort Data
Deborah Schlichting, Ladan Hashemi, Cameron Grant
International Journal of Environmental Research and Public Health.2019; 16(2): 283. CrossRef - Weight loss is associated with improved quality of life among rural women completers of a web-based lifestyle intervention
Patricia A. Hageman, Joseph E. Mroz, Michael A. Yoerger, Carol H. Pullen, Maciej S. Buchowski
PLOS ONE.2019; 14(11): e0225446. CrossRef - Hospitals’ use of hospitalists: Implications for financial performance
Josué Patien Epané, Robert Weech-Maldonado, Larry Hearld, Nir Menachemi, Bisakha Sen, Stephen O’Connor, Zo Ramamonjiarivelo
Health Care Management Review.2019; 44(1): 10. CrossRef - The mechanism of tourism slogans on travel intention based on Unique Selling Proposition (USP) theory
Ying Wang, Li Huang, Jixin Li, Yang Yang
Journal of Travel & Tourism Marketing.2019; 36(4): 415. CrossRef - The Influence of Race-Related Stress on Eating Pathology: The Mediating Role of Depression and Moderating Role of Cultural Worldview Among Black American Women
Temilola K. Salami, Sierra E. Carter, Blaine Cordova, Kelci C. Flowers, Rheeda L. Walker
Journal of Black Psychology.2019; 45(6-7): 571. CrossRef - Impact on mortality of direct admission versus interhospital transfer in patients with ST-segment elevation myocardial infarction undergoing primary percutaneous coronary intervention
Ana Sofia Ferreira, João Costa, Carlos Galvão Braga, Jorge Marques
Revista Portuguesa de Cardiologia (English Edition).2019; 38(9): 621. CrossRef - Increasing population size can inhibit cumulative cultural evolution
Nicolas Fay, Naomi De Kleine, Bradley Walker, Christine A. Caldwell
Proceedings of the National Academy of Sciences.2019; 116(14): 6726. CrossRef - Teachers’ perceptions of out-of-class communication, teacher-student relationship, and classroom environment
Amir Abd Elhay, Arnon Hershkovitz
Education and Information Technologies.2019; 24(1): 385. CrossRef - “You get what you appreciate”
Abderrahman Hassi
International Journal of Organizational Analysis.2019; 27(3): 786. CrossRef - Job crafting and customer service behaviors in the hospitality industry: Mediating effect of job passion
Hsiu-Yu Teng
International Journal of Hospitality Management.2019; 81: 34. CrossRef - Clinical outcomes of discordant exercise electrocardiographic and echocardiographic findings compared with concordant findings in patients with chest pain and no history of coronary artery disease
Hui-Jeong Hwang, Il Suk Sohn, Chang-Bum Park, Eun-Sun Jin, Jin-Man Cho, Chong-Jin Kim
Medicine.2019; 98(39): e17195. CrossRef - The Italian version of the Oral Health Impact Profile (OHIP-14) and its personality correlates
Lucia Monacis, Lorenzo Lo Muzio, Valeria de Palo, Guglielmo Campus, Livia Ottolenghi, Pietro Venezia, Maria Sinatra
PSICOLOGIA DELLA SALUTE.2019; (2): 123. CrossRef - Effects of a Translational Community-Based Multimodal Exercise Program on Quality of Life and the Influence of Start Delay on Physical Function and Quality of Life in Breast Cancer Survivors: A Pilot Study
Michael Paul Foley, Scott Michael Hasson, Eydie Kendall
Integrative Cancer Therapies.2018; 17(2): 337. CrossRef - A resilience safety climate model predicting construction safety performance
Yuting Chen, Brenda McCabe, Douglas Hyatt
Safety Science.2018; 109: 434. CrossRef - Comparison of Body Image Perception and Social Functioning Among Patients with End-Stage Renal Failure and Patients with Chronic Renal Failure
Nurgul Gungor Tavsanli, Sevgi Nehir
Iranian Red Crescent Medical Journal.2018;[Epub] CrossRef - Relationship Between Psychosocial Distress in Pregnancy and Two Genes Associated With Human Social Interaction: A Pilot Study
Sarah Dewell, Donna Slater, Karen Benzies, Sheila McDonald, Suzanne Tough
SAGE Open Nursing.2018;[Epub] CrossRef - Boat noise in an estuarine soundscape – A potential risk on the acoustic communication and reproduction of soniferous fish in the May River, South Carolina
Somers Smott, Agnieszka Monczak, Michaela E. Miller, Eric W. Montie
Marine Pollution Bulletin.2018; 133: 246. CrossRef - Polydrug use trajectories and differences in impulsivity among adolescents
Víctor Martínez-Loredo, José Ramón Fernández-Hermida, Alejandro de La Torre-Luque, Sergio Fernández-Artamendi
International Journal of Clinical and Health Psychology.2018; 18(3): 235. CrossRef - The Italian Version of the Cognitive Style Indicator and its Association with Decision-Making Preferences
Silvana Miceli, Valeria de Palo, Lucia Monacis, Maurizio Cardaci, Maria Sinatra
Creativity Research Journal.2018; 30(1): 85. CrossRef - Agricultural Education in Today’s School System: An Evaluation of Agricultural and Related Science Courses among High Schools in Alabama, USA
Rosny Jean, Colmore Christian
Social Sciences.2018; 7(11): 218. CrossRef - Multiculturality Concept and Its Reflections on Education: The Case of Turkey
Nilüfer KÖŞKER, Nurettin ÖZGEN
Review of International Geographical Education Online.2018; 8(3): 571. CrossRef - Quantitative trait locus analysis of seed germination, seedling vigour and seedling‐regulated hormones in Brassica napus
Tung C. T. Nguyen, Suzanne R. Abrams, Wolfgang Friedt, Rod J. Snowdon, Anne‐Marie Chevre
Plant Breeding.2018; 137(3): 388. CrossRef - Safety culture in the primary health care settings based on workers with a leadership role: the psychometric properties of the Slovenian-language version of the safety attitudes questionnaire – short form
Zalika Klemenc-Ketis, Irena Makivić, Antonija Poplas-Susič
BMC Health Services Research.2018;[Epub] CrossRef - Work–leisure conflict and its consequences: Do generational differences matter?
Sheng-Hshiung Tsaur, Chang-Hua Yen
Tourism Management.2018; 69: 121. CrossRef - Different cardiorespiratory fitness expressions based on the maximal cycle ergometer test show no effect on the relation of cardiorespiratory fitness to the academic achievement of nine-year-olds
Elvar Saevarsson, Erla Svansdottir, Sigurbjorn Arngrimsson, Thorarinn Sveinsson, Erlingur Johannsson, Luca Paolo Ardigò
PLOS ONE.2018; 13(7): e0200643. CrossRef - A Derivation of Factors Influencing the Innovation Diffusion of the OpenStreetMap in STEM Education
Steven J. H. Shiau, Chi-Yo Huang, Chia-Lee Yang, Jer-Nan Juang
Sustainability.2018; 10(10): 3447. CrossRef - Chemoradiation therapy induces in vivo changes in gene promoter methylation & gene transcript expression in patients with invasive cervical cancer
Swati Sood, Firuza D. Patel, Radhika Srinivasan, Lakhbir K. Dhaliwal
Indian Journal of Medical Research.2018; 147(2): 151. CrossRef - Authenticity and loyalty at heritage sites: The moderation effect of postmodern authenticity
Xiaoli Yi, Xiaoxiao Fu, Larry Yu, Liao Jiang
Tourism Management.2018; 67: 411. CrossRef - A multicenter examination and strategic revisions of the Yale Global Tic Severity Scale
Joseph F. McGuire, John Piacentini, Eric A. Storch, Tanya K. Murphy, Emily J. Ricketts, Douglas W. Woods, John W. Walkup, Alan L. Peterson, Sabine Wilhelm, Adam B. Lewin, James T. McCracken, James F. Leckman, Lawrence Scahill
Neurology.2018;[Epub] CrossRef - Estimation of body weight from the base of gait and the area swept in one stride—forensic implications
Bahadur Singh, Kewal Krishan, Kawaljit Kaur, Tanuj Kanchan
Egyptian Journal of Forensic Sciences.2018;[Epub] CrossRef - Farklı Aktivitelerin Yaşlıların Depresyon Seviyeleri Üzerine Etkileri
Orhan Koçak, Abdülhakim Beki, Serkan Eti
OPUS Uluslararası Toplum Araştırmaları Dergisi.2018;[Epub] CrossRef - CRMP2-binding compound, edonerpic maleate, accelerates motor function recovery from brain damage
Hiroki Abe, Susumu Jitsuki, Waki Nakajima, Yumi Murata, Aoi Jitsuki-Takahashi, Yuki Katsuno, Hirobumi Tada, Akane Sano, Kumiko Suyama, Nobuyuki Mochizuki, Takashi Komori, Hitoshi Masuyama, Tomohiro Okuda, Yoshio Goshima, Noriyuki Higo, Takuya Takahashi
Science.2018; 360(6384): 50. CrossRef - Robotic-assisted hysterectomy in a community hospital after seven years of experience
Zohreh Schuessler, Hans Schuessler, James Strohaber
Laparoscopic, Endoscopic and Robotic Surgery.2018; 1(2): 42. CrossRef - Shame and Defectiveness Beliefs in Treatment Seeking Patients With Body Dysmorphic Disorder
Hilary Weingarden, Ashley M. Shaw, Katharine A. Phillips, Sabine Wilhelm
Journal of Nervous & Mental Disease.2018; 206(6): 417. CrossRef - Localization accuracy of two electromagnetic tracking systems in prostate cancer radiotherapy: A comparison with fiducial marker based kilovoltage imaging
A. Vanhanen, H. Syrén, M. Kapanen
Physica Medica.2018; 56: 10. CrossRef - Phonological Awareness and Rapid Automatized Naming Are Independent Phonological Competencies With Specific Impacts on Word Reading and Spelling: An Intervention Study
Caroline Vander Stappen, Marie Van Reybroeck
Frontiers in Psychology.2018;[Epub] CrossRef - Exploring uses of the UK Clinical Aptitude Test‐situational judgement test in a dental student selection process
P. Lambe, E. Kay, D. Bristow
European Journal of Dental Education.2018; 22(1): 23. CrossRef - Applicability of the Ben-Tovim Walker Body Attitude Questionnaire in Moslem women
Zahra Toghiyani, Ashraf Kazemi, Nafisehsadat Nekuei, Mousa Alavi, Marjan Beigi
Psychology, Health & Medicine.2018; 23(6): 717. CrossRef - Fear of Missing Out as a Predictor of Problematic Social Media Use and Phubbing Behavior among Flemish Adolescents
Vittoria Franchina, Mariek Vanden Abeele, Antonius J. Van Rooij, Gianluca Lo Coco, Lieven De Marez
International Journal of Environmental Research and Public Health.2018; 15(10): 2319. CrossRef - Young drivers and their cars: Safe and sound or the perfect storm?
Oscar Oviedo-Trespalacios, Bridie Scott-Parker
Accident Analysis & Prevention.2018; 110: 18. CrossRef - Towards a reliable repeated-measures beads task for assessing the jumping to conclusions bias
Benjamin F. McLean, Julie K. Mattiske, Ryan P. Balzan
Psychiatry Research.2018; 265: 200. CrossRef - Further development and testing of the metacognitive model of procrastination: Self-reported academic performance
Bruce A. Fernie, Umran Y. Kopar, Peter L. Fisher, Marcantonio M. Spada
Journal of Affective Disorders.2018; 240: 1. CrossRef - Preliminary Data Validation and Reconstruction of Temperature and Precipitation in Central Italy
Matteo Gentilucci, Maurizio Barbieri, Peter Burt, Fabrizio D’Aprile
Geosciences.2018; 8(6): 202. CrossRef - Non-Dependent and Dependent Daily Cannabis Users Differ in Mental Health but Not Prospective Memory Ability
Ruth Braidwood, Samantha Mansell, Jon Waldron, Peter G. Rendell, Sunjeev K. Kamboj, H. Valerie Curran
Frontiers in Psychiatry.2018;[Epub] CrossRef - Blind wayfinding with physically-based liquid sounds
Simone Spagnol, Rebekka Hoffmann, Marcelo Herrera Martínez, Runar Unnthorsson
International Journal of Human-Computer Studies.2018; 115: 9. CrossRef - Anxiety moderates the effects of stressor controllability and cognitive reappraisal on distress following aversive exposure: An experimental investigation
Lillian Le, Michelle Moulds, Angela Nickerson
Journal of Behavior Therapy and Experimental Psychiatry.2018; 60: 87. CrossRef - An Exploration of the Factor Structure of Executive Functioning in Children
David Messer, Marialivia Bernardi, Nicola Botting, Elisabeth L. Hill, Gilly Nash, Hayley C. Leonard, Lucy A. Henry
Frontiers in Psychology.2018;[Epub] CrossRef - Constructing a model of exhibition attachment: Motivation, attachment, and loyalty
Xiaoli Yi, Xiaoxiao Fu, Wenmin Jin, Fevzi Okumus
Tourism Management.2018; 65: 224. CrossRef - Influence of celebrity involvement on place attachment: role of destination image in film tourism
Chien-Yu Chen
Asia Pacific Journal of Tourism Research.2018; 23(1): 1. CrossRef - Impaired Efficiency and Resilience of Structural Network in Spinocerebellar Ataxia Type 3
Yu-Te Wu, Shang-Ran Huang, Chi-Wen Jao, Bing-Wen Soong, Jiing-Feng Lirng, Hsiu-Mei Wu, Po-Shan Wang
Frontiers in Neuroscience.2018;[Epub] CrossRef - Designing Awe in Virtual Reality: An Experimental Study
Alice Chirico, Francesco Ferrise, Lorenzo Cordella, Andrea Gaggioli
Frontiers in Psychology.2018;[Epub] CrossRef - Parental Self-Efficacy to Support Teens During a Suicidal Crisis and Future Adolescent Emergency Department Visits and Suicide Attempts
Ewa K. Czyz, Adam G. Horwitz, Carlos E. Yeguez, Cynthia J. Ewell Foster, Cheryl A. King
Journal of Clinical Child & Adolescent Psychology.2018; 47(sup1): S384. CrossRef - How is negative affect associated with life satisfaction? The moderating role of online self-disclosure in China's context
Ge Wang, Wei Zhang, Qiang Chen, Runxi Zeng
Personality and Individual Differences.2018; 135: 60. CrossRef - Motor abilities and relative age effect of adolescents
Igor Vučković, Aleksandar Kukrić, Aleksandar Gadžić, Borko Petrović, Saša Marković, Nemanja Zlojutro
Fizicka kultura.2018; 72(2): 181. CrossRef - Can proxy assessments serve as a first screener for identifying people at risk for multidimensional frailty?
Anne van der Vorst, G. A. Rixt Zijlstra, Nico De Witte, Jan De Lepeleire, Gertrudis I. J. M. Kempen, Jos M. G. A. Schols
European Geriatric Medicine.2018; 9(4): 501. CrossRef - Does Repeated Testing Impact Concordance Between Genital and Self-Reported Sexual Arousal in Women?
Julia Velten, Meredith L. Chivers, Lori A. Brotto
Archives of Sexual Behavior.2018; 47(3): 651. CrossRef - The influence of impulsivity and the Dark Triad on self-reported aggressive driving behaviours
Laura Ball, Ruth Tully, Vincent Egan
Accident Analysis & Prevention.2018; 120: 130. CrossRef - Effect of multi-micronutrient-fortified rice on cognitive performance depends on premix composition and cognitive function tested: results of an effectiveness study in Cambodian schoolchildren
Marion Fiorentino, Marlène Perignon, Khuov Kuong, Richard de Groot, Megan Parker, Kurt Burja, Marjoleine A Dijkhuizen, Sek Sokhom, Chhoun Chamnan, Jacques Berger, Frank T Wieringa
Public Health Nutrition.2018; 21(4): 816. CrossRef - Relationship between working memory and comprehension and expression of grammar in Farsi-speaking children with cochlear implants
Soodeh Khoramian, Zahra Soleymani
International Journal of Pediatric Otorhinolaryngology.2018; 113: 240. CrossRef - Consumers' Stickiness to Mobile Payment Applications
Elizabeth D. Matemba, Guoxin Li, Baraka J. Maiseli
Journal of Database Management.2018; 29(3): 43. CrossRef - Statistical Similarities Between WSA‐ENLIL+Cone Model and MAVEN in Situ Observations From November 2014 to March 2016
C. L. Lentz, D. N. Baker, A. N. Jaynes, R. M. Dewey, C. O. Lee, J. S. Halekas, D. A. Brain
Space Weather.2018; 16(2): 157. CrossRef - Depression symptoms and reasons for gambling sequentially mediate the associations between insecure attachment styles and problem gambling
Matthew T. Keough, Trinda L. Penniston, Natalie Vilhena-Churchill, R. Michael Bagby, Lena C. Quilty
Addictive Behaviors.2018; 78: 166. CrossRef - Short version of the Smartphone Addiction Scale in Chinese adults: Psychometric properties, sociodemographic, and health behavioral correlates
Tzu Tsun Luk, Man Ping Wang, Chen Shen, Alice Wan, Pui Hing Chau, John Oliffe, Kasisomayajula Viswanath, Sophia Siu-chee Chan, Tai Hing Lam
Journal of Behavioral Addictions.2018; 7(4): 1157. CrossRef - Rash Impulsiveness and Negative Mood, but not Alexithymia or Reward Sensitivity, Differentiate Young to Middle-Aged Chronic Daily Smokers from Never-Smokers
Michael Lyvers, Monique Bremner, Mark S. Edwards, Fred Arne Thorberg
Journal of Psychoactive Drugs.2018; 50(1): 33. CrossRef - Self-esteem in adults with Tourette syndrome and chronic tic disorders: The roles of tic severity, treatment, and comorbidity
Hilary Weingarden, Lawrence Scahill, Susanne Hoeppner, Alan L. Peterson, Douglas W. Woods, John T. Walkup, John Piacentini, Sabine Wilhelm
Comprehensive Psychiatry.2018; 84: 95. CrossRef - Assessing Households’ Gas and Electricity Consumption: A Case Study of Djelfa, Algeria
Soufiane Boukarta, Ewa Berezowska-Azzag
Quaestiones Geographicae.2018; 37(4): 111. CrossRef - Parameter variations within Li-Ion battery packs – Theoretical investigations and experimental quantification
Michael Baumann, Leo Wildfeuer, Stephan Rohr, Markus Lienkamp
Journal of Energy Storage.2018; 18: 295. CrossRef - Social Support Moderates Effects of Natural Disaster Exposure on Depression and Posttraumatic Stress Disorder Symptoms: Effects for Displaced and Nondisplaced Residents
Adam P. McGuire, Jami M. Gauthier, Lisa M. Anderson, David W. Hollingsworth, Melissa Tracy, Sandro Galea, Scott F. Coffey
Journal of Traumatic Stress.2018; 31(2): 223. CrossRef - University employees' preparedness for natural hazards and incidents of mass violence: An application of the extended parallel process model
Marcela C. Weber, Stefan E. Schulenberg, Elicia C. Lair
International Journal of Disaster Risk Reduction.2018; 31: 1082. CrossRef - Social network plasticity decreases disease transmission in a eusocial insect
Nathalie Stroeymeyt, Anna V. Grasse, Alessandro Crespi, Danielle P. Mersch, Sylvia Cremer, Laurent Keller
Science.2018; 362(6417): 941. CrossRef - Investigating the mediational role of negative urgency in the anxiety sensitivity pathway to cannabis problems and dependence symptoms among postsecondary students
Matthew T. Keough, Christian S. Hendershot, Jeffrey D. Wardell, R. Michael Bagby
Journal of American College Health.2018; 66(2): 69. CrossRef - Interactive effects of early life stress and CACNA1C genotype on cortisol awakening response
K. Klaus, K. Butler, H. Gutierrez, S.J. Durrant, K. Pennington
Biological Psychology.2018; 136: 22. CrossRef - Characteristic Analysis of Pressure Fluctuation and Free Surface Displacement in River-Crossing Structure through Statistical Approach
Hyungju Yoo, Seoungoh Lee, Moonhyung Park
Journal of the Korean Society of Hazard Mitigation.2018; 18(6): 385. CrossRef - A Functional Polymorphism in the DRD1 Gene, That Modulates Its Regulation by miR-504, Is Associated with Depressive Symptoms
Karen M. Jiménez, Angela J. Pereira-Morales, Diego A. Forero
Psychiatry Investigation.2018; 15(4): 402. CrossRef - MTHFR gene methylation is associated with perceived stress in healthy young adults
Karen M. Jiménez, Angela J. Pereira-Morales, Diego A. Forero
Psychiatric Genetics.2018; 28(3): 41. CrossRef - Do personality traits and self‐regulatory processes affect decision‐making tendencies?
Silvana Miceli, Valeria De palo, Lucia Monacis, Santo Di nuovo, Maria Sinatra
Australian Journal of Psychology.2018; 70(3): 284. CrossRef - Quantitative mapping and predictive modeling of Mn nodules' distribution from hydroacoustic and optical AUV data linked by random forests machine learning
Iason-Zois Gazis, Timm Schoening, Evangelos Alevizos, Jens Greinert
Biogeosciences.2018; 15(23): 7347. CrossRef - Разработка методики самоактивации личности
Мария Одинцова, Наталия Радчикова
Психологические исследования.2018;[Epub] CrossRef - Natural variation in GmGBP1 promoter affects photoperiod control of flowering time and maturity in soybean
Lin Zhao, Minmin Li, Chongjing Xu, Xue Yang, Dongmei Li, Xue Zhao, Kuo Wang, Yinghua Li, Xiaoming Zhang, Lixue Liu, Fuquan Ding, Hailong Du, Chunsheng Wang, Jingzhe Sun, Wenbin Li
The Plant Journal.2018; 96(1): 147. CrossRef - Temporal and Spatial Flow Variations over a Movable Scour Hole Downstream of a Grade-Control Structure with a PIV System
Shi-Yan Lu, Jau-Yau Lu, Dong-Sin Shih
Water.2018; 10(8): 1002. CrossRef - Share price reaction to financial and integrated reports
Gizelle D. Willows, Jessica A. Rockey
South African Journal of Accounting Research.2018; 32(2-3): 174. CrossRef - Korean consumers’ acceptability of commercial food products and usage of the 9‐point hedonic scale
Jiyun Yang, Jeehyun Lee
Journal of Sensory Studies.2018;[Epub] CrossRef - Assessment of the Italian Version of the Internet Disorder Scale (IDS-15)
Lucia Monacis, Maria Sinatra, Mark D. Griffiths, Valeria de Palo
International Journal of Mental Health and Addiction.2018; 16(3): 680. CrossRef - Validating the Material Values Scale for Children (MVS-c) for Use in Early Childhood
Heleen van der Meulen, Rinaldo Kühne, Suzanna J. Opree
Child Indicators Research.2018; 11(4): 1201. CrossRef - Change in Activities of Daily Living in the Year Following a Stroke
Hsiang-Chu Pai, Mei-Yu Lai, An-Chih Chen, Pei-Shan Lin
Nursing Research.2018; 67(4): 286. CrossRef - Anxiety symptomatology, sex and chronotype: The mediational effect of diurnal sleepiness
Angela J. Pereira-Morales, Ana Adan, Ivana L. Bussi, Andrés Camargo
Chronobiology International.2018; 35(10): 1354. CrossRef - Determinants of research collaboration towards a knowledge-based economy in Ghana
Mavis S. B. Mensah, Francis Enu-Kwesi
Industry and Higher Education.2018; 32(5): 326. CrossRef - Situation Awareness Performance in Healthy Young Adults Is Associated With a Serotonin Transporter Gene Polymorphism
Yeimy González-Giraldo, Rodrigo E. González-Reyes, Shane T. Mueller, Brian J. Piper, Ana Adan, Diego A. Forero
Psychological Reports.2018; 121(5): 877. CrossRef - Are Women’s Orgasms Hindered by Phallocentric Imperatives?
Malachi Willis, Kristen N. Jozkowski, Wen-Juo Lo, Stephanie A. Sanders
Archives of Sexual Behavior.2018; 47(6): 1565. CrossRef - Personality traits and health-related quality of life: the mediator role of coping strategies and psychological distress
Angela J. Pereira-Morales, Ana Adan, Sandra Lopez-Leon, Diego A. Forero
Annals of General Psychiatry.2018;[Epub] CrossRef - Exploring relationships among social integration, social isolation, self-rated health, and demographics among Latino day laborers
Kenneth C. Steel, Maria Eugenia Fernandez-Esquer, John S. Atkinson, Wendell C. Taylor
Ethnicity & Health.2018; 23(4): 425. CrossRef - ANN and Fuzzy Logic Based Model to Evaluate Huntington Disease Symptoms
Andrius Lauraitis, Rytis Maskeliūnas, Robertas Damaševičius
Journal of Healthcare Engineering.2018; 2018: 1. CrossRef - Destiansyon Çelim Unsurlarının Ziyaretçi Tatmini Üzerine Etkisi: Kırklareli İli Örneği
İlke Başarangil
Pamukkale University Journal of Social Sciences Institute.2018;[Epub] CrossRef - Improvements in fitness are not obligatory for exercise training-induced improvements in CV risk factors
Yvonne A. W. Hartman, Maria T. E. Hopman, Tim H. Schreuder, Rebecca J. H. M. Verheggen, Ralph R. Scholten, Madelijn H. Oudegeest-Sander, Fleur Poelkens, Andrew J. Maiorana, Louise H. Naylor, Peter H. Willems, Cees J. Tack, Dick H. J. Thijssen, Daniel J. G
Physiological Reports.2018; 6(4): e13595. CrossRef - Identifying the unique role of orthographic working memory in a componential model of Hong Kong kindergarteners’ Chinese written spelling
Jianhong Mo, Catherine McBride, Laiying Yip
Reading and Writing.2018; 31(5): 1083. CrossRef - The Function of Personality in Suicidal Ideation from the Perspective of the Interpersonal-Psychological Theory of Suicide
Marc Baertschi, Alessandra Costanza, Alessandra Canuto, Kerstin Weber
International Journal of Environmental Research and Public Health.2018; 15(4): 636. CrossRef - Extraversion and happiness: The mediating role of social support and hope
Chee‐Seng Tan, Sew‐Kim Low, Glory Nancy Viapude
PsyCh Journal.2018; 7(3): 133. CrossRef - The Effects of Out-of-School Learning Settings Science Activities on 5th Graders’ Academic Achievement
Busra Bakioglu, Orhan Karamustafaoglu, Sevilay Karamustafaoglu, Senay Yapici
European Journal of Educational Research.2018; volume-7-2(volume7-is): 451. CrossRef - Mental distress and perceived wealth, justice and freedom across eight countries: The invisible power of the macrosystem
Saskia Scholten, Julia Velten, Jürgen Margraf, Monica Uddin
PLOS ONE.2018; 13(5): e0194642. CrossRef - An exploration of the link between adult attachment and problematic Facebook use
Sally Flynn, Chris Noone, Kiran M. Sarma
BMC Psychology.2018;[Epub] CrossRef - A brief cognitive therapy intervention for internalised stigma in acute inpatients who experience psychosis: A feasibility randomised controlled trial
Lisa Wood, Rory Byrne, Gabriela Enache, Anthony P. Morrison
Psychiatry Research.2018; 262: 303. CrossRef - Family Influence, Critical Consciousness, and Career Calling in Women of Color
Laura Reid Marks, Leigh M. Harrell‐Williams, Kevin A. Tate, Monica L. Coleman, Kanesha Moore
The Career Development Quarterly.2018; 66(4): 329. CrossRef - Job resourcefulness, work engagement and prosocial service behaviors in the hospitality industry
Jui-Chang Cheng, Chien-Yu Chen
International Journal of Contemporary Hospitality Management.2017; 29(10): 2668. CrossRef - Avaliação da normalidade dos dados em estudos clínicos e experimentais
Hélio Amante Miot
Jornal Vascular Brasileiro.2017; 16(2): 88. CrossRef - An open-label randomised controlled trial on the efficacy of adding intranasal fentanyl to intravenous tramadol in patients with moderate to severe pain following acute musculoskeletal injuries
KS Chew, AH Shaharudin
Singapore Medical Journal.2017; 58(10): 601. CrossRef - The Longitudinal Contribution of Early Morphological Awareness Skills to Reading Fluency and Comprehension in Greek
George Manolitsis, Ioannis Grigorakis, George K. Georgiou
Frontiers in Psychology.2017;[Epub] CrossRef - Propiedades psicométricas de un Stroop emocional computarizado para evaluar vulnerabilidad cognitiva
Ronald Alberto Toro Tobar, Bertha Lucía Avendaño Prieto, Hugo Alejandro Arias López, Julián Camilo Sarmiento-López
Revista CES Psicología.2017; 10(2): 103. CrossRef - Work stress, anthropometry, lung function, blood pressure, and blood-based biomarkers: a cross-sectional study of 43,593 French men and women
Linda L. Magnusson Hanson, Hugo Westerlund, Marcel Goldberg, Marie Zins, Jussi Vahtera, Naja Hulvej Rod, Sari Stenholm, Andrew Steptoe, Mika Kivimäki
Scientific Reports.2017;[Epub] CrossRef - Long-term acoustic monitoring of fish calling provides baseline estimates of reproductive timelines in the May River estuary, southeastern USA
A Monczak, A Berry, C Kehrer, EW Montie
Marine Ecology Progress Series.2017; 581: 1. CrossRef - Topiramate and accommodation: Does topiramate cause accommodative dysfunction?
Eren Çerman, Semra Akkaya Turhan, Muhsin Eraslan, Pınar Kahraman Koytak, Özden Kilinç, Tülin Tanrıdağ
Canadian Journal of Ophthalmology.2017; 52(1): 20. CrossRef - Procrastination is Detrimental to Undergraduate Students’ Self-Rated Creativity: The Mediating Role of State Anxiety
Jia-Wei Lim, Joo-Yee Phang, Mei-Yan Low, Chee-Seng Tan
Creativity. Theories – Research - Applications.2017; 4(1): 99. CrossRef - Social networking addiction, attachment style, and validation of the Italian version of the Bergen Social Media Addiction Scale
Lucia Monacis, Valeria de Palo, Mark D. Griffiths, Maria Sinatra
Journal of Behavioral Addictions.2017; 6(2): 178. CrossRef - DLLs and the development of self-regulation in early childhood
Ruth Guirguis, Kathy Carolina Antigua, John Lee
Cogent Education.2017; 4(1): 1355628. CrossRef - Predicting the integrated development of word reading and spelling in the early primary grades
Moniek M.H. Schaars, Eliane Segers, Ludo Verhoeven
Learning and Individual Differences.2017; 59: 127. CrossRef - Stress-induced change in serum BDNF is related to quantitative family history of alcohol use disorder and age at first alcohol use
Shobhit Sharma, Reiko Graham, Rodney Rohde, Natalie A. Ceballos
Pharmacology Biochemistry and Behavior.2017; 153: 12. CrossRef - Preliminary validation of the Portuguese Edinburgh Handedness Inventory in an adult sample
Helena Espírito-Santo, Catarina Freitas Pires, Inês Queiroz Garcia, Fernanda Daniel, Alexandre Gomes da Silva, Rachel L. Fazio
Applied Neuropsychology: Adult.2017; 24(3): 275. CrossRef - Long‐term reliability and stability of behavioral measures among adolescents: The Delay Discounting and Stroop tasks
Víctor Martínez‐Loredo, José Ramón Fernández‐Hermida, José Luis Carballo, Sergio Fernández‐Artamendi
Journal of Adolescence.2017; 58(1): 33. CrossRef - Health Expenditure and All-Cause Mortality in the ‘Galaxy’ of Italian Regional Healthcare Systems: A 15-Year Panel Data Analysis
Davide Golinelli, Fabrizio Toscano, Andrea Bucci, Jacopo Lenzi, Maria Pia Fantini, Nicola Nante, Gabriele Messina
Applied Health Economics and Health Policy.2017; 15(6): 773. CrossRef - On the stochastic variations of intra-tow permeability induced by internal geometry variability in a 2/2 twill carbon fabric
M. Bodaghi, A. Vanaerschot, S. V. Lomov, N. C. Correia
Composites Part A: Applied Science and Manufacturing.2017; 101: 444. CrossRef - Sterile corneal infiltrates after corneal collagen cross‐linking: evaluation of risk factors
Eren Çerman, Deniz Özarslan Özcan, Ebru Toker
Acta Ophthalmologica.2017; 95(2): 199. CrossRef - An industry experiment on the effects of test-driven development on external quality and productivity
Ayse Tosun, Oscar Dieste, Davide Fucci, Sira Vegas, Burak Turhan, Hakan Erdogmus, Adrian Santos, Markku Oivo, Kimmo Toro, Janne Jarvinen, Natalia Juristo
Empirical Software Engineering.2017; 22(6): 2763. CrossRef - A smartphone “app”-delivered randomized factorial trial targeting physical activity in adults
Jason Fanning, Sarah Roberts, Charles H. Hillman, Sean P. Mullen, Lee Ritterband, Edward McAuley
Journal of Behavioral Medicine.2017; 40(5): 712. CrossRef - ‘Join The Walk?’: Short-term and follow-up effects of a 10-week walking intervention in patients with a mental disorder
Jari Vanroy, Jan Seghers, An Bogaerts, Anne Wijtzes, Filip Boen
Mental Health and Physical Activity.2017; 12: 73. CrossRef - Application of Enhanced Point Estimators to a Sample of In Vivo CT‐derived Facial Soft Tissue Thicknesses
Connie L. Parks, Kelsey M. Kyllonen, Keith L. Monson
Journal of Forensic Sciences.2017; 62(4): 994. CrossRef - Transfer from implicit to explicit phonological abilities in first and second language learners
CARESSA JANSSEN, ELIANE SEGERS, JAMES M. MCQUEEN, LUDO VERHOEVEN
Bilingualism: Language and Cognition.2017; 20(4): 795. CrossRef - Val158Met polymorphism in the COMT gene is associated with hypersomnia and mental health-related quality of life in a Colombian sample
Karen M. Jiménez, Angela J. Pereira-Morales, Diego A. Forero
Neuroscience Letters.2017; 644: 43. CrossRef - Surveying prenatal attachment in fathers: the Italian adaptation of the Paternal Antenatal Attachment Scale (PAAS-IT)
Anna M. Della Vedova, Roberto Burro
Journal of Reproductive and Infant Psychology.2017; 35(5): 493. CrossRef - The Role of Self-Esteem and Social Support in the Relationship between Extraversion and Happiness: a Serial Mediation Model
Chee-Seng Tan, Sanggari A/P Krishnan, Qi-Wen Lee
Current Psychology.2017; 36(3): 556. CrossRef - Higher scores in the extraversion personality trait are associated with a functional polymorphism in thePER3gene in healthy subjects
Karen M. Jiménez, Angela J. Pereira-Morales, Diego A. Forero
Chronobiology International.2017; 34(2): 280. CrossRef - Building customer satisfaction with tour leaders: the roles of customer trust, justice perception, and cooperation in group package tours
Jui-Chang Cheng, Chien-Yu Chen, Chang-Hua Yen, Hsiu-Yu Teng
Asia Pacific Journal of Tourism Research.2017; 22(4): 395. CrossRef - Relationship between Individual Resilience, Interpersonal Conflicts at Work, and Safety Outcomes of Construction Workers
Yuting Chen, Brenda McCabe, Douglas Hyatt
Journal of Construction Engineering and Management.2017;[Epub] CrossRef - Retention of Antibacterial Activity in Geranium Plasma Polymer Thin Films
Ahmed Al-Jumaili, Kateryna Bazaka, Mohan Jacob
Nanomaterials.2017; 7(9): 270. CrossRef - Directional and Causal Information Flow in EEG for Assessing Perceived Audio Quality
Ketan Mehta, Jorg Kliewer
IEEE Transactions on Molecular, Biological and Multi-Scale Communications.2017; 3(3): 150. CrossRef - COMPARISON OF FEMALE AND MALE YOUTH CHARACTERISTICS PRIOR TO ENTREPRENEURIAL DEVELOPMENT: EVIDENCE FROM UGANDA
FREDDIE FESTO MAWANGA
Journal of Developmental Entrepreneurship.2017; 22(01): 1750004. CrossRef - Subjectivity of teacher judgments: Exploring student characteristics that influence teacher judgments of student ability
Kane Meissel, Frauke Meyer, Esther S. Yao, Christine M. Rubie-Davies
Teaching and Teacher Education.2017; 65: 48. CrossRef - Fun Seeking and Reward Responsiveness Moderate the Effect of the Behavioural Inhibition System on Coping-Motivated Problem Gambling
Matthew T. Keough, Jeffrey D. Wardell, Christian S. Hendershot, R. Michael Bagby, Lena C. Quilty
Journal of Gambling Studies.2017; 33(3): 769. CrossRef - Construction Equipment Management Practices for Improving Labor Productivity in Multistory Building Construction Projects
Argaw Tarekegn Gurmu, Ajibade Ayodeji Aibinu
Journal of Construction Engineering and Management.2017;[Epub] CrossRef - Organized leisure-time sport participation and academic achievement in preadolescents
Elvar Smari Sævarsson, Erla Svansdottir, Thorarinn Sveinsson, Tinna Laufey Asgeirsdottir, Sigurbjorn Arni Arngrimsson, Erlingur Johannsson
Scandinavian Journal of Public Health.2017; 45(8): 861. CrossRef - The flashlights on a distinct role of protein kinase C δ: Phosphorylation of regulatory and catalytic domain upon oxidative stress in glioma cells
Matus Misuth, Jaroslava Joniova, Denis Horvath, Lenka Dzurova, Zuzana Nichtova, Marta Novotova, Pavol Miskovsky, Katarina Stroffekova, Veronika Huntosova
Cellular Signalling.2017; 34: 11. CrossRef - From words to text: inference making mediates the role of vocabulary in children’s reading comprehension
Hanne Trebbien Daugaard, Kate Cain, Carsten Elbro
Reading and Writing.2017; 30(8): 1773. CrossRef - The emotion regulation questionnaire in women with cancer: A psychometric evaluation and an item response theory analysis
Tânia Brandão, Marc S. Schulz, James J. Gross, Paula Mena Matos
Psycho-Oncology.2017; 26(10): 1647. CrossRef - Impact of individual resilience and safety climate on safety performance and psychological stress of construction workers: A case study of the Ontario construction industry
Yuting Chen, Brenda McCabe, Douglas Hyatt
Journal of Safety Research.2017; 61: 167. CrossRef - Effects of behavioural activation on the neural basis of other perspective self-referential processing in subthreshold depression: a functional magnetic resonance imaging study
S. Shiota, Y. Okamoto, G. Okada, K. Takagaki, M. Takamura, A. Mori, S. Yokoyama, Y. Nishiyama, R. Jinnin, R. I. Hashimoto, S. Yamawaki
Psychological Medicine.2017; 47(5): 877. CrossRef - Importance Level of Construction Managers’ Technical Competency Across Different Contractors’ Demographics in Malaysia
Hairuddin Mohammad, Padzil Fadzil Hassan, Siti Khalijah Yaman, M.J. Zainorizuan, L. Yee Yong, L. Alvin John Meng Siang, O. Mohamad Hanifi, R. Siti Nazahiyah, A. Mohd Shalahuddin
MATEC Web of Conferences.2017; 103: 03012. CrossRef - Elevated cortisol awakening response associated with early life stress and impaired executive function in healthy adult males
Kevin Butler, Kristel Klaus, Laura Edwards, Kyla Pennington
Hormones and Behavior.2017; 95: 13. CrossRef - Validation of the Internet Gaming Disorder Scale – Short-Form (IGDS9-SF) in an Italian-speaking sample
Lucia Monacis, Valeria de Palo, Mark D. Griffiths, Maria Sinatra
Journal of Behavioral Addictions.2016; 5(4): 683. CrossRef - Source Wavelet Phase Extraction
Diako Hariri Naghadeh, Christopher Keith Morley
Pure and Applied Geophysics.2016; 173(6): 2011. CrossRef - “Does global sourcing pay-off? A competitive dynamics perspective”
Frederik G.S. Vos, Paul Scheffler, Holger Schiele, Philipp Horn
Journal of Purchasing and Supply Management.2016; 22(4): 338. CrossRef - Heterogeneity of non-cancerous liver parenchyma on gadoxetic acid-enhanced MRI: an imaging biomarker for hepatocellular carcinoma development in chronic liver disease
Y. Asayama, A. Nishie, K. Ishigami, Y. Ushijima, Y. Takayama, D. Okamoto, N. Fujita, K. Morita, M. Obara, H. Honda
Clinical Radiology.2016; 71(5): 432. CrossRef - Type and Quantity of Shipborne Garbage at Selected Tropical Beaches
Julyus-Melvin Mobilik, Teck-Yee Ling, Mohd-Lokman Husain, Ruhana Hassan
The Scientific World Journal.2016; 2016: 1. CrossRef - Memória e envelhecimento: Qual o real impacto da idade?
Helena Espirito-Santo, Inês Torres Pena, Inês Queiroz Garcia, Catarina Freitas Pires, Margarida Couto, Fernanda Daniel
Revista Portuguesa de Investigação Comportamental e Social.2016; 2(2): 41. CrossRef - Propriedades psicométricas da versão Torga do Teste Stroop
Inês Queiroz Garcia, Inês Amaral Pessoa, Bárbara Monteiro, Fernanda Daniel, Laura Lemos, Helena Espirito Santo
Revista Portuguesa de Investigação Comportamental e Social.2016; 2(2): 55. CrossRef - Physical and functional outcomes following multidisciplinary residential rehabilitation for prearthritic hip pain among young active UK military personnel
Russell J Coppack, James L Bilzon, Andrew K Wills, Ian M McCurdie, Laura K Partridge, Alastair M Nicol, Alexander N Bennett
BMJ Open Sport & Exercise Medicine.2016; 2(1): e000107. CrossRef - Avaliação breve do défice executivo em pessoas idosas com Acidente Vascular Cerebral: Validação da Bateria de Avaliação Frontal
Helena Espirito-Santo, Inês Queiroz Garcia, Bárbara Monteiro, Naír Carolino, Fernanda Daniel
Revista Portuguesa de Investigação Comportamental e Social.2016; 2(2): 25. CrossRef - DNMT1 Regulates Epithelial-Mesenchymal Transition and Cancer Stem Cells, Which Promotes Prostate Cancer Metastasis
Eunsohl Lee, Jingcheng Wang, Kenji Yumoto, Younghun Jung, Frank C. Cackowski, Ann M. Decker, Yan Li, Renny T. Franceschi, Kenneth J. Pienta, Russell S. Taichman
Neoplasia.2016; 18(9): 553. CrossRef - Modeling Age-Friendly Environment, Active Aging, and Social Connectedness in an Emerging Asian Economy
Ming-Ming Lai, Shi-Ying Lein, Siok-Hwa Lau, Ming-Ling Lai
Journal of Aging Research.2016; 2016: 1. CrossRef - Psychometric study of the European Portuguese version of the PedsQL 3.0 Cancer Module
Susana Santos, Carla Crespo, M. Cristina Canavarro, Ananda Fernandes, Luís Batalha, Diana de Campos, Armando Pinto
Health and Quality of Life Outcomes.2016;[Epub] CrossRef - Exploration of the Effectiveness and Acceptability of a Professional Mindfulness Retreat for Psychiatrists
Russell Razzaque, Lisa Wood
Mindfulness.2016; 7(2): 340. CrossRef - Main concepts for three different discourse tasks in a large non-clinical sample
Jessica D. Richardson, Sarah Grace Dalton
Aphasiology.2016; 30(1): 45. CrossRef - Movement of three stream‐resident balitoroid loaches and a goby in a Hong Kong hillstream
Bill S.K. Ho, David Dudgeon
Ecology of Freshwater Fish.2016; 25(4): 622. CrossRef - Dermal Structure in Lymphedema Patients with History of Acute Dermatolymphangioadenitis Evaluated by Histogram Analysis of Ultrasonography Findings: A Case-Control Study
Misako Dai, Aya Sato, Hiroko Maeba, Terumi Iuchi, Masaru Matsumoto, Mayumi Okuwa, Toshio Nakatani, Hiromi Sanada, Junko Sugama
Lymphatic Research and Biology.2016; 14(1): 2. CrossRef - “Put the blame on…others!”: The battle of cyclists against pedestrians and car drivers at the urban environment. A cyclists’ perception study
Evangelos Paschalidis, Socrates Basbas, Ioannis Politis, Mixalis Prodromou
Transportation Research Part F: Traffic Psychology and Behaviour.2016; 41: 243. CrossRef - A Gaussian Model-Based Probabilistic Approach for Pulse Transit Time Estimation
Dae-Geun Jang, Seung-Hun Park, Minsoo Hahn
IEEE Journal of Biomedical and Health Informatics.2016; 20(1): 128. CrossRef - Histogram analysis of noncancerous liver parenchyma on gadoxetic acid-enhanced MRI: predictive value for liver function and pathology
Yoshiki Asayama, Akihiro Nishie, Kousei Ishigami, Yasuhiro Ushijima, Yukihisa Takayama, Daisuke Okamoto, Nobuhiro Fujita, Tomoharu Yoshizumi, Tomoyuki Hida, Hiroshi Honda
Abdominal Radiology.2016; 41(9): 1751. CrossRef - Disentangling the influence of earthworms in sugarcane rhizosphere
Lucas P. P. Braga, Caio A. Yoshiura, Clovis D. Borges, Marcus A. Horn, George G. Brown, Harold L. Drake, Siu M. Tsai
Scientific Reports.2016;[Epub] CrossRef - The effects of aerobic exercise on cognition in schizophrenia: A 3-month follow-up study
Chwen-Yng Su, Peng-Wei Wang, Yi-Jean Lin, Tze-Chun Tang, Mei-Fang Liu, Ming-De Chen
Psychiatry Research.2016; 244: 394. CrossRef - The Applicability of Wildlife Value Orientations Scales to a Muslim Student Sample in Malaysia
Zulkhairi Azizi Zainal Abidin, Maarten H. Jacobs
Human Dimensions of Wildlife.2016; 21(6): 555. CrossRef - Co‐ingestion of energy drinks with alcohol and other substances among a sample of people who regularly use ecstasy
Amy Peacock, Natasha Sindicich, Matthew Dunn, Elizabeth Whittaker, Rachel Sutherland, Gavin Entwistle, Lucinda Burns, Raimondo Bruno
Drug and Alcohol Review.2016; 35(3): 352. CrossRef -
Validating the Use of
D
for Measuring Lexical Diversity in Low-Income Kindergarten Children
Stephanie A. Lai, Paula J. Schwanenflugel
Language, Speech, and Hearing Services in Schools.2016; 47(3): 225. CrossRef - Sleep quality, chronotype and social jetlag differentially associate with symptoms of attention deficit hyperactivity disorder in adults
Niall M. McGowan, Bogdan I. Voinescu, Andrew N. Coogan
Chronobiology International.2016; 33(10): 1433. CrossRef - Can professional development of teachers reduce disparity in student achievement?
Kane Meissel, Judy M. Parr, Helen S. Timperley
Teaching and Teacher Education.2016; 58: 163. CrossRef - In search of patterns among travellers' hotel ratings in TripAdvisor
Snehasish Banerjee, Alton Y.K. Chua
Tourism Management.2016; 53: 125. CrossRef - The functional and clinical outcomes of exercise training following a very low energy diet for severely obese women: study protocol for a randomised controlled trial
Clint T. Miller, Steve F. Fraser, Steve E. Selig, Toni Rice, Mariee Grima, Nora E. Straznicky, Itamar Levinger, Elisabeth A. Lambert, Daniel J. van den Hoek, John B. Dixon
Trials.2016;[Epub] CrossRef - Semi-structured Interview Measure of Stigma (SIMS) in psychosis: Assessment of psychometric properties
Lisa Wood, Eilish Burke, Rory Byrne, Gabriela Enache, Anthony P. Morrison
Schizophrenia Research.2016; 176(2-3): 398. CrossRef - Measuring young women’s self-efficacy for healthy eating: Initial development and validation of a new questionnaire
Gregory Simmonds, Tannaze Tinati, Mary Barker, Felicity L Bishop
Journal of Health Psychology.2016; 21(11): 2503. CrossRef - Anxiety and Shame as Risk Factors for Depression, Suicidality, and Functional Impairment in Body Dysmorphic Disorder and Obsessive Compulsive Disorder
Hilary Weingarden, Keith D. Renshaw, Sabine Wilhelm, June P. Tangney, Jennifer DiMauro
Journal of Nervous & Mental Disease.2016; 204(11): 832. CrossRef - Child Sustained Attention in Preschool-Age Children
Cynthia F. DiCarlo, Jennifer J. Baumgartner, Carrie Ota, Kelly Geary
Journal of Research in Childhood Education.2016; 30(2): 143. CrossRef - Determinants and their causal relationships affecting the adoption of cloud computing in science and technology institutions
Bang-Ning Hwang, Chi-Yo Huang, Chia-Lee Yang
Innovation.2016; 18(2): 164. CrossRef - Determinants of subjective well‐being in people with psychosis referred for psychological therapy in South London
Annabel Broyd, Suzanne Jolley, Louise Johns
British Journal of Clinical Psychology.2016; 55(4): 429. CrossRef - Experiencing discomfort working alone on the night shift – Relations to shift work tolerance, personality, and work mastery
Ingvild Saksvik-Lehouillier
Scandinavian Psychologist.2015;[Epub] CrossRef - A study on the specificity of the association between hippocampal volume and delayed primacy performance in cognitively intact elderly individuals
Davide Bruno, Michel J. Grothe, Jay Nierenberg, Henrik Zetterberg, Kaj Blennow, Stefan J. Teipel, Nunzio Pomara
Neuropsychologia.2015; 69: 1. CrossRef - Construction of a lncRNA–PCG bipartite network and identification of cancer-related lncRNAs: a case study in prostate cancer
Yongjing Liu, Rui Zhang, Fujun Qiu, Kening Li, Yuanshuai Zhou, Desi Shang, Yan Xu
Molecular BioSystems.2015; 11(2): 384. CrossRef - How Much Is Too Much to Pay for Internet Access? A Behavioral Economic Analysis of Internet Use
Julie Broadbent, Michelle A. Dakki
Cyberpsychology, Behavior, and Social Networking.2015; 18(8): 457. CrossRef - Short and Long-term Effects of rTMS Treatment on Alzheimer's Disease at Different Stages: A Pilot Study
Grant Rutherford, Brian Lithgow, Zahra Moussavi
Journal of Experimental Neuroscience.2015;[Epub] CrossRef - Circadian preference and trait impulsivity, sensation-seeking and response inhibition in healthy young adults
Jee In Kang, Chun Il Park, Sung-yun Sohn, Hae Won Kim, Kee Namkoong, Se Joo Kim
Chronobiology International.2015; 32(2): 235. CrossRef - Is the data normally distributed?
C. Gissane
Physiotherapy Practice and Research.2015; 37(1): 57. CrossRef - The relationship between cerebrospinal fluid tau markers, hippocampal volume, and delayed primacy performance in cognitively intact elderly individuals
Davide Bruno, Michel J. Grothe, Jay Nierenberg, Stefan J. Teipel, Henrik Zetterberg, Kaj Blennow, Nunzio Pomara
Alzheimer's & Dementia: Diagnosis, Assessment & Disease Monitoring.2015; 1(1): 81. CrossRef - Association of metabolic acidosis with bovine milk-based human milk fortifiers
C C Cibulskis, E S Armbrecht
Journal of Perinatology.2015; 35(2): 115. CrossRef - Assessing antecedents and consequences of student satisfaction in higher education: evidence from Malaysia
M.M. Lai, S.H. Lau, N.A. Mohamad Yusof, K.W. Chew
Journal of Marketing for Higher Education.2015; 25(1): 45. CrossRef - Examining the Validity and Reliability of Antonovsky’s Sense of Coherence Scale in a Population of Pregnant Australian Women
Sally Ferguson, Deborah Davis, Jenny Browne, Jan Taylor
Evaluation & the Health Professions.2015; 38(2): 280. CrossRef - Acceptability of Functional Behavioral Assessment Procedures to Special Educators and School Psychologists
Robert E. O'neill, Kaitlin Bundock, Kristin Kladis, Leanne S. Hawken
Behavioral Disorders.2015; 41(1): 51. CrossRef - Single seed descent: a tool to exploit durum wheat (Triticum durum Desf.) genetic resources
Domenico Pignone, Domenico De Paola, Nicoletta Rapanà, Michela Janni
Genetic Resources and Crop Evolution.2015; 62(7): 1029. CrossRef - The more g-loaded, the more heritable, evolvable, and phenotypically variable: Homology with humans in chimpanzee cognitive abilities
Michael A. Woodley of Menie, Heitor B.F. Fernandes, William D. Hopkins
Intelligence.2015; 50: 159. CrossRef - Histogram Analysis of Gadoxetic Acid-Enhanced MRI for Quantitative Hepatic Fibrosis Measurement
Honsoul Kim, Seong Ho Park, Eun Kyung Kim, Myeong-Jin Kim, Young Nyun Park, Hae-Jeong Park, Jin-Young Choi, Do Young Kim
PLoS ONE.2014; 9(12): e114224. CrossRef - Postdoctoral Researchers in the UK: A Snapshot at Factors Affecting Their Research Output
Fatima M. Felisberti, Rebecca Sear, Vincent Larivière
PLoS ONE.2014; 9(4): e93890. CrossRef - Caregiver stress during the first year after diagnosis of an Autism Spectrum Disorder
John H. McGrew, Melissa L. Keyes
Research in Autism Spectrum Disorders.2014; 8(10): 1373. CrossRef - Recreational Drug Use and Fluctuating Asymmetry: Testing the Handicap Principle
Barbara Borkowska, Boguslaw Pawlowski
Evolutionary Psychology.2014; 12(4): 769. CrossRef - Execution of Diagnostic Testing Has a Stronger Effect on Emergency Department Crowding than Other Common Factors: A Cross-Sectional Study
Takahisa Kawano, Kei Nishiyama, Hiroyuki Hayashi, Robert Lane Schmidt
PLoS ONE.2014; 9(10): e108447. CrossRef - Validity of the trait emotional intelligence questionnaire in sports and its links with performance satisfaction
Sylvain Laborde, Fabrice Dosseville, Félix Guillén, Enrique Chávez
Psychology of Sport and Exercise.2014; 15(5): 481. CrossRef - Relation of Personality Traits and Students’ Academic Achievement
Rima Kratavičienė
Ugdymo psichologija.2014; 25: 74. CrossRef - Exercise Therapy in Hip Osteoarthritis
Inga Krauß, Benjamin Steinhilber, Georg Haupt, Regina Miller, Peter Martus, Pia Janßen
Deutsches Ärzteblatt international.2014;[Epub] CrossRef
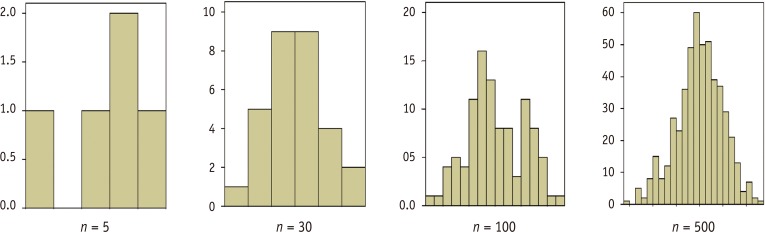
Figure 1
Skewness, kurtosis and normality tests for a characteristic of interests in various sizes of samples

*Lilliefors significance correct
*Lilliefors significance correct

 KACD
KACD
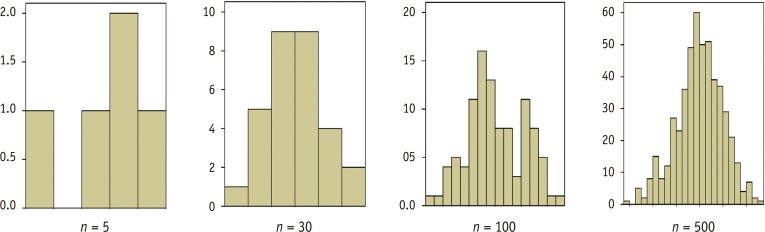

 ePub Link
ePub Link Cite
Cite