KACD
Articles
- Page Path
- HOME > Restor Dent Endod > Volume 37(4); 2012 > Article
- Open Lecture on Statistics Statistical notes for clinical researchers: assessing normal distribution (1)
- Hae-Young Kim
-
2012;37(4):-248.
DOI: https://doi.org/10.5395/rde.2012.37.4.245
Published online: November 21, 2012
Department of Dental Laboratory Science & Engineering, Korea University College of Health Science, Seoul, Korea. JFIF d d Ducky d qhttp://ns.adobe.com/xap/1.0/ |er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE &ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ >=F)2[nk؆?훐 M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag% qkEUzUgæBhߕP(7]kFnq?֖Cpru Z6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p \̅S?㭻;t~ R߁ )^/>Qj`yt[w ԛ;² ~+ ߔ_ YW~|o] ?x^ᯛ `ʼn;g)T@vWn]>&4l p+$D̢1l|ȨF%-} .9[}w~
ԠLM9hСablfe&QoW !s ?wjLK?s7yO>(=C~_nyǜu? v 3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw= /7ovuk+\V;lDgն <[A+r X~d;m!_s8ݖ;;.0llUC+?i#_crʙ1~C.\q u l8Hܶ2m`ܻM3Tov|Bs rɵ"oLS-
DКw=Tv@f '6|YlD͓Y%-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~
&f#
}o!muH; ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{
m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ
dng>ەZ,Mmϑ :n6nϦezW qUJ4! ۇ4R! =>>F n|Q[{pRO 17ƕ~._I ''00k=b՛o}Osðc2'o\3}ݭQ^ 2 . R1yKȣtAݿ-u ܾw!`?1Whn|gzU o[ECWwjUIן)^h#1ɭ!/Z
np;o;ΗŻkXs."6E`Z1
עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV 2`y/0E˛6+ԫ1?
6}KW c\KoKͨ2ۅFws*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* P RaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ
^˒4kƓmzDx
\
'Nq amP7nyN݅=
- Correspondence to Hae-Young Kim, PhD, DDS. Associate Professor, Department of Dental Laboratory Science & Engineering, Korea University College of Health Science, San 1 Jeongneung 3-dong, Seongbuk-gu, Seoul, Korea 136-703. TEL, +82-2-940-2845; FAX, +82-2-909-3502; kimhaey@korea.ac.kr
©Copyights 2012. The Korean Academy of Conservative Dentistry.
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
- 2,429 Views
- 42 Download
- 32 Crossref
1) Features of samples from normal populations
Various parametric tests make assumptions of the normal distribution, including t-test, analysis of variance (ANOVA), correlation, and regression. Different from some researcher's understanding, tests of normality are not for the normality of observed data but for normality of the population distribution of a random characteristic; e.g. assuming normality for the population distribution of the characteristic is reasonable when referring to the observed sample data. Actual distribution of the characteristic in a random sample chosen from a population with normal distribution doesn't appear normal, especially when the sample size is small (Figure 1). Distributions of larger samples tend to resemble the distribution of the characteristic in the population better by taking on a bell-shaped curve when the values of a characteristic in the population are plotted against their frequency.
2) Testing of the normality using SPSS statistical package
Using the SPSS output you can find out several methods to test normality of the data.
In SPSS you can find information needed for normality tests under the following menu:
Analysis - Descriptive Statistics - Explore
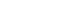
You can look at a histogram of your data and see whether the distribution of the sample resembles a normal distribution or not; e.g., whether the histogram looks like a bell-shape or not? Is the shape symmetrical or not? Or you can chose a Q-Q ("Q" stands for quantile) plot to see whether all the data points have a linear tendency and lie on the diagonal or not.
Most statistical packages provide both types of graphs. The advantage of the eyeball test is its easiness and simplicity and the disadvantage is that the criteria for determination are not clear.
Furthermore confusion arises from the fact that samples from a normal population don't necessarily show a normal distribution; few samples look like normal distributions, especially samples with small size, as we can see in Figure 1. Therefore this eyeball test may be more meaningful in relatively large samples (e.g., n > 50).
Generally formal normality tests such as the Shapiro-Wilk test or the Kolmogorov-Smirnov test have been well known. Those tests assess a null hypothesis that distribution of the data is normal. The Shapiro-Wilk test has been reported to be more powerful than the Kolmogorov-Smirnov test in testing normality (Razali et al., 2011).
3) Problems of formal normality tests
There are problems in formal normality tests that the probability of rejecting the null hypothesis of normality tends to slightly increase as sample size increases: for large samples (n > 300), these formal normality tests may be unreliable. Following example shows incompatible results in normality test for a large sample (n = 500). While the data seems to be approximately normal by an eyeball test, the Shapiro-Wilk test and Kolmogorov-Smirnov test give an opposite conclusion that the distribution of the data may be different from normality (p < 0.05).
Though methods above provide useful information, still it is not easy to determine whether the example data may satisfy the assumption of normal distribution or not. Confusion may arise because they suggest incompatible conclusions as shown above. More helpful methods to determine normality can be discussed at the next statistical note.
- 1. Razali NM, Wah YB. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anserson-Darling tests. J Stat Model Anal 2011;22:21-33.
REFERENCES
Tables & Figures
REFERENCES
Citations
Citations to this article as recorded by 
- Reliability and Validity Measures of the Patellofemoral Subscale KOOS-PF in Greek Patients with Patellofemoral Pain
Ioannis Moros, Eleni C. Boutsikari, George Plakoutsis, Elefterios Paraskevopoulos, George A. Koumantakis, Maria Papandreou
Journal of Functional Morphology and Kinesiology.2025; 10(1): 44. CrossRef - Relationships between nurses’ perceived social support, emotional labor, presenteeism, and psychiatric distress during the COVID-19 pandemic: a cross-sectional study
Hossein Ebrahimi, Farnaz Rahmani, Khadijeh Ghorbani
BMC Psychology.2025;[Epub] CrossRef - Enhancing employee well-being through a culturally adapted training program: a mixed-methods study in South Africa
Anurag Shekhar, Musawenkosi D. Saurombe, Renjini Mary Joseph
Frontiers in Public Health.2025;[Epub] CrossRef - Are There Sex Differences in Wrist Velocity and Forearm Muscle Activity When Performing Identical Hand-Intensive Work Tasks?
Gunilla Dahlgren, Per Liv, Fredrik Öhberg, Lisbeth Slunga Järvholm, Mikael Forsman, Börje Rehn
Sensors.2025; 25(17): 5517. CrossRef - The Joint Contributions of Foreign Language Enjoyment and Working Memory to Second Language Achievement
芷倩 陈
Advances in Psychology.2025; 15(09): 358. CrossRef - A comprehensive guide to selecting the right modeling strategy for explanatory and predictive data analysis
Maysa Niazy, Heather M. Murphy, Khurram Nadeem, Nicole Ricker
Canadian Journal of Microbiology.2025; 71: 1. CrossRef - The roles of social support, family support, coping strategies, and financial safety in posttraumatic growth among COVID-19 survivors in Kerala
Lijo Kochakadan Joy, Lincy Eralil Kunjumon, Anirudh Anil, Malavika Jaisankar, Aysha Fariha, Naziya Zaina Naufal, Swetha Pulikkal Santhosh, Anagha Kallazhi, Chee-Seng Tan
Current Psychology.2024; 43(19): 17766. CrossRef - The Gothenburg Trismus Questionnaire in China: Cross‐cultural adaptation and measurement invariance
Qian Zhang, Yao Feng, Ying‐Hui Zhou, Yi‐Fan Yang, Yun‐Zhi Feng, Yue Guo
Head & Neck.2024; 46(7): 1706. CrossRef - Shared benefits and sustainable mobility – A case of autonomous bus
Kari Koskinen, Niina Mallat, Bikesh Raj Upreti
Case Studies on Transport Policy.2024; 18: 101286. CrossRef - Comparison of perceived masticatory ability in completely edentulous patients treated with thermoplastic complete denture versus single implant-retained mandibular overdenture: a single-center prospective observational study
Mostafa I. Fayad, Ihab I. Mahmoud, Ahmed Atef Aly Shon, Mohamed Omar Elboraey, Ramy M. Bakr, Rania Moussa
PeerJ.2024; 12: e17670. CrossRef - The predictors of COVID-19 preventive health behaviors among adolescents: the role of health belief model and health literacy
Parvaneh Vasli, Zahra Shekarian-Asl, Mina Zarmehrparirouy, Meimanat Hosseini
Journal of Public Health.2024; 32(1): 157. CrossRef - A randomized controlled trial on the effects of traditional Thai mind-body exercise (Ruesi Dadton) on biomarkers in mild cognitive impairment
Phaksachiphon KHANTHONG, Kusuma SRIYAKUL, Ananya DECHAKHAMPHU, Aungkana KRAJARNG, Chuntida KAMALASHIRAN, Vadhana JAYATHAVAJ, Parunkul TUNGSUKRUTHAI
European Journal of Physical and Rehabilitation Medicine.2024;[Epub] CrossRef - Fighting Emerging Caspofungin-Resistant Candida Species: Mitigating Fks1-Mediated Resistance and Enhancing Caspofungin Efficacy by Chitosan
Aya Tarek, Yasmine H. Tartor, Mohamed N. Hassan, Ioan Pet, Mirela Ahmadi, Adel Abdelkhalek
Antibiotics.2024; 13(7): 578. CrossRef - Influence of Intraoperative Active and Passive Breaks in Simulated Minimally Invasive Procedures on Surgeons’ Perceived Discomfort, Performance, and Workload
Rosina Bonsch, Robert Seibt, Bernhard Krämer, Monika A. Rieger, Benjamin Steinhilber, Tessy Luger
Life.2024; 14(4): 426. CrossRef - Stay at home behavior during COVID-19: The role of person-home relationships
Silvia Ariccio, Annalisa Theodorou
Journal of Environmental Psychology.2024; 97: 102334. CrossRef - The impact of psychological distress, socio‐demographic and work‐related factors on coping strategies used by nurses during the COVID‐19 pandemic: A cross‐sectional study
Farnaz Rahmani, Fatemeh Ranjbar, Elnaz Asghari, Leila Gholizadeh
Nursing Open.2024;[Epub] CrossRef - A study protocol for a single-centred randomized trial to investigate the effect of pre-treatment communication methods on dental anxiety among adult dental patients
Shakeerah Olaide Gbadebo, Gbemisola Aderemi Oke, Oluwole Oyekunle Dosumu
SAGE Open Medicine.2023;[Epub] CrossRef - Development, validation and psychometric evaluation of the Chinese version of the biopsychosocial impact scale in orofacial pain patients
Ze-Yue Ou-Yang, Yao Feng, Dong-Dong Xie, Yi-Fan Yang, Yun Chen, Ning-Xin Chen, Xiao-Lin Su, Bi-Fen Kuang, Jie Zhao, Ya-Qiong Zhao, Yun-Zhi Feng, Yue Guo
Frontiers in Psychology.2023;[Epub] CrossRef - Using a Back Exoskeleton During Industrial and Functional Tasks—Effects on Muscle Activity, Posture, Performance, Usability, and Wearer Discomfort in a Laboratory Trial
Tessy Luger, Mona Bär, Robert Seibt, Monika A. Rieger, Benjamin Steinhilber
Human Factors: The Journal of the Human Factors and Ergonomics Society.2023; 65(1): 5. CrossRef - Impact of door in-door out time on total ischemia time and clinical outcomes in patients with ST-elevation myocardial infarction
Cátia Costa Oliveira, Miguel Afonso, Carlos Braga, João Costa, Jorge Marques
Revista Portuguesa de Cardiologia.2023; 42(2): 101. CrossRef - Measuring the service quality of governmental sites: Development and validation of the e-Government service quality (EGSQUAL) scale
Muhammad Aljukhadar, Jean-François Belisle, Danilo C. Dantas, Sylvain Sénécal, Ryad Titah
Electronic Commerce Research and Applications.2022; 55: 101182. CrossRef - Exploratory and Confirmatory Factor Analysis for Disposition Levels of Computational Thinking Instrument Among Secondary School Students
Saralah Sovey, Kamisah Osman, Mohd Effendi Ewan Mohd-Matore
European Journal of Educational Research.2022; volume-11-(volume-11-): 639. CrossRef - The Development and Psychometric Assessment of Malaysian Youth Adversity Quotient Instrument (MY-AQi) by Combining Rasch Model and Confirmatory Factor Analysis
Mohd Effendi Ewan Mohd Matore, Mohammed Afandi Zainal, Muhamad Firdaus Mohd Noh, Ahmad Zamri Khairani, Nordin Abd Razak
IEEE Access.2021; 9: 13314. CrossRef - Enhancing celebrity fan-destination relationship in film-induced tourism: The effect of authenticity
Hsiu-Yu Teng, Chien-Yu Chen
Tourism Management Perspectives.2020; 33: 100605. CrossRef - Sex differences in muscle activity and motor variability in response to a non-fatiguing repetitive screwing task
Tessy Luger, Robert Seibt, Monika A. Rieger, Benjamin Steinhilber
Biology of Sex Differences.2020;[Epub] CrossRef - Physiological changes during prolonged standing and walking considering age, gender and standing work experience
Rudolf Wall, Gabriela Garcia, Thomas Läubli, Robert Seibt, Monika A. Rieger, Bernard Martin, Benjamin Steinhilber
Ergonomics.2020; 63(5): 579. CrossRef - Is the Arrhenius-correction of biodegradation rates, as recommended through REACH guidance, fit for environmentally relevant conditions? An example from petroleum biodegradation in environmental systems
David M. Brown, Louise Camenzuli, Aaron D. Redman, Chris Hughes, Neil Wang, Eleni Vaiopoulou, David Saunders, Alex Villalobos, Susannah Linington
Science of The Total Environment.2020; 732: 139293. CrossRef - The Role of Motor Learning on Measures of Physical Requirements and Motor Variability During Repetitive Screwing
Tessy Luger, Robert Seibt, Monika A. Rieger, Benjamin Steinhilber
International Journal of Environmental Research and Public Health.2019; 16(7): 1231. CrossRef - Influence of a passive lower-limb exoskeleton during simulated industrial work tasks on physical load, upper body posture, postural control and discomfort
Tessy Luger, Robert Seibt, Timothy J. Cobb, Monika A. Rieger, Benjamin Steinhilber
Applied Ergonomics.2019; 80: 152. CrossRef - Efficacy of Epithelium-Off and Epithelium-On Corneal Collagen Cross-Linking in Pediatric Keratoconus
Muhsin Eraslan, Ebru Toker, Eren Cerman, Deniz Ozarslan
Eye & Contact Lens: Science & Clinical Practice.2017; 43(3): 155. CrossRef - Failure to Replicate the Structure of a Spanish-Language Brief Wisconsin Inventory of Smoking Dependence Motives Across Three Samples of Latino Smokers
Yessenia Castro, Virmarie Correa-Fernández, Miguel Á. Cano, Carlos Mazas, Karla Gonzalez, Damon J. Vidrine, Jennifer I. Vidrine, David W. Wetter
Nicotine & Tobacco Research.2014; 16(9): 1277. CrossRef - A cross-lagged path analysis of five intrapersonal determinants of smoking cessation
Yessenia Castro, Miguel Ángel Cano, Michael S. Businelle, Virmarie Correa-Fernández, Whitney L. Heppner, Carlos A. Mazas, David W. Wetter
Drug and Alcohol Dependence.2014; 137: 98. CrossRef
ePub Link
Cite
XML DownloadStatistical notes for clinical researchers: assessing normal distribution (1)
Figure 1 Histograms of a characteristic of interest in various sizes of random samples from a normal population (N = 10,000) with a normal distribution (sample size = 3, 5, 10, 30, 100 and 500).
Figure 1
Statistical notes for clinical researchers: assessing normal distribution (1)
