Rheological characterization of composites using a vertical oscillation rheometer

In-Bog Lee; Byung-Hoon Cho; Ho-Hyun Son; Sang-Tag Lee; Chung-Moon Um

doi:10.5395/JKACD.2004.29.6.489

Articles

Page Path: HOME > Restor Dent Endod > Volume 29(6); 2004 > Article

Original Article Rheological characterization of composites using a vertical oscillation rheometer: In-Bog Lee, Byung-Hoon Cho, Ho-Hyun Son, Sang-Tag Lee, Chung-Moon Um; Journal of Korean Academy of Conservative Dentistry 2004;29(6):489-497.
DOI: https://doi.org/10.5395/JKACD.2004.29.6.489
Published online: November 30, 2004

Department of Conservative Dentistry, College of Dentistry, Seoul National University, Korea.

Corresponding author: Chung-Moon Um. Department of Conservative Dentistry, College of Dentistry, Seoul National University, 28 Yoengun-dong, Chongro-gu, Seoul, Korea, 110-749. Tel: 82-2-2072-3953, 2651, Fax: 82-2-2072-3859, inboglee@snu.ac.kr

15 Views
0 Download

prev next

Full Article

Download PDF

Abstract
REFERENCES

Abstract

Objective
The purpose of this study was to investigate the viscoelastic properties related to handling characteristics of composite resins.
Methods
A custom designed vertical oscillation rheometer (VOR) was used for rheological measurements of composites. The VOR consists of three parts: (1) a measuring unit, (2) a deformation induction unit and (3) a force detecting unit. Two medium viscous composites, Z100 and Z250 and two packable composites, P60 and SureFil were tested. The viscoelastic material function, including complex modulus E^* and phase angle δ, were measured. A dynamic oscillatory test was used to evaluate the storage modulus (E'), loss modulus (E") and loss tangent (tanδ) of the composites as a function of frequency (ω) from 0.1 to 20 H_z at 23℃.
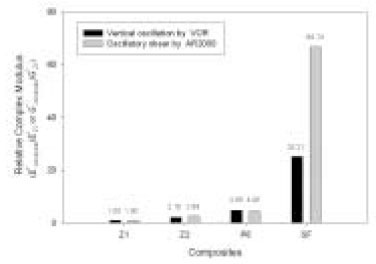
Results
The E' and E" increased with increasing frequency and showed differences in magnitude between brands. The E^*s of composites at ω = 2 H_z, normalized to that of Z100, were 2.16 (Z250), 4.80 (P60) and 25.21 (SureFil). The magnitudes and patterns of the change of tanδ of composites with increasing frequency were significantly different between brands. The relationships between the complex modulus E^*, the phase angle δ and the frequency ω were represented by frequency domain phasor form, E^* (ω) = E^*e^iδ = E^*∠δ.
Conclusions
The viscoelasticity of composites that influences handling characteristics is significant different between brands. The VOR is a relatively simple device for dynamic, mechanical analysis of high viscous dental composites. The locus of frequency domain phasor plots in a complex plane is a valuable method of representing the viscoelastic properties of composites.
Keywords: VOR; Viscoelasticity; Composite; Complex modulus; Frequency domain phasor plot

REFERENCES

1. Craig RG, Powers JM. Restorative dental materials. 2002;11th ed. Mosby co; 91-98. 231-251.
2. Bayne SC, Thompson JY, Swift EJ, et al. A characterization of first-generation flowable composites. J Am Dent Assoc. 1998;129: 567-577.PubMed
3. Leinfelder KF, Prasad A. A new condensable composite for the restoration of posterior teeth. Dent Today. 1998;17(2):112-116.
4. Leinfelder KF, Radz GM, Nash RW. A report on a new condensable composite resin. Compendium. 1998;19(3):230-237.PubMed
5. Opdam NJM, Roeters JJM, Peters TCRB, et al. Consistency of resin composites for posterior use. Dent Mater. 1996;12: 350-354.Article PubMed
6. Ferracane JL, Moser JB, Greener EH. Rheology of composite restoratives. J Dent Res. 1981;60(9):1678-1685.PubMed
7. Tyas MJ, Jones DW, Rizkalla AS. The evaluation of resin composite consistency. Dent Mater. 1998;14: 424-428.Article PubMed
8. Al-sharaa KA, Watts DC. Stickiness prior to setting of some light cured resin composites. Dent Mater. 2003;19: 182-187.Article PubMed
9. Willems G, Lambrechts P, Braaem M, et al. A classification of dental composites according to their morphological and mechanical characteristics. Dent Mater. 1992;8: 310-319.Article PubMed
10. Duran RL, Powers JM, Craig RG. Viscoelastic and dynamic properties of soft liners and tissue conditioners. J Dent Res. 1979;58(8):1801-1807.PubMed
11. Goldberg AJ. Viscoelastic properties of silicon, polysulfide, and polyether impression materials. J Dent Res. 1974;53(5):1033-1039.Article PubMed PDF
12. Watts DC. Elastic moduli and visco-elastic relaxation. J Dent. 1994;22: 154-158.Article PubMed
13. McCabe JF, Bowman AJ. The rheological properties of dental impression materials. Brit dent J. 1981;151: 179.Article PubMed PDF
14. Jacobsen PH, Whiting R, Richardson PCA. Viscosity of setting anterior restorative materials. Brit dent J. 1977;143: 393.PubMed
15. Braden M. Viscosity and consistency of impression rubbers. J Dent Res. 1967;46(2):429-433.Article PubMed PDF
16. Barnes HA, Hutton JF, Walters K. An introduction to rheology. 1989;Elsevier Science Publishing co.
17. Moon TJ. Rheology. 1988;1st ed. Minumsa; 7-80. 190-195.
18. Kim SY. Polymer physics. 1994;2nd ed. Seoul University Press; 7-26.
19. Lee IB, Son HH, Um CM. Rheological Properties of flowable, conventional hybrid, and condensable composite resins. Dent Mater. 2003;19: 298-307.PubMed
20. Kim JW, Cho MS, Choi HJ, et al. Electrorheological fluid characterization via a vertical oscollation rheometer. Polym Test. 2001;20: 913-918.
21. Cho MS, Choi YJ, Choi SG, et al. Viscoelasticity of an electrorheological fluid using a vertical oscillation rheometer. J Mol Liq. 1998;75: 13-24.
22. Hyeon JC, et al. Theories and Applications of Rheology. 2001;1st ed. The Korean Society of Rheology; 237-239.

Figure 1-a

Diagram of the VOR (vertical oscillatory rheometer)

Figure 1-b

The geometry of measuring unit

Figure 2

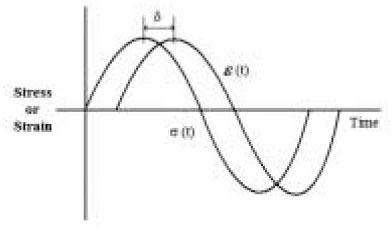
The relationship between strain ε(t), stress σ(t) and phase angle δ in dynamic oscillatory test

Figure 3

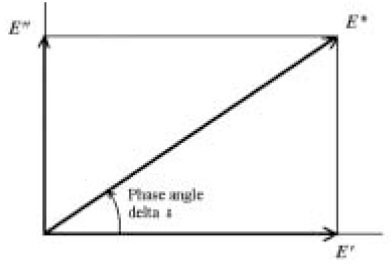
The relationship between storage (real) modulus E', loss modulus (imaginary) modulus E", complex modulus E^* and phase angle δ in a complex plane

Figure 4

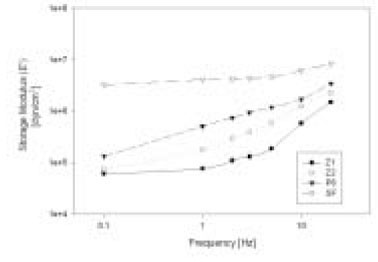
Storage modulus E' increased with increasing the frequency and showed differences in magnitude between brands

Figure 5

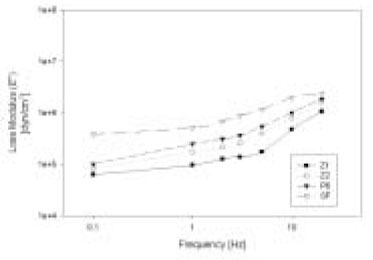
Loss modulus E" increased with increasing the frequency and showed differences in magnitude between brands

Figure 6

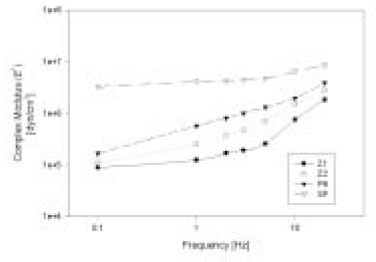
Complex modulus E^* increased with increasing the frequency and showed differences in magnitude between brands

Figure 7

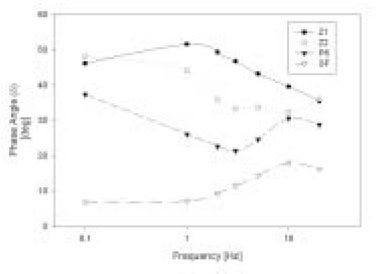
Phase angle δ of composite. The patterns of the change of δ of samples with increasing frequency showed the different characteristics of the composites between brands

Figure 8

Loss tangent as a function of frequency

Figure 9

Relative complex modulus of composites normalized to that of Z1 at ω = 2 Hz

Figure 10

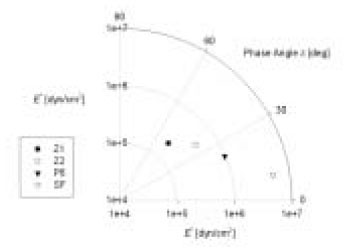
Phasor presentation of E^* and δ, E^*e^iδ= E^*∠δ, of composites at ω = 2 Hz in a polar coordinate system

Figure 11

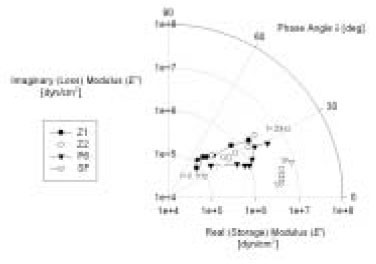
Locus of frequency domain phasor plots, G^*(ω)e^iδ = ∣ G^*(ω) ∣ ∠δ of composites in a complex plane

Table 1

Phasor presentation of the complex modulus E^* and phase angle (δ) of composite resins at various frequencies, E^* (dyn/cm²) ∠δ(°)

Table 2

Phasor presentation of the complex shear modulus G^* and phase angle (δ) of composite resins at various frequencies, G^* (dyn/cm²) ∠δ(°)

Tables & Figures

REFERENCES

Citations

Citations to this article as recorded by

ePub Link

Cite

CITE: export Copy Download Format; Close

Download Citation

Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.

Format:

RIS — For EndNote, ProCite, RefWorks, and most other reference management software
BibTeX — For JabRef, BibDesk, and other BibTeX-specific software

Include:

Citation for the content below
Citation and abstract for the content below

Rheological characterization of composites using a vertical oscillation rheometer

J Korean Acad Conserv Dent. 2004;29(6):489-497. Published online November 30, 2004

DOI: https://doi.org/10.5395/JKACD.2004.29.6.489

XML Download

Figure

Rheological characterization of composites using a vertical oscillation rheometer

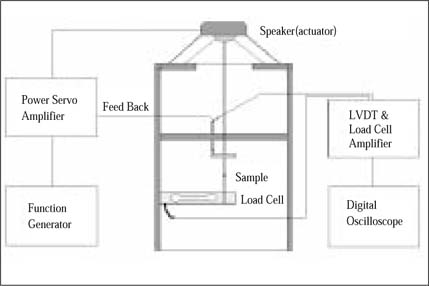
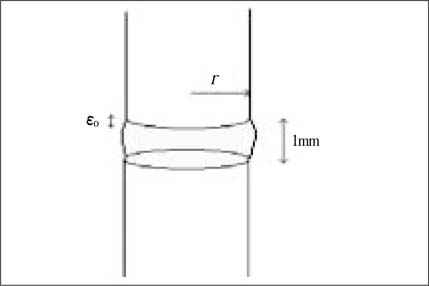
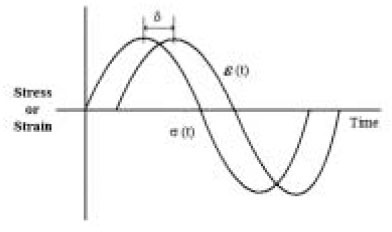
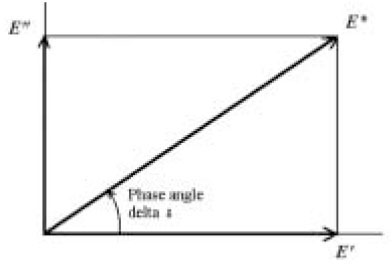
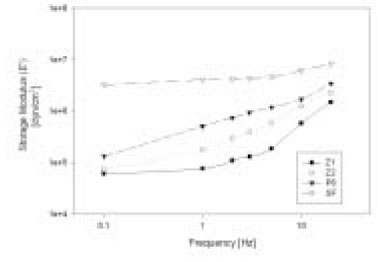
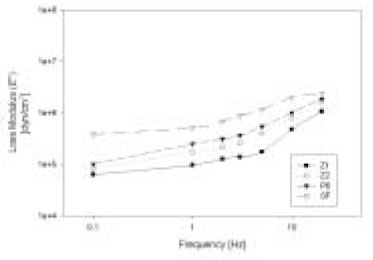
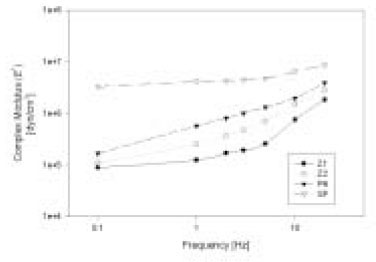
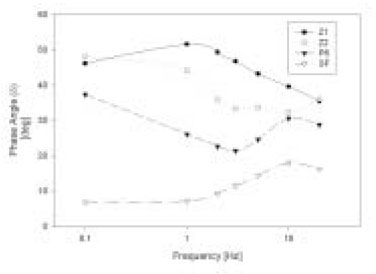
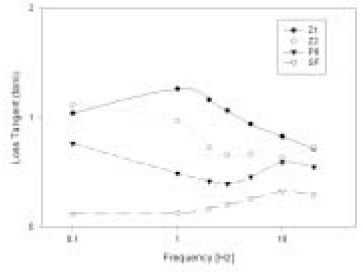
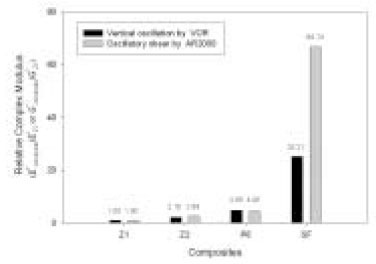
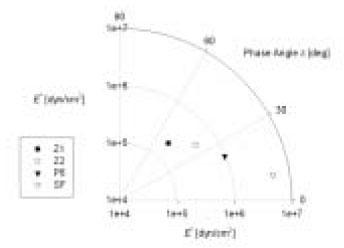
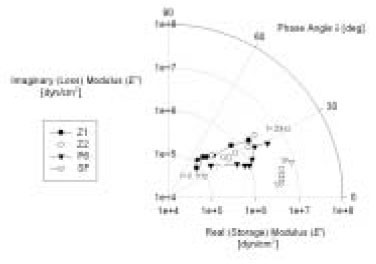
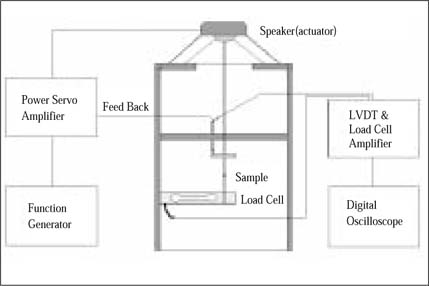
Figure 1-a Diagram of the VOR (vertical oscillatory rheometer)

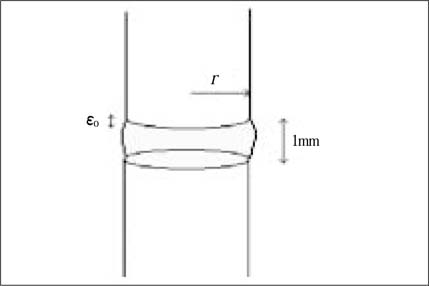
Figure 1-b The geometry of measuring unit

Figure 2 The relationship between strain ε(t), stress σ(t) and phase angle δ in dynamic oscillatory test

Figure 3 The relationship between storage (real) modulus E', loss modulus (imaginary) modulus E", complex modulus E* and phase angle δ in a complex plane

Figure 4 Storage modulus E' increased with increasing the frequency and showed differences in magnitude between brands

Figure 5 Loss modulus E" increased with increasing the frequency and showed differences in magnitude between brands

Figure 6 Complex modulus E* increased with increasing the frequency and showed differences in magnitude between brands

Figure 7 Phase angle δ of composite. The patterns of the change of δ of samples with increasing frequency showed the different characteristics of the composites between brands

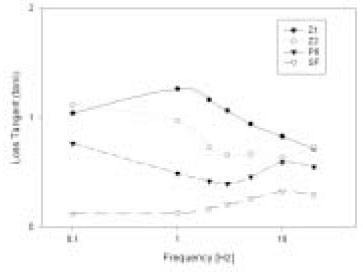
Figure 8 Loss tangent as a function of frequency

Figure 9 Relative complex modulus of composites normalized to that of Z1 at ω = 2 Hz

Figure 10 Phasor presentation of E* and δ, E*eiδ= E*∠δ, of composites at ω = 2 Hz in a polar coordinate system

Figure 11 Locus of frequency domain phasor plots, G*(ω)eiδ = ∣ G*(ω) ∣ ∠δ of composites in a complex plane

Figure 1-a

Figure 1-b

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6

Figure 7

Figure 8

Figure 9

Figure 10

Figure 11

Rheological characterization of composites using a vertical oscillation rheometer

Table 1

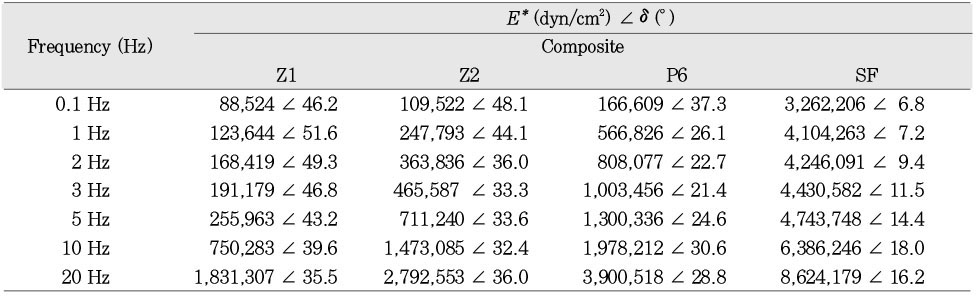
Phasor presentation of the complex modulus E^* and phase angle (δ) of composite resins at various frequencies, E^* (dyn/cm²) ∠δ(°)

Table 2

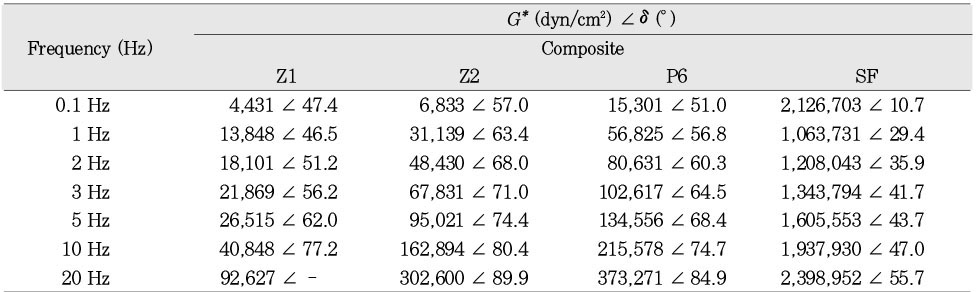
Phasor presentation of the complex shear modulus G^* and phase angle (δ) of composite resins at various frequencies, G^* (dyn/cm²) ∠δ(°)

Table 1 Phasor presentation of the complex modulus E* and phase angle (δ) of composite resins at various frequencies, E* (dyn/cm2) ∠δ(°)

Table 2 Phasor presentation of the complex shear modulus G* and phase angle (δ) of composite resins at various frequencies, G* (dyn/cm2) ∠δ(°)