Articles
- Page Path
- HOME > Restor Dent Endod > Volume 40(1); 2015 > Article
- Open Lecture on Statistics Statistical notes for clinical researchers: A one-way repeated measures ANOVA for data with repeated observations
- Hae-Young Kim
-
2015;40(1):-95.
DOI: https://doi.org/10.5395/rde.2015.40.1.91
Published online: January 12, 2015
Department of Dental Laboratory Science and Engineering, College of Health Science & Department of Public Health Science, Graduate School, Korea University, Seoul, Korea.
- Correspondence to Hae-Young Kim, DDS, PhD. Associate Professor, Department of Dental Laboratory Science & Engineering, Korea University College of Health Science, San 1 Jeongneung 3-dong, Seongbuk-gu, Seoul, Korea 136-703. TEL, +82-2-940-2845; FAX, +82-2-909-3502, kimhaey@korea.ac.kr
©Copyrights 2015. The Korean Academy of Conservative Dentistry.
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
- 7,264 Views
- 100 Download
- 28 Crossref
Repeated measures and correlated data
Repeated measurements can be obtained in many situations. A simple example is a pre-post design to assess the intervention effect. With respect to conditions, e.g., treatment A, B, and C, different treatments may be applied to the same group of subjects repeatedly according to the designated time schedule to compare the effects of treatments. In perspective of time, we may measure children's height repeatedly to know the growth pattern. In the field of dentistry, we measure the periodontal pocket depths of a tooth repeatedly at different surfaces: buccal, lingual, mesial, and distal. Common characteristics of these repeated measurements include correlations of the data points obtained by the same object, person, tooth, etc. The paired t-test is an analyzing method of correlated samples with two time points or occasions. For three or more time points or repeated conditions, we may use the repeated measures ANOVA which is equivalent to the one-way ANOVA for independent samples. Therefore, continuous outcome variables and categorical independent variables are the basic requirements.
Comparison of one-way repeated measures ANOVA and classical one-way ANOVA
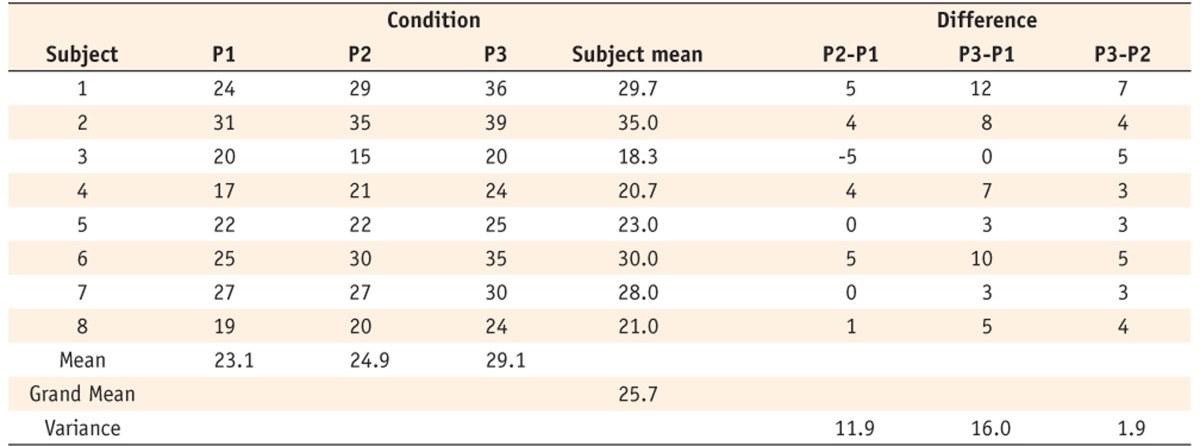
Table 1 shows a hypothetical data with repeated observations, P1, P2, and P3, which may represent scores measured in different conditions or different time points. If we disregard the correlated structure of three scores, the data can be analyzed using the one-way ANOVA. The classical one-way ANOVA decomposes the total variation of scores (SST, total sum of squares) into between-group variance (SSB, SS by conditions in Table 2) and within-group variance (SSW, SS residual in Table 2). The total variation is explained by SSB of different conditions (P1, P2, and P3), and the remainder is a substantial amount of unexplained within-group variance (Table 2). On the other hand, in the one-way repeated measures ANOVA, SSW is divided into SS by subject and unexplained SS (SSE, error sum of squares), which results in a significant difference among different conditions after considering subject effects, as shown in Table 3. In the classical ANOVA, different conditions do not make significant differences (p = 0.1503), while the repeated measures ANOVA obtain significant differences (p < 0.0001). The variance proportion explained in ANOVA is used as an 'effect size' which represents the degree how the analysis is effective in explaining the variance of outcome variable. In result of the repeated measures ANOVA, 'the partial eta squared' is calculated by dividing the variance explained with the condition (SS by condition) by the total variance (SS by condition +SS residual), excluding variance by subjects. In Table 3, the partial eta squared is calculated as 0.69.
Multivariate and univariate tests
The multivariate tests analyze multiple variables (P1, P2, P3) as one observation using a 'wide-form' data that one person has one record with P1 to P3. The multivariate approach requires a sufficient number of subjects (e.g., larger than 30) as the number of person is the number of information. Also a record with any missing value is deleted, therefore even small number of missing values may lead to substantial loss of information. When sample size is large, Pillai's trace and Wilk's lambda have similar power and show similar results (Please refer [g] of SPSS analysis results).1 The univariate tests are analyzing 'long form' data that one person has multiple records by occasions, e.g., three records per person in this example. The univariate tests have more power based on the increased number of information and have relative advantage in treating missing values that only the missing occasions are deleted. In case with many missing values, only the univariate approach works. However additional assumption, 'sphericity' is enquired to obtain reasonable analysis results by the univariate tests.
Sphericity assumption of univariate tests
The univariate tests assume an equal correlation between the repeated measures which is called 'sphericity' condition. Sphericity refers to the condition where the variances of the differences between all possible pairs of groups (i.e., levels of the independent variable, 'conditions' here) are equal. Table 3 is the result based on the sphericity assumption. However, variances in differences between pairs of conditions, P2-P1, P3-P1, and P3-P2 are 11.9, 16.0, and 1.9, respectively, which seem fairly different (shown in the right side of Table 1). The Mauchly's test which evaluates the sphericity condition showed that the assumption of sphericity was unsatisfied (p = 0.025, [h] of SPSS results), thus additional remedy steps should be taken. The remedy is to adjust degrees of freedom of numerator and denominator by multiplying the adjustment factor, ε (epsilon). Two kinds of epsilon, Greenhouse-Geisser and Huynh-Feldt epsilon ([h] of SPSS results) are applied to the test of within-subject effect ([i] of SPSS results). If the epsilon is close to one, which means the sphericity assumption is met, then there is no need of adjustment. The guideline of epsilon is determined by the Greenhouse-Geisser epsilon, 0.75; if larger than 0.75 then apply the Huynh-Feldt epsilon, otherwise, apply the Greenhouse-Geisser epsilon.2 In this example as the Greenhouse-Geisser epsilon was 0.586, we interpret the corrected results in (i) of the SPSS results by applying epsilon to degrees of freedom of 'repeat 1' and error portion (p = 0.003) with the heading Greenhouse-Geisser. The pairwise comparison of main effects of P1, P2, and P3 shows that significant differences are found in P3 and other two occasions by applying the Bonferroni correction which controls the type one error rate ([k] of SPSS results). We could see that mean of P3 is significantly different from those of P1 (p = 0.011) and P2 (p < 0.001), while means of P1 and P2 are similar (p = 0.585) as shown in table (k) of SPSS output.
Other outputs
Assessment polynomial terms show that assuming linear relationship among repeated measurements is appropriate ([j] of SPSS results). Also the Profile plot ([l] of SPSS results) provides the trend of the repeated measurements. Tests of between-subjects effects traditionally provided by the repeated measures ANOVA SPSS output (not shown) represent the comparison of simple averaged values among groups without accounting for correlated structures; therefore the importance of the result is little in respect to the analysis of correlated data.
The procedure of the one-way repeated measures ANOVA using SPSS statistical package (SPSS Inc., Chicago, IL, USA):
Tables & Figures
REFERENCES
Citations
Citations to this article as recorded by 

- The Distorting Influence of Primacy Effects on Reporting Cognitive Load in Learning Materials of Varying Complexity
Felix Krieglstein, Maik Beege, Lukas Wesenberg, Günter Daniel Rey, Sascha Schneider
Educational Psychology Review.2025;[Epub] CrossRef - Systemically circulating 17β-estradiol enhances the neuroprotective effect of the smoking cessation drug cytisine in female parkinsonian mice
Sara M. Zarate, Roger C. Garcia, Gauri Pandey, Rahul Srinivasan
npj Parkinson's Disease.2025;[Epub] CrossRef - Basic Statistics for Radiologists: Part 1—Basic Data Interpretation and Inferential Statistics
Adarsh Anil Kumar, Jineesh Valakkada, Anoop Ayyappan, Santhosh Kannath
Indian Journal of Radiology and Imaging.2025; 35(S 01): S58. CrossRef - How much missing data is too much to impute for longitudinal health indicators? A preliminary guideline for the choice of the extent of missing proportion to impute with multiple imputation by chained equations
K. P. Junaid, Tanvi Kiran, Madhu Gupta, Kamal Kishore, Sujata Siwatch
Population Health Metrics.2025;[Epub] CrossRef - Exploring nightly variability and clinical influences on sleep measures: insights from a digital brain health platform
Huitong Ding, Sanskruti Madan, Edward Searls, Matthew McNulty, Spencer Low, Zexu Li, Kristi Ho, Salman Rahman, Akwaugo Igwe, Zachary Popp, Phillip H. Hwang, Ileana De Anda-Duran, Vijaya B. Kolachalama, Jesse Mez, Michael L. Alosco, Robert J. Thomas, Rhoda
Sleep Medicine.2025; 131: 106532. CrossRef - Proposed Standard Test to Evaluate Back-Support Exoskeleton Efficacy for Rebar Workers: Test Design and Initial Implementation
Malcolm Dunson-Todd, Mazdak Nik-Bakht, Amin Hammad
Journal of Computing in Civil Engineering.2025;[Epub] CrossRef - Analysis of interaction effect between within- and between-subject factors in repeated measures analysis of variance for longitudinal data
Jonghae Kim, Jae Hong Park, Tae Kyun Kim
Korean Journal of Anesthesiology.2025; 78(5): 418. CrossRef - Assessing the Quality of World Health Organisation Guidelines during Health Emergencies: A Domain-Based Analysis
Bernard Ayine, Cornelius Fuumaale Suom-Kogle
Journal of Epidemiology and Global Health.2025;[Epub] CrossRef - Appraising the Factors Associated with Delirium Care Behaviours and Barriers to Their Assessment Among Clinical Nurses: A Cross-Sectional Study
Susan Ka Yee Chow, Soi Chu Chan
International Journal of Environmental Research and Public Health.2024; 21(12): 1582. CrossRef - Partitioning for Enhanced Statistical Power and Noise Reduction: Comparing One-Way and Repeated Measures Analysis of Variance (ANOVA)
Frederick Strale
Cureus.2024;[Epub] CrossRef - Development of a near infrared region based non-invasive therapy device for diabetic peripheral neuropathy
S. V. K. R. Rajeswari, Vijayakumar Ponnusamy, Nemanja Zdravkovic, Emilija Kisic, V. Padmajothi, S. Vijayalakshmi, C. Anuradha, D. Malathi, Nandakumar Ramasamy, Kumar Janardhan, Melvin George
Scientific Reports.2024;[Epub] CrossRef - Influence of membrane pore-size on the recovery of endogenous viruses from wastewater using an adsorption-extraction method
Warish Ahmed, Wendy J.M. Smith, Kwanrawee Sirikanchana, Masaaki Kitajima, Aaron Bivins, Stuart L. Simpson
Journal of Virological Methods.2023; 317: 114732. CrossRef - The effect of objective structured clinical examinations for nursing students
Eun-Ho Ha, Eunju Lim, Atiyeh Abdallah
PLOS ONE.2023; 18(6): e0286787. CrossRef - Myotomy and EndoFLIP: repeated measurements require a different statistical test
Nitin Jagtap, C. Sai Kumar, Rakesh Kalapala, D. Nageshwar Reddy
Gastrointestinal Endoscopy.2022; 95(4): 810. CrossRef - Training History, Cardiac Autonomic Recovery from Submaximal Exercise and Associated Performance in Recreational Runners
Matic Špenko, Ivana Potočnik, Ian Edwards, Nejka Potočnik
International Journal of Environmental Research and Public Health.2022; 19(16): 9797. CrossRef - Real-time vehicular accident prevention system using deep learning architecture
Md Faysal Kabir, Sahadev Roy
Expert Systems with Applications.2022; 206: 117837. CrossRef - Redesigning navigational aids using virtual global landmarks to improve spatial knowledge retrieval
Jia Liu, Avinash Kumar Singh, Anna Wunderlich, Klaus Gramann, Chin-Teng Lin
npj Science of Learning.2022;[Epub] CrossRef - Modeling the Progression of Speech Deficits in Cerebellar Ataxia Using a Mixture Mixed-Effect Machine Learning Framework
Bipasha Kashyap, Pubudu N. Pathirana, Malcolm Horne, Laura Power, David J. Szmulewicz
IEEE Access.2021; 9: 135343. CrossRef - Physiologic Characteristics of Hyperosmolar Therapy After Pediatric Traumatic Brain Injury
Jeffrey Wellard, Michael Kuwabara, P. David Adelson, Brian Appavu
Frontiers in Neurology.2021;[Epub] CrossRef - Effects of Brain Breaks Video Intervention of Decisional Balance among Malaysians with Type 2 Diabetes Mellitus: A Randomised Controlled Trial
Aizuddin Hidrus, Yee Cheng Kueh, Bachok Norsa’adah, Yu-Kai Chang, Garry Kuan
International Journal of Environmental Research and Public Health.2021; 18(17): 8972. CrossRef - Inter-study repeatability of circumferential strain and diastolic strain rate by CMR tagging, feature tracking and tissue tracking in ST-segment elevation myocardial infarction
Sheraz A. Nazir, Abhishek M. Shetye, Jamal N. Khan, Anvesha Singh, Jayanth R. Arnold, Iain Squire, Gerry P. McCann
The International Journal of Cardiovascular Imaging.2020; 36(6): 1133. CrossRef - Coagulation FXIII-A Protein Expression Defines Three Novel Sub-populations in Pediatric B-Cell Progenitor Acute Lymphoblastic Leukemia Characterized by Distinct Gene Expression Signatures
Katalin Gyurina, Bettina Kárai, Anikó Ujfalusi, Zsuzsanna Hevessy, Gábor Barna, Pál Jáksó, Gyöngyi Pálfi-Mészáros, Szilárd Póliska, Beáta Scholtz, János Kappelmayer, Gábor Zahuczky, Csongor Kiss
Frontiers in Oncology.2019;[Epub] CrossRef - Investigation of Longitudinal Data Analysis: Hierarchical Linear Model and Latent Growth Model Using a Longitudinal Nursing Home Dataset
Juh Hyun Shin, In-Soo Shin
Research in Gerontological Nursing.2019; 12(6): 275. CrossRef - Combining Microfractures, Autologous Bone Graft, and Autologous Matrix-Induced Chondrogenesis for the Treatment of Juvenile Osteochondral Talar Lesions
Riccardo D’Ambrosi, Camilla Maccario, Chiara Ursino, Nicola Serra, Federico Giuseppe Usuelli
Foot & Ankle International.2017; 38(5): 485. CrossRef - The assumption of sphericity in repeated-measures designs: What it means and what to do when it is violated
David M. Lane
The Quantitative Methods for Psychology.2016; 12(2): 114. CrossRef - Regional Coherence Alterations Revealed by Resting-State fMRI in Post-Stroke Patients with Cognitive Dysfunction
Cheng-Yu Peng, Yu-Chen Chen, Ying Cui, Deng-Ling Zhao, Yun Jiao, Tian-Yu Tang, Shenghong Ju, Gao-Jun Teng, Xi-Nian Zuo
PLOS ONE.2016; 11(7): e0159574. CrossRef - Evaluation of an Ophthalmic Anesthesia Simulation System for Regional Block Training
Biswarup Mukherjee, Jaichandran V. Venkatakrishnan, Boby George, Mohanasankar Sivaprakasam
Ophthalmology.2015; 122(12): 2578. CrossRef - What repeated measures analysis of variances really tells us
Younsuk Lee
Korean Journal of Anesthesiology.2015; 68(4): 340. CrossRef
Statistical notes for clinical researchers: A one-way repeated measures ANOVA for data with repeated observations
Statistical notes for clinical researchers: A one-way repeated measures ANOVA for data with repeated observations
Hypothetical data with repeated observations
Summary table for the classical on-way ANOVA (incorrect)

Summary table for the one-way repeated measures ANOVA
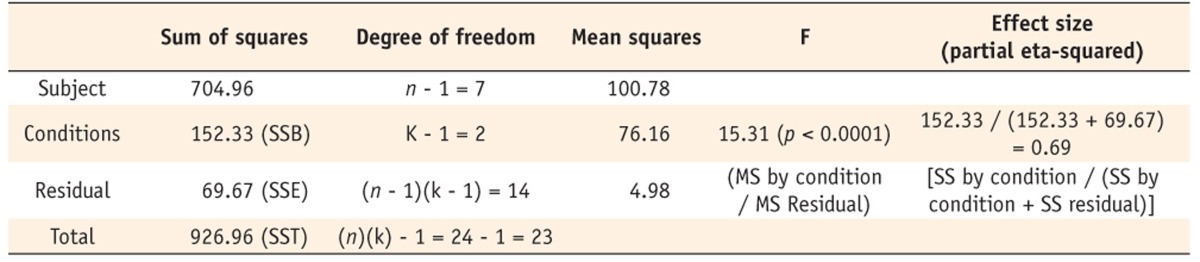
Table 1 Hypothetical data with repeated observations
Table 2 Summary table for the classical on-way ANOVA (incorrect)
Table 3 Summary table for the one-way repeated measures ANOVA

 KACD
KACD



 ePub Link
ePub Link Cite
Cite