Statistical notes for clinical researchers: Evaluation of measurement error 2: Dahlberg's error, Bland-Altman method, and Kappa coefficient

Article information

Inappropriate application: paired t-test, Pearson's correlation

There have been many researchers who reported nonsignificance from a paired t-test or a high correlation coefficient, and mistakenly interpreted the results as evidence of agreement between two corresponding measurements.1 Actually the paired t-test examines if the mean difference between two correlated data could be zero or not: Data with smaller variability may be more likely to get a conclusion of a significant difference by the paired t-test, while data with larger variability and the same mean difference may be less likely to do so. We can easily notice that it is irrelevant because larger variability indicates presence of paired measurements with larger amount of disagreement. Also, the Pearson's correlation coefficient is criticized for generally producing overestimated measures compared to ICC and/or may give totally erroneous results in some specific cases, i.e., when 1 measurement is always 1 mm larger than the other, the correlation is perfect but two measurements never agree. Therefore the paired t-test or the Pearson correlation coefficient should not be used in evaluation of agreement.

Dahlberg error and relative Dahlberg error: quantifying measurement error

The Dahlberg's formula proposed in 1940 provides a method of quantifying measurement error.2 It has been used the most frequently in assessing random errors in cephalometric studies. If we repeatedly measured the inter-canine width of N dental arches by twice, we may use the Dahlberg formula in calculating the size of measurement error. We can get an average squared difference, which is the sum of squared difference between the observed and the (imaginary) true values of the intercanine distances divided by N in either the first or the second measurements. The square-root of the averaged squared difference may be considered as the amount of measurement error, which is the Dahlberg error. However actually we never know the true values, and we may use two repeated measures in calculating the measurement error under assumption that there is no bias.

The variance of the difference between the second measure and the first measure is equal to the sum of variance of errors of the first and the second measures.

The relationship can be expressed as:

Therefore the Dahlberg error, D, is defined as:

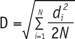
Where d_i is the difference between the first and second measure; N is the sample size which was re-measured.

The Dahlberg error may be obtained by a simple calculation procedure above. Two important merits of the Dahlberg error include that the original unit is preserved and interpretation may be easy because of its similarity to standard error. One shortcoming may be that Dahlberg error does not distinguish between systematic and random errors, by assuming only random errors.

One of the difficulties in interpreting on the size of error is that there is almost no reference for acceptable range because it may depends on various clinical conditions. Frequently many researchers who have reported the Dahlberg error have concluded that "the amount of error was small enough" empirically, without any further explanation. Usually comparative interpretation is difficult when units of measurements are different or when values are quite different. Measurement error of 1 kg may be considered with a fairly different importance when we measure body weight of an infant or when we measure that of an adult. A relative form of Dahlberg error, proportion of Dahlberg error on the average of two comparative measures, may enable direct comparison of error sizes between measurements with different units or between measurements with different means. The relative Dahlberg error (RDE) can be defined as:

RDE may be used to compare size of random errors even among measures with different units.

Bland-Altman method: graphical evaluation of measurement error

The Bland-Altman method provides an intuitive method to evaluate if two methods can be used interchangeably or not.3 The Bland-Altman method is based on visualization of difference of the measurements by two methods using a graphical method to plot the difference against the mean of the measurements.

The Bland-Altman method calculates the mean difference between two methods of measurement and standard deviation (SD) of the difference, and compute '95% limit of agreement' as the mean difference ± 2 SD. The presentation of '95% limit of agreement' on the Bland-Altman plot enables visual judgment of how well two methods of measurement agree. Smaller range between the limit may be interpreted as better agreement. Figure 1 illustrates the Bland-Altman plot.

Figure 1

Illustration of the Bland-Altman plot: Difference against for PEER data.3

Kappa coefficient: agreement for categorical variables

For dichotomous variables which have only two levels, i.e., dead or alive, presence or absence, etc., the Kappa coefficient can be used in evaluation of agreement.4 In a situation that two examiners evaluate whether a patient has an active dental caries or not, intuitively we could think "overall proportion of agreement", simple proportion of same responses in their ratings to assess agreement. However there may be a possibility of agreement only by chance depending on the prevalence of the disease. The Kappa coefficient considers the possible agreement by chance in the equation.4 For example, suppose the prevalence of active dental caries is approximately 20% in 12-year old children. Data of dental caries examination by two examiners may be displayed like Table 1. Overall proportion of agreement, P_o, is simply (15 + 70) / 100 = 0.85. However we would expect that some degree of agreement may be possible only by chance, P_e, even though no association between two examiners was assumed. The expected number is calculated by multiplying marginal numbers and dividing the total number of observation; the top left cell would have (25 × 20) / 100 = 5 expected numbers, and bottom right cell would have (75 × 80) / 100 = 60 expected numbers. Kappa corrects the expected agreement in the formula:

Table 1

Incidence of dental caries rated by two examiners

where P_o is the observed proportion of agreement and P_e is the proportion expected by chance.

In this case, P_e = (5 + 60) / 100 = 0.65 and P_o = (15 + 70) / 100 = 0.85. Therefore, the Kappa coefficient is calculated as κ = (0.85 - 0.65) / (1.0 - 0.65) = 0.571.

The same Kappa coefficient may be obtained using SPSS, following procedure:

Article information Continued