The influence of combining composite resins with different elastic modulus on the stress distribution of Class V restoration: a three-dimensional finite element study

Article information

Abstract

I. INTRODUCTION

Non-carious cervical lesions (NCCLs) are characterized by the loss of dental hard tissue at the cemento-enamel junction (CEJ)1). The etiology and diagnosis of NCCLs remain controversial. Previously, clinicians believed this to be caused solely by toothbrush abrasion, but presently many clinicians now classify this as tooth failure due to occlusal loading2-4). It has been suggested that occlusal loads cause the tooth to flex, particularly during lateral excursion. As the tooth flexes, tensile and shear stresses are generated in the cervical region of the tooth that cause disruption of the bonds between the hydroxyapatite crystals, leading to crack formation and eventual loss of enamel and the underlying dentine5).

Grippo6) proposed a new classification of tooth structure loss called abfraction (from the Latin words ab - away, and fraction - breaking). He defined this as the pathologic loss of tooth substance primarily caused by biomechanical loading forces resulting in flexure and failure of enamel and dentin at a location away from loading.

Clinically, abfraction lesions are wedge-shaped defects that are principally found on the buccal and labial aspects of the teeth. Once the lesion has been formed, the highest stress concentration was observed around the apex of the wedge-shaped lesion7).

NCCLs occur in a variety of forms depending on the type and severity of the etiological factor, but not all lesions require restorations8). The decision to restore NCCLs is based on the desire to strengthen the tooth and decrease the theoretical stress concentration and flexure, mitigate lesion progression, prevent hypersensitivity and pulp involvement, improve oral hygiene and enhance esthetics8,9). Treatment materials have included the restoration with resin-based composites, glass ionomers or a combination of these materials10,11).

Owing to the lack of inherent macromechanical retention in restorations of NCCLs, adhesion is the most important factor in retention of such restorations. However, the retention is affected by various factors such as tooth flexure, occlusal stress, the character of the dentinal surface and elastic modulus of the restorative materials. A clinical study with earlier generation adhesive systems showed that retention of restorations in NCCLs was influenced by the elastic modulus of the composite resin12).

Clinically, composite restorations are appreciated for their esthetic qualities, relative wear resistance, and smooth surface texture. Recently, flowable resin was introduced. Due to the flexibility of this material, it can be used to restore NCCLs. The combination of flowable and microfilled or microhybrid composites combines the advantages of both materials13) and materials combinations may be possible.

According to Park's study14), when restoring the notch-shaped lesion, material with high elastic modulus worked well at the lesion apex and material with low elastic modulus worked well at the cervical cavosurface margin.

The finite element (FE) method has been widely used in biomechanics for evaluating interfacial relationships inside biomaterials or between restoration and tooth surface.

The purpose of this study was to investigate the influence of combining composite resins with different elastic modulus, occlusal loading condition on the stress distribution of the restored notch-shaped NCCL using 3D FE analysis.

II. MATERIALS AND METHODS

1. FE model

To develop a 3D FE model, an intact normal extracted human maxillary second premolar was used. The extracted premolar was scanned serially with Micro-CT (SkyScan1072; SkyScan, Aartselaar, Belgium) to expose the tooth sections perpendicular to the long axis of the tooth (58 µm in thickness) and parallel to the occlusal plane. Image processing software, 3D-DOCTOR (Able Software Co., Lexington, MA, USA), was employed to make the boundaries of enamel, dentin and pulp and to construct a surface model of tooth from the sectioned two dimensional images. ANSYS (Swanson Analysis Systems, Inc., Houston, USA) was used to mesh and analyze 3D FE model.

In this study, the final model consisted of 16,668 elements with 18,245 nodes. A notch-shaped lesion with a 4.28 mm vertical height and a 5.31 mm mesiodistal width was modeled. The modified notch model was the same shaped lesion except for the rounded lesion apex (Figure 1).

Figure 1

3 dimensional finite element model of notch shaped cavity.

The physical properties of the tooth and supporting structures used in this study are given in Table 1. All materials were assumed to be linearly elastic, homogeneous and isotropic.

Table 1

Mechanical properties of the tooth and supporting structures used in the study

The periodontal ligament was assumed to be 0.3 mm wide, and the dimensions of the surrounding compact and cancellous bone were derived from standard texts. Alveolar bone was also generated by growing the outer surface of the tooth model from 2 mm below the CEJ and the cervical cavosurface margin of the cavity15,16). The pulp was modeled as a void since previous researchers17) found that omission of the pulp has no influence on stress profiles. In these models, the outer surface and the base of the alveolar bone model was fixed in order to prevent rigid body motion for FE analysis. The model was also fixed on mesiodistal direction.

2. Restorations

Notch cavities were filled with hybrid, flowable resin and combination of both (Figure 2). The data of material properties such as elastic modulus, Poisson's ratio and polymerization shrinkage were used by literature review18,20,21) (Table 2). The Tetric Flow (Vivadent Ets., FL-9494-Schaan, Liechtenstein) and Z100 (3M Dental Products, St. Paul, MN, USA) were used as representatives of flowable and hybrid resin. The dentin bonding system used in this study was Scotchbond MP (3M Dental Products, St. Paul, MN, USA) and the adhesive layer thickness was 40 µm. The physical properties of the tooth, supporting structures and materials used in this study are given in Table 1. The adhesive layer was made by mathematical shell element modeling and the conjunctions between materials were set as complete coupling.

Figure 2

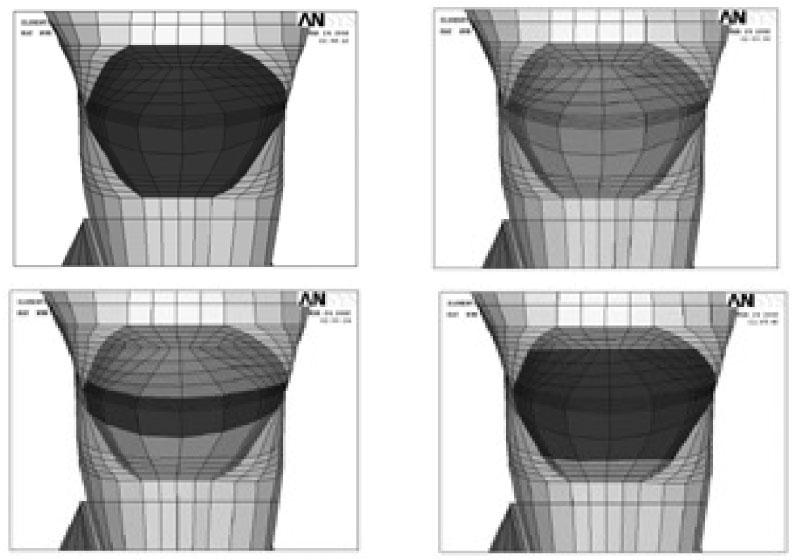
Simulated restorations of notch-shaped NCCL (Upper left; Z100-dark brown, Upper right; Tetric Flow-light brown, Lower left; Combination 1, Lower right; Combination 2).

Table 2

Mechanical properties of the materials used in the study

3. Loading conditions

The model was loaded with two vertical loads of 500 N each, shown in Figure 3. Perpendicular load on the upper third of the palatal slope of the buccal cusp (Load A) and perpendicular load on the upper third of the buccal slope of the palatal cusp (Load B) were used.

Figure 3

Schematic diagram of loading points (A; Perpendicular load on the upper third of the palatal slope of the buccal cusp, B; perpendicular load on the upper third of the buccal slope of the palatal cusp).

4. Experimental groups

The variables were restoration methods (Tetric Flow; T, Z100; Z, Combination 1; C1, Combination 2; C2), and loading conditions (Load A; A or Load B; B).

Combination 1(C1) method was that apex was restored by small amount of Z100 and the occlusal and cervical cavosurface margin by large amount of Tetric Flow. Combination 2 (C2) method was that apex was restored by large amount of Z100 and the occlusal and cervical cavosurface margin by small amount of Tetric Flow (Figure 2).

The tested groups were classified as 8 situations (Table 3).

Table 3

Simulated groups according to cavity designs, restoration methods and loading conditions

6. Node selection for stress analysis

Nodes were selected according to cavity 4 line (occlusal cavosurface margin line, DEJ line, lesion apex line and cervical cavosurface margin line) with 3 areas (mesial, middle, distal) to compare stresses before and after restorations. At the initial pilot study, the highest stress in the unrestored cavity was observed at the mesial point angle (MP). After the cavity was restored with composite resin, the peak stress was moved to more proximal node than MP. Thus, an additional M1 node was selected (Figure 4).

Figure 4

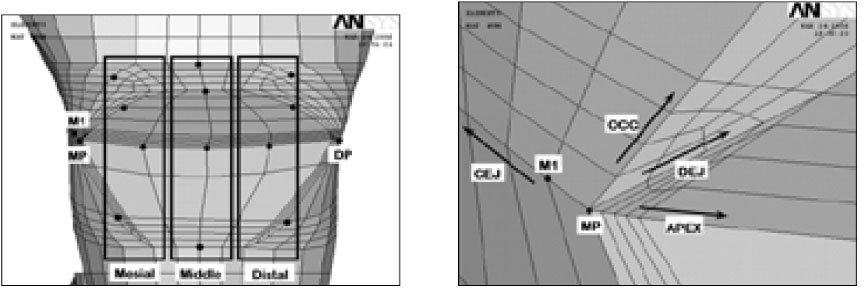
Node selection (left) and magnified aspects (right) of mesial corner of notch-shaped lesion. Along the cavity 4 lines, each 4 nodes were selected at the 3 areas (MP: Mesial point angle, DP: Distal point angle, M1: Nodes near mesial point angle, CEJ: Cemento-enamel junction, Occ: Occlusal cavosurface margin, DEJ: Dentino-enamel junction, Apex: Lesion apex).

7. Comparison with mechanical properties of teeth

The obtained data were compared with the reported mechanical failure range of teeth22) (Table 4).

Table 4

Mechanical failure range of teeth22) (MPa)

III. RESULTS

1. Before restoration

General principal stress distributions before restoration were shown in Figure 5.

Figure 5

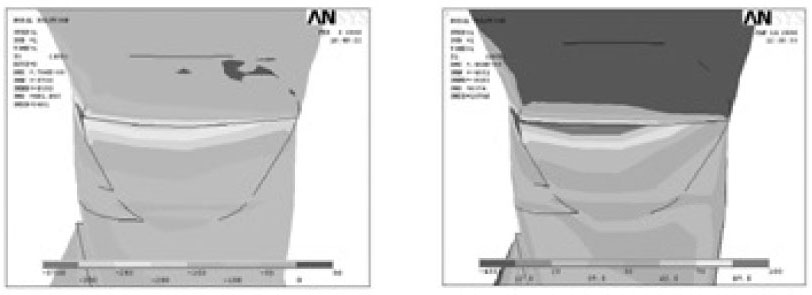
Principal stress distribution of notch-shaped cavity before restoration (Left; Minimum principal stress-Compressive stress, Right; Maximum principal stress-Tensile stress. Upper and lower view's scales were different each other).

The peak compressive stress of 588.0 MPa was concentrated at MP under Load A and the peak tensile stress of 193.3 MPa was concentrated at MP under Load B and these peak stresses were over the stress limit of teeth.

The lesion apex line stresses showed the largest stress value, followed by DEJ line, cervical cavosurface margin line and occlusal cavosurface margin line. Larger apex stresses were observed in the mesial area than in the distal area.

Principal stress distributions of 4 cavity line were shown in Figure 6.

Figure 6

The compressive and tensile stress distribution on occlusal cavosurface margin (Occlusal), DEJ, lesion apex and CEJ (Apex & CEJ), cervical cavosurface margin (Cervical) under Load B (MP: Mesial point angle, DP: Distal point angle, Mes: Mesial node, Mid: Middle node, Dist: Distal node).

2. After restoration

General compressive and tensile stress distributions were shown in Figure 7. After restoration, significant stress relief was shown in the all cavity areas, especially at the lesion apex. However, stress concentration at the mesial corner was still observed as unrestored cavity.

Figure 7

The Principal stress distribution under Load A and B.

Under Load A, stress relief was smaller than other restoration methods when the entire cavity was restored by Tetric Flow (TA) at the lesion apex.

Under Load B, In C2B, stress relief was the largest at the lesion apex and mesial root dentin. Peak stresses were shown in Table 5.

Table 5

Peak stresses of each locations under Load A and B

(1) Occlusal cavosurface margin

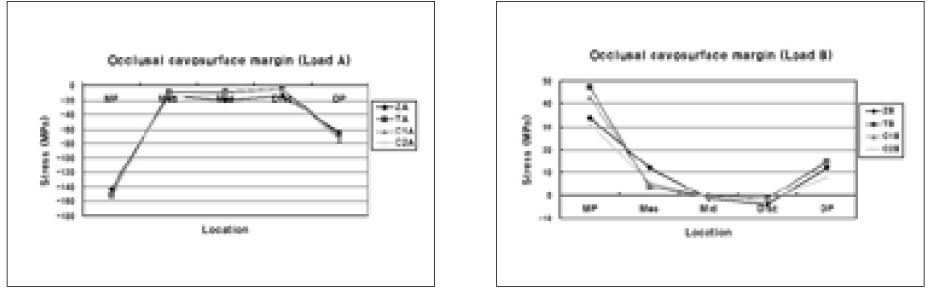
On occlusal cavosurface margin, generally similar compressive stress was seen independently of restorations under Load A (Figure 8). The highest compressive stress of 152.5 MPa was concentrated at MP in C1A under Load A. In ZA, the lowest compressive stress of 142.7 MPa was concentrated at MP. These two stresses were within the limit stress of tooth.

Figure 8

The compressive and tensile stress distribution on occlusal cavosurface margin after restoration under Load B (MP: Mesial point angle, DP: Distal point angle, Mes: Mesial node, Mid: Middle node, Dist: Distal node).

In case of tensile stress, there were a lot of differences of stress value according to restorations at MP. The highest tensile stress of 47.5 MPa was concentrated at MP in TB under Load B. In C2B, the lowest tensile stress of 31.3 MPa was concentrated at MP. As there were a lot of quantities of Tetric Flow (TB, C1B), stresses were developed at MP.

(2) DEJ

On occlusal DEJ, like the occlusal cavosurface margin, similar compressive stress was seen independently of restorations under Load A (Figure 9). The highest and lowest compressive stress value and site under Load A were the same as in the occlusal cavosurface margin.

Figure 9

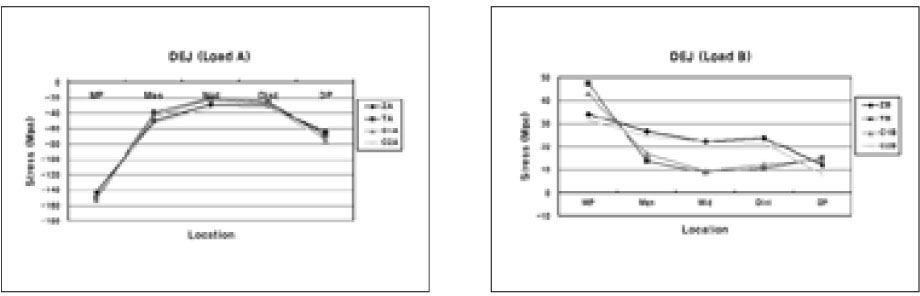
The compressive and tensile stress distribution on occlusal DEJ after restoration under Load B (MP: Mesial point angle, DP: Distal point angle, Mes: Mesial node, Mid: Middle node, Dist: Distal node).

Under Load B, the peak stress value and site were the same as in the occlusal cavosurface margin. However, the stress pattern was different. Two stress reduction patterns were shown. As there was a lot of Tetric Flow (TB, C1B), the peak stress was increased at MP, but stresses were steeply decreased in the middle and distal area.

(3) Lesion apex and CEJ

On the lesion apex and CEJ, similar compressive stresses except peak stress value were observed in all restorations under Load A. The peak stress site shifted from MP to M1 (Figure 10). The highest compressive stress of 291.4 MPa was concentrated at M1 in TA under Load A. In ZA, the lowest compressive stress of 232 MPa was concentrated at M1.

Figure 10

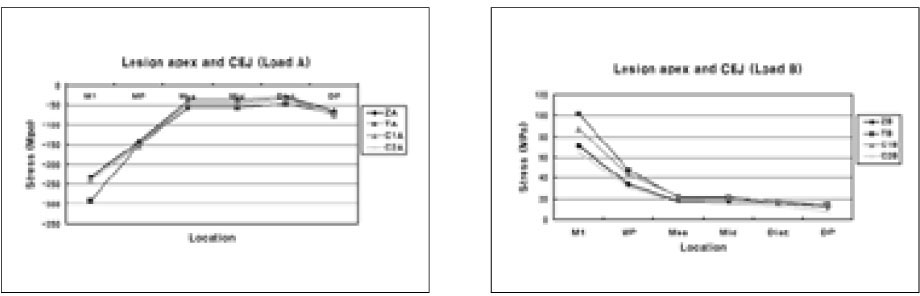
The compressive and tensile stress distribution on lesion apex and CEJ after restoration under Load B (MP: Mesial point angle, DP: Distal point angle, Mes: Mesial node, Mid: Middle node, Dist: Distal node).

Under Load B, the peak stress site also moved from MP to M1. The highest tensile stress of 101.6 MPa was concentrated at M1 in TB. In C2B, the lowest tensile stress of 64.9 MPa was concentrated at M1. In whole lesion apex and CEJ line, the greatest tensile stress relief was observed in C2B.

(4) Cervical cavosurface margin

On cervical cavosurface margin, the highest and lowest compressive stress value and site under Load A were same as at occlusal cavosurface margin. At the middle site, in ZA, compressive stresses were larger than others (Figure 11).

Figure 11

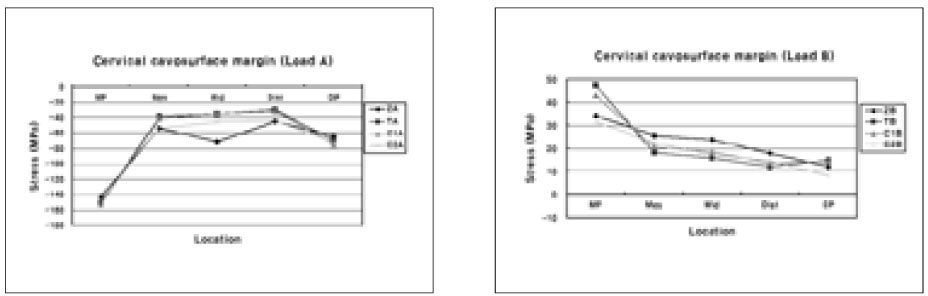
The compressive and tensile stress distribution on cervical cavosurface margin after restoration under Load B (MP: Mesial point angle, DP: Distal point angle, Mes: Mesial node, Mid: Middle node, Dist: Distal node).

Under Load B, the stresses were reduced moving from the MP to DP. Stress declines were all different. The highest tensile stress value and site were same as occlusal cavosurface margin. Similarly, at the lesion apex and CEJ, the best tensile stress relief was observed in C2B.

IV. DISCUSSION

NCCLs vary in size, shape, and most importantly, the cause from which they have resulted. Some clinicians have hypothesized that wedge-shaped noncarious cervical lesions are caused primarily by tooth flexure as a consequence of malocclusion, bruxism, and parafunctional habits2-4).

Once the lesion was formed, the highest stress concentration was observed around the apex of the wedge-shaped lesion7). The discontinuity of the enamel and dentin may cause increased stress and damage in the enamel23). The severity of geometric discontinuity of NCCL can be expected to have strong influence on the development of internal stress in teeth24). In our experiment, the stresses converged in the apex line with more mesial side under both loading conditions. These asymmetric patterns of mesial stress distribution were related to the anatomical asymmetry of the teeth.

When clinically assessing NCCLs, dental practitioners must consider if the cervical defect requires a restoration and if so, which restorative material will provide the best outcome. Additionally, the clinician must consider a modulus of elasticity, resistance to wear and ability to withstand acid dissolution9,25). A number of researchers have reported controversies regarding restoration of class V cervical lesions8,10,11). Recently resin composites with dentin bonding agents have become a popular for the restoration of NCCLs26). In the current experiment, lesions were restored by conventional hybrid resin and flowable resin.

Important factor affecting retention failure is the elastic modulus of the restorative materials. It has been demonstrated that a strong correlation exists between marginal failure and Young's modulus of the composite restoration material in the class V situation27). It is a general rule of engineering that stress will always follow the path of the stiffest material, that is, the path with the highest elastic modulus. In the case of an intact tooth, the stiffest material is the enamel, and an applied occlusal load is generally passed through the enamel and into the underlying dentine, with the load being dissipated through the crown and down into the root in a radial and apical direction28).

Therefore, strictly from a mechanical point of view, it can be said that the best approach is to apply restorative materials with high Young's modulus as possible. Yaman et al.29) concluded that for class V applications Z 100 gives the most promising results. According to Nakayama et al.30) a Young's modulus equal to or greater than that of the dentine is required for resin composite to resist deformation by occlusal stress. In addition, resin composite Z 100 has a high Young's modulus and a high percentage of volume fraction filler, which increases resistance to deformation by occlusal force31). When using a hard material, the stiffest restoration-tooth interface resulted in the lowest restoration displacement.

In contrast, some researchers contend that one of the methods used to maximize the retention rates of class V restorations is the placement of low elastic modulus materials. Heymann and colleagues32) reported that the retention rates for restorations of a material with lower elastic modulus were significantly higher than those of a material with higher elastic modulus. The rationale behind this is that high modulus materials are unable to flex when the tooth structure is deformed under load and therefore they are displaced from the cavity. In contrast, low modulus materials can flex with the tooth and therefore can remain in situ. Thus, these resins will absorb much of the masticatory stresses rather than transferring it to the dentin-restoration interface11). A low elastic modulus also contributes to stress relief from polymerization shrinkage of composites, preserving the marginal integrity of restorations33). This property allows for good wetting along the cavity walls, which improves the adaptation of the restorative material.

In the current study, two different elastic modulus materials were used. The stress values after restoration were different at the 4 lines depending on the elastic modulus of the materials. The highest stress reduction was observed at the apex in the Z100 restoration which had the higher elastic modulus. In the other 3 lines, especially at the cervical cavosurface margin, Tetric Flow restoration showed a smaller stress value compared with Z100. Therefore, the combination of flowable and conventional hybrid composites may offer a synergistic effect of both materials. It was hypothesized that Z100 composites used as a strut would improve the reduction rates of stress in the apex. This hypothesis was based on earlier studies29) showing that restoration using Z100 worked as a strut to prevent stress concentration of the lesion.

Under Load A, similar compressive stress was observed independently of kind of combination restorations. However, under Load B, different stress values appeared. As there was a lot of Tetric Flow, stresses were greater at the apex, but stresses were smaller at the other 3 lines. Z100 was reversed. These results show that high elastic modulus materials work well at the lesion apex. This is also involved with special feature of notch-shaped cavity. Due to its sharpest geometrical discontinuity, stress was focused on the lesion apex in the notch-shaped cavity. When biting force is applied, a high elastic modulus material like as a strut can sustain the stress at the apex. This is especially true under Load B when tensile stress occurs.

In this experiment, C2 method was the best method for tensile stress reduction. The cavity apex was restored by a combination method such that apex was restored by Z100 and the occlusal and cervical cavosurface margin by small amount of Tetric Flow. Thus, this method is recommended for restoration of notch-shaped lesion because it showed the best effect in tensile stress.

Experimental in vitro dental stress studies of abfraction generally have employed two methods: photoelastic stress models and FE analysis. In the present study, a 3D FE method has been used to calculate the stress field in directly paced class V composite restorations. A direct, quantitative comparison between the stresses generated by these techniques has been made. Two-dimensional axisymmetric finite element modeling has been used in most previous research22,23,28). Although numerical results can be easily obtained in two dimensional modeling, it has some significant shortcomings. Because the shape of a human tooth is highly irregular, it can not be represented in a two-dimensional space and the actual loading can not be simulated without taking three dimensions into consideration. Therefore, three-dimensional modeling with the actual dimension is preferred for a reliable analysis.

The result of this study must be interpreted with a certain amount of caution. First, it was hard to include all factors that occur intraorally in this computer simulation. Therefore, some simplification was used. Second, this study compared finite element models assuming one to have an isotropic enamel and dentin, but the real tooth model was an anisotropic enamel and dentin model. Third, these static load stresses may not reflect the actual conditions encountered intraorally, therefore may not adequately describe the functional movement of occlusion.

Further research is needed to assess the mechanism through which noncarious cervical lesions are initiated and propagated, as well as the potential role of abfraction. Such investigations will include intervention studies with occlusal therapy to investigate whether eliminating occlusal loading factors prevents formation, progression of cervical lesions and loss of restorative material. Our future investigations will also include studies of other restoration methods as well as optimal materials of stress induced cervical lesions.

V. CONCLUSIONS

Within the limitations of this study, it is concluded that when restoring notch-shaped NCCL, combining method such that apex was restored by material with high elastic modulus and the occlusal and cervical cavosurface margin by small amount of material with low elastic modulus was the most profitable method in the view of tensile stress that was considered as the dominant factor jeopardizing the restoration durability and promoting the lesion progression.

Article information Continued